简支与连续梁桥在汽车制动作用下的冲击系数对比研究

王 芳，赵 伟，刘雅婷

(宿州学院资源与土木工程学院，安徽 宿州 234000)

0 引言

车辆在桥上行驶时与桥梁间产生的相互影响的振动作用，称为车桥耦合振动[1]。桥梁在车辆荷载作用下动力效应的增大值用动力冲击系数(IM)来表征。我国桥梁设计通用规范(JTG D60—2015)[2]规定以桥梁基频计算冲击系数；对于连续梁桥，分别采用桥梁的一阶频率和二阶频率作为计算冲击力引起的正、负弯矩效应。然而已有不少研究发现，仅考虑桥梁基频计算的冲击系数可能会低于桥梁实际动力响应产生的冲击系数，不利于桥梁的设计和安全评估[3-4]。

冲击系数受诸多因素的影响，具有明显的不确定性。国内外学者针对车桥耦合振动开展了大量的研究，得到很多重要的结论，但大多数局限于匀速运动[5-7]。然而实际交通中，车辆超车或遇到紧急情况经常会做变速运动，产生的IM很可能会超过规范规定数值[8]。因此变速情况下的车-桥耦合振动研究是很有必要的。彭献[9](2006)、方志等[10](2008)将汽车荷载简化为单个集中荷载或简化的平面车辆模型，将桥梁简化为简支梁进行了汽车变速行驶时车-桥耦合振动中的研究。多跨连续梁桥的跨度大、整体稳定性强，在实际工程中得到广泛应用。Law等[11]、陈榕峰等[12]研究了考虑变速情况的三跨连续梁桥和单跨简支梁桥的动力响应，发现同等条件下，连续梁桥IM的变化规律与简支梁桥不一定相同;陈水生等[13]研究了曲线连续梁桥在不同工况下车辆制动作用时的动力响应情况。

为了比较简支与连续梁桥在汽车制动作用下的动力冲击系数，本文基于三维车桥耦合振动程序，计算了4座不同截面和跨径的混凝土梁桥，包括2座简支和2座连续梁桥，在一辆三轴车制动作用下的IM。考虑的工况包括：3种减速度(a)、6个不同初速度(v)、7个不同的刹车位置(P)、3种不同等级的路面不平整度水平(RSC)。对单跨简支梁桥和三跨连续梁桥的IM结果进行了比较，并将计算结果与我国现行规范规定的值进行了对比。

1 车-桥耦合振动分析模型的建立

1.1 车辆模型

本文选用的三维整车模型(HS20-44)来自美国公路桥梁标准规范设计用车[14]。该车共11个自由度，总质量32.63 t，车辆模型示意如图1所示。

图1 三轴车模型

1.2 桥梁模型

本文共选用4座混凝土梁桥，其中简支梁桥跨径为30 m，连续梁桥跨70 m(20 m+30 m+20 m)，截面类型分别为T梁桥和箱梁桥。桥梁模型具体信息如表1所示，截面形式如图2所示，车辆加载位置均为车道2正中。

1.3 桥面不平整度

在影响车桥耦合的因素中，桥面不平整度(road roughness condition，RSC)为主要激励源。国际标准化组织(ISO)[15]将桥面不平整度划分为5个等级，

表1 4座桥的基本参数

图2 桥的横截面及车辆加载位置

具体如表2所示，本文采用其中“好” “中” “差”3种等级。同时，为消除桥面不平整度生成过程的随机性对计算结果的影响，每种工况生成20个随机桥面，最终的动力冲击系数IM是这20次运算结果的平均值。

表2 桥面不平整度等级

2 车-桥耦合系统运动方程求解及IM计算

2.1 车-桥耦合系统运动方程及其求解

当车辆在桥上匀速通过时，车-桥耦合系统运动方程是利用车辆在桥上行驶时车轮与桥面接触点处的位移和接触力关系建立起来的，具体如式(1)所示：

(1)

式中：M、C、K分别为质量、阻尼、刚度矩阵；{d}为位移向量；下标b代表桥梁，v代表车辆,r代表车体；F为力，其中，FG为车辆重力；Cb-b、Cb-v、Cv-b、Kb-b、Kb-v、Kv-b和Fb-r是由车-桥相互作用力引起的随时间变化的量。

桥梁的位移响应{db}求解得到后，与单元应变矩阵[B]相乘即可得到应变{ε}。

2.2 IM计算

冲击系数(IM)是在桥梁设计中用来表征车辆过桥时对桥梁的冲击效应的系数，表达式为：

(2)

式中：ysmax和ydmax分别为桥梁在车辆荷载经过时产生的最大静响应和最大动响应，在具体计算时可采用位移、应变和支座反力等得到，本文采用应变冲击系数。

本文中的两座简支梁桥IM采用的是桥跨中处的正弯矩进行计算；连续梁桥选取是第一跨和第二跨跨中处的正弯矩和第一跨支座处的负弯矩的动力响应进行IM的计算。

2.3 车辆变速情况的考虑

当桥上的车辆变速时，以车辆制动为例，车辆紧急制动产生的惯性力FI(F1=-ma)与车轮处的摩擦力将形成一对仰俯力矩，以M=FIhv来表示，其中m为车辆质量，a为车辆水平加速度，hv为车辆质心距地面高度。

3 参数分析

本文的研究工况包括：(1)3种不同等级的路面不平整度水平RSC，即：“好”“中” “差”；(2)6个不同初速度v，分别为30、45、60、80、100、120 km/h；(3)3种减速度a，分别为-2、-4、-6 ms-2；(4)7个不同的车辆制动位置P，分别为L/8、L/4、3L/8、L/2、5L/8、3L/4、L7/8，以车前轮位置为依据。

3.1 初速度及粗糙度的影响

取车辆加速度取为-6 ms-2，车辆制动位置取“3L/8”，计算了简支梁桥T30连续梁桥T70在3种RSC下的冲击系数。IM计算结果随车辆初速度变化的情况如图3所示，其中虚线为车辆匀速行驶情况的计算结果，实线为车辆加速度为-6 ms-2时的计算结果。

从图3中可以看出：(1)IM数值随着路面不平整度变差而明显增大；(2)车辆匀速行驶和制动情况下获得的IM随初速度的变化均没有单调的递增或递减关系，其中，当车辆以初速度30 km/h过T20桥时，IM大于以其他初速度行驶时产生的结果；(3)车辆在速度30 km/h制动时，连续梁桥T70的IM小于同工况时的匀速行驶IM值，这是由于车辆在此速度时制动将停在桥上的原因。箱梁桥B30和B70有类似的结果。

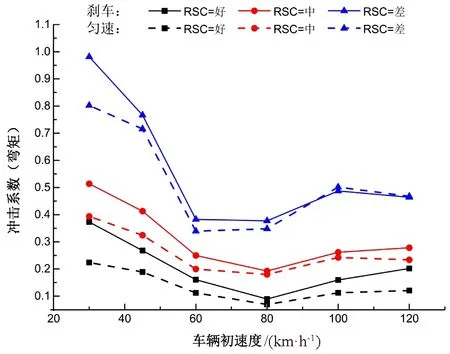
a.T30在不同初速度及粗糙度下的动力冲击系数

b.T70在不同初速度及粗糙度下的动力冲击系数

3.2 汽车制动位置及减速度的影响

当路面不平整度等级为“好”、初速度120 km/h时，本文中的4座桥在3个不同减速度及7个不同位置处制动时的IM如图4所示。2座简支梁桥取跨中的冲击系数，连续梁桥取第2跨跨中的冲击系数，每种工况下的匀速计算结果也包含在图4中。

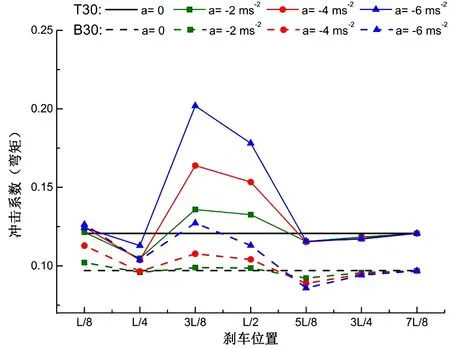
a.T30、B30在不同减速度与刹车位置下的冲击系数

b.T70、B70在不同减速度与刹车位置下的冲击系数

从图4可以看出：(1)车辆制动对应的冲击系数明显大于同工况下的匀速计算结果，且减速度绝对值越大，IM随之增大；(2)T30、B30与T70、B70在相同的减速度下的IM数值都是汽车在桥前半跨制动产生的值大于后半跨制动，且随制动位置变化的趋势基本相同；(3)2座连续梁桥在“L5/8”之前刹车IM均增大，在“L5/8”之后刹车则第二跨跨中的IM不再变化，其中在“L/4”～“5L/8”产生的IM最大。这说明对于连续梁桥，某一跨的动力响应不仅会受到汽车在此跨制动时的影响，汽车在进入此跨之前制动都可能对该跨的动力响应产生影响。因此，对于汽车制动时连续梁桥的冲击系数有必要分跨分别考虑。

3.3 简支与连续梁桥汽车制动情况对比

为对比分析汽车制动情况下简支与连续梁桥动力响应的异同，本文中的4座梁桥在不同工况下的IM结果如表3所示。其中车辆匀速行驶情况IM取自6个速度下的平均值，汽车制动时的IM取的是与匀速情况相同的6个初速度在3个减速度及4个不同刹车位置处产生的最大值的平均值。同时，用我国规范给出的公式计算的IM值也列于表3中进行对比。

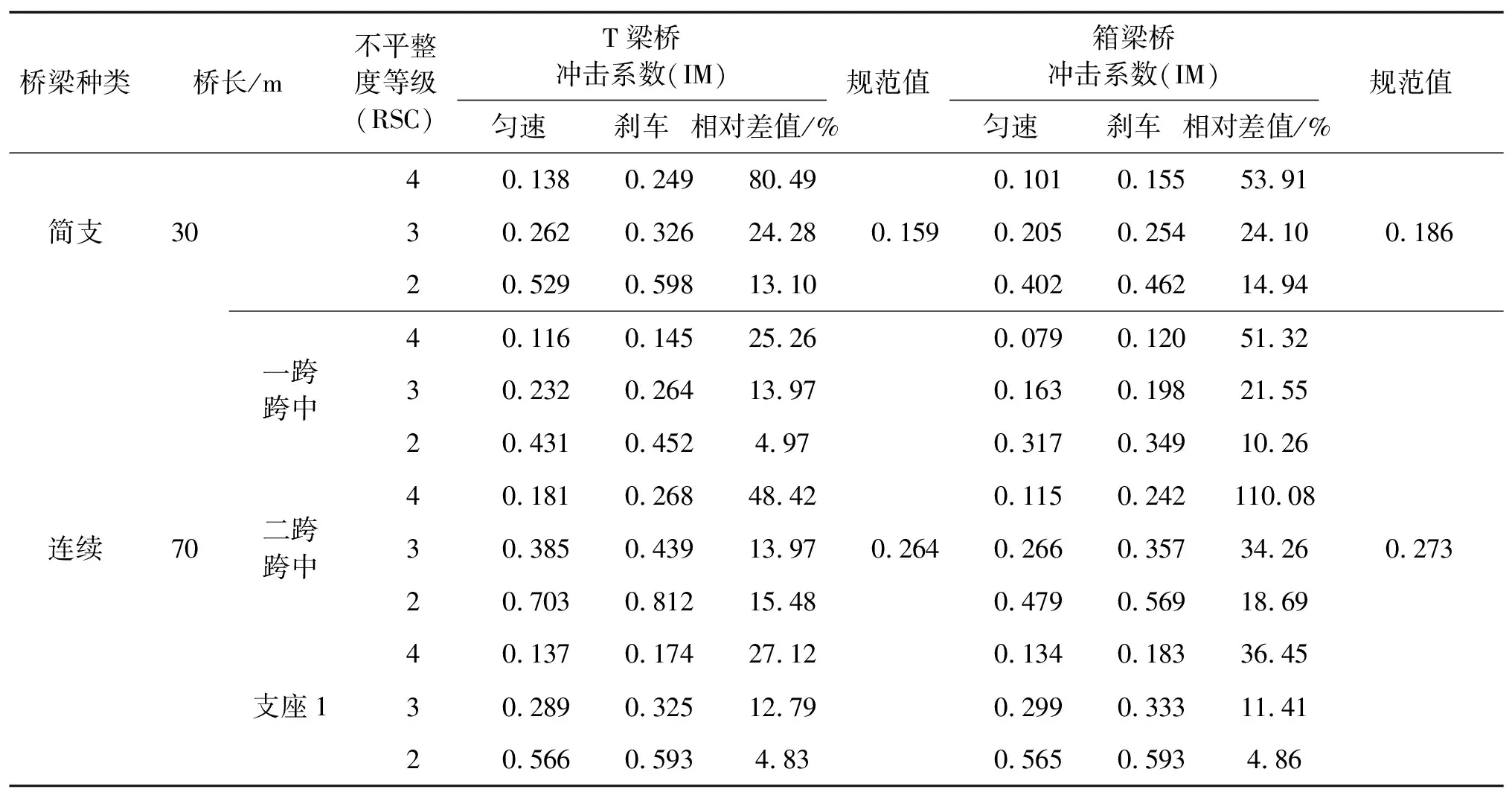
表3 汽车制动下不同梁桥的IM对比

从表3可以看出，总体而言：(1)汽车匀速与制动情况下，跨径为30 m的简支梁桥，T梁桥的IM大于箱型梁桥；跨径相同的简支梁桥，一般情况下T梁桥对汽车制动更“敏感”(跨径为30 m、不平等度等级为“2”时除外)；(2)对于连续梁桥，匀速时，T梁桥的冲击系数基本大于箱型梁桥，但刹车时支座处的IM小于箱梁桥；T梁桥的冲击系数对刹车的敏感度小于箱型梁桥。说明同种工况下，同跨径截面形式不同的梁桥的IM的大小关系不一定相同，汽车制动对IM数值大小的影响程度也不一定相同；汽车制动时连续梁桥不同位置处的IM在的变化规律不一定相同，因此有必要分别考虑；(3)当路面不平整度为“差”和“中”时，匀速与制动时的IM值分别全部和有一半超过规范规定值；当路面粗糙度为“好”时，匀速结果均满足规范值，但汽车制动时的IM值出现了大于规范规定值的情况。因此在实际交通运营中，注意桥梁路面的养护和维修对于减小车辆对桥梁的冲击效应具有很重要的意义。同时，在规范中纳入汽车制动对冲击系数的影响是很有必要的。

4 结论

本文基于车桥模型分别计算了汽车匀速行驶与制动情况下简支与连续梁桥的冲击系数，并且分析了不同路面不平整度水平、初速度、刹车位置、减速度等因素对IM的影响规律。对2座简支梁桥与2座连续梁桥在同工况下的IM结果进行了对比，同时将计算的IM值与我国规范规定值进行了比较。得出的主要结论如下。

1)路面不平整度和汽车制动对桥梁的冲击系数影响显著，平整度越差、减速度绝对值越大，产生的IM值越大；当路面不平整度水平为“差”时，多种工况下的IM值均超过我国规范值。

2)汽车制动时，其他条件相同时，连续梁桥不同位置处的IM的变化规律不一定相同，且汽车在进入某一跨之前刹车都会对此跨的动力响应产生影响。因此，对于汽车制动时连续梁桥的IM有必要分跨分别考虑。