基于稀疏贝叶斯算法的演化博弈网络重构
2022-05-05赵丽娜张亚楠肖玉柱
赵丽娜,张亚楠,肖玉柱
(长安大学理学院,陕西 西安 710064)
0 引 言
网络重构是复杂网络系统研究中的逆问题,即根据大量系统观测数据,如依据个体的时间演变状态等个体信息,去推断节点之间的相互作用关系,从而获得整个网络的拓扑结构。复杂网络重构的研究涉及了数学、计算机科学、社会学、生物学等不同领域的学科[1-4],典型的例子包括重构社会人际关系网络、基因调控网络、金融机构之间的借贷网络、计算机网络等[5-7]。随着网络科学研究的深入,科学界越来越认识到网络结构对网络的行为起着重要作用。然而,实际中的网络结构往往是未知的,因此基于数据的复杂网络的重建问题引起了持续关注。学者们已经发展了一些基于统计物理、信息论和逆向工程的网络重构方法,如Wang等人[8]利用压缩感知理论重构了复杂耦合振子网络;Mantegna[9]利用相关性和互信息的方法获得了股票之间的层级结构信息;Luo等人[10]利用Granger因果关系重构了基因网络等。
演化博弈是自然和社会系统中一种常见的互动类型,探知演化博弈网络的拓扑结构是理解其功能和集体行为的基础[11]。对于演化博弈网络,个体的博弈行为通常难以用动力学方程进行描述,而且相关的时序信息一般数量有限并且是离散的。因此,如何基于少量离散的个体博弈时序信息,挖掘出潜在的节点间连接关系并重构成网络具有重要意义。基于压缩感知的复杂网络重构方法已经被用来求解演化博弈网络重构问题,该方法能够以相对于网络规模很少量的数据实现网络连接的重构[5]。压缩感知重构算法[12]主要有2类:一类是用凸优化模型求解[13],这类重构算法所需要的测量数据少但计算复杂度较高;另一类是用贪婪算法进行求解[14],此类算法计算速度快,但是精度低。此外,这2类算法都不能在噪声较大的情况下获得好的重构效果。
稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)算法作为一种基于概率统计的稀疏重构方法,给稀疏信号处理提供了新的求解思路[15]。该算法考虑了因测量系统误差或加性噪声带来的不确定性影响,已经被广泛应用于医学成像[16-17]、地震探查[18]、信号的无线传输[19]等领域,并取得了优于传统方法的求解结果。本文尝试将SBL重构算法应用于演化博弈网络的重构,解决传统压缩感知重构算法复杂度高以及对噪声鲁棒性差的问题。研究表明在典型的雪堆博弈[20]和囚徒博弈[21]中,即使每个博弈个体的策略和收益的可用信息有限,该方法也能够以更快速的方式识别节点间的连接情况,并且在有噪声的情况下具有更好的重构性能。
1 博弈网络重构算法
1.1 博弈模型
在囚徒困境博弈(PDG)和雪堆博弈(SG)中,假设博弈个体两两进行博弈,任何时候一个博弈方可以选择2种策略(S)中的一种:合作(C)或背叛(D)。当博弈个体选择合作时策略可以表示为向量S(C)=(1,0)T,选择背叛时策略可表示为向量S(D)=(0,1)T。博弈中2个博弈方的收益由他们的策略和给定博弈收益矩阵决定。对于PDG和SG,收益矩阵分别为:
(1)
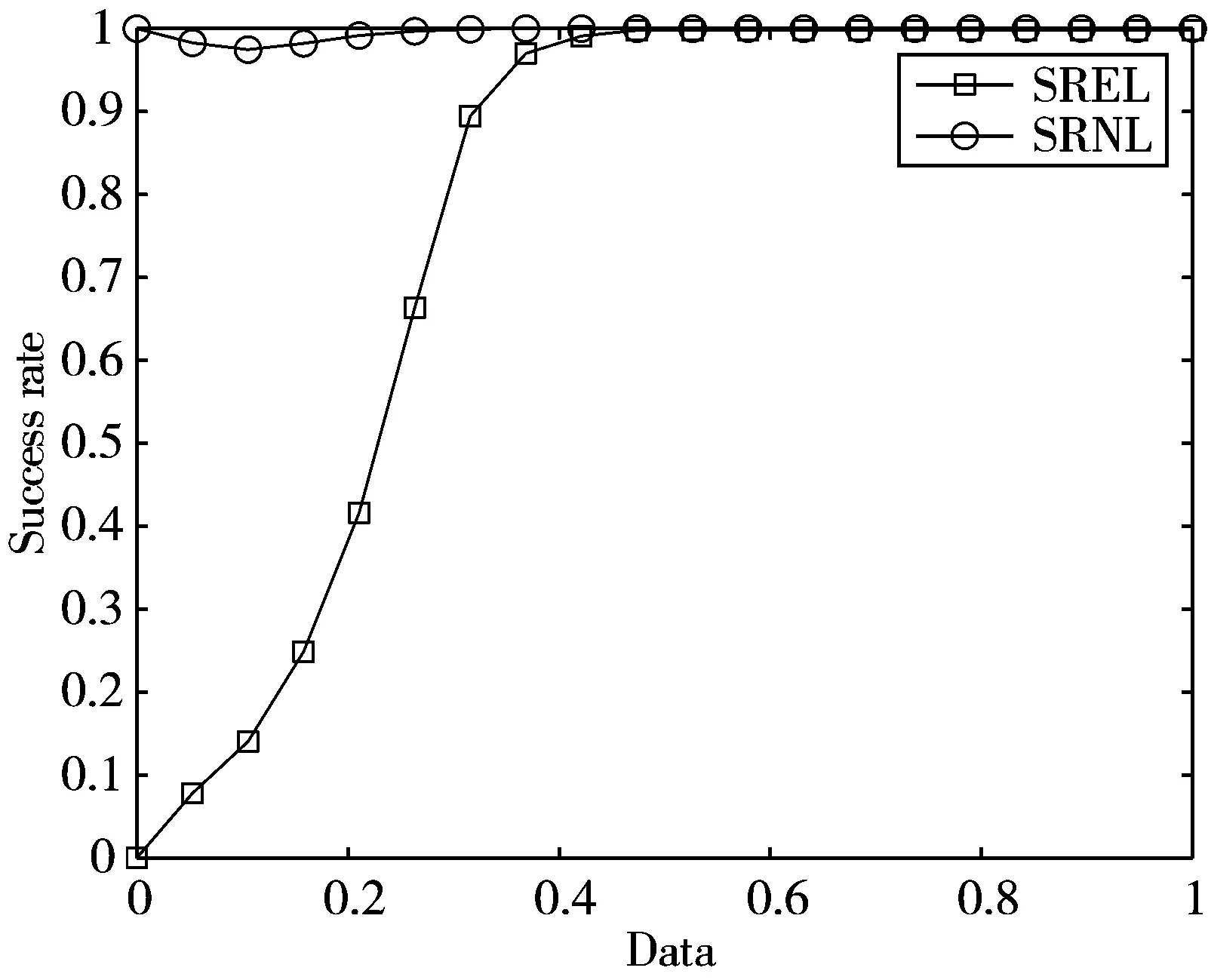
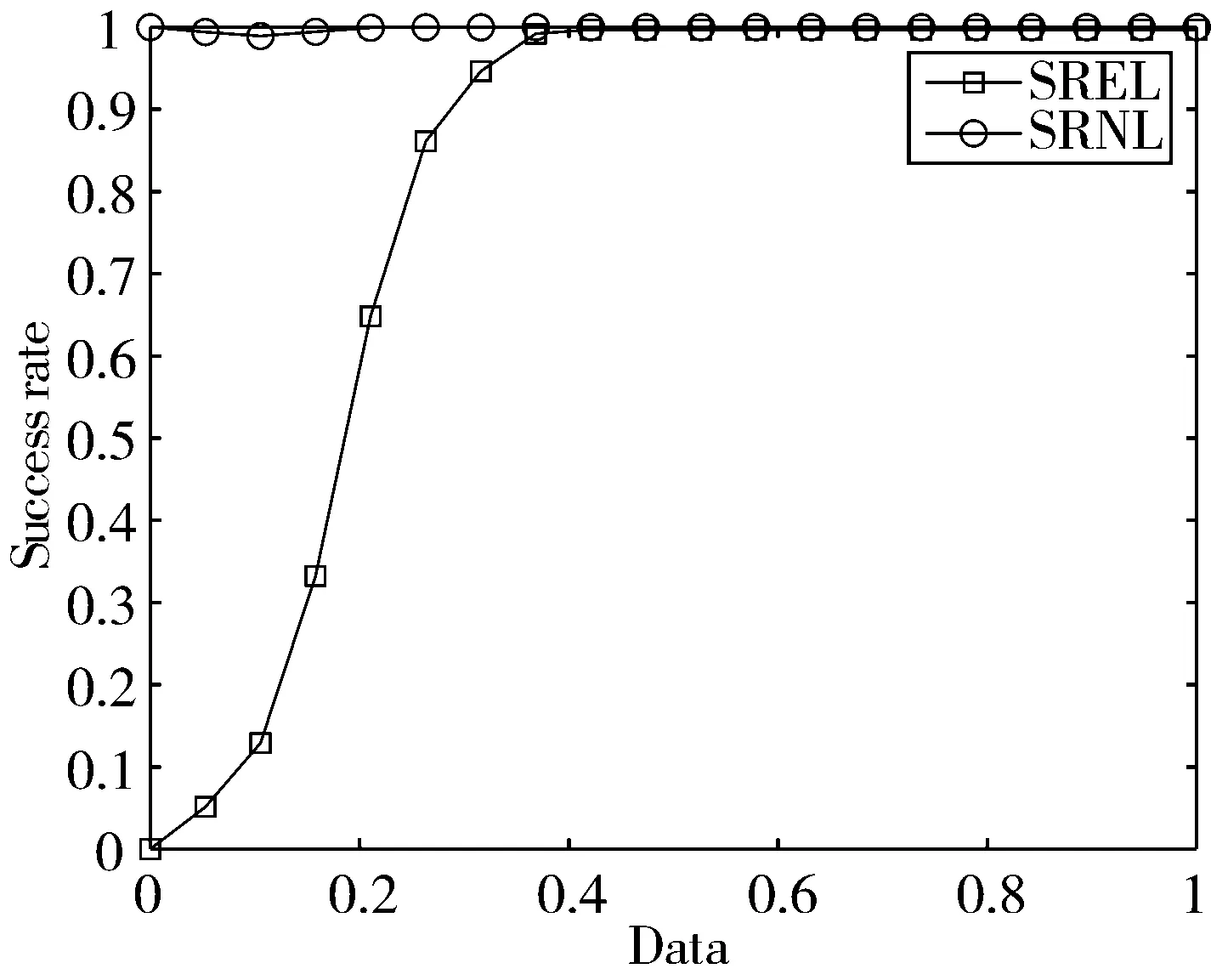
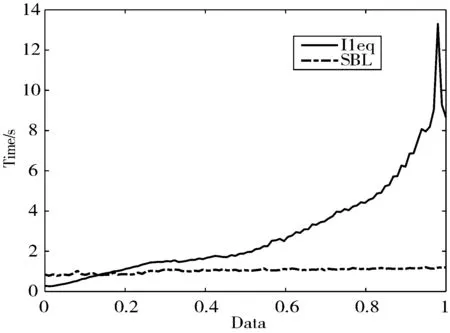
其中,b(1 (2) 其中,Si和Sj分别表示博弈个体i和j的策略,Γi表示个体i的所有邻居的集合。获得收益后,所有个体会根据其自身和邻居的收益更新博弈策略,试图在下一回合获得最大收益。在演化博弈动力学研究中常使用费米规则[22]作为更新策略,即个体i在下一回合学习个体j的策略的概率为: (3) 其中,参数κ>0为噪音,表示博弈动力学中的随机不确定性,一般是一个很小的值,常取0.1。κ=0意味着博弈个体是绝对理性的,即当邻居j的收益大于自己时,个体i以概率1采取个体j的策略作为自己下一轮的策略;当邻居j的收益小于自己的收益时,个体i以概率0采取个体j的策略作为自己下一轮的策略,即在下一轮的博弈中仍然保持自己当前的策略。κ→∞代表参与者完全随机决策。 博弈网络重构问题的关键在于建立个体收益和策略之间的关系。假设博弈网络的节点数为N,节点之间的连接情况可以用一个N×N的邻接矩阵A来表示。如果个体i和j是进行博弈的邻居节点,那么邻接矩阵A的元素aij=1,否则aij=0。根据式(2)可得博弈个体x在t时刻(回合)的收益为: (4) Gx=Φx·Ax (5) 其中,Ax=(ax,1,…,ax,x-1,ax,x+1,…,ax,N)T描述个体x与网络的其他节点的连接情况,Φx为m×(N-1)维矩阵: (6) 通过求解式(5)可以获得向量Ax,从而可以获得x与其他节点的连接情况。以类似的方式可获得其他节点的连接情况,最终完成整个网络结构的重构。由于实际中多数网络的连接是稀疏的,即Ax中的大部分元素为0,因此可以在m 压缩感知是近年来提出的一种数据获取和信息采集方式,通过挖掘信号内在的稀疏特征,从远小于信号维度的压缩数据中重构原信号[23]。即通过少量测量y∈RM恢复信号x∈RN并满足: y=Φx (7) 其中,Φ为M×N的观测矩阵。当方程个数远少于未知数个数(M≪N)时,式(7)是欠定的,因此方程组没有唯一解,无法实现信号重构。如果加上稀疏约束,则信号重构问题可以表示为: min‖x‖0s.t.y=Φx (8) 其中,L0范数‖x‖0表示x中非零元素的个数。由于对式(8)直接求解是NP问题,常见的求解思路是使用L1范数替代L0范数,即求解凸优化问题: min‖x‖1s.t.y=Φx (9) 稀疏贝叶斯学习(SBL)方法最初作为一种机器学习算法,后被引入稀疏信号的重构[25]。SBL重构算法的总体目标是从以下数学模型中估计稀疏信号x: y=Φx+ω (10) 其中,ω为噪声。假定x中的每个分量相互独立且服从均值为0、方差为γi的高斯分布,即: (11) 其中,xi(i=1,…,N)表示x中的第i个分量,γi是未知参数,由算法自动估计出来。在SBL的框架中,假设噪声服从均值为0、方差为δ2I的高斯分布,即: p(ω|δ2)=N(0,δ2I) (12) 根据以上假设可以得到y的后验分布为: (13) 由全概率公式可得观测变量y的边缘概率密度函数为: (14) 其中,Σy=δ2I+ΦΓΦT,Γ≜diag(γ)。利用贝叶斯基本定理可得到x的后验分布: p(x|y,γ,δ2)=N(μ,Σx) (15) 其中,μ=(δ2)-1ΣxΦTy,Σx=((δ2)-1ΦTΦ+Γ-1)-1。通过EM算法估计参数γ和δ2,参数γ在第k次的迭代估计为: (16) 参数δ2在第k次的迭代估计为: (17) 与广泛使用的基于L1的优化算法相比,SBL算法具有以下优势:1)SBL算法在优化求解过程中自动保证了x的稀疏性而无需人为设置参数,且算法复杂度低,收敛速度快;2)基于SBL重构算法在建模中考虑了对噪声影响,因而相对非贝叶斯算法具有较好的抗噪性能。因此,本文将尝试应用SBL算法研究博弈网络的重构问题,进一步提高重构算法的收敛速度,以及对噪声的鲁棒性。 本章将采用MATLAB实验平台,以随机网络[26]和小世界网络[27]为例对本文基于SBL的重构方法进行模拟验证,并和基于l1-magic软件包的重构结果从以下3方面进行比较:1)重构所需数据量;2)算法的收敛性能;3)算法对噪声的鲁棒性。为了量化重构方法的重构性能,引入存在链接重构成功率(SREL)和不存在链接重构成功率(SRNL)。对于给定的节点,SREL定义为成功预测的邻居数与实际邻居数的比值,SRNL定义为成功预测的非邻居数与实际的非邻居数的比值,整个网络的SREL和SRNL由网络所有节点SREL和SRNL的平均值定义。将存在和不存在链接分开处理的原因在于复杂网络的稀疏性,即不存在链接的数量通常比存在链接的数量大得多。由于在实际求解中,邻接矩阵A中的元素不可能精确等于1或0,因此,在实验中指定一个较小的阈值0.1,这样存在链接的范围为1±0.1,不存在链接的范围是0±0.1,这2个区间之外的任何值都被认为是预测失败。 给定网格节点数N=100,网络中任意2点以概率p=0.1相连接(2个参数共同反映了网络的疏密程度,本实验中参数的取值保证了网络的稀疏性)。有研究表明,随机网络模型与现实世界有很大相关性,例如社交媒体平台形成的网络结构特征类似于随机网络。因此,研究随机网络有助于人们理解小型社交网络的结构。2种博弈类型在随机网络的重构成功率如图1和图2所示。PDG和SG的收益矩阵中的参数分别为b=1.2和r=0.7(在参数的取值范围内测试了其他数值,取得了类似的成功率),噪声参数κ=0.1。Data表示测量值的数量与网络节点数N的比值。Success rate表示存在/不存在链接预测的成功率。对于不同的博弈类型,只要极少量的数据就可以获得完美的成功率。例如,对于囚徒困境博弈,实现100%成功率所需的数据长度在0.4左右。从图1和图2可以看出SBL求解方法和L1算法在成功重构网络时所需的最小数据量是相近的。L1算法和SBL算法成功重构囚徒博弈网络所需的最小数据量分别为0.40和0.44;重构雪堆博弈网络所需最小数据量分别为0.39和0.46。 (a) L1重构 (a) L1重构 为了进一步测试本文算法的求解速度,与L1算法进行收敛性能的比较。采用囚徒博弈数据在节点数为N=100的随机网络上进行实验(见图3)。从算法收敛时间可以看出,SBL算法的收敛速度要优于L1优化算法,尤其是在数据量比较充足的情况下,可以进行更高效的求解。 图3 随机网络中算法收敛时间比较 在现实生活中,噪声是无处不在的,很难得到没有噪声的数据集。因此,在观测数据受噪声污染的情况下测试了2种重构算法的抗噪性能。实验中,参数设置与本文第1个实验中重构PDG网络参数设置相同。在PDG的收益数据中分别加入不同信噪比(Signal to Noise Ratio, SNR)的高斯白噪声,图4~图6给出了2种算法在SNR分别为10 dB、5 dB和1 dB的重构情况(在不同信噪比仿真实验中,过小的噪声对2种算法的重构效果影响不大,而很大的噪声则使得2种算法均不能完全重构,因此选取了噪声由小到大的3组有代表性的结果,在大量的仿真实验均表明了以下的结论)。实验表明,在噪声大小和观测数据量相同时,SBL可以获得更高的重构精度。例如SNR=5 dB时,使用0.4的数据量进行重构,SBL算法求解的存在链接预测成功率为0.9左右,而L1算法仅为0.65左右。另一方面,随着噪声的增大,二者重构效果逐渐变差,但SBL重构方法依旧可以在数据量相对充足的情况下进行重构。综合可以看出在噪声环境中,SBL重构方法具有更好的稳健性。 (a) L1重构 (a) L1重构 (a) L1重构 小世界网络最早是由Watts等人[27]在1998年引进的一种断边重连的构造网络的方法。从规则网络入手,随机以某个概率p断掉规则网络的边并且随机选择网络中的顶点进行重连。小世界网络是一种既具有较高的集聚又具有很短的平均最短路径的网络结构。它连通了规则和完全随机2个极端的性质,能够更好地刻画实际网络的结构性质。一些研究表明,生物学、物理学、社会学中大多数网络都具有小世界网络的特征[28-29],因此研究小世界网络具有广泛的现实意义。 本文中以节点数N=100,每个节点的连接边数k=8(该参数反映了网络的疏密程度),重新连接概率p=0.1(当重连概率较小时,网络既具有较短的平均路径长度又具有较高的聚集系数,与各种社会网络、神经网络及生物网络等有较高的拟合性)产生小世界网络,网络中的其他参数设置与1.1节中的随机网络相同。计算结果表明在没有噪声影响的情况下,SBL方法和L1算法在成功重构网络时所需的最小数据量是相近的(见图7和图8),L1算法和SBL算法成功重构囚徒博弈网络所需的最小数据量分别为0.35和0.38;重构雪堆博弈网络所需最小数据量分别为0.32和0.35。且SBL算法的收敛速度要优于L1优化算法(见图9)。图10~图12给出了2种算法在SNR分别为15 dB、10 dB和5 dB的情况下,PGD网络的重构结果。实验表明在噪声情况下,SBL算法有更好的重构性能。 (a) L1重构 (a) L1重构 图9 小世界网络中算法收敛时间比较 (a) L1重构 (a) L1重构 (a) L1重构 演化博弈网络是自然和社会系统中常见的一种互动类型,它在生物学、社会科学、经济学等领域有着重要的应用,探知演化博弈网络的拓扑结构是理解其功能和集体行为的基础。基于稀疏贝叶斯学习算法,本文进一步发展了有限数据下演化博弈网络的重构方法。与先前的基于L1范数重构方法相比较,稀疏贝叶斯学习方法同样能在较少的博弈信息下重构网路,且有更好的收敛性能,以及更强的噪声鲁棒性。本文的试验数据基于理论模型通过数值模拟产生,将该方法应用于实际数据分析和真实系统重构是面临的重大挑战。1.2 博弈网络重构
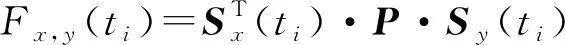
1.3 重构算法

2 数值模拟
2.1 随机网络



2.2 小世界网络






3 结束语
