基于LSTM神经网络的区域微网短期负荷预测

尹春杰,肖发达,李鹏飞,赵 钦

(山东建筑大学信息与电气工程学院,山东 济南 250101)

0 引 言

微电网是由分布式发电、储能系统和负荷组成的可控供能系统[1],作为大电网的一个发展分支，受到相关政策的鼓励，具有广泛、可观的发展前景。短期负荷预测在整个微电网能量调度管理系统中不可或缺，是对储能系统、柴油发电机及风力发电机等可控微源进行优化调度的基础[2-3]。此外短期负荷预测的结果也会影响整个微电网的安全稳定运行[4]和优化策略[5]的实施。

其主要体现在负荷预测的精度不高会增加微电网运行费用成本[6]，而且不能准确获得负荷的变化趋势，导致发电量产生波动，对其相连的大电网也会造成破坏。因此，提高微网电力负荷预测的精度无疑是当下亟待解决的一个问题。

微电网与传统大规模电网相比差异较大，微网短期负荷预测更加复杂[7-8]，主要由于微网用户容量小，负荷的随机性较强，负荷聚合的平滑效应弱，负荷的整体波动性较显著，变化比较剧烈[9]。对于微网短期负荷预测，文献[10]对微电网中分布式电源发电量和负荷量进行超短期预测，提出了剩余负荷的概念，建立起微电网剩余负荷预测模型。但是预测模型在一定时间段内预测相对准确，超出一定时间会影响预测的精度。文献[11]针对城市微电网系统中负荷的连续性和周期性，分析微电网负荷的特点，根据类似日的计算公式方法确立目标函数，基于SVM算法构造城市微电网预测模型，此模型改善了日负荷预测效果，但在个别时刻预测误差相对较大。文献[12]采用BP(Back Propagation)神经网络进行微网的短期负荷预测，合理规划了微网运行，但其也存在一定的局限性，仅能够有效利用微电网高负荷时间预测数据来缓解主网压力，提升其供电的可靠度。

本文采用基于循环神经网络(Recurrent Neural Networks, RNN)改进的长短期记忆(Long Short Term Memory， LSTM)神经网络构建微电网短期负荷预测模型。由于电力负荷数据是时间序列数据，使用LSTM相比传统神经网络以及RNN的优点是LSTM可以更好地学习负荷序列的长短期关联信息，不会因为时间过于久远导致相关信息的缺失[13]，适合解决此类问题。利用南京某地区工业负荷数据构建微电网预测模型并进行实验仿真，验证了基于LSTM神经网络微电网负荷预测模型的优越性。

1 LSTM循环神经网络模型

1.1 LSTM神经网络结构

针对RNN无法学习前后信息过于长久的弊端[14]，Hochreiter和Schmidhuber于1997年发表相关论文，提出LSTM神经网络模型[15]。改良后的LSTM网络解决了RNN模型因为时间久远梯度更新时梯度消失或膨胀的问题[16]，可以学习时间序列长短期关联信息[17]，在许多场景中得到了较好的应用。

如图1所示，给出了LSTM 网络的基本单元结构。其中包含了Forget Gate(遗忘门)、Input Gate(输入门)和Output Gate(输出门)。Forget Gate中输入xt、隐含层输出ht-1与状态记忆单元Ct-1共同决定了网络单元的遗忘区域。在Input Gate中，记忆单元中的2个保留向量由xt分别经过sigmoid变换和tanh变换后共同计算决定。一个隐层的输出ht由Ct变换更新后与变换后的ot共同计算决定,上述的计算如式(1)～式(7)：

ft=σ(Wfxxt+Wfhht-1+bf)

(1)

it=σ(Wixxt+Wihht-1+bi)

(2)

mt=ψ(Wmxxt+Wmhht-1+bm)

(3)

ot=σ(Woxxt+Wohht-1+bo)

(4)

Ct=mtit+Ct-1ft

(5)

(6)

(7)

其中，ft、it、ot、mt、ht和Ct分别为Forget Gate、Input Gate、Output Gate、输入节点、中间输出状态单元的态;Wfx、Wfh、Wix、Wih、Wox、Woh、Wmx和Wmh分别为相应门与输入xt和中间输出ht-1相乘的权重矩阵;bf、bi、bo、bm分别为相应门的偏置项;σ表示sigmoid变换函数;ψ表示tanh变换函数。

1.2 Adam优化算法

Adam优化算法是相对梯度下降法的一种拓展的优化算法，它可以根据损失函数计算网络中的梯度的一阶矩估计和二阶矩估计[18]，给网络中不同参数提供互不影响的自适应性学习率，而传统的梯度下降法却只能保持其单一不变的学习率。相关经验表明，Adam算法要优于AdaGrad、梯度下降法等算法。其流程如图2所示。

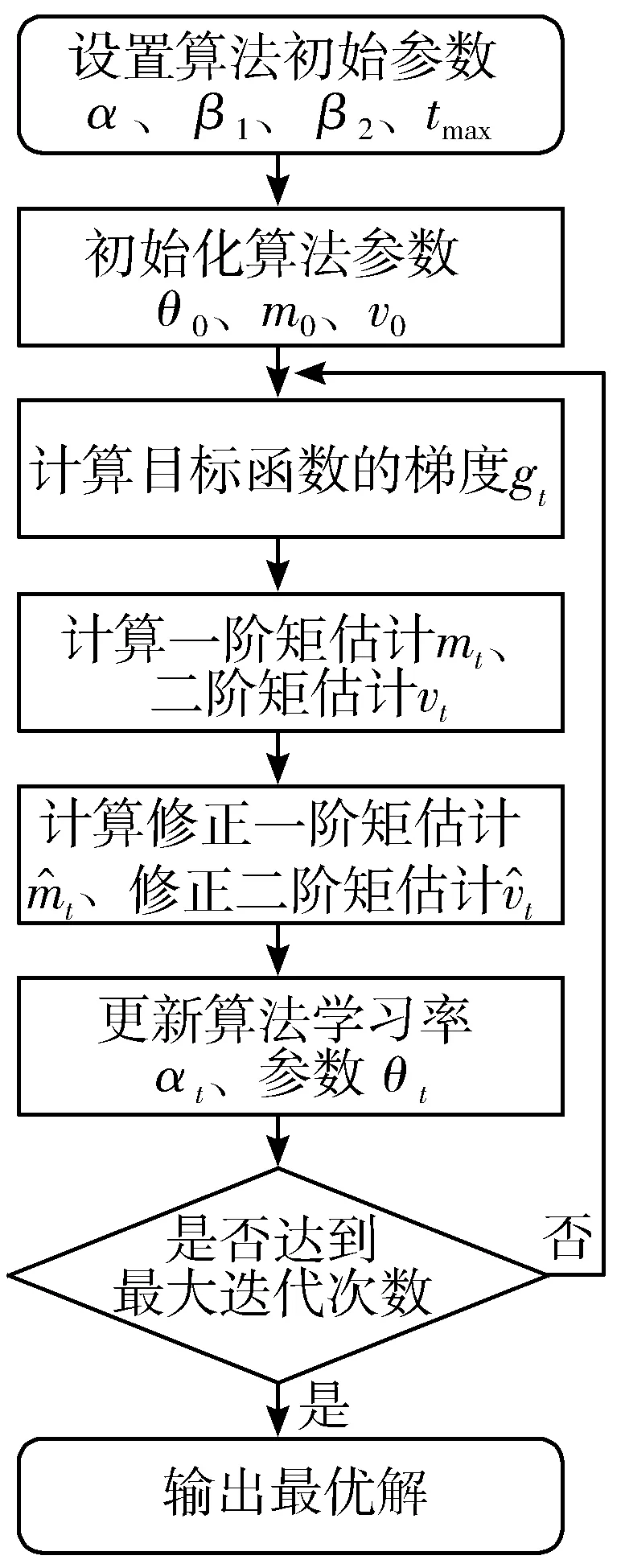
图2 Adam算法流程

上述算法流程图具体过程如下：

1)设置算法初始学习率α、一阶矩估计的指数衰减率β1、二阶矩估计的指数衰减率β2和最大迭代次数tmax。初始化网络权重参数θ0、一阶矩估计m0和二阶矩估计v0。

2)计算目标函数的梯度gt：

gt=▽θft(θt-1)

(8)

3)更新计算一阶矩估计mt和二阶矩估计vt：

mt=β1mt-1+(1-β1)gt

(9)

vt=β2vt-1+(1-β2)gt2

(10)

(11)

(12)

5)更新学习率αt和参数θt，重复上述步骤多次最终达到最大迭代次数tmax。

(13)

(14)

2 微电网负荷预测建模

2.1 影响因素分析

在微电网电力负荷预测中，预测的结果受多种因素的影响，但是易于获取的输入因素相对较少。例如气象因素、日类型等因素相对容易获取，而仅以此作为输入变量难以达到很好的效果，因此还需要选择其他因素作为输入变量。因为电力负荷具有一定的日周期特性和周周期特性[19-20]，同时具有“近大远小”[21]的特殊性，近期历史时刻的负荷值与当前时刻的负荷值具有非常紧密的相关性，所以选用这种周期特性的负荷以及相邻时刻的负荷作为输入影响因素比较具有参考价值。同时气象因素对于短期负荷预测有着至关重要的影响[22]。一般来说，众多影响的因素中最为常用且容易获取的气象因素就是温度。当前我们国家用电负荷以工业用电为主[23]，工作日的用电负荷量相比非工作日的用电负荷量明显增加，日类型也是一个不可或缺的影响因素。本文对输入变量的选择如表1所示。

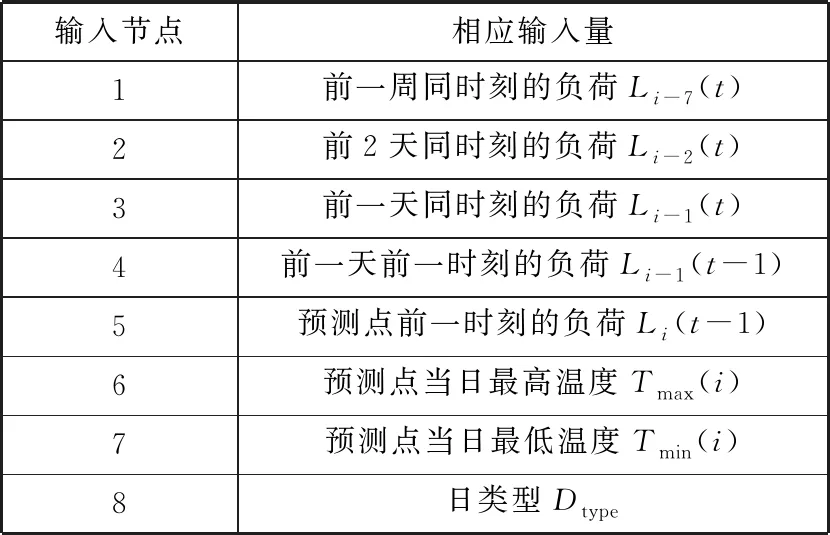
表1 负荷预测输入输出量

2.2 微网负荷预测模型

本文采取的短期负荷预测模型综合考虑历史负荷数据，最高、最低温度以及日类型(含工作日与休息日)。构建微电网短期负荷预测的模型如图3所示。

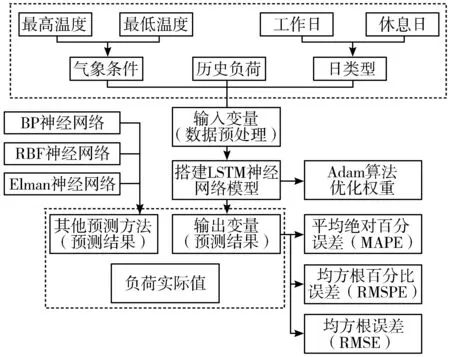
图3 微电网短期负荷预测模型

3 实验仿真

3.1 数据描述及平台

采用南京某地区区域微电网用户历史负荷数据对所提预测算法进行测试,数据来源于网络。提取2组负荷数据进行仿真验证，第1组数据时间长度为2002年11月—2003年1月，第2组数据为2003年6月—2003年8月。每间隔15 min进行一次数据采样。划分数据集,前60天的数据做训练,最后3天的数据做测试,预测未来3天负荷值。实验仿真分析所使用的计算机配置为i5-8265U处理器，8 GB的内存，仿真平台为Matlab2019a版本。LSTM实验仿真中Adam算法参数设置为tmax=250、α=0.005，经过125轮训练后通过乘以影响因子0.2来降低学习率，为防止梯度膨胀，设定梯度阈值为1。

3.2 输入数据预处理

此外，训练时如果存在较多异常的负荷数据将直接影响到短期内负荷预测分析结果的精确度以及可靠性，所以在开始进行网络训练前，对异常的数据进行预处理以保证其所有输入信息的质量。对异常的数据处理包括直接剔除异常值[24]和其他例如均值、众数、中位数来填补样本数据[25]的方法。然后，将预处理过的数据灌入模型，对实际应用模型进行训练。最后，训练出最佳的模型参数后，使用训练好的模型进行微电网的短期负荷预测。

为避免输入的数据取值范围差别较大、数据的分布不一致[26]而导致神经网络的收敛速度较慢、网络模型预测效果不佳的问题，对负荷量和温度等变量统一进行归一化处理。特别地，将日类型处理为：周一至周五用1表示，周六周日用0表示。常规归一化处理的公式为：

(15)

3.3 性能评价指标

平均绝对百分误差( Mean Absolute Percentage Error, MAPE) 是统计领域衡量预测准确性的一个重要指标[27]，在电力负荷预测领域的衡量中得到了广泛的应用。均方根百分比误差(Root Mean Square Percentage Error, RMSPE)和均方根误差(Root Mean Square Error, RMSE)也是作为评价模型好坏常用的指标，式(16)～ 式(18)分别给出了MAPE、RMSPE和RMSE的计算表达式。

(16)

(17)

(18)

3.4 结果分析

为了验证本方法的预测效果，采用LSTM神经网络与BP神经网络、ELMAN神经网络、径向基函数(Radial Basis Function, RBF)神经网络在同一组负荷数据下进行建模，通过4种模型来对比预测效果。

3.4.1 LSTM神经网络负荷预测分析

利用第1组数据进行分析，采用的训练集有5760条数据，测试集有288条数据，在LSTM神经网络节点数不同时的测试集所得到的结果如表2所示。

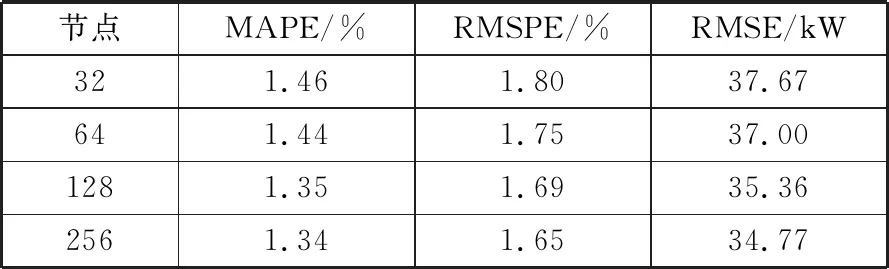
表2 LSTM测试集采用不同节点的测试结果

经实验分析对比，当网络隐含层节点数为128时误差相对较小，当节点数为256时，网络训练速度变慢但精度并没有得到很大的提升，所以本文预测模型选用128个节点作为隐含层节点数。

3.4.2 预测结果

通过2组数据验证来增强结果的可靠性，模型训练结束后，分别预测1月7日至9日及8月7日至9日的负荷数据。将LSTM神经网络与BP神经网络、Elman神经网络与RBF神经网络的预测结果进行对比，如图4和图5所示，所得的误差结果如表3和表4所示。

图4 1月7日至9日的预测结果

表3 1月实验误差对比

图5 8月7日至9日的预测结果

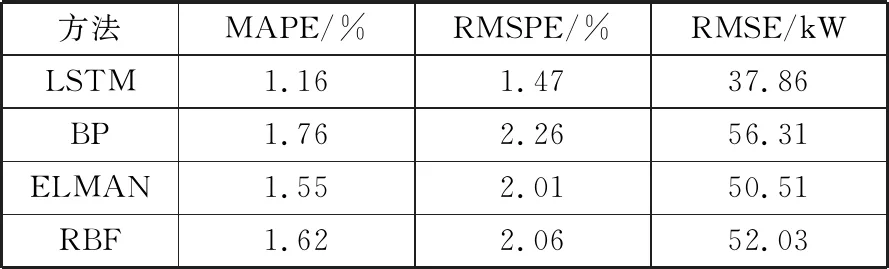
表4 8月实验误差对比

根据表4和表5可知，LSTM神经网络相比BP神经网络、Elman神经网络、RBF神经网络的误差有了明显的降低，这说明微电网中采用LSTM模型的预测结果相对来说较优。采用相同层数、节点，从预测结果的误差可以看出，采用同样的输入，微电网预测模型使用LSTM神经网络的预测精度更高，更加有效实用。

4 结束语

本文综合考虑了历史负荷、最高、最低温度和日类型作为输入变量，基于LSTM神经网络的方法，构建微电网负荷预测模型进行短期电力负荷预测，取得了比较理想的效果。

像电力负荷这类时间序列数据，利用传统的神经网络处理不能够记忆前后的关联信息而导致丢失掉一部分有用信息，从而导致预测结果不准确。RNN神经网络虽能够记忆信息，但是无法长久记忆历史信息，而LSTM神经网络凭借着其独特的网络单元结构，具有能够记忆长久信息的优点。采用Adam算法优化权重参数，保障了预测的稳定性，防止出现梯度爆炸和梯度消失的现象。

最后，将LSTM的预测结果与BP、Elman、RBF的预测结果进行对比，结果表明LSTM神经网络预测的精度更高，验证了微电网模型使用LSTM神经网络进行短期预测的有效性，具有很好的推广前景。