八波束相控阵换能器的研制
2022-05-05周博文许伟杰
周博文, 童 晖, 张 彬, 许伟杰
(中国科学院 声学研究所东海研究站,上海 201815)
无论是水面舰船还是水下潜器,在航行或水下工作时都需要高精度的定位和导航系统来获得位置和速度信息,DVL就是这样一种非常重要的导航设备[1-8],它可与其他导航设备组合使用,同时与其他导航设备相比,DVL还具有独特的优势。它可以测出载体相对于海底的绝对速度。对于利用波束形成技术的相控阵DVL,船速的计算与介质声速无关,从机理上消除了介质声速对测速精度的影响;除此之外,因只需一个平面基阵进行相控的收发,大大减小了基阵的尺寸,可实现设备的小型化[9-10]。
传统的DVL相控阵采用的是Janus配置方式[11],即向海底沿载体的前后左右方向发射4个波束。其中,DVL基阵阵元布阵间距通常为二分之一波长,即0.5λ,前后或左右方向上,两波束间与法线夹角分别为±30°。通过计算±30°方向上回波信号的多普勒频移,来计算载体的速度。此方法有着较高的精度,但由于只在载体前后或左右两个方向上各有两个波束,所收集的数据量有限,也限制了测速精度,除此之外,在某些非典型海底和不均匀水层的条件下,Janus配置方式的测量精度也会受到限制,因此,本文提出了一种八波束相控阵DVL,在载体前后和左右两个方向上分别有4个波束,是一种双Janus配置方式,其中,与水平面方向夹角较小的波束,可以提供更大的水平分量,有更大的作用距离,也更有利于进行多普勒频移的计算;与水平面方向夹角较大的波束,有着更大的垂直分量,使接收的回波信号有较大的信号强度,和更大的测速范围,两种波束优势互补。文章中提出的这种八波束DVL相控阵是在常规DVL相控方法的基础上进行了改进,采用了一种不同的相位施加方法。
1 理论推导
1.1 常规DVL相控方法
本文只针对DVL相控阵方法进行讨论。DVL是由多个线列阵组成的面阵。此处只对其中一线列阵进行讨论[12]。
如图1所示,假设有一个线列阵由N个(N为4的倍数)阵元组成,各个阵元的极性按图1中1~N个阵子所示的方式排列,相邻的两个阵元的间距均为d,且
(1)
利用这个线列阵来发射±θE方向、角频率为ω(波长为λ)的单频平面波。再根据乘积定理[13]:若由N=N1N2个阵元组成的复合阵,其中有N2个结构相同的子阵,且每个子阵有N1个相同的阵元构成,则此复合阵的指向性函数等于子阵中相同的阵元的指向性D1和各等效声中心组成的子阵的指向性D2的乘积。在此DVL相控阵中,每相邻的两个级性相反的阵元可看做一个子阵,假设第1个阵子输出电压为
u1(t,θ)=ejωt
(2)
与其相邻的第2个阵子的输出电压为
u2(t,θ)=-ejωt·ejφA
(3)
两个相邻阵元叠加电压为
u1,2(t,θ)=u1(t,θ)+u2(t,θ)
(4)
将式(2)和式(3)代入,得
u1,2(t,θ)=ejωt(1-ejφA)
(5)
进一步整理
(6)
由式(6)可以看出:由两个极性相反的点阵元组成的指向性阵元的声学中心在两阵元的中心处,该指向性阵元的指向性函数D1为
(7)
其中,
(8)
因此,
(9)
式中,d见式(1),因在θE方向相控形成波束,因此,在θE方向进行归一化,由于
(10)
因此,在θE方向上进行归一化后的指向性函数为
(11)
这里,D1(θ)在θE方向上等于1,但D1(θE)并不一定是D1(θ)的最大值。
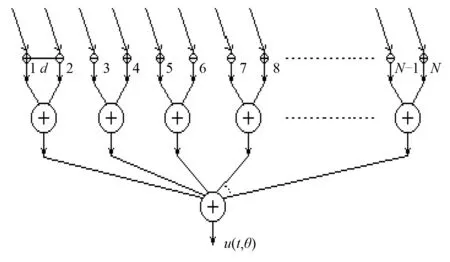
图1 线列阵示意图Fig.1 Schematic diagram of linear array
各等效声中心组成的子阵,长度为N2=N/2,阵元间距为2d,从而
(12)
又因相邻两个等效阵子电相位相差π,因此其指向性D2为
(13)
由于N是4的倍数,所以
(14)
将φA代入式(14),得
(15)
根据乘积定理,D(θ)=D1(θ)·D2(θ),可得最终指向性函数
(16)
在DVL相控阵中,通常±θE=±30°,即d=λ/2,根据式(16)计算可得,若N=32,则其指向性如图2所示。
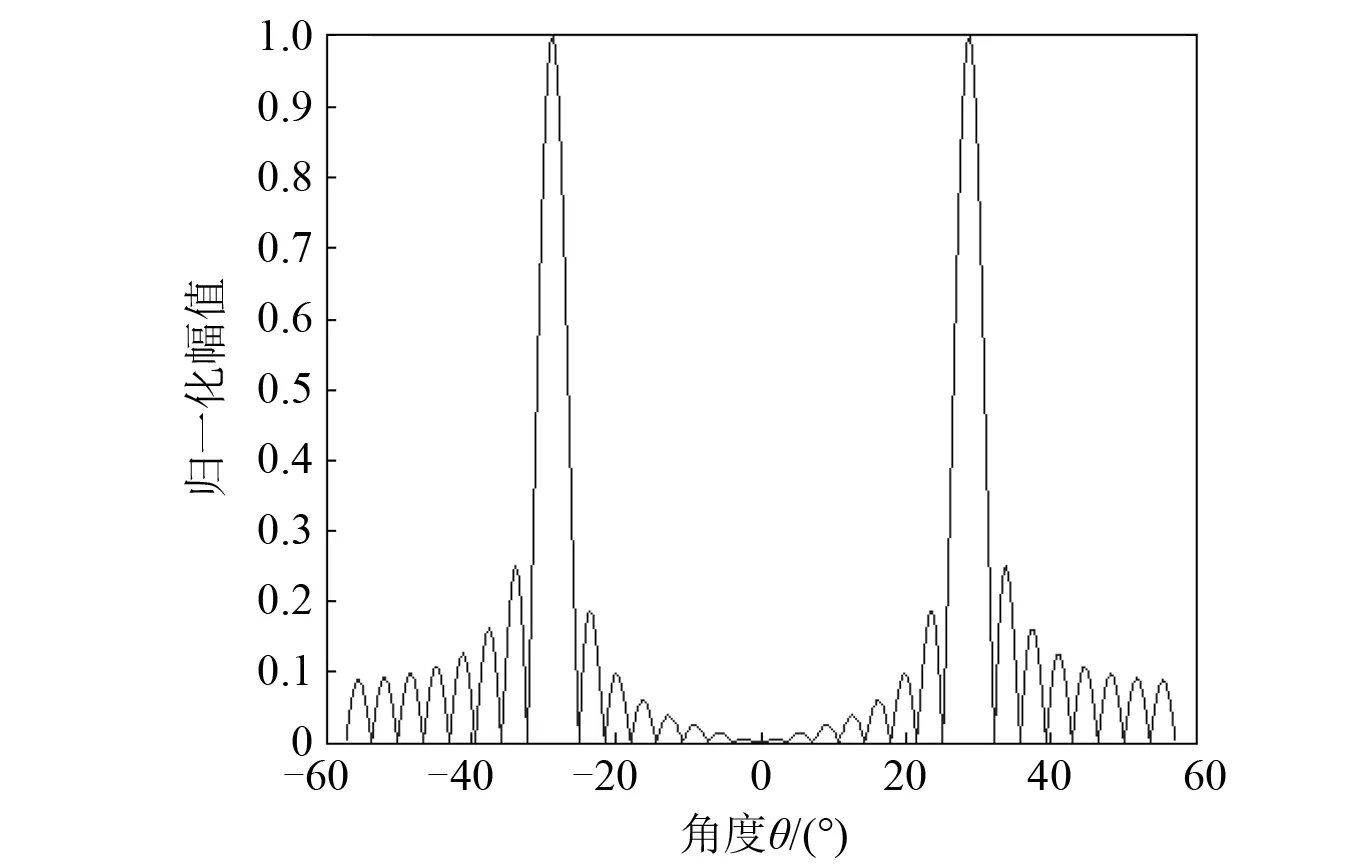
图2 线列阵指向性Fig.2 Linear array directivity
1.2 八波束相控阵方法
传统的DVL相控阵采用的是一种单Janus配置方法,其声束在声场远场,沿平行于基阵辐射面方向的截面示意图如图3所示,而八波束相控阵是一种双Janus配置方法,其示意图如图4所示。对比图3和图4可知,与传统的DVL相控阵相比,在水平方向和垂直方向上分别增加了两个波束。

图3 单Janus配置示意图Fig.3 Schematic diagram of single Janus configuration
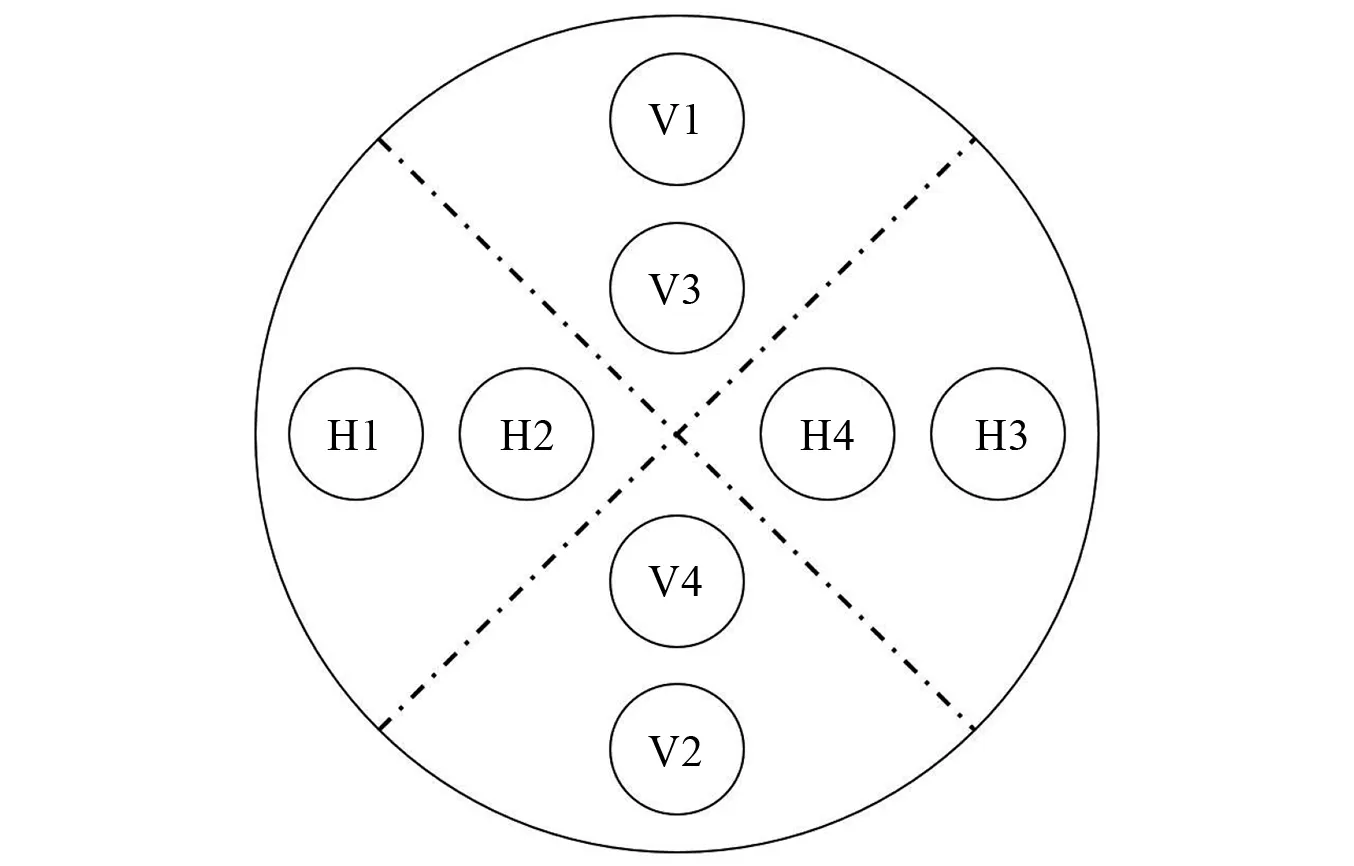
图4 双Janus配置示意图Fig.4 Schematic diagram of dual Janus configuration
基于上文对常规DVL相控阵指向性的推导,若其他条件不变,只改变阵元间距d与波长λ的比值,则主极大声轴方向偏离法线方向的角度亦将随之变化,如图5所示,图5中给出了d=0.35λ,d=0.5λ,d=0.7λ,d=λ四种情况的DVL相控阵的指向性图。其中:当d=λ时,出现了4个主极大值,所在角度分别为±48.52°和±14.54°,此时,靠近法线方向的两个主极大波束的夹角过小,实际工况条件下会导致回波信号分辨率不足;当d=0.5λ时,主极大波束所在角度为±30°,为常规DVL相控阵所用的角度;当d=0.35λ和d=0.7λ时,主极大波束所在角度分别为±45.77°和±20.99°。若选用d=0.5λ和d=0.35λ或者d=0.5λ和d=0.7λ的波束组合,则会出现波束相距角度太小的问题,同样会影响回波信号的分辨率,且实际布阵时,也很难同时满足两种阵元间距。因此,选用d=0.35λ和d=0.7λ的波束组合,既能在水平方向和垂直方向有较高的分辨率,同时,在布阵时又较为方便。

图5 不同间距线列阵指向性Fig.5 Linear array directivity with different spacing
结合上文所述,假设有一个面阵,采取稀疏阵布阵方式[14]进行布阵,其阵子中心距按d=0.35λ布阵,每一行阵元所加电压依次采用+--++--+…的方式。如图6所示的电路示意图,图中用“H+数字”和“V+数字”代表水平方向和垂直方向上的阵子,相同代号的阵子上施加同样的电压相位。以8个阵子为一个周期进行电压加载,例如:V1,V2,V3,V4,V5,V6,V7,V8,8个相邻的阵子分别对应施加+--++--+的电压,以此来进行相控,同理H路也是如此。按图中右下角箭头所指方向,沿水平虚线方向将形成水平方向的4个波束,沿垂直实线方向将形成垂直方向的4个波束。

图6 稀疏阵电路示意图Fig.6 Circuit diagram of sparse array
与此同时,在同一行中,若将相邻两个阵子看做一个阵子,也按照+--++--+…的方式施加电压,即相当于是阵子中心距按d=0.7λ布阵,如图7所示。图7中:第1行为两个周期,16个阵子的排布;第2行为每个阵子对应所施加的电压;第3行为将相邻两个阵子看做一个阵子后的等效阵子;第4行为等效阵子所施加的电压;第5行为将在每个阵子上所施加的两种电压相加后所获得的新电压。这样,对于此线列阵来说,两种电相位叠加后,同一行中,一个周期内的8个阵子所施加的电压依次为+0-00-0+…,如此,即可在一个方向上形成4个波束。
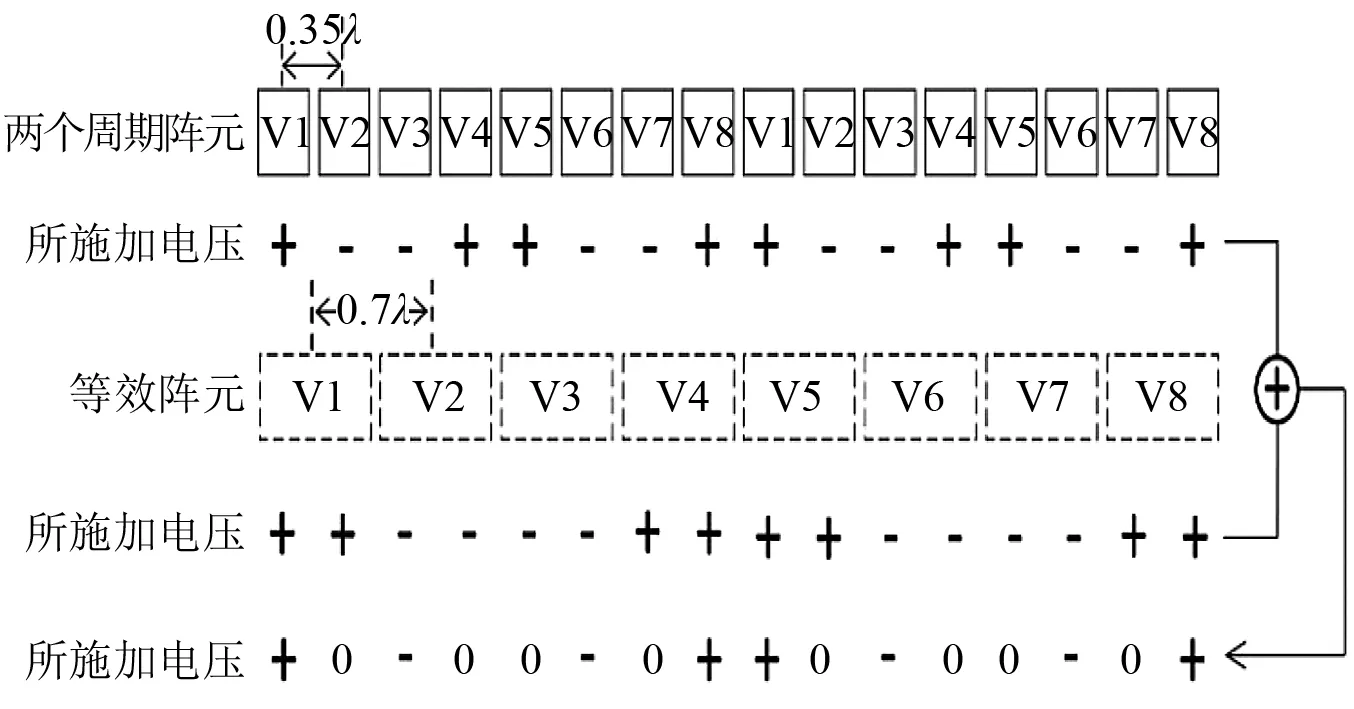
图7 八波束相控阵V路相位叠加原理图Fig.7 Phase superposition schematic diagram of eight beam phased array V channel
利用上述相控方法,通过仿真计算可得,当阵子中心距按d=0.35λ布阵时,同一方向上,4个波束主极大所在位置分别为±43.56°和±20.16°,如图8所示。图8中:第1行为阵元间距为d=0.35λ时的指向性图;第2行为阵元间距d=0.7λ时的指向性图;第3行为两种电相位叠加后的指向性图。

图8 八波束相控阵指向性仿真Fig.8 Directivity simulation of eight beam phased array
2 试验结果
根据上述仿真结果,在实验室制作了一个直径Φ=90 mm、中心频率300 k的换能器基阵。换能器采用1-3型复合材料[15],其中的每一个颗粒为一个阵元,阵元布阵间距d=0.35λ,换能器灌封后实物图如图9所示。4990A阻抗分析仪测得各单路阻抗曲线和相控后的阻抗曲线如图10~图12所示。其中:图10为V路其中四路的阻抗曲线;图11为H路其中四路的阻抗曲线,由图11中可知,V路和H路阻抗曲线一致性较好;图12为V路各路相控后的阻抗曲线,300 k工作频点处的电导值为2.83 mS。

图9 换能器实物图Fig.9 Transducer physical map
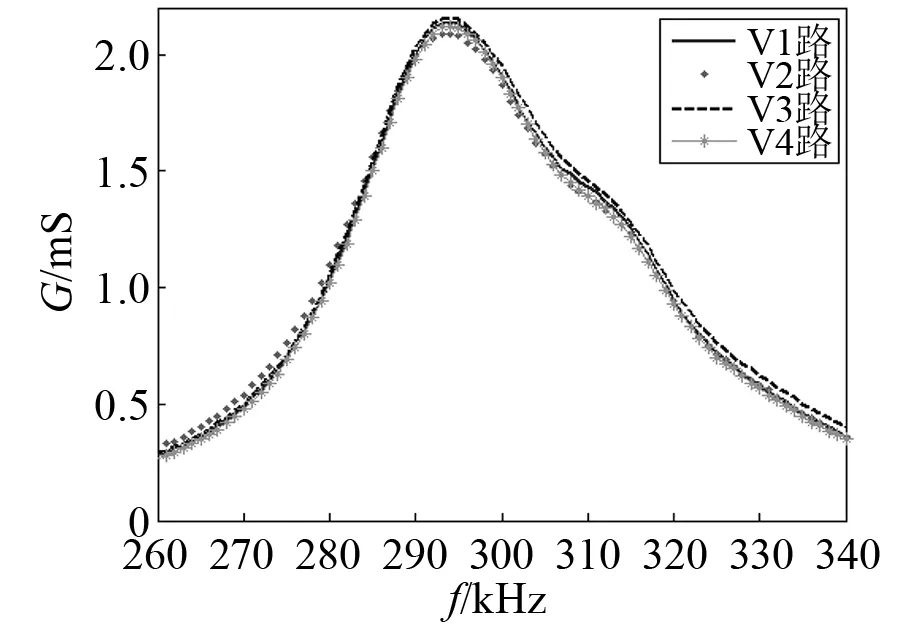
图10 换能器V1路-V4路的水中阻抗曲线Fig.10 Underwater impedance curve of transducer V1-V4
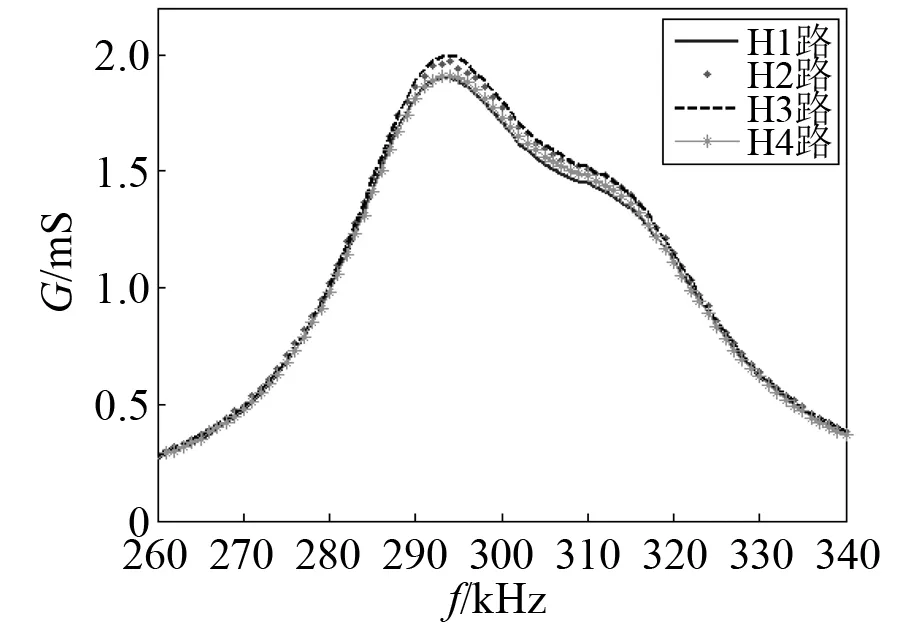
图11 换能器H1路-H4路的水中阻抗曲线Fig.11 Underwater impedance curve of transducer H1-H4
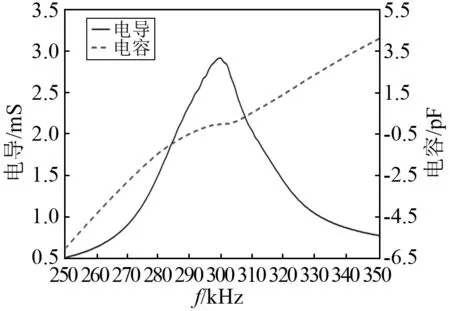
图12 八波束相控阵水中阻抗曲线Fig.12 Eight beam phased array underwater admittance curve
以水平方向为例,在消声水池测得其指向性如图13~图15所示。其中:图13为阵元间距d=0.35λ时的指向性图;图14为阵元间距d=0.7λ时的指向性图;图15为两种相位叠加后的指向性图。图中:菱形细线为理论值;粗实线为实测值;理论值和实测值的内外侧波束角度、内外侧波束最高旁瓣级以及内外侧波束开角的具体数值如表1所示,由表1对比发现,理论值和实测值吻合较好。文中提出的这种相控阵换能器对各阵子的一致性要求较高,因此,在实际的换能器制作中,若不能保证各阵子以及各阵子间距的较高的一致性,则在相控后,会在其他不关心的方向上也出现波束,从而影响相控的效果。
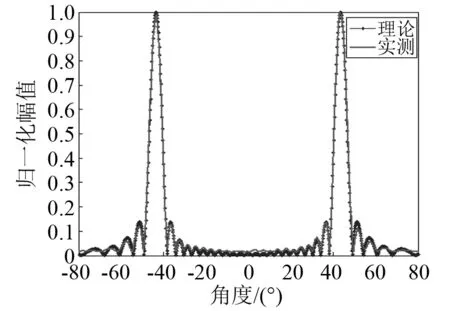
图13 当d=0.35 λ时指向性Fig.13 Directivity of d=0.35 λ
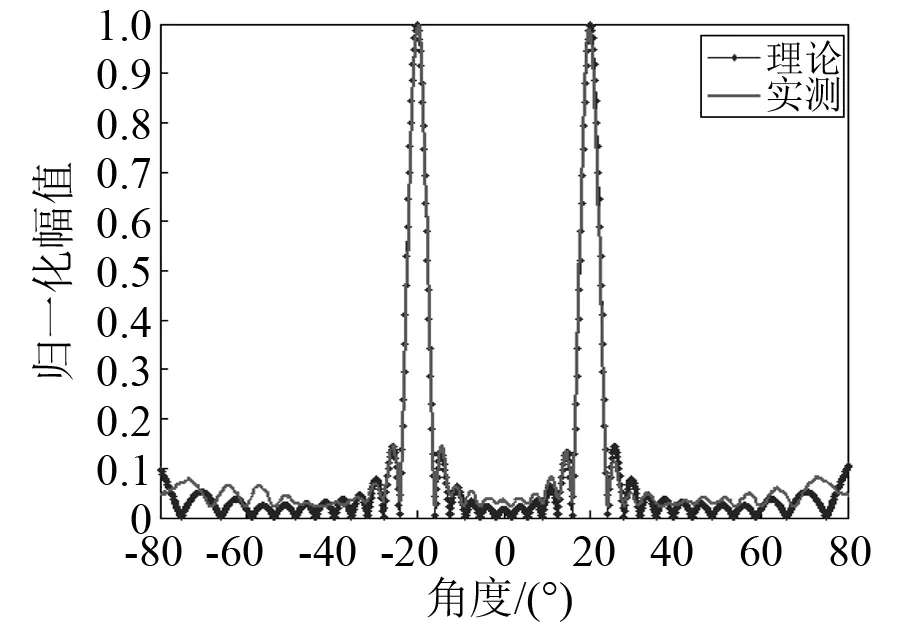
图14 d=0.7 λ时指向性Fig.14 Directivity of d=0.7 λ

图15 两种相位叠加后的指向性Fig.15 Directivity after superposition of two phases

表1 理论与实测值对比
发送电压响应理论计算公式为
(17)
式中:Z为换能器工作点阻抗值;η为发射效率;DI为聚集系数,其表达式为
(8)
根据式(18)计算可得,在300 kHz处的发送电压响应理论计算值为170.3 dB,在消声水池测得外侧波束和内侧波束的发射电压响应,分别为170.2 dB和170.6 dB。
传统的DVL只需对阵子依次施加+--++--+的电压,即可实现4个波束的相控,而本文提出的八波束DVL是对阵子依次施加+0-00-0+的电压,两种施加电压的方式进行对比可发现,从阻抗值的角度看,传统的DVL要比八波束DVL的电导值高一倍。结合式(17),可计算出同样尺寸的换能器,传统的DVL要比八波束DVL的发射电压响应高3 dB。因此,本文中所制作的换能器若按传统DVL方式实现相控,则发送电压响应值应为173.3 dB。
3 结 论
本文提出了一种八波束的相控阵换能器,是在传统的Janus配置基础上,通过对不同的阵子同时施加两种不同的电相位,从而实现双Janus配置的八波束的换能器。本文中所制作的换能器同一方向4个波束所在角度分别为±43.49°和±20.10°,发送电压响应分别为170.2 dB和170.6 dB。这种八波束相控阵换能器相对于传统的单Janus配置的多普勒计程仪,在水平和垂直方向分别多出两个波束,大角度的波束,可以提供更大的水平分量,有更大的作用距离;小角度的波束,有着更大的垂直分量,使得接收的回波信号有较大的信号强度。若结合整个DVL测量系统,将会有更高的测量精度,在某些非典型海底和不均匀水层的条件下,会具有更好的适应性。
