求解可分离凸优化问题的惯性近似松弛交替方向乘子法

薛中会， 殷倩雯， 党亚峥

（1. 上海出版印刷高等专科学校，上海 200093；2. 上海理工大学 管理学院，上海 200093）

1 问题的提出

一个优化问题如果满足：称该问题为一个凸优化问题。其中，目标函数f为凸函数，不等式约束gi也为凸函数，而等式约束hj为一个仿射函数。

一个可分离的凸优化问题为

交替方向乘子法（ADMM）是一种求解具有可分离的凸优化问题的重要方法。由于其处理速度快、收敛性能好，ADMM 算法在统计学习、机器学习等领域有着广泛应用，在求解可分离凸优化问题上具有简单、灵活、实用性强的效果。其优势在于利用对偶上升算法的可分离性，可以将大规模问题拆分成2 个甚至多个小规模的子问题，随后交替求解分解所得的各个小规模子问题，从而提高了求解问题的效率。ADMM 算法最早由Glowinski 等[1]和Gabay 等[2]提出，ADMM 算法的经典迭代步骤为

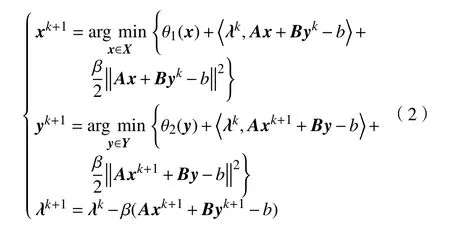
ADMM 在每一步迭代中都能解决较简单的子问题，并且可以分别利用f(x)和g(x)的结构。众所周知，如式（1）具有KKT 点，则由式（2）生成的对偶序列收敛到对偶问题的最优解，但是，在没有附加条件的情况下，原始迭代序列不一定收敛。为了改善原始收敛性，Eckstein[3]首先通过向式（2）的子问题添加一些二次项，提出了邻近ADMM算法。经研究发现，惯性技术也可以加入ADMM算法中，在适当的假设条件下能够加速算法的收敛效果。Alvarez[4]最早提出惯性技术这一概念，其基本思想是利用当前迭代和上一步迭代之间的相关联系得到下一步迭代，这样不仅能够较快地得到所求问题的最优解，而且在收敛性证明上也相对容易。近年来，惯性技术被运用于邻近点算法（PPM）求解极大单调算子包含问题。通常情况下，为了加速邻近点算法的收敛速度，考虑二阶微分包含问题

基于惯性技术在加快收敛性方面具有很好的效果，本文对可分离凸优化问题采用惯性技术，同时引入随机加速的随机变量以更新步长，提出了惯性近似松弛交替方向乘子法。在适当的假设条件下，基于惯性邻近点法的收敛性证明了惯性邻近ADMM 算法的收敛性。另外，数值实验验证了新算法在实践中具有更好的数值表现。

2 预备知识

则f在C上是单调的。

RnF:C→Rn

如果C是 上的一个紧凸集，且 是一个连续映射，那么，变分不等式问题(VIP)至少有1 个解。进而可知，若函数是单调的，那么，变分不等式问题的解存在且唯一。

3 惯性近似松弛ADMM

现针对可分离凸优化问题构建惯性近似松弛交替方向乘子法（IPR-ADMM）。

问题（1）的增广拉格朗日函数为

c. 停止准则。计算

4 收敛性证明

现利用变分不等式证明算法1 的全局收敛性。根据式（8）的变分不等式形式生成如下形式的迭代方案：

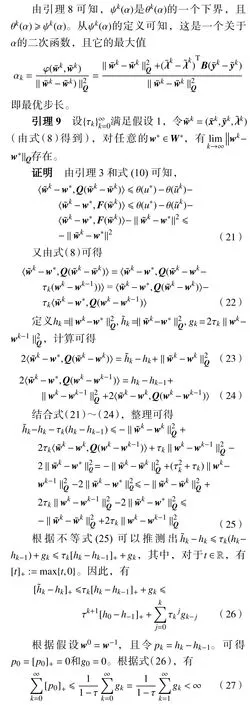
其中，第2 个不等式由假设1 的b 得到。

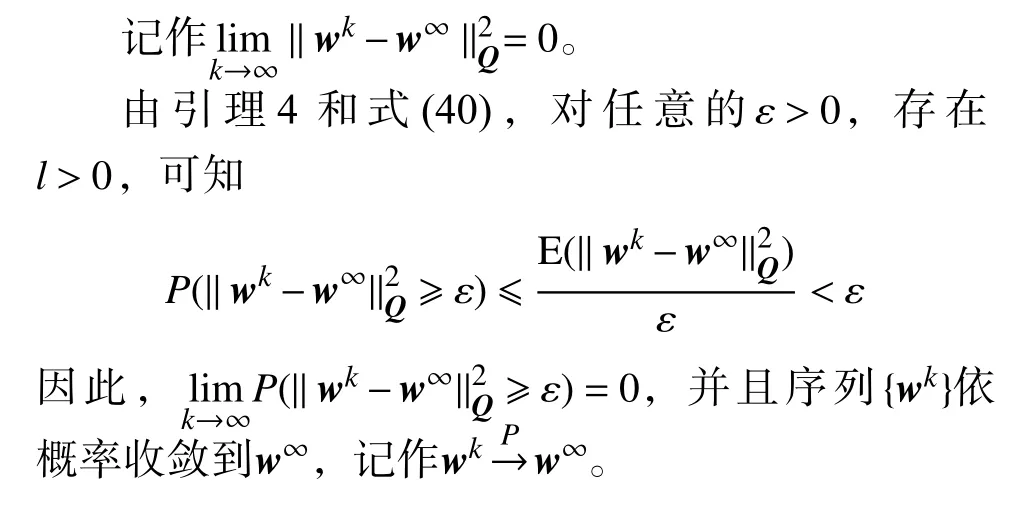
5 数值实验

数值实验所用软件为Matlab 2017b，电脑配置为Intel 四核i7 2.4GHz CPU，并在Vista 操作系统上运行8GB RAM。

例1 首先考虑财务和统计问题[15]，

迭代式（43）的X-子问题通过奇异值分解（SVD）进行求解，它承担每次迭代过程中的主要计算负荷。迭代式（43）的Y-子问题是一个投影，有如下形式：

表1 为参数R,S取不同值时的数值实验结果；表2 为参数 τk取不同值时的数值实验结果；表3 为期望值 ρ取不同值时的数值实验结果。其中，n表示不同的维数，取50，100，200。显然，从表1～3 可以看出，R，S的取值越大，迭代次数越少，算法收敛所消耗的时间也越少；而参数 τk的值越小，算法表现出的数值性能越好。此外，随机变量的不同期望值 ρ产生的迭代次数相近，在ρ=1.9时表现相对较好。综上，惯性技术和随机变量更新步长都有利于加速算法的收敛。

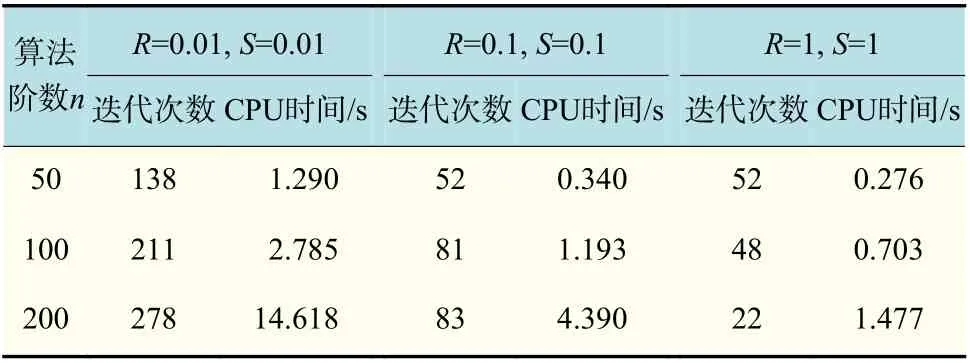
表1 参数R, S 不同取值的数值结果比较Tab.1 Comparison of numerical results on different values of parameters R and S

表2 参数 τk不同取值的数值结果比较Tab.2 Comparison of numerical results with different values of parametersτk

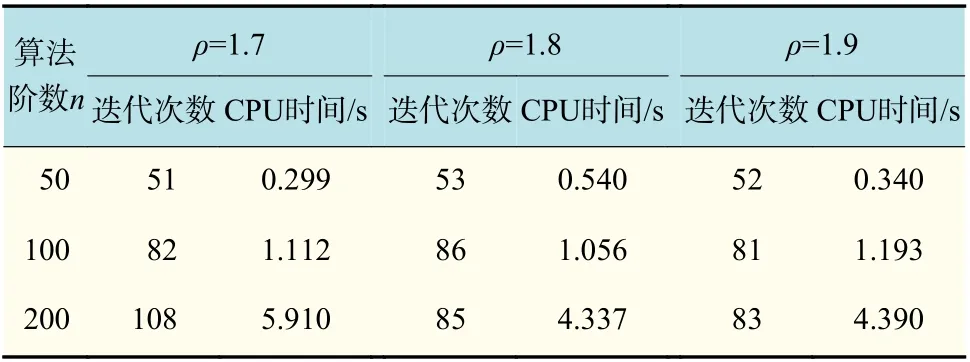
表3 期望值ρ 不同取值的数值结果比较Tab.3 Comparison of numerical results with different values of expected value ρ

表4 为不同维数下分别应用IPR-ADMM 和ePADM[49]解决该问题所用的时间和迭代次数。其中，n=50，100，200。s为迭代所用的时间，k为迭代次数。惯性近似松弛ADMM 算法中参数τk=0.5， 随机变量 ηk的期望值 ρ=1.9。

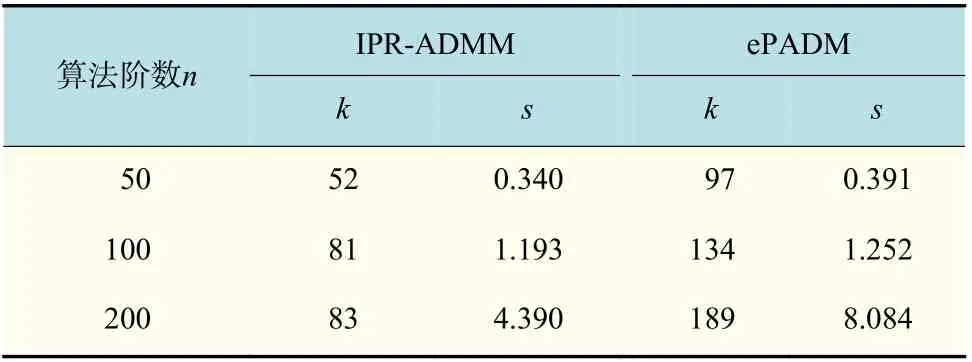
表4 例1 的数值结果(ρ=1.9)Tab.4 Numerical results of example 1 (ρ=1.9)

图1 为n=50，100，200 的条件下，IPR-ADMM和ePADM 算法的对比结果。其中，横轴表示迭代次数，纵轴表示停止准则，即收敛停止时间。显然，由表4 和图1 可以看出，算法1 的性能明显比ePADM 算法好，因为它的迭代次数和计算时间要少得多；并且从图1 看出，n的取值越大，算法收敛越快，越趋于稳定。

图1 ePADM 和IPR-ADMM 算法对比（ρ=1.9）Fig. 1 Comparison of ePADM and IPR-ADMM algorithms（ρ=1.9）

结果表明，算法1 对于解决问题（1）是有效的，而且算法1 的性能更良好，实验结果展现了加速策略的有效性。

6 结 论

通过应用PPM 算法求解ADMM 分解的子问题，并使用惯性外推项，构建了一种用于求解线性约束可分离凸问题的乘数的惯性近似交替方向方法，而且使用随机变量来加快收敛速度。在适当的假设下，证明了该方法的全局收敛性。数值结果表明，该算法是有效的，收敛效果优于现有算法。