基于mRMR-BP算法的辛烷值损失预测模型研究

姬子恒，朱建伟，陈海江

（长安大学 机械学院，西安 710064）

0 引 言

汽油是小型车辆的主要燃料，汽油燃烧产生的尾气排放对大气环境影响严重。汽油清洁化的重点是降低汽油中的硫、烯烃含量，同时保持其辛烷值。中国每年从国外进口大量的含硫和高硫的原油，且其中的重油通常占比高达40%-60%。为了有效利用重油资源，中国开发了一种以裂化催化为核心的重油轻质化工艺技术，将重油转化为汽油、柴油和低碳烯烃。为了满足对汽油质量的要求，必须对催化裂化汽油进行精制处理，降低其中的硫、烯烃含量。然而，现有的技术在对催化裂化汽油进行脱硫和降烯烃处理过程中，普遍降低了汽油辛烷值，影响了汽油的燃烧性能。据研究结果表明，辛烷值每降低一个单位，相当于每吨损失150元。因此，在汽油精制过程中尽量保持其辛烷值，是提高石化企业经济效益的关键。

为了控制汽油精制处理过程中辛烷值的含量，本文将通过数据挖掘技术，建立汽油辛烷值（RON）损失的预测模型，并给出每个样本的优化操作条件。

1 寻找建模主要变量

某石化企业的催化裂化汽油精制脱硫装置运行4年，积累了大量历史数据，其中包括7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质以及354个操作变量，合计367个变量。如此庞大的样本数据，不利于建模过程的优化。因此，需要通过降维的方法，从367个变量中筛选出建模主要变量，使得降维后的主要变量减少为30个以下，并使主要变量之间尽量具有代表性和独立性。建模主要变量筛选流程如图1所示。

图1 建模主要变量筛选流程Fig.1 Flow chart of main variables screening in modeling

1.1 互信息法

在对海量数据或大数据进行数据挖掘时，通常会面临“维度灾难”。其原因是数据集的维度可以不断增加直至无穷多，但计算机的处理能力和速度却是有限的。典型的数据降维思路，是基于特征选择的降维。本文采用基于统计分析的方法，通过计算汽油精制过程中不同操作变量与汽油辛烷值之间的互信息量，对求出的互信息按大小进行排序，筛选出其中排序靠前的若干个变量。

通常情况下，两个离散变量和的互信息如图2所示，可定义为：

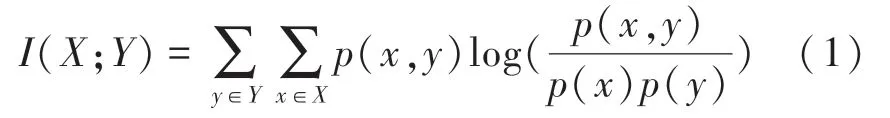
其中，（，）是和的联合概率分布函数，而（）和（）分别是和的边缘概率分布函数。

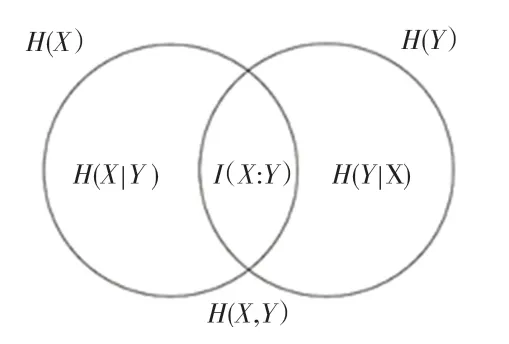
图2 互信息示意图Fig.2 Schematic diagram of mutual information

当求解某个变量与辛烷值的联合分布密度（，）时，可根据随机变量、的取值范围，将整个区域等分为100个小网格，对于任意一个小网格xy，定义联合分布密度（x，y）p，其值为落在该小网格上的样本数据点数与样本数据总点数之比。

当分别求解某个变量与辛烷值的边缘概率分布函数（x）和（y）时，可分别对联合分布列的第行和第列的联合概率密度求和，即：

将其代入公式（1），即可求出第个变量与辛烷值的互信息（；），共计366个互信息值。将这些变量的互信息值按从大到小的顺序排列，筛选出排序靠前的变量，即与辛烷值的相关性最高的若干变量。

1.2 mRMR算法特征选择

mRMR算法主要是为了解决通过最大化特征与目标变量的相关关系度，得到的最好的个特征中存在冗余特征的问题。采用mRMR算法可以筛选出辛烷值的操作变量中相关性较小的变量，保证了可操作变量与辛烷值之间最大相关性的同时，彼此之间又有最小的冗余性。

首先，利用互信息计算（；）（（；）越大，其之间的关联度就越大）。找出含有（x）个特征的特征子集，使得找出的个特征和类别的相关性最大，即找出与关系最密切的个特征。

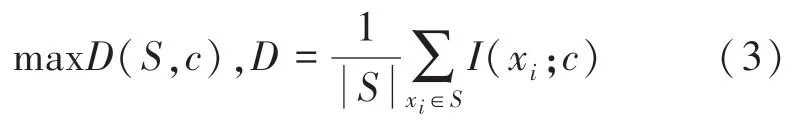
特征集与类别的相关性由各个特征x和类之间的所有互信息值的平均值定义，由此选出个平均互信息最大的集合。之后，消除个特征之间的冗余：

最终，筛选出同时满足与辛烷值之间具有最大相关性，且彼此之间又有最小冗余性的18个可操作变量。

2 建立辛烷值（RON）损失预测模型

通过比较每个自变量和因变量之间互信息的大小，把互信息值大的变量筛选出来，最终得到了18个用于建模的主要变量。本文主要利用BP神经网络，对辛烷值损失建立预测模型。

2.1 BP神经网络构建

BP神经网络属于前向神经网络，强调网络采用误差反向传播的学习算法。其中包括一个输入层、若干隐含层和一个输出层组成。其核心思想是通过样本训练集，不断修正神经网络的权值和阈值，逐步逼近期望的输出值。在训练开始时沿着网络正向传播，然后根据网络的输出值与期望的输出值之间的误差，反向传播调整权值和阈值。通过反复更新网络权值和阈值实现误差最小，即完成网络训练。本文设计的网络结构示意如图3所示，其实现步骤如下：

设计网络结构层

（1）输入输出层：将提取的18个主要变量作为输入，产品辛烷值损失量作为输出。故输入层神经元个数18，输出层神经元个数1。

（2）隐含层：在网络设计过程中，隐含层神经元数的确定十分重要。隐含层神经元个数过多，会加大网络计算量，并容易产生过度拟合问题；而神经元个数过少，则会影响网络性能，达不到预期效果。由于，涉及数据较少，本文设置迭代次数为1000，训练误差目标为0.000001，学习率为0.4。分别设定隐含层神经元数为：45，60，90，120，在此基础上讨论不同隐含层神经元数的测试误差。误差平均值见表1。

表1 不同隐含层神经元数的误差均值Tab.1 Error mean of neurons in different hidden layers

从表1可以看出，当隐含层神经元数为90时，误差均值最低。因此，设置隐含层神经元数为90。

图3 神经网络结构示意图Fig.3 Structure diagram of neural network

确定训练数据和测试数据

通过前文的指标筛选，得到325行18列的变量数据，即神经网络的输入层数据，输出层数据为325行1列的数据。本文设置前260行数据为训练数据，后65行为测试数据。基于此，数据标准化按照公式（6）进行。

选取激励函数

激励函数的作用是提供规模化的非线性化能力，使得神经网络可以任意逼近任何非线性函数，模拟神经元被激发的状态变化。若不用激励函数，无论神经网络有多少层，输出都是输入的线性组合。

目前，常用的激励函数有：Sigmoid、Thah和ReLU。ReLU使得SGD的收敛速度比Sigmoid和Thah快很多，使过程计算量减少，此外还解决了梯度消失问题。出于此种考虑，本文选择ReLU（Rectified Linear Uni）作为本神经网络的激励函数。其形式如下：

上述算法流程如图4所示。

2.2 预测模型验证

对降维后筛选出18个主要变量的325个样本数据进行BP神经网络分析，经过数据训练与学习，产生辛烷值损失的预测结果。将测试集导入训练好的RON损失预测模型中，对预测得到的结果与其真实值进行对比，其结果如图5所示。

图4 BP神经网络算法框图Fig.4 Block diagram of BP neural network algorithm

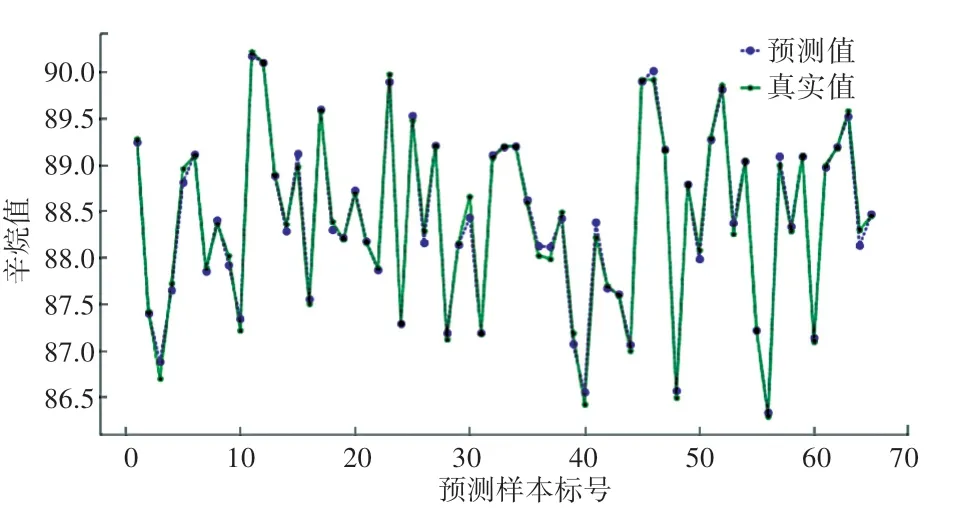
图5 BP神经网络预测结果与真实值对比Fig.5 Comparison between BP neural network prediction results and real values

从图5可以看出，预测值与真实值十分相近，说明该模型具有较好的回归结果，可较为真实的反应辛烷值的损失。各样本预测误差百分比计算结果如图6所示。

图6 BP神经网络预测误差百分比Fig.6 Percentage of prediction error of BP neural network

从图6可以看出，训练得到的BP神经网络模型预测结果较为准确，样本中预测的误差百分比最大只有0.25%。

3 主要操作变量对辛烷值损失的影响

经查阅相关文献可知，在S Zord吸附脱硫技术中，主要有烯烃加氢饱和反应和烯烃异构化反应。而烯烃加氢饱和会形成烷烃，从而大大降低精制汽油的辛烷值，使辛烷值损失过大。因此，为了减少精制汽油的辛烷值损失，应该抑制烯烃的加氢饱和反应，增强汽油在反应器中的烯烃异构化反应。

3.1 再生吸附剂S含量

在S Zord实际的生产过程中，主要通过再生吸附剂的含量来调整吸附剂的活性。由优化分析可知，当调整主要操作变量——再生吸附剂含量，该主要操作变量的含量越高，再生吸附剂的活性就越大，精制汽油的辛烷值损失就越小。因此，在保证精制汽油的硫含量不大于5μg／g的前提下，尽可能提高再生吸附剂含量，从而降低精制汽油中的辛烷值损失。

3.2 F-101循环氢出口管温度

由于烯烃加氢饱和反应是强放热的过程，所以通过增加反应温度，可有效抑制此反应的进行。如果反应器内烯烃加氢饱和反应大量发生，则反应器的温度将会大幅度提高，同时耗氢量也会增加。总而言之，烯烃加氢饱和反应是S Zord装置脱硫过程最不希望发生的反应，所以应尽可能通过调节反应温度、反应压力、再生吸附剂含量等主要操作变量来抑制此反应的发生。反应温度对辛烷值损失的影响曲线如图7所示。

图7 反应温度对辛烷值损失的影响Fig.7 Effect of reaction temperature on octane number loss

3.3 反吹气体聚集器／补充氢差压

由于烯烃加氢饱和反应是一个体积减少的过程，增加反应压力将促使氢分压增加，使烯烃加氢的速率增加，从而加速了烷烃的形成，导致精制汽油中的烯烃含量的减少，增加辛烷值的损失。所以，合理有效地控制反吹气体聚集器／补充氢差压，降低反应压力则会减少辛烷值的损失。反应压力对辛烷值损失的影响曲线如图8所示。

图8 反应压力对辛烷值损失的影响Fig.8 Effect of reaction pressure on octane number loss

4 结束语

本文构建了基于mRMR-BP算法的辛烷值损失预测模型，通过互信息和mRMR算法筛选出主要操作变量，解决了传统的数据关联模型中变量相对较少的问题，使主要操作变量更具有代表性和独立性。经对模型验证，表明该模型在预测精度上有较好的表现。通过分析主要操作变量对辛烷值损失的影响，为企业汽油精制处理过程中的实际操作提供可靠参考，帮助企业实现经济效益最大化。