圆筒型FPSO 在波浪中运动响应特性研究
2022-05-05王朝阳贾鲁生
李 刚 李 达 王朝阳 易 丛 贾鲁生
(中海油研究总院有限责任公司 北京 100028)
0 引 言
浮式生产储卸油装置(FPSO)作为海洋油气田开发的重要装备,尤其是对于离岸较远、周边缺少管网依托的油田,往往成为海上油田开发的一种经济有效模式。我国从上世纪80 年代开始在南海北部湾首次采用由旧油轮改造而成的FPSO,1989年首艘自主设计建造的FPSO“渤海友谊号”在渤海油田投入使用。经过三十多年的发展,我国FPSO 整体技术已达到世界领先水平,并已成为全球FPSO 制造与使用大国。我国在南海和渤海的油田开发中已投入使用了20 艘FPSO,FPSO 载重量包括5 万吨级、10 万吨级、15 万吨级以及30万吨级。我国所拥有的FPSO 数量和总吨位均位居世界前列,FPSO 对支撑我国海上油田产能建设、保障我国的能源供应作出了重要的贡献。
目前,我国海上油田开发所使用的FPSO 均为船型FPSO,船型FPSO 通常需要采用单点系泊系统使其长期系泊定位在油田附近海域。单点系泊系统可使FPSO 具有“风向标”效应,允许FPSO 在风浪流作用下绕单点系泊系统自由旋转,使FPSO始终承受最小的环境载荷。此外,单点系泊系统还发挥传输井流、电力和通讯等作用。单点系泊系统是船型FPSO 的核心组成部分,其技术长期被欧美国家的单点公司所垄断,整体投资高昂、供货周期较长,导致船型FPSO 的整体工程投资很高。同时,船型FPSO 对环境条件较为敏感,运动响应(尤其是垂荡运动性能)相对其他浮式装置差,应用于深水油气田开发会给回接至FPSO 上的立管设计和应用带来较大的挑战。
近年来,圆筒型FPSO 作为一种新型海洋工程装置,逐渐被应用于全球海洋油气资源的开发。2007 年,全球首座圆筒型FPSO“Sevan Piranema”在巴西投产使用。目前,全球已有5 座圆筒型FPSO 分别在巴西、英国北海和挪威北海投入使用,作业水深从100 m 到1 000 m 左右。与传统船型FPSO 类似,圆筒型FPSO 同样具有油气水生产处理、储油、外输及生活居住等多种功能,但其圆柱型船体为对称结构型式,采用多点系泊系统进行定位,很少采用造价较为高昂的单点系泊系统。圆筒型FPSO 在船体底部采用比船体直径更大的阻尼板,以增加附加质量和阻尼,改善其运动性能。
在圆筒型FPSO 运动性能预报方面,黄佳等通过水池模型试验对圆筒型FWPSO 的纵摇和垂荡运动性能进行了研究,并将圆筒型FPSO 运动响应的数值预报结果与模型试验结果进行对比分析;童波等采用CFD 方法对不同阻尼结构的圆筒型FPSO 垂荡运动性能进行了研究,验证新型阻尼结构的阻尼性能优于传统垂荡板;刘波基于三维势流理论对几种典型浮式结构物在南海环境条件下的运动性能进行了对比研究,证实了圆筒型FWPSO 在中国南海的适用性;AARSNES J V 等和VIDEC-PERUNOVIC J 等通过研究验证了圆筒型FPSO 的运动性能可适应钢悬链立管(SCR)在深水油田的应用。
本文以中国南海某深水油气田开发为研究对象,采用深吃水的圆筒型FPSO 改善其运动性能,以在该油气田的开发中适应钢悬链立管的设计和应用需求,降低立管的工程投资。此研究将基于三维势流理论和莫里森(Morison)方程,采用Sesam系列软件建立圆筒型FPSO 水动力计算模型,并进行水动力计算,研究分析圆筒型FPSO 的船体直径、阻尼板直径、吃水等变化对其运动性能的影响,为深水油气田开发前期研究设计中浮式装置总体设计和立管的选型提供参考和指导。
1 计算分析原理和方法
本文所研究的圆筒型FPSO 船体及阻尼板相当于大尺度结构物,采用三维势流理论计算其所受的绕射力和惯性力等作用。阻尼板的黏性阻尼贡献需采用莫里森模型求解。通过建立基于三维势流理论的面元模型与莫里森模型组合成的混合模型可以较好地解决此类结构物的水动力分析问题。本文研究首先分别建立圆筒型FPSO 的面元模型和阻尼板的莫里森模型,然后组合成水动力分析混合模型,再进行水动力计算,最后进行运动响应计算结果的后处理。计算分析流程如图1 所示。
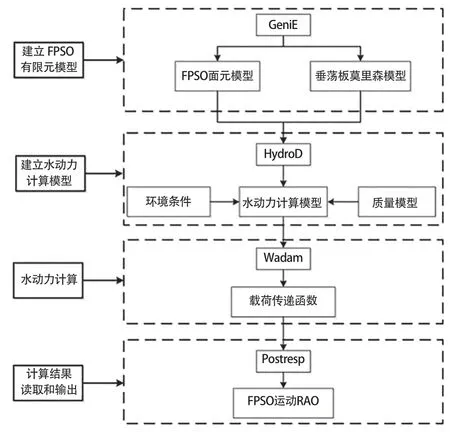
图1 圆筒型FPSO 水动力计算流程
2 计算模型与环境数据
2.1 有限元模型
采用面单元模型计算基于三维势流理论的动压力、附加质量和阻尼。在Sesam-GeniE 中建立圆筒型FPSO 的几何模型和湿表面有限元模型如图2 所示。圆筒型FPSO 有限元模型全部采用四边形网格,网格尺寸约2 m,整个模型网格节点数量约 8 161 个,单元数量约8 100 个。船体外表面设置由流体指向船体表面的静水压力面,即湿表面。

图2 圆筒型FPSO 船体面元模型
本文采用莫里森模型计算阻尼板的拖曳力,在Sesam-Genie 软件中采用杆单元建立二维莫里森模型,建模时为了防止莫里森模型的浮力及F-K力(傅汝德-克雷洛夫力)对水动力分析结果的影响,莫里森模型的直径必须很小(Re~10)。本文中莫里森模型的直径为0.01 m,整个莫里森模型的单元和节点数均为158 个,如图3 所示。

图3 阻尼板莫里森有限元模型
2.2 水动力分析模型
水动力计算时,将圆筒型FPSO 船体面元有限元模型和阻尼板莫里森有限元模型导入Sesam 的HydroD 软件中,设置环境参数、莫里森模型的附加质量系数和阻尼系数以及质量模型等。水动力计算分析模型如图4 所示。

图4 圆筒型FPSO 水动力分析模型
2.3 环境条件数据
水动力计算时,浪向角取0~180°、间隔15°,共13 个浪向。波浪周期取2~40 s,其中:2~10 s 间隔1 s、10~24 s 间隔0.5 s、24~40 s 间隔2 s,共45个波浪周期。水深为1 450 m。采用JONSWAP 谱定义不规则波,其谱密度函数表达式为:


考虑到黏性阻尼的非线性作用将导致不同海况下的RAO 不同,而且这种影响对圆筒型FPSO 的垂荡运动尤为明显,因此本文中将分别对圆筒型FPSO在一年一遇、十年一遇、百年一遇以及千年一遇环境条件数据下的运动响应进行分析。南海某深水油气田海域的波浪主极值数据见表1。

表1 波浪主极值数据
3 圆筒型FPSO 与船型FPSO 运动响应对比分析
为本文选取南海载重量相近的船型FPSO 和圆筒型FPSO 进行运动响应的对比分析,船型FPSO与圆筒型FPSO 主尺度如表2 所示。
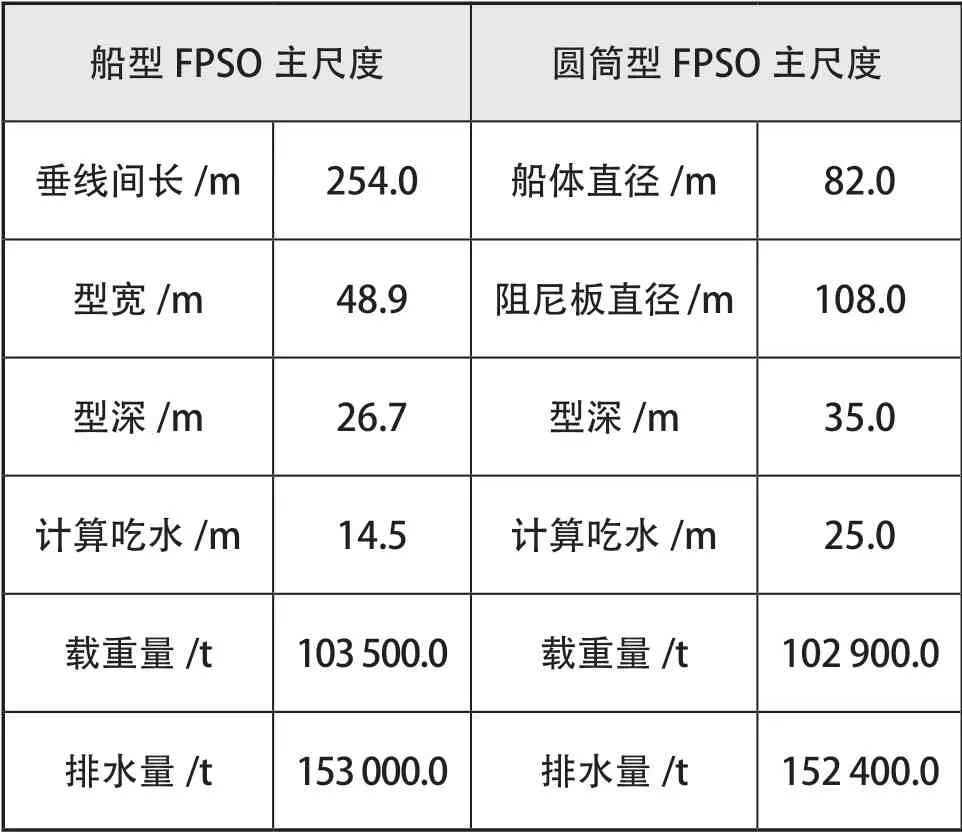
表2 船型FPSO 和圆筒型FPSO 主尺度参数
通过计算分析得圆筒型FPSO 与船型FPSO 纵摇、横摇和垂荡运动RAO 对比曲线分别如图5 和图6 所示,运动幅值与固有周期对比见下页表3。
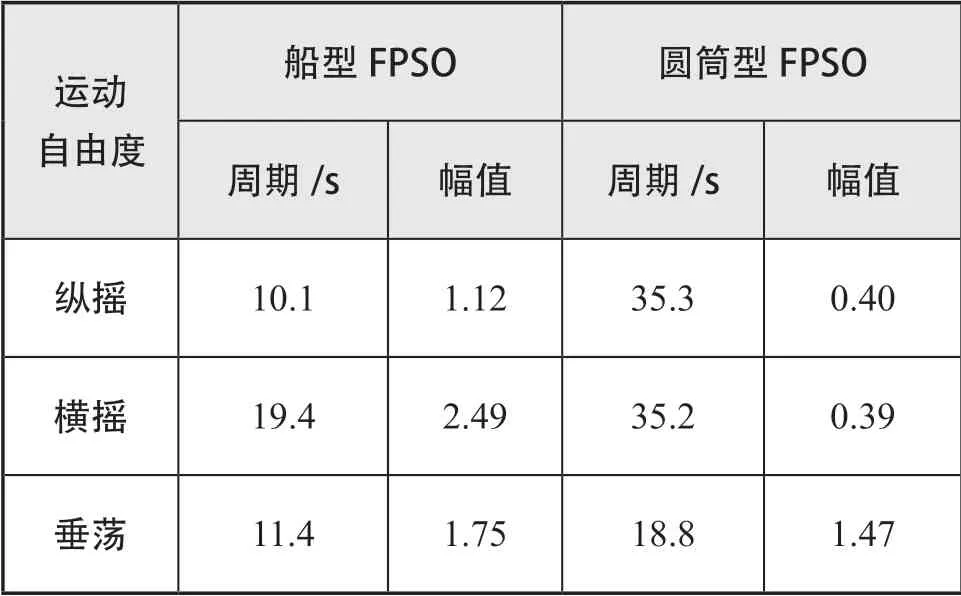
表3 船型FPSO 和圆筒型FPSO 运动RAO幅值与固有周期对比

图5 圆筒型FPSO 与船型FPSO 横/纵摇运动RAO 对比曲线
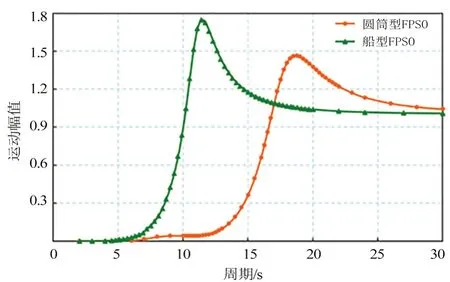
图6 圆筒型FPSO 与船型FPSO 垂荡运动RAO 对比曲线
从图5~6 及表3 中可以看出,圆筒型FPSO 横摇/纵摇运动RAO 幅值要比传统船型FPSO 的RAO幅值小很多,运动固有周期更大,更有利于提高FPSO 船体使用寿命。圆筒型FPSO 垂荡运动RAO幅值同样比船型FPSO 垂荡运动RAO 幅值小,而且圆筒型FPSO 垂荡固有周期要比船型FPSO 大,更有利于深水立管的设计。
4 圆筒型FPSO 垂荡运动响应敏感性分析
考虑到圆筒型FPSO 的垂荡运动响应对其能否在深水油气田中应用SCR 至关重要,本文将主要对船体直径、吃水、阻尼板直径等对圆筒型FPSO垂荡运动响应的影响进行分析。
4.1 船体直径影响分析
选取船体直径不同的4 种尺度圆筒型FPSO分别进行水动力计算,以研究船体直径对圆筒型FPSO 垂荡运动性能的影响,圆筒型FPSO 的主尺度如表4 所示。
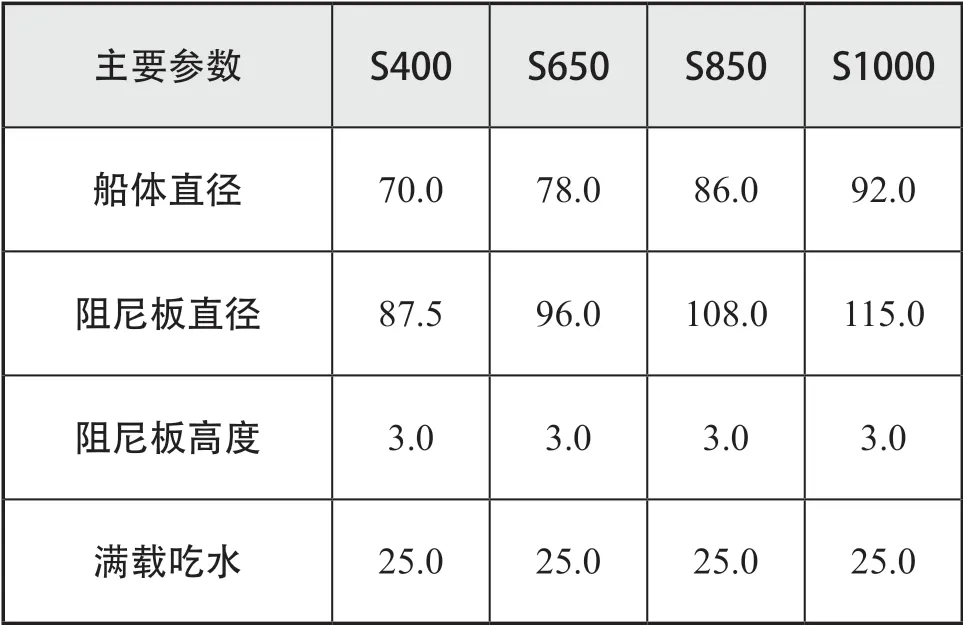
表4 不同圆筒型FPSO 主尺度参数m
不同船体直径圆筒型FPSO 垂荡运动RAO 曲线如图7 所示。对比图中曲线可知,随着船体直径的不断增大,船体垂荡固有周期逐渐增加,可更好地与波浪周期错开,且垂荡运动性能逐渐得到改善。
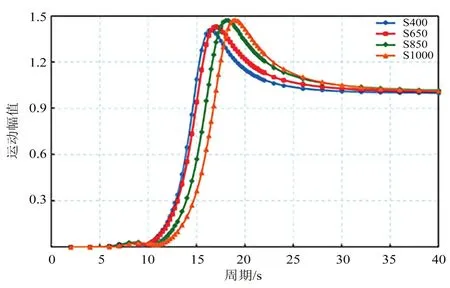
图7 不同船体直径圆筒型FPSO 垂荡运动RAO 曲线
4.2 阻尼板直径影响分析
基于76 m 船体直径的圆筒型FPSO,分别对阻尼板直径为110 m、112 m和114 m的圆筒型FPSO进行水动力计算,得到不同阻尼板直径下的圆筒型FPSO 垂荡运动RAO 曲线如图8 所示,垂荡运动周期如表5 所示。

图8 不同阻尼板直径圆筒型FPSO 垂荡运动RAO 曲线

表5 不同阻尼板直径圆筒型FPSO 垂荡运动固有周期
从图8 和表5 可以看出:随着圆筒型FPSO 阻尼板直径的增加,船体垂荡运动RAO 最大幅值变化不大,但垂荡运动固有周期随着阻尼板直径的增加逐渐增大,可更好地避开波浪周期,更有利于SCR 的强度设计。然而,随着阻尼板直径的增加,靠近波浪谱峰周期附近的运动幅值也有微幅增加,不利于SCR 的疲劳设计。
4.3 船体吃水影响
针对船体直径为76 m、阻尼板直径为114 m的圆筒型FPSO,分别对其船体吃水为25 m、30 m、35 m 时进行水动力计算,得到不同吃水下的圆筒型FPSO 垂荡运动RAO 曲线如图9 所示。
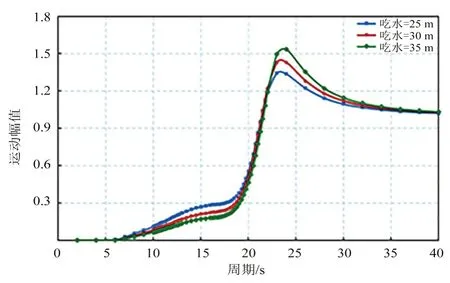
图9 不同吃水圆筒型FPSO 垂荡运动RAO 曲线
从图9 可以看出,随着圆筒型FPSO 吃水从 25 m 增加至35 m,垂荡运动固有周期增加幅度很小,但在波浪谱峰周期(T=16.3 s)附近的RAO幅值会降低,有利于改善SCR 的疲劳性能。
4.4 环境条件重现期影响
针对南海某深水油气田项目圆筒型FPSO 的主尺度,对其在一年一遇、十年一遇、百年一遇和千年一遇环境条件下的运动性能进行分析,得到圆筒型FPSO 的纵荡/横荡、纵摇/横摇、垂荡运动RAO 曲线分别如图10~12 所示。
从图10~12可以看出:不同重现期环境条件下,圆筒型FPSO 纵荡/横荡和纵摇/横摇运动的RAO几乎相同,但由于黏性阻尼的非线性作用而导致垂荡运动RAO 曲线差异较大,垂向运动幅值随着重现期增加而减小。
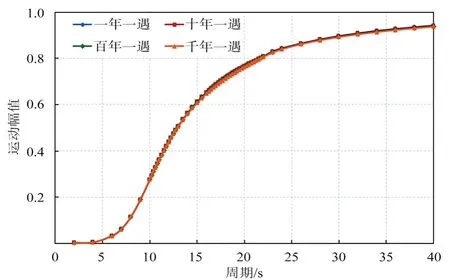
图10 圆筒型FPSO 纵荡/横荡运动RAO 曲线
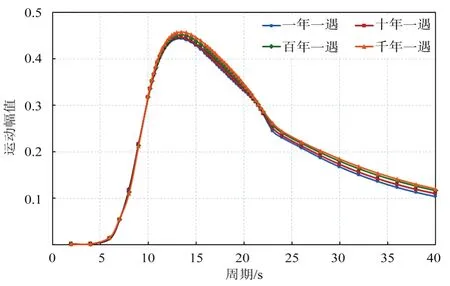
图11 圆筒型FPSO 纵摇/横摇运动RAO 曲线

图12 圆筒型FPSO 垂荡运动RAO 曲线
5 结 论
本文基于三维势流理论及莫里森方程,采用Sesam 系列软件对圆筒型FPSO 进行水动力分析,并针对南海某深水油气田开发项目,对圆筒型FPSO 在波浪中的运动响应特性进行了系统分析,得出主要结论如下:
(1)相比于相近载重量的船型FPSO,深吃水圆筒型FPSO 的垂荡运动响应小,固有周期远离波浪主要能量范围,更有利于在深水油气田开发中应用钢悬链立管(SCR)。
(2)圆筒型FPSO 船体直径增大,垂荡运动固有周期随之增加,可更好地与波浪谱峰周期错开,使其垂荡运动性能逐渐得到改善。
(3)圆筒型FPSO 阻尼板直径增大,垂荡运动固有周期将随之增加,有利于SCR 的强度设计,但对SCR 的疲劳设计会产生一定不利影响。
(4)增加圆筒型FPSO 的吃水,垂荡运动固有周期增加幅度很小,但在波浪谱峰周期附近的垂荡运动幅值会降低,有利于改善SCR 的疲劳。
(5)黏性阻尼的非线性作用导致圆筒型FPSO垂向运动RAO 幅值随着环境条件重现期增加而减小。
