基于目标规划的企业产销算法模型研究及其应用
2022-05-02黄如兵
黄如兵,田 凯
(1.安徽职业技术学院,安徽 合肥 230011;2. 长鑫存储技术有限公司,安徽 合肥 230009 )
0 引言
在市场竞争激烈,市场需求关系变化急剧的情况下[1],掌握科学的经营决策方法,将有效规避经营风险,为企业带来最大的经济利益,对企业的生存和发展具有十分重要的意义[2].制造型企业的业务主要有:研发设计、采购原材料、生产加工、仓储物流及产品销售[3].基于目标规划的模型已广泛应用于社会生产生活的各个领域,常采用网络流算法、列生成算法、遗传算法及邻域搜索等算法求解规划模型[4],这些算法都是指数级的,且主要通过建立单目标规划模型求解[5-6],在多目标场景中使用效果不好.本文结合生产实际中的约束条件,采用了非线性单一目标规划,建立了公司利润最大算法模型,通过引入公司利润和营销部利润权重系数,运用非线性多目标规划的方法,建立了公司与营销部利益均衡化算法模型,综合考虑公司利润与营销部利润均衡化关系,构建应用模型,便于企业做出最有益于企业生产与销售决策.
某企业下设营销部,企业产品通过公司的营销部对外销售.在企业生产能力的限制和制约下,企业需要综合考虑公司利润与生产能力,制定生产与销售决策,公司生产首先要对已签定合同的订单安排生产,同时要兼顾意向签约订单进行有计划的安排生产.一方面,企业生产要供应已签约的销售订单合同;另一方面,企业要激励营销部门与意向签约客户达成合作,签订正式订单合同.对于已签约销售合同和意向签约量,企业根据销售量向营销部发放经费(包括工资以及宣传费用等).此外,企业还希望销售部门努力再多销售一些计划外产品.对于计划外销售的产品,实行承包制,营销部向企业缴纳利润.产品的生产费用由企业承担,与销售有关的费用(如产品的宣传费用等)由营销部承担.本文研究在该模式下企业的产品生产、销售模型.
1 公司利润最大化模型
分析公司利润组成可知,其分为两部分[7]:计划内产品所获得利润和营销部向公司上交的计划外产品利润.其中,计划内的已签约产品是公司必须安排生产的部分,意向签约产品和计划外签约产品是公司根据需要选择生产的部分.公司的利润可以表述为
公司利润=销售额-成本-销售产品的经费+营销部上缴的利润.
1.1 模型假设
(1)销售部作为公司一个下属机构的同时,又是一个独立的利益团体;
(2)产品的生产成本中,包括原材料、辅助材料、制造费用和公司人员工资等费用;
(3)各意向客户签订合同是独立事件;
(4)已签约合同必须履行;
(5)产销平衡,无库存.
1.2 符号说明
Mj:第j类产品的年实际生产量,单位:万个;
Hi:第i种产品的年实际生产量,单位:万个;
Qa(i):第i种产品的已签约量,单位:万个;
qa(i,l):第l个已签约客户,对第i种产品的签约量,单位:万个;
Qb(i):第i种产品的意向签约量,单位:万个;
qb(i,m):第m个意向签约客户,对第i种产品的签约量,单位:万个;
Qc(i):第i种产品的计划外签约量,单位:万个;
xi:第i种产品,计划内的产量,单位:万个;
yi:第i种产品,计划外的产量,单位:万个;
α(Hi):第i种产品,生产量为Hi时的成本,单位:万元;
β(xi):第i种产品,计划内销售量为xi时的销售经费,单位:万元;
γ(qa(i,l)):第i种产品,销售量为qa(i,l)时的销售额,单位:万元;
g(yi):第i种产品,计划外销售量为yi时营销部向公司缴纳的利润,单位:万元;
E(Qa(i),Qb(i)):第i种产品,已签约量为Qa(i)、意向签约量为Qb(i)时的销售额,单位:万元;
D(xi,yi):第i种产品,计划内生产量xi、计划外生产量为yi时的成本,单位:万元.
1.3 公司利润最大化模型构建
计划内产品销售额由已签约产品和意向签约产品两部分销售额组成,其数学表达式如下:
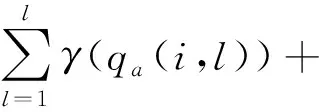
(1)
产品的总生产成本由计划内和计划外两部分产品的成本组成,其数学表达式如下:
D(xi,yi)=α(xi+yi).
(2)
公司的利润表达式为
(3)
将(1)、(2)代入(3)得公司利润最大化模型:
(4)
公式(4)中各函数的表达式如下:
α(xi+yi)=
Aα(i)(xi+yi)3+Bα(i)(xi+yi)2+
Cα(i)(xi+yi)+Dα(i),
(5)
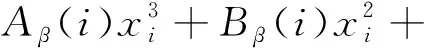
(6)
γ(qa(i,l))=
Aγ(i)qa(i,l)3+Bγ(i)qa(i,l)2+
Cγ(i)qa(i,l)+Dγ(i),
(7)
(8)
公式(5)(6)(7)和(8)中,变量Aα(i)、Aβ(i)、Aγ(i)、Ag(i)分别表示成本函数、销售产品经费函数、销售额函数和上缴给公司利润函数的各项系数.
模型中各函数变量关系约束如下:
(9)
2 公司与营销部利润均衡化模型
产品销售所获得的总利润等于公司利润与销售部利润之和.公司利润最大化与营销部利润最大化是彼此对立的.对于两者利益的兼顾问题,可以通过设定其获得利润占总利润的比例来解决.根据公司利润的关系式,营销部的利润可由营销部的收入减去其支出得到.营销部利润可以表述为
营销部利润=营销部收入-计划内销售费用-计划外上缴利润-计划外宣传费用.
2.1 模型假设
(1)计划外销售的产品也需要宣传费用,且由宣传部承担;
(2)销售部利润不超过总利润40%.
2.2 符号说明
η(xi):第i种产品,销售量xi为时的宣传费用,单位:万元;
Rg:公司利润;
Ry:营销部利润;
σg:公司利润占产品销售总利润的比例;
σg:营销部利润占产品销售总利润的比例.
2.3 公司与营销部利润均衡化模型建立
由公司利润最大化模型可知,公司利润表达式为
(10)
结合问题2,得到营销部利润表达式:
(11)
建立公司、营销部利益均衡化模型:
(12)
(13)
模型参数约束如下:
(14)
3 算例分析
某电器公司2021年计划生产3类10种产品,其中包括:热水壶(1.5升,1.8升,2升)、豆浆机(0.9升,1.1升,1.3升)、电饭煲(2升,2.5升,3升,3.5升).
3类产品的年最大生产能力分别为:
热水壶:5万个;豆浆机:6.5万个;电饭煲6.2万个.
请分别按照以使公司的利润达到最大和兼顾公司和营销部二者的利益分别为该电器公司制定相应的生产、销售计划.
3.1 公司利润最大化产销方案
已签约产品的签约量约束
(15)
意向签约产品的签约量约束
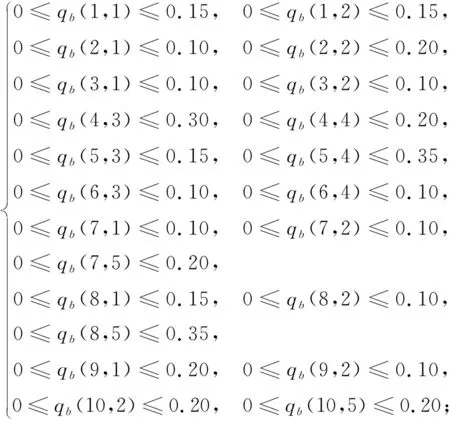
(16)
计划外签约产品的签约量约束
(17)
3类产品年生产能力约束
(18)
使用Matlab软件对生产成本与生产量关系数据进行函数拟合,其各项系数计算结果见表1所列.
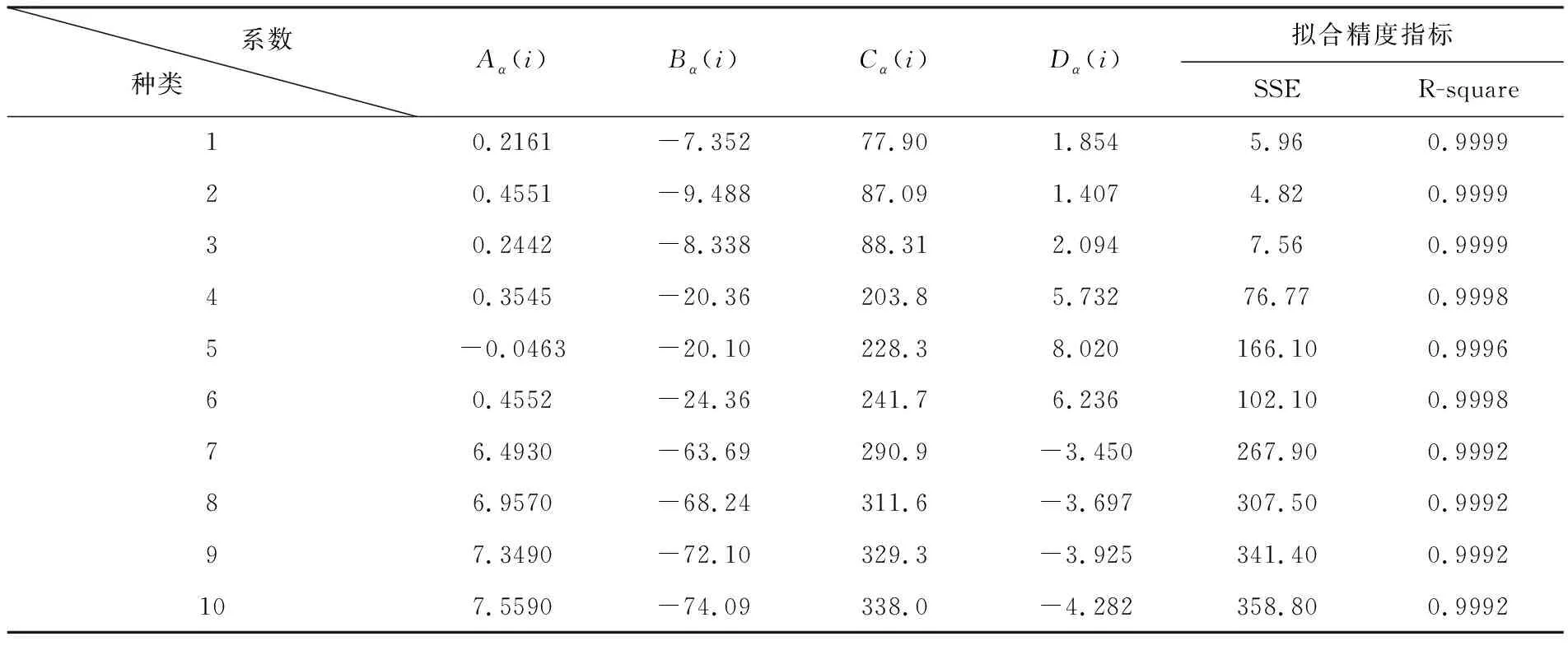
表1 成本函数系数表
对销售额与销售量关系数据进行函数拟合,所得各项系数计算结果见表2所列.
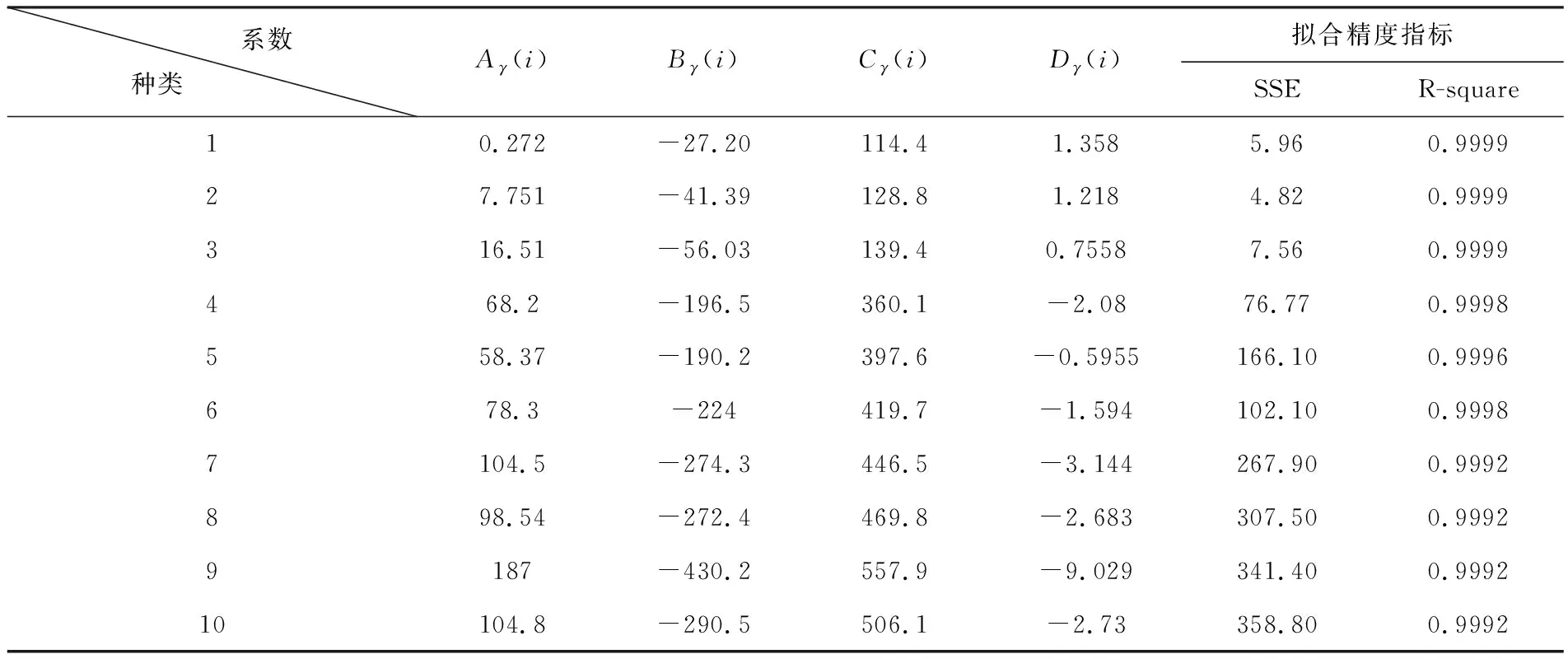
表2 销售额函数系数表
对销售经费与销售量数据进行函数拟合,β(xi)各项系数计算结果见表3所列.
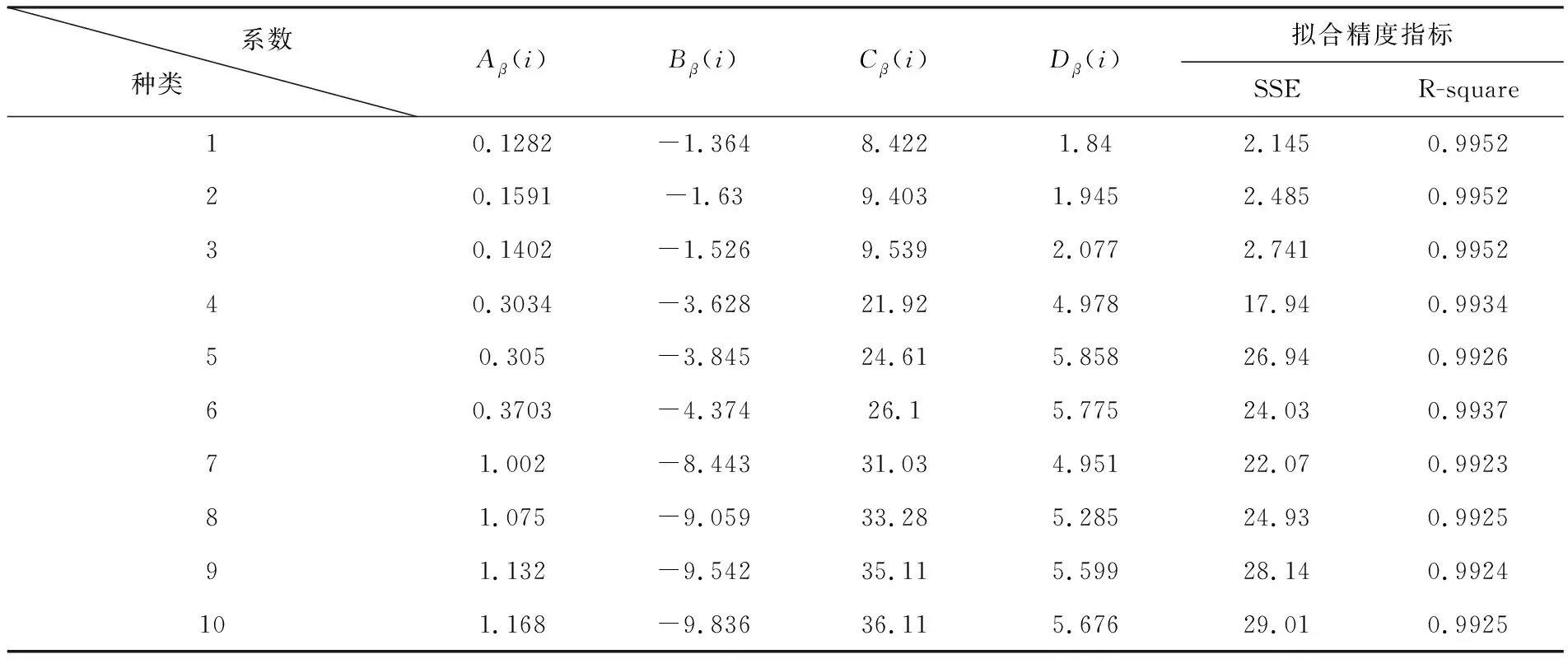
表3 销售产品的经费函数系数表
对营销部缴纳的利润与销售量数据进行函数拟合,g(yi)各项系数计算结果见表4所列.
根据已经建立的公司利润最大化模型,及有关拟合函数,运用Lingo软件对模型进行求解[8],得到公司利润最大时的产销方案,详见表5.
方案结果分析:
(1)公司利润最大时,计划外的签约量为零,这说明计划外销售的产品并不能增加公司的利润(但并不是说销售的产品不能产生利润),其销售所得的利润流向了营销部;进一步分析可以看出,随着生产、销售规模的扩大,公司会逐渐从计划外销售的产品中获得利润.这些规律在题目的表2、表4和表5中,也可得具体的体现.
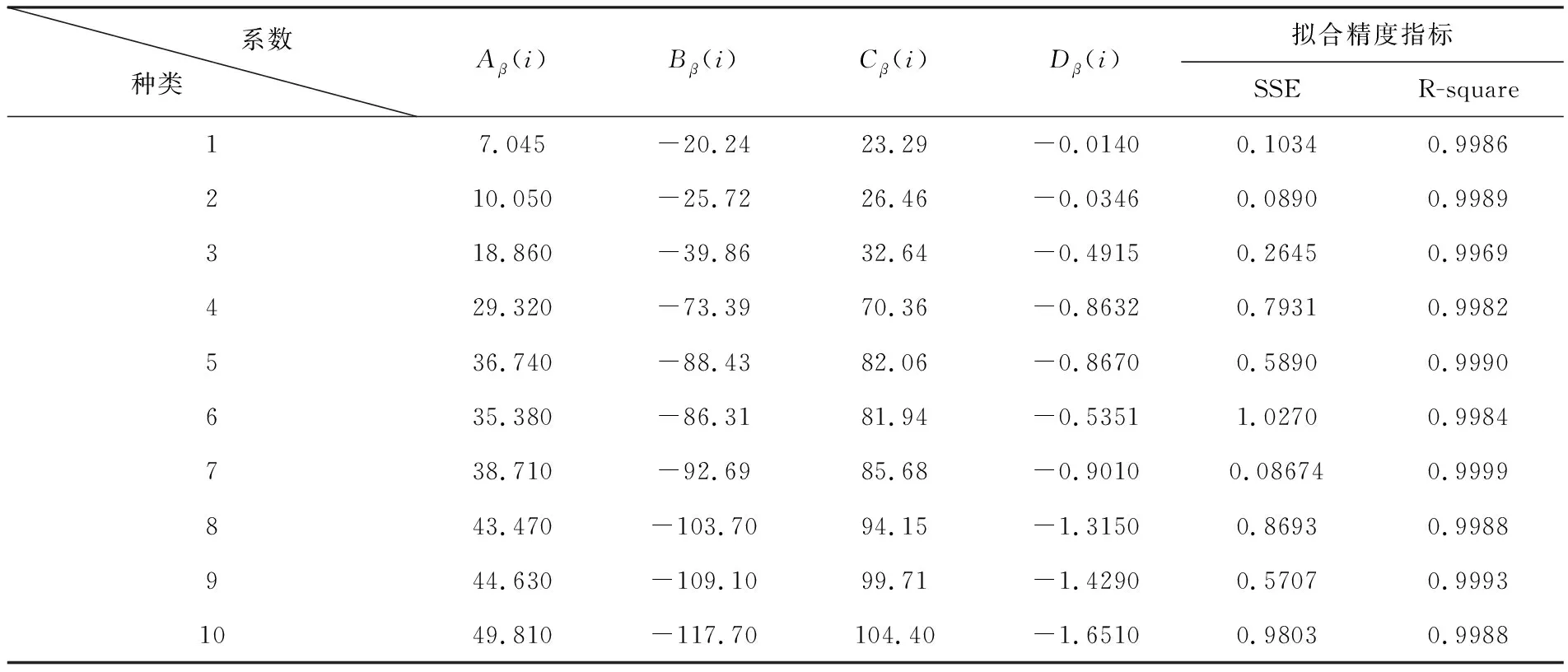
表4 营销部缴纳的利润与销售量函数系数表
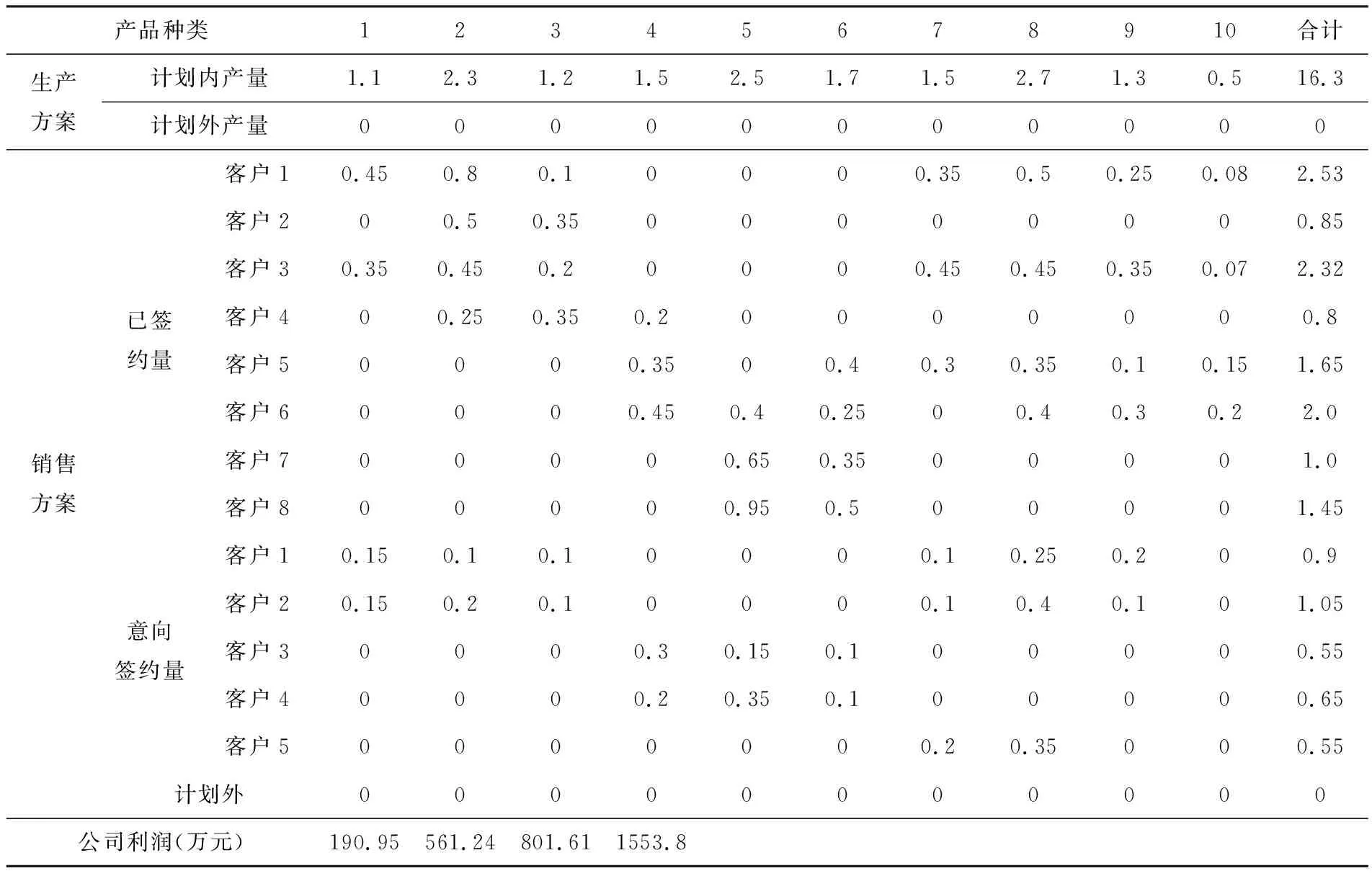
表5 公司利润最大时的产销方案 单位:万件
(2)计划内部分,公司并不是对所有种类产品都按最大生产能力进行生产,这说明部分产品在一定的生产规模内,公司存在“亏本”的可能.
3.2 公司与营销部利益均衡化产销方案
使用Matlab软件对宣传费用与销售量关系数据进行函数拟合,各项系数计算结果见表6所列.
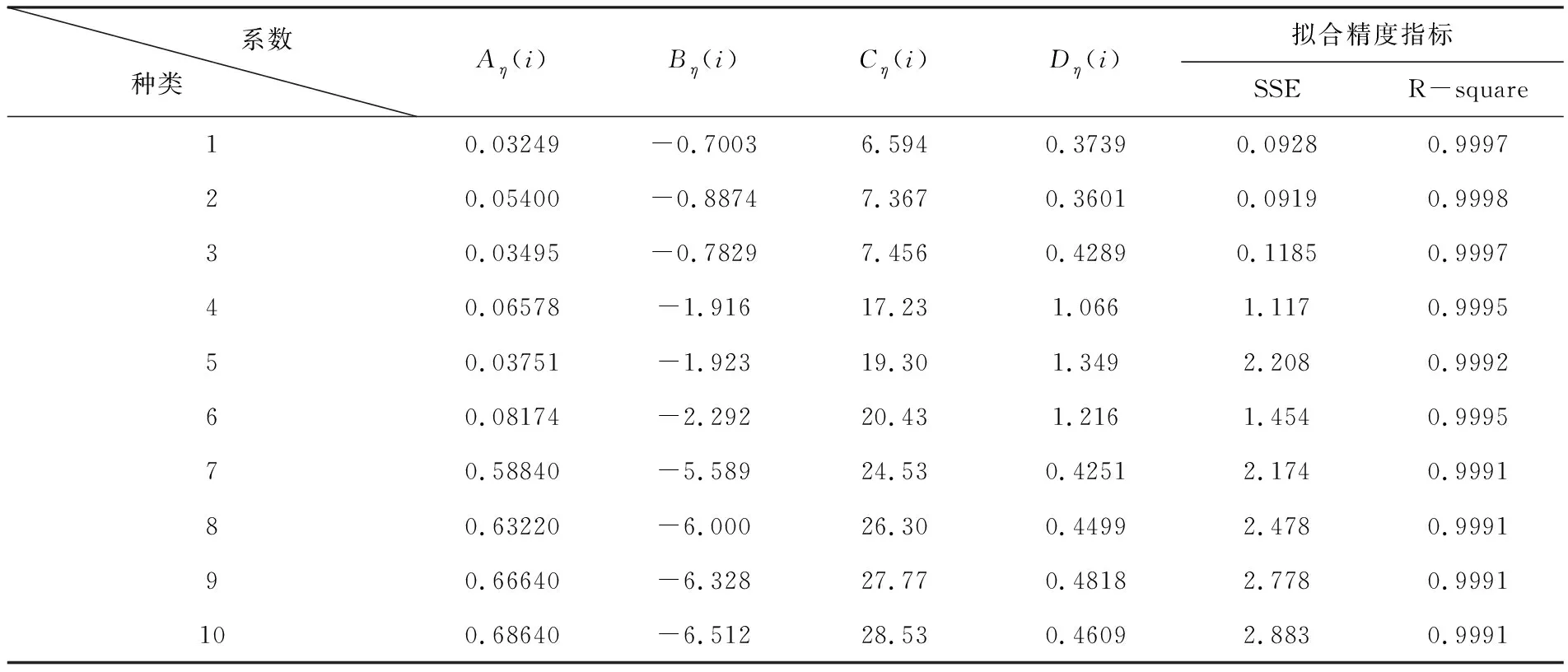
表6 宣传费用函数系数表
运用Lingo软件对模型进行求解,得到营销部利润占产品利润15%的产销方案,详见表7所列.
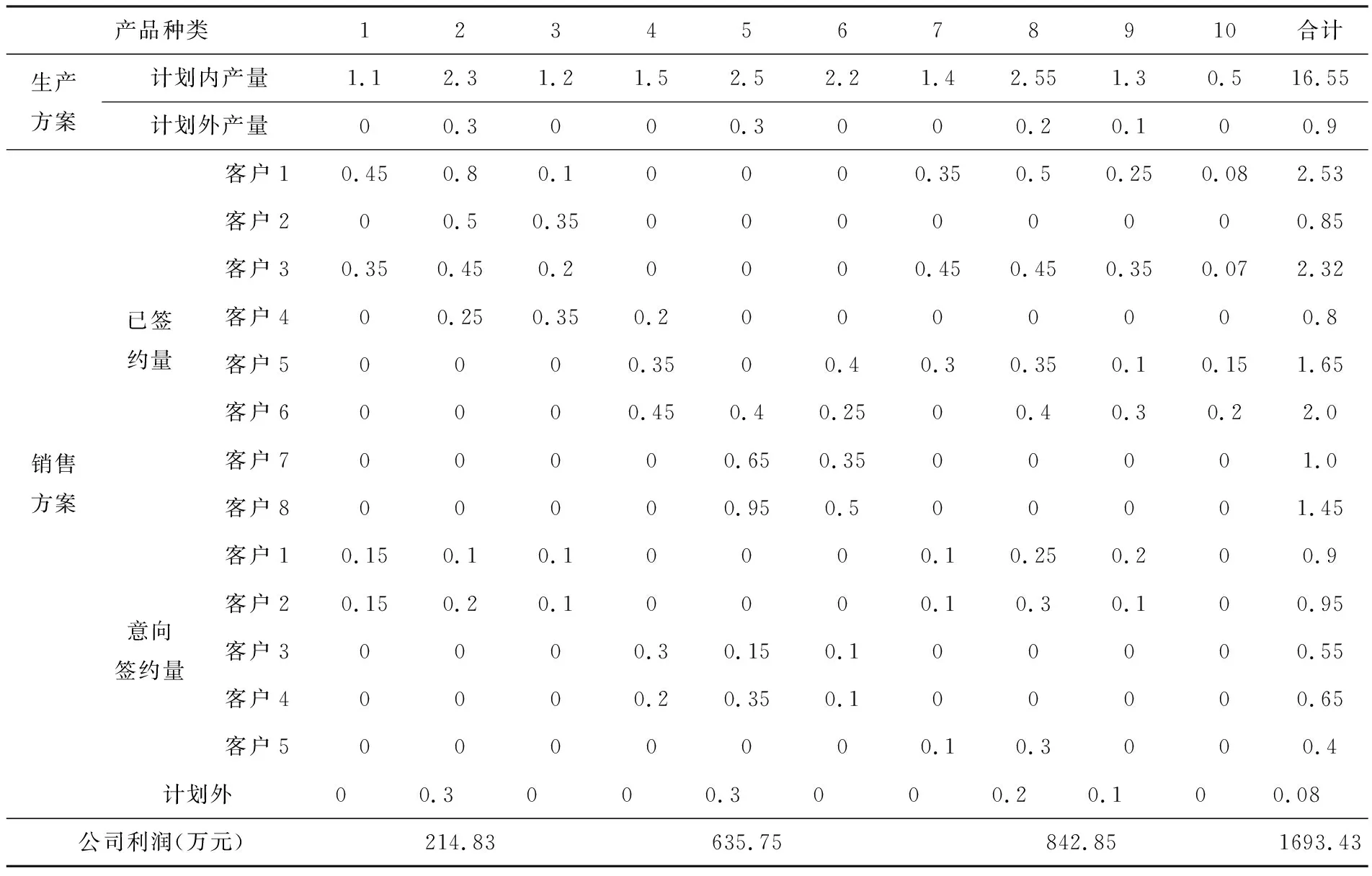
表7 销售部利润占产品总利润15%时的产销方案 单位:万件
运用Lingo软件对模型进行求解,得到营销部利润占产品利润25%的产销方案,详见表8所列.
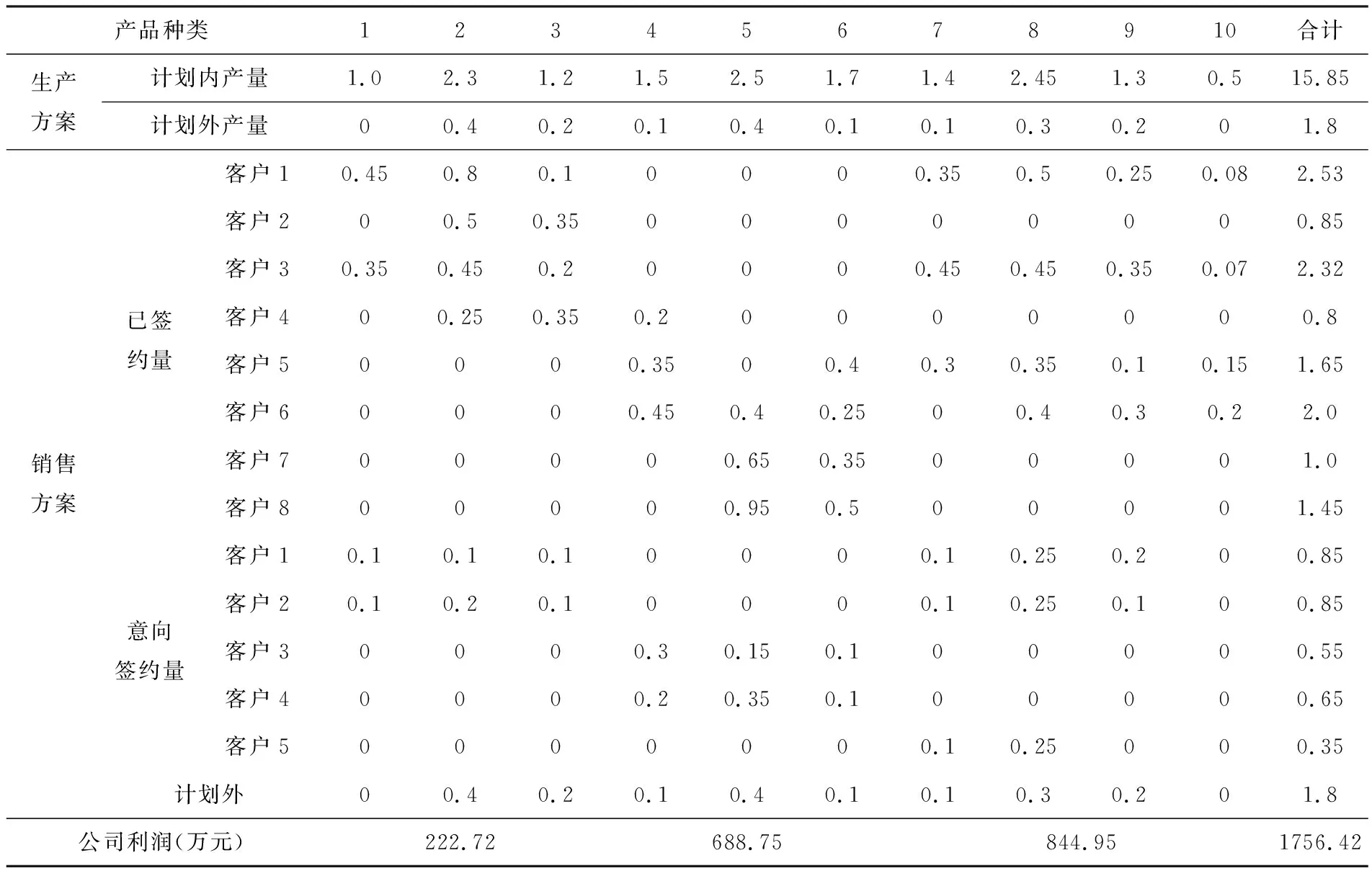
表8 销售部利润占产品总利润25%时的产销方案 单位:万件
方案结果分析:
(1)随着模型中设置的营销部利润比例从10%上升到25%,产品的总利润在不断增加.
(2)在不设置营销部利润占产品总利润,且只追求产品销售利润最大时,可以得到总利润约为1790.18万元,此时营销部和公司的利润比例大约在3:7.
4 总结与改进
本文通过研究HY电器公司2021年相关数据,利用非线性规划中的单一目标规划方案与多目标规划方案分别制定了满足不同要求下的生产、销售方案,不仅实现了公司利润最大化以及营销部总收入极大化,同时兼顾了客户利益,达到了均衡销售.
采用运筹学中的非线性目标规划方法,克服了线性规划方法目标函数单一、约束条件苛刻、无法解决矛盾条件下的规划问题等缺点.在多目标规划的目标函数中,使用目标优先级系数,恰好解决了公司、销售部和客户利益均衡的问题.文章基于目标规划构建的算法模型,通过实际算例分析验证,求得模型最优方案,有益于企业的生产与销售决策.
