恰有12个极大子群的有限幂零群
2022-05-02胡玲玲何立国
胡玲玲,何立国
(沈阳工业大学 理学院,辽宁 沈阳 110870)
0 引言
有限幂零群是群论的一类十分重要的群.极大子群在有限幂零群的研究中有着非常重要的作用.有限幂零群的极大子群的数量性质能够反映出该群的许多性质.如文献[1]刻画了极大子群的个数小于5的有限群的结构;文献[2]研究了恰有5个极大子群的有限幂零群、非幂零群的群结构;文献[5]刻画了恰有9和10个极大子群的有限幂零群的群结构;文献[6]刻画了恰有11个极大子群的有限幂零群的群结构.本文继文献[5-6]的工作,对恰有12个极大子群的有限幂零群的结构进行刻画.
1 相关引理
引理1[6]不存在恰有2个极大子群的p-群.即非循环p-群的极大子群个数至少为3.
引理2[6]群G恰有一个极大子群的充要条件是:G为素数幂阶循环群.
引理3[5]设G是有限p-群,且
|G/φ(G)|=pd,
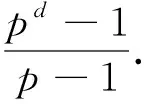
特别地,若G非循环,则p=2时,G的极大子群的个数至少为3;当p>2时,G的极大子群的个数至少为4.
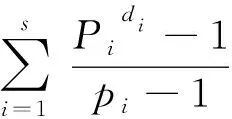
2 主要结果
定理设G是有限幂零群,则G恰有12个极大子群的充要条件是G是下列情形之一:
(1)G=P1×P2×P3×P4×P5×P6×P7×P8×P9×P10×P11×P12,其中Pi∈Sylpi(G),且为不同素数幂阶循环群.
(2)G=P1×P2×P3×P4×P5×P6×P7×P8×P9×P10,其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2,P3,P4,P5,P6,P7,P8,P9,P10为不同素数幂阶循环群.
(3)G=P1×P2×P3×P4×P5×P6×P7×P8×P9,其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2,P3,P4,P5,P6,P7,P8,P9为不同素数幂阶循环群.
(4)G=P1×P2×P3×P4×P5×P6×P7,其中Pi∈Sylpi(G),且P1为2元生成的5-群,P2,P3,P4,P5,P6,P7为不同素数幂阶循环群.
(5)G=P1×P2×P3×P4×P5×P6×P7,其中Pi∈Sylpi(G),且P1为5元生成的2-群,P2为2元生成的3-群,P3,P4,P5,P6,P7为不同素数幂阶循环群.
(6)G=P1×P2×P3×P4×P5×P6,其中Pi∈Sylpi(G),且P1为3元生成的2-群,P2,P3,P4,P5,P6为不同素数幂阶循环群.
(7)G=P1×P2×P3×P4×P5,其中Pi∈Sylpi(G),且P1为2元生成的7-群,P2,P3,P4,P5为不同素数幂阶循环群.
(8)G=P1×P2×P3×P4×P5,其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2为2元生成的5-群,P3,P4,P5为不同素数幂阶循环群.
(9)G=P1×P2×P3×P4, 其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2为2元生成的5-群,P3,P4为不同素数幂阶循环群.
(10)G=P1×P2×P3, 其中Pi∈Sylpi(G),且P1为2元生成的9-群,P2,P3为不同素数幂阶循环群.
(11)G=P1×P2×P3, 其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2为2元生成的7-群,P3为素数幂阶循环群.
(12)G=P1×P2×P3, 其中Pi∈Sylpi(G),且P1为3元生成的2-群,P2为2元生成的3-群,P3为素数幂阶循环群.
(13)G=P1×P2, 其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2为2元生成的7-群.
(14)G=P1, 其中P1∈Sylp1(G),且为2元生成11-群.
证明先证充分性.
已知G是有限幂零群,证明当G是上述14种情况时,G有12个极大子群.
当G是情况(1)时,由于Pi(i=1,2,…,12)是素数幂阶循环群,由引理2可知Pi(i=1,2,…,12)恰有一个极大子群,从而由引理4可知G有
个极大子群.
当G是情况(2)时,由于P1是2元生成的2-群,故由引理3可知P1极大子群的个数为
又由于Pi(i=2,…,12)为素数幂阶循环群,故由引理2可知Pi(i=1,2,…,12)恰有一个极大子群,从而G有
个极大子群.当G是余下的12种情况时,类似情况(2)的证明可得G有12个极大子群.
下证必要性.
已知有限幂零群G恰有12个极大子群,证明G必为上述14种情况之一.
由于G是幂零群,所以G=P1×P2×…×Ps,其中Pi∈Sylpi(G),p1 (1)当s=12,由引理4可知 从而Pi(i=1,2,3,…,12)恰有一个极大子群.又由引理2可知Pi为不同素数幂阶的循环群. 综上可知,当s=12时,G=P1×P2×P3×P4×P5×P6×P7×P8×P9×P10×P11×P12,其中Pi∈Sylpi(G),且为不同素数幂阶循环群. (2)当s=11时,由引理4可知至少存在一个di≥2.不妨假定d1≥2,于是P1是非循环群.又由引理3和引理1可知P1至少存在3个极大子群,从而由引理4可知G至少存在13个极大子群,矛盾. 综上当s=10时,G=P1×P2×P3×P4×P5×P6×P7×P8×P9×P10,其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2,P3,P4,P5,P6,P7,P8,P9,P10为不同素数幂阶循环群. (4)当s=9时,若只有d1≥2,即P1有4个极大子群,由引理3可得等式 从而p1=3,d1=2,故P1为2元生成的3-群.若d1≥2,d2≥2,由引理1和引理3可知P1,P2各至少有3个极大子群,即G至少有13个极大子群,矛盾. 综上当s=9时,G=P1×P2×P3×P4×P5×P6×P7×P8×P9,其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2,P3,P4,P5,P6,P7,P8,P9为不同素数幂阶循环群. (5)当s=8时,若只有d1≥2,即P1有5个极大子群,由引理3可知, 而此时没有符合条件的值使之成立.若d1≥2,d2≥2,即P1,P2共有6个极大子群,故由引理3可知 由等式可得p1=p2=2,与p1≠p2矛盾. (6)当s=7时,若只有d1≥2,由 可得p1=5,d1=2,故P1为2元生成的5-群.若d1≥2,d2≥2,由 可得p1=2,d1=5,p2=3,d2=2,从而P1为5元生成的2-群,P2为2元生成的3-群. 综上,当s=7时G有两种情况,分别为: G=P1×P2×P3×P4×P5×P6×P7,其中Pi∈Sylpi(G),且P1为2元生成的5-群,P2,P3,P4,P5,P6,P7为不同素数幂阶循环群. G=P1×P2×P3×P4×P5×P6×P7,其中Pi∈Sylpi(G),且P1为5元生成的2-群,P2为2元生成的3-群,P3,P4,P5,P6,P7为不同素数幂阶循环群. (7)当s=6时,若只有d1≥2,由等式 可推得p1=2,d1=3,故P1为3元生成的2-群.若d1≥2,d2≥2,由 和p1 综上,当s=6时,G=P1×P2×P3×P4×P5×P6,其中Pi∈Sylpi(G),且P1为3元生成的2-群,P2,P3,P4,P5,P6为不同素数幂阶循环群. (8)当s=5时,若只有d1≥2,则由等式 可知p1=7,d1=2,故P1为2元生成7-群.若d1≥2,d2≥2,由 可得p1=2,d1=2,p2=5,d2=2,故P1为2元生成的2-群,P2为2元生成的5-群. 综上,当s=5时,G有两种情况,分别为: G=P1×P2×P3×P4×P5,其中Pi∈Sylpi(G),且P1为2元生成的7-群,P2,P3,P4,P5为不同素数幂阶循环群. G=P1×P2×P3×P4×P5,其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2为2元生成的5-群,P3,P4,P5为不同素数幂阶循环群. (9)当s=4时,若只有d1≥2,即P1有9个极大子群,故 但经过计算可知没有满足条件的值使之成立.若d1≥2,d2≥2,由等式 可得p1=2,d1=3,p2=2,d2=3,或p1=3,d1=2,p2=5,d2=2.又由于p1 且p1 综上当s=4时,G=P1×P2×P3×P4,其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2为2元生成的5-群,P3,P4为不同素数幂阶循环群. (10)当s=3时,若只有d1≥2,由 可知p1=9,d1=2,故P1是2元生成9-群.若d1≥2,d2≥2,由等式 可知p1=2,d1=2,p2=7,d2=2,故P1是2元生成2-群,P2为2元生成的7-群,或p1=2,d1=3,p2=3,d2=2,故P1是3元生成2-群,P2为2元生成的3-群.若d1≥2,d2≥2,d3≥2,由 且p1 综上,当s=3时,G有三种情况,分别为: G=P1×P2×P3,其中Pi∈Sylpi(G),且P1为2元生成的9-群,P2,P3为不同素数幂阶循环群. G=P1×P2×P3,其中Pi∈Sylpi(G),且P1为2元生成的2-群,P2为2元生成的7-群,P3为素数幂阶循环群. G=P1×P2×P3,其中Pi∈Sylpi(G),且P1为3元生成的2-群,P2为2元生成的3-群,P3为素数幂阶循环群. (11)当s=2时,若只有d1≥2,由引理3可得 没有满足条件的值使之成立.若d1≥2,d2≥2,由 可知p1=3,d1=2,p2=7,d2=2,故P1是2元生成3-群,P2为2元生成的7-群. 综上当s=2时,G=P1×P2,其中Pi∈Sylpi(G),且P1为2元生成的3-群,P2为2元生成的7-群. 综上当s=1时,G=P1,其中P1∈Sylp1(G),且为2元生成11-群. 利用幂零群理论中的循环子群、Sylow子群的性质给出了恰有12个极大子群的有限幂零群的结构,将极大子群个数对有限群结构的影响扩展到了12个极大子群对有限幂零群结构的影响,为进一步探讨恰有12个极大子群的有限幂零群所具有的其他性质提供了便利.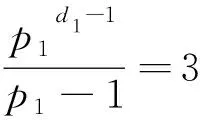
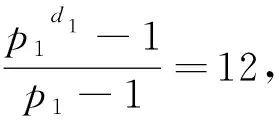
3 结语
