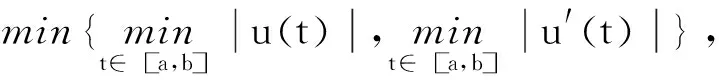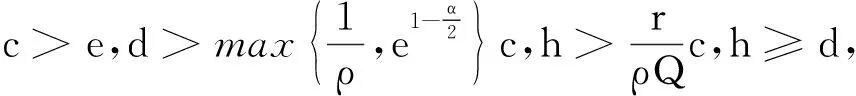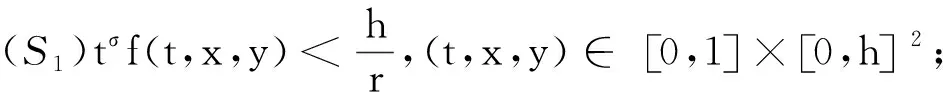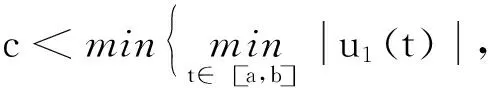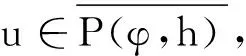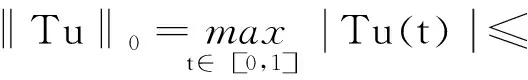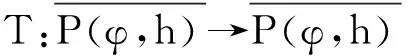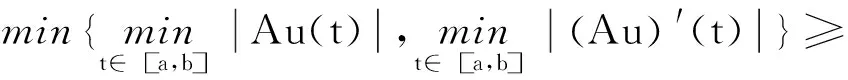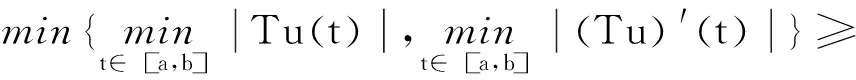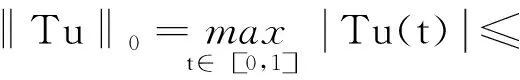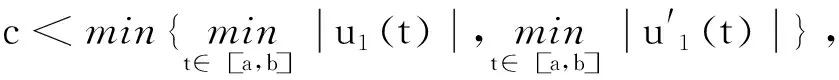一类非线性分数阶微分方程三个正解的存在性
2022-05-02杨旭升
杨旭升,魏 嘉
(兰州文理学院 教育学院,甘肃 兰州 730000)
0 引言
非线性分数阶微分方程边值问题是边值问题的一个重要组成部分.非线性分数阶微分方程是传统的非线性整数阶微分方程的衍生和推广.通过对很多非线性分数阶微分方程问题的探讨,可以知道非线性分数阶微分方程模型要比非线性整数微分方程模型更加实用、更加精确、更具推广性.近年来,非线性分数阶微分方程边值问题在材料力学、生物学、物理学、粘弹性理论、控制工程、多孔介质等研究领域都有广泛应用,与此同时愈来愈多的科研工作者对非线性分数阶微分方程边值问题产生了浓厚兴趣并取得了一些很好的研究成果[1-5].
2012年,Xu[6]研究了分数阶微分方程边值问题
正解的存在性.其中,1<α≤2,2≤β,η≤1.
2015年,Ma[7]研究了分数阶微分方程边值问题
正解的存在性.其中,2<α≤3,m>1是整数,βi>0,1 受此启发,本文研究分数阶微分方程边值问题 (1) 令E=C1[0,1]是一Banach空间且有范数 ‖u‖=max{‖u‖0,‖u′‖0}, 其中 ‖u‖0=maxt∈[0,1]|u(t)|, 为了讨论边值问题(1)正解的存在性,做如下假设: f:(0,1]×R+×R+→R+,并且存在一常数0<σ<1使得tσf(t,x0,x1)在 [0,1]×R+×R+上连续,其中R+=[0,+∞). 另外,假设φ,θ是P上非负的连续凸泛函,φ是P上非负的连续凹泛函,ψ是P上非负的连续泛函,则对于非负数e,c,d,h,定义如下的凸集: P(φ,h)={x∈P/φ(x) 本文所用的工具为Avery-Henderson不动点定理. φ(x)≤ψ(x) 且‖x‖≤Lφ(x), (1){x∈P(φ,θ,φ,c,d,h):φ(x)>c}≠∅, 并且对于x∈P(φ,θ,φ,c,d,h)有φ(Ax)>c; (2)对于x∈P(φ,φ,c,h)有φ(Ax)>c和θ(Ax)>d; (3)0∉R(φ,ψ,e,h),ψ(Ax) 并且 c<φ(x1),e<ψ(x2), φ(x2) 引理1给定y∈L1[0,1]∩C(0,1),则边值问题 (2) 的解可以表示为 其中 证明将式(2)中的方程变为与之等价的积分方程 其中C1,C2,C3∈R,即有 利用式(2)中边界条件,可得 再由u′(1)=γu(η),可得 其中: 即有 引理2存在a,b∈(0,1),且a 其中: 证明由于P′(s)≥0,s∈[0,1],故P(s)关于s是非减的,因此对于任意的s∈[0,1],有 显然 即对于t,s∈[0,1],有 一方面,当0≤s≤t≤1时,有 当0≤t≤s≤1时,有 G(t,s)≥0. 另一方面,当0≤s≤t≤1时,有 对于任意的t∈[a,b],s∈[0,1],有 在C1[0,1]上定义锥P: 为了证明边值问题(2)有一个正解u(t),得证明当且仅当u是T在P上的一个不动点. 引理3算子T:P→C1[0,1]是连续的. (3) 由于‖un-u‖→0,对于上面的δ>0,存在N,使得当n>N,对任意的t∈[0,1],有 |un(t)-u(t)|≤‖un-u‖<δ, 于是,对于任意的t∈[0,1],n>N,由式(3),有 (4) 所以,对于n>N,t∈[0,1],由式(4),有 和 可得 ‖Tun-Tu‖→0,(n→∞), 即T在C1[0,1]是连续的. 引理4T:P→P是全连续的. 证明由定理2可得 (Tu)(j)(t)≥0(j=0,1),t∈[0,1] 和 因此 易证T(P)⊂P.对于任意有界集V 在P上定义凸函数ψ(u)=φ(u)=φ(u)=‖u‖,且定义凸泛函 其中a,b如引理2所述. 取u(t)=cet-0.5a,t∈[0,1],可得u∈P,‖u‖ {u∈P(φ,θ,φ,c,d,h):c<φ(u)}≠∅. 对于u∈P(φ,θ,φ,c,d,h),由(S2)得 其次,取u∈P(φ,φ,c,h),‖Tu‖>d.由Tu∈P,有 最后,由于ψ(0)=0,所以0∈R(φ,ψ,e,h).取u∈R(φ,ψ,e,h),ψ(u)=‖u‖=e,由(S3)得 故ψ(Tu)=‖Tu‖ 综上,定理1的条件全部满足,分数阶微分方程(1)至少存在三个正解u1,u2,u3,且满足
‖u′‖0=maxt∈[0,1]|u′(t)|.
{x∈P/φ(x)≥c,φ(x)≤h};
P(φ,θ,φ,c,d,h)=
{x∈P/c≤φ(x),θ(x)≤d,φ(x)≤h};
R(φ,ψ,e,h)=
{x∈P/e≤ψ(x),φ(x)≤h}.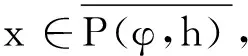
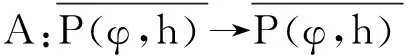
1 预备知识
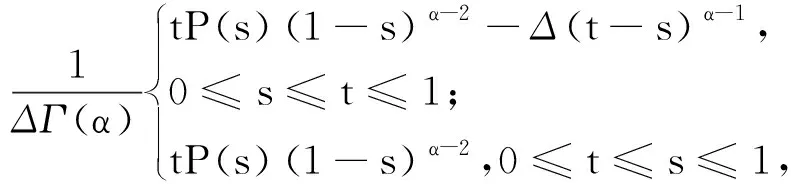

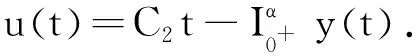

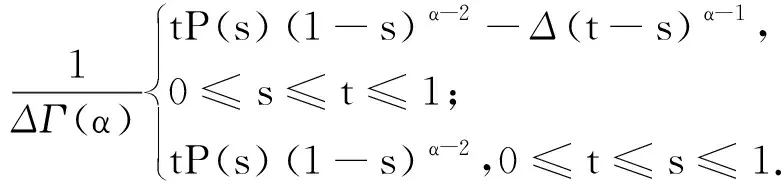
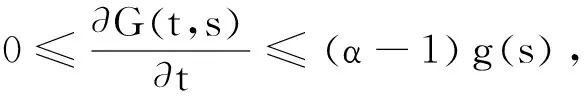
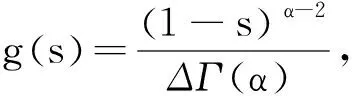
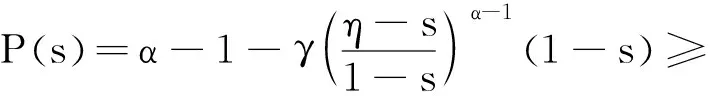
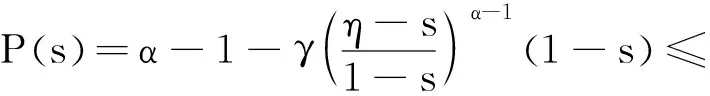
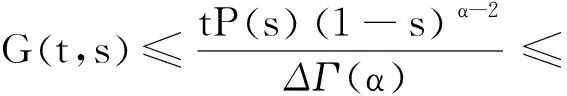
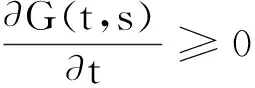
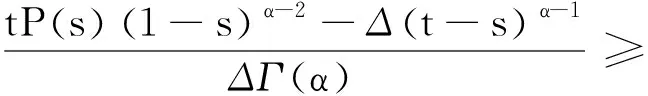
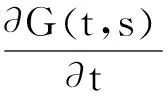
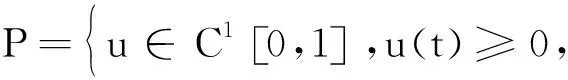
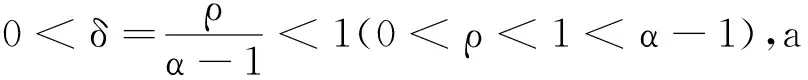
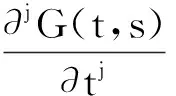
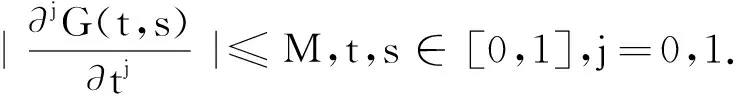
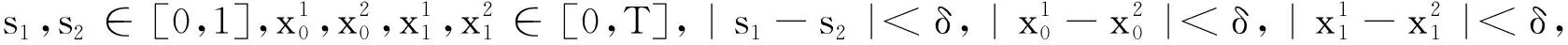
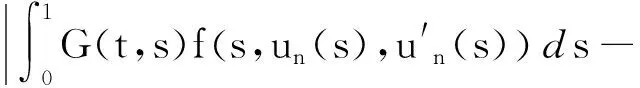
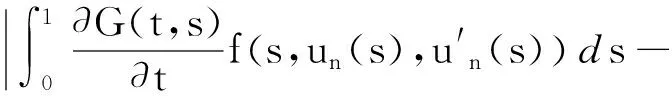
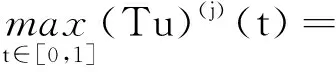
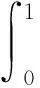
2 主要结果