俯冲带板内地震竖向加速度谱阻尼修正系数模型研究＊

2022-05-02陈心锋姜妍旭刘名吉

地震学报 2022年2期

陈心锋姜妍旭刘名吉

（中国济南 250000 山东建筑大学土木工程学院）

引言

随着震害调查及地震工程认识的深入，多项研究表明实际工程中竖向地震作用对建筑物影响显著，而且竖向地震动反应谱不能简单地根据竖向与水平向反应谱（V/H）的比值得出.Ambraseys和Douglas （2003）以及Bozorgnia和Campbell （2004）通过对V/H反应谱比值的统计分析得出短周期的竖向地震动幅值超过了相应的水平向地震动，这与抗震规范中通常规定的V/H比值为2/3的推荐值存在较大差异.许多现行的抗震规范设计谱和地震动衰减关系的预测反应谱均基于5%阻尼比，但结构的阻尼比并不全为5%，一些长悬臂桁架和大跨度空间桁架的阻尼比小于5%，具有附加阻尼装置结构的阻尼比大于5% （Xiang，Huang，2019）.通常设计高阻尼比结构的目的是减少结构变形和减小结构全加速度以保护结构内置设备，对于质量为m，阻尼系数为c，刚度为k的单自由度结构，在地震加速度时程为作用下的动态平衡方程表示为

式中，为结构相对于地面的加速度，为结构相对地面的速度，x为结构相对于地面的位移，为结构的全加速度.对于一个给定的结构，通过增加阻尼比来减小全加速度意味着减小固定在结构内部所有非结构部分的加速度，全加速度反应谱值则为在给定结构周期下的最大值.

获得不同阻尼比下的反应谱可以通过建立不同阻尼比下的地震动衰减关系来实现，但由于需要的参数过多难以应用于工程设计，因此，建立阻尼修正系数（damping modification factor，缩写为DMF）模型来得到不同阻尼比下的设计反应谱得到了广泛应用.DMF模型为同一周期下任意阻尼比反应谱谱值与5%阻尼比反应谱谱值的比值，其加速度反应谱的阻尼修正系数可表示为

式中，Ba表示加速度反应谱阻尼修正系数，ζ为阻尼比，T为谱周期，S（aT，ζ）和S（aT，5%）分别表示阻尼比为ζ和5%时的全加速度反应谱值.竖向DMF模型与水平向DMF模型差异显著（Rezaeianet al，2014），难以利用某一特定值或函数转化，而且竖向与水平向模型的标准差差别较大，因此需单独建立竖向DMF模型.

Newmark和Hall （1982）根据少量的地震记录首次建立了DMF模型，该模型仅把阻尼比作为参数；Lin和Chang （2003，2004）指出阻尼修正系数对谱周期的依赖性，建立了考虑阻尼比和谱周期的DMF模型；蒋建等（2009）分四类场地研究了场地条件对阻尼修正系数的影响，通过非线性回归方法建立DMF模型，研究表明场地条件对DMF的影响程度随着阻尼比的增大而逐渐增大；郝安民等（2012）建立了考虑矩震级和场地类别的加速度反应谱DMF模型，证实了矩震级和场地类别对DMF的影响是显著的；Li和Chen （2017）采用一个衰减系数来代替矩震级、震中距离和场地条件对阻尼修正系数的影响，建立了加速度谱的DMF模型；Xiang和Huang （2019）利用3 198条竖向地震动记录，证实了阻尼修正系数的概率特性呈正态分布，并研究了矩震级、震中距离、震源深度、场地条件以及峰值加速度对阻尼修正系数的影响.规范设计反应谱中并不包含有关地震特性的参数，因此，建立只考虑场地类别、阻尼比和谱周期的DMF模型是有必要的.

我国强震台网建设起步较晚，而DMF模型的建立对强震记录有一定的质量要求，本文拟基于K-NET和KiK-net台网记录的日本俯冲带地区的板内竖向地震数据，根据场地周期划分场地类别，将地震记录数据分成四类，分别建立不同场地类型下的DMF模型，用于调整地震震源和距离参数未知的设计反应谱来得到非5%阻尼比反应谱，随后采用随机效应模型进行残差分析，以探究震源、路径和场地效应对DMF模型残差及标准差分布的影响.

1 强震数据

根据Zhao等（2015）关于地震动类型的定义，日本俯冲带地震按照震源所处的构造位置、断层机制以及俯冲板块边界几何形状可分为浅壳及上地幔地震、板间地震和板内地震.在震级、震源距离和场地条件均相同的情况下，俯冲带板内地震的短周期反应谱往往高于其它类别的地震.俯冲带地质构造复杂，为了提高地震动衰减模型的拟合度，分地震类别建立地震动衰减关系模型是必须的（Jiang，Zhao，2017），现给出俯冲带板内地震竖向加速度谱的阻尼修正系数模型，俯冲带板内地震定义为：① 震源深度在50 km以内，且位于俯冲板界面深度5 km以下，断层机制为正断层或走滑断层；② 在俯冲板界面深度以下并且震源深度大于50 km.

本文使用的日本强震记录均采用以下方式处理：① 仅使用MW≥4.9的强震记录；② 剔除波形不完整或者波形有明显错误的记录；③ 对地震记录进行采集仪器的校正和基线校正；④ 滤波：对于短周期，采样率为50 Hz和100 Hz的记录，分别选择24.5 Hz和33.3 Hz作为低通滤波器的最大截止频率；对于长周期，由于加速度强震仪在长周期噪声较强，所有地震记录的高通滤波截止频率都需要通过人工确定，大震近场记录的截止频率最小可达0.05 Hz，小震远场记录最高可达2.0 Hz.

为了更好地建立模型，需要将处理获得的数据进行筛选，筛选标准为：① 剔除由于处理过程缺少竖向分量的地震记录；② 为避免未触发台站等影响，采用与震级关联的距离截断方法，最大距离为300 km；③ 地震记录应拥有可达基岩深度的实测剪切波速和可靠的震源位置以及震源机制参数.最终从日本K-NET和KiK-NET强震台网获取了4 695条俯冲带板内竖向地震记录.

根据目前已有的DMF模型（Zhou，Zhao，2020），场地效应是重要的模型参数.本文使用日本公路桥梁设计规范（Japan Road Association，1980）根据表面冲积土和洪积土层厚度以及场地周期提出的场地分类方法.在早期的研究中，日本的绝大多数场地没有任何场地信息.Zhao等（2006a）使用改进的横向和竖向反应谱比值进行了场地分类，利用该场地类别，Zhao等（2006b）建立了一种地震动衰减关系并能够较好地模拟场地共振效应，表明Zhao等（2006a）的近似场地分类方法可行.随着日本K-NET和KiK-net的投入使用，近十余年来，上述两个台网记录到了大量地震且很多台站有了深达基岩的实测剪切波波速.Zhao等（2016a，b，c），Zhao等（2017）以及Jiang和Zhao （2017）根据模型最大似然值判定，排除无场地实测波速的地震记录后能够改善模型精度.因此本文使用Zhao等（2016c）使用的强震数据，并且场地都有实测的剪切波波速.据此，本文根据台站实测的场地剪切波速计算得到场地周期，即

式中，Ts为场地周期，h为基岩上覆土层的深度，vS为h范围内的垂直入射剪切波传播时间加权平均剪切波速.

本文模型通过与Jiang和Zhao （2017）提出的5%阻尼比水平下俯冲板内地震的竖向地震动衰减关系相乘来检验非5%阻尼比反应谱曲线的拟合效果，因此采用与Jiang和Zhao（2017）一致的场地划分.表1给出了每类场地所处的场地周期范围，用 Ⅰ ， Ⅱ ， Ⅲ和Ⅳ表示四类场地，分别表示日本公路桥梁设计规范（1980版）中的场地类别描述（岩石、硬土、中硬土和软土），并给出了各类场地的记录数量.图1给出了地震记录关于矩震级和断层距离（当断层模型可用时，为断层面至台站的最短距离，否则取震源距离）以及矩震级和断层深度（当断层模型可用时，为断层顶部至地面的竖直距离，否则取震源深度）的分布图.

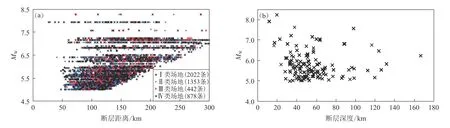
图1 地震数据分布图（a）地震记录关于矩震级和断层距离的分布；（b）地震事件关于矩震级和断层深度的分布Fig. 1 The distribution of earthquake dataset（a） The distribution of earthquake records with respect to moment magnitude and source distance；（b） The distribution of earthquakes with respect to moment magnitude and fault depth

表1 场地类别定义和各类场地记录数量Table 1 Site class definition and number of the records in each site class

本次研究选取4 695条地震记录，按照四种场地类别分别计算1%—4%，6%—10%，15%，20%，25%和30%阻尼比下36个谱周期点（0.01—5.0 s）的加速度谱的DMF几何均值.

图2给出了1%，3%，15%和30%阻尼比下阻尼修正系数几何均值随谱周期变化的关系曲线.可以看出：① 谱周期小于0.03 s时，阻尼修正系数均值在不同阻尼比和不同场地类型下都近似为1.0，这是由于周期过短，结构地震反应与地面震动相似所致；② 阻尼修正系数在谱周期0.03—0.16 s时逐渐增大，在谱周期大于0.16 s时逐渐减小；③ 阻尼较大时，阻尼修正系数变化趋势呈现与小阻尼相反的变化趋势.值得注意的是，在长周期，随着谱周期的增大阻尼修正系数增加至1.0以上，反映了阻尼力对绝对全加速度谱的影响，在高阻尼比长周期的情况下，由于忽略阻尼力，导致抗震设计偏于保守；④ 在谱周期0.03—0.1 s时，Ⅰ类场地的阻尼修正系数与其余场地类型差异明显；在谱周期较长时，Ⅳ类场地的阻尼修正系数与其余场地类型差异明显，说明谱周期接近场地周期时的阻尼修正系数变化较大.

图2 四类场地阻尼修正系数DMF的几何均值分布情况Fig. 2 The geometric mean values of DMF for four site classes（a） ζ＝1%；（b） ζ＝3%；（c） ζ＝15% ；（d） ζ＝30%

不同场地的阻尼修正系数差异较大，针对场地条件对阻尼修正系数的影响，根据Zhao等（2019）建立一个考虑谱周期与场地周期的场地效应影响模型，即

式中，b（T，ζ）和c（T，ζ）是与场地周期无关的模型参数，T为谱周期，Ts为场地周期.

给定场地周期下的阻尼修正系数可以根据式（6）计算得出，即

式中m为模型回归系数.根据式（3），可以推导出场地效应对Ba的影响，即

式中Ts1和Ts2为两类不同场地的场地周期.

由式（7）可以得出DMF比值与场地周期比值在对数刻度下呈线性关系，根据Zhao等（2019）的研究，m值在高阻尼短周期下为正值，由此可以解释图2c和2d中 Ⅰ 类场地在短周期下DMF值较小的情况；m值在高阻尼长周期下为负值，可以解释图2c和2d中Ⅳ类场地在中长周期下DMF值较小的情况.

为了验证分场地类别建立模型的必要性，采用统计量Z检验不同场地下阻尼比为1%，3%，15%和30%时阻尼修正系数的差异性，当统计量Z处于拒绝域内时，所检验的不同场地下的阻尼修正系数差异显著.统计量Z的计算公式为

式中，Z为检验统计量，和分别为同周期不同场地类别的阻尼修正系数样本均值，和表示同周期不同场地类别的阻尼修正系数样本方差，nX和nY表示两类场地各自的阻尼修正系数样本容量，置信水平取为5%，拒绝域|Z|≥1.96.

图3给出了阻尼比分别为1%，3%，15%和30%时四类场地差异性检验统计值|Z|的分布图.由于不同场地类别在谱周期为0.01 s时的Ba相近，图3未给出谱周期为0.01 s时的|Z|值.由图3a-3c中Ⅰ 类场地与其余场地的对比可以看出：谱周期在Ⅰ 类场地的场地周期附近时，|Z|值达到最大；在长周期|Z|值较小，尤其是Ⅰ 类场地与Ⅱ类场地的对比，谱周期大于0.32 s时，|Z|值基本小于1.96；在谱周期大于0.04 s时，阻尼比为1%的|Z|值一般大于30%阻尼比下的|Z|值，其原因是阻尼比为30%下不同场地类型的DMF均值差异小于1%阻尼比下不同场地类型的DMF均值；同一谱周期下，Ⅰ 类场地与Ⅳ类场地的|Z|值基本大于Ⅰ 类场地与 Ⅱ 类场地的|Z|值及Ⅰ 类场地与Ⅲ类场地的|Z|值，Ⅱ类场地与Ⅳ类场地的|Z|值基本大于 Ⅱ 类场地与Ⅲ类场地的|Z|值，这种情况可以用式（7）来解释，场地周期差异较大时，阻尼修正系数差异也就越大.从这些结果可以看出，在多数周期上，四种场地类别下DMF均值统计显著不同，因此有必要分场地类别来建立DMF模型.

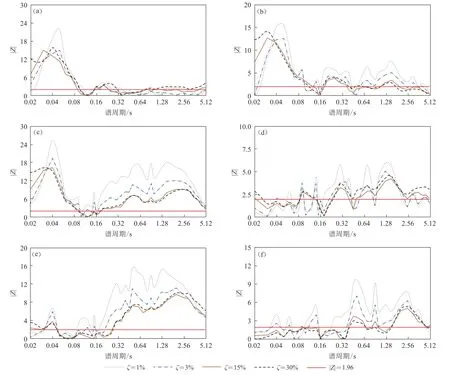
图3 四类场地间显著性检验统计值|Z|（a） Ⅰ类场地与Ⅱ类场地；（b） Ⅰ类场地与Ⅲ类场地；（c） Ⅰ类场地与Ⅳ类场地；（d） Ⅱ类场地与Ⅲ类场地；（e） Ⅱ类场地与Ⅳ类场地；（f） Ⅲ类场地与Ⅳ类场地Fig. 3 |Z| values for the statistical tests between each pair of four site classes（a） Site class Ⅰ vs site class Ⅱ；（b） Site class Ⅰ vs site class Ⅲ；（c） Site class Ⅰ vs site class Ⅳ；（d） Site class Ⅱ vs site class Ⅲ；（e） Site class Ⅱ vs site class Ⅳ；（f） Site class Ⅲ vs site class Ⅳ

2 加速度谱阻尼修正系数模型的建立

分四种场地类别对阻尼修正系数几何均值进行回归分析，并结合俯冲带板内地震特性，考虑阻尼比和谱周期对阻尼修正系数的影响，给出俯冲带板内地震竖向加速度谱阻尼修正系数模型的表达式为

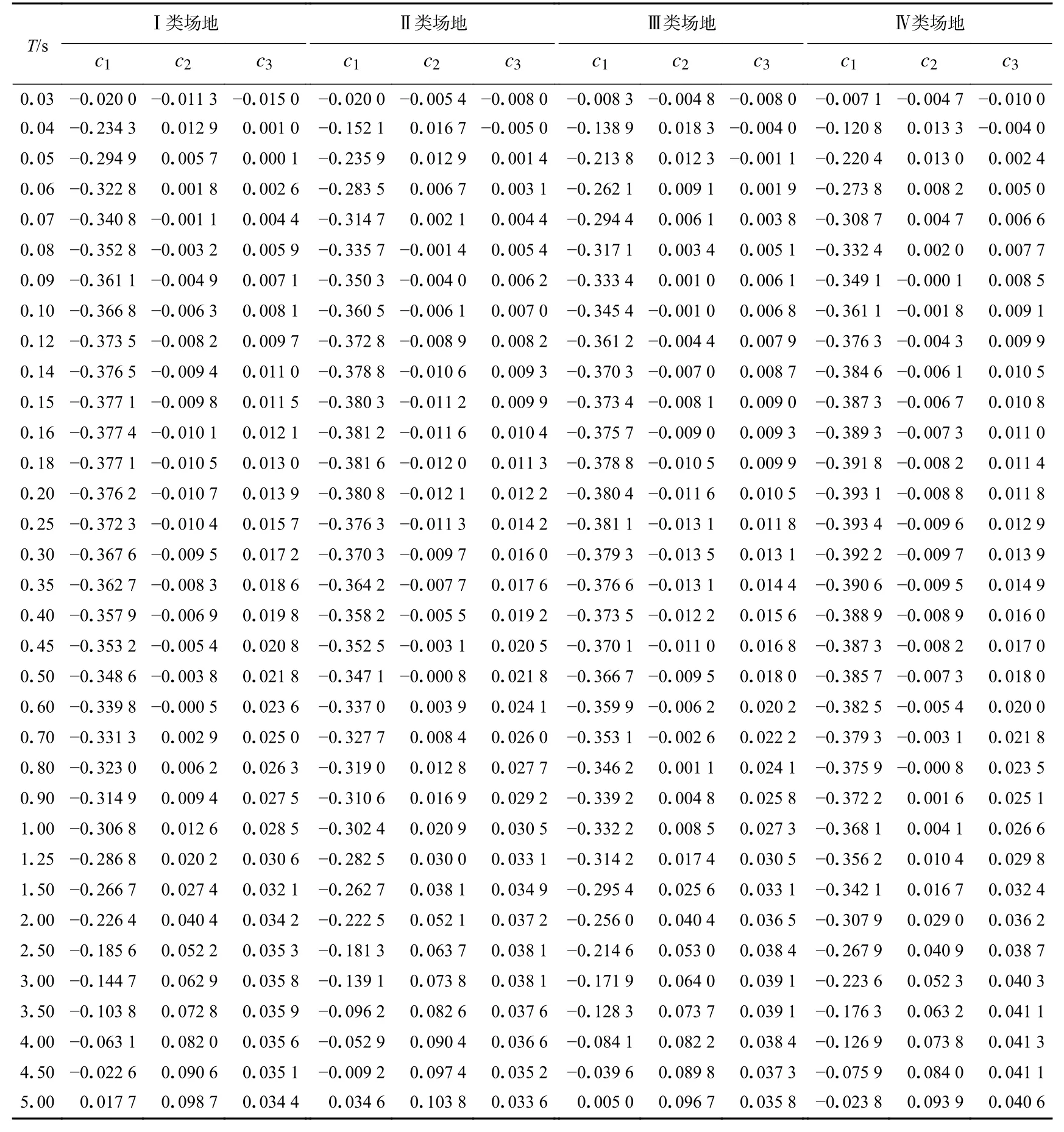
表2 四类场地下阻尼修正系数模型的系数值Table 2 Coefficients of DMF model for four site classes

图4给出了 Ⅰ —Ⅳ类场地阻尼修正系数模型曲线与原始数据几何均值散点的对比.由图4a和4b可见：较高阻尼比的模型值与数据值在谱周期0.03 s时存在偏差，原因是为了得到更加平滑的反应谱曲线，适当调整了较高阻尼的模型系数，在其它阻尼比谱周期下，模型曲线与数据值都有着良好的拟合效果；高阻尼比的DMF模型在长周期时超过1.0，这可以用来解释长周期结构附加过大的阻尼比，虽可以降低结构的位移反应，但并不能有效地降低地震作用，甚至会增大地震作用对长周期结构的影响.

图4 四类场地不同阻尼比的阻尼修正系数DMF模型拟合曲线与数据几何均值的对比（a） Ⅰ类场地；（b） Ⅱ类场地；（c） Ⅲ类场地；（d） Ⅳ类场地Fig. 4 DMF model comparisons with the geometrical mean of the vertical components for eight damping ratios of four site classes（a） Site class Ⅰ；（b） Site class Ⅱ；（c） Site class Ⅲ；（d） Site class Ⅳ

3 残差分析

为了进一步评估模型的拟合效果，对模型进行残差分析，残差定义为

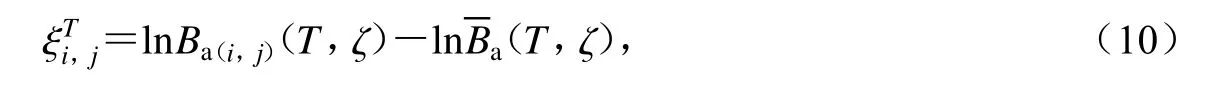
为探究震源、路径和场地效应对模型产生的误差影响，根据Brillinger和Preisler （1984）采用随机效应模型对地震动衰减关系进行回归分析的方法，结合Abrahamson和Youngs （1992）提出的改进的随机效应模型，将总残差分离为事件内残差和事件间残差，即

式中：ηi表示均值为0，标准差为τ的事件间残差；ξi，j表示均值为0，标准差为σ的事件内残差，其中总标准差.

为进一步分析路径效应、场地效应对残差分布的影响，将事件内残差分解为场地间残差和场地内残差，即

表3 阻尼修正系数模型的总残差标准差σTTable 3 Total standard deviations σT of DMF model

图5a-d分别给出了总残差标准差、事件间标准差和事件内标准差关于谱周期变化的分布图，由该图可见：在谱周期0.01—0.03 s内，事件内标准差和事件间标准差数值较小且相差不显著；在大多数谱周期下低阻尼的事件内标准差大于事件间标准差（图5a，b），表明同一地震记录存在的离散性较大，由此认为震源效应引起的误差在低阻尼的大多数谱周期情况下小于其它因素；在高阻尼长周期的情况下，事件内标准差小于事件间标准差（图5c，d），可以认为震源效应在高阻尼长周期引起的误差大于其它因素.

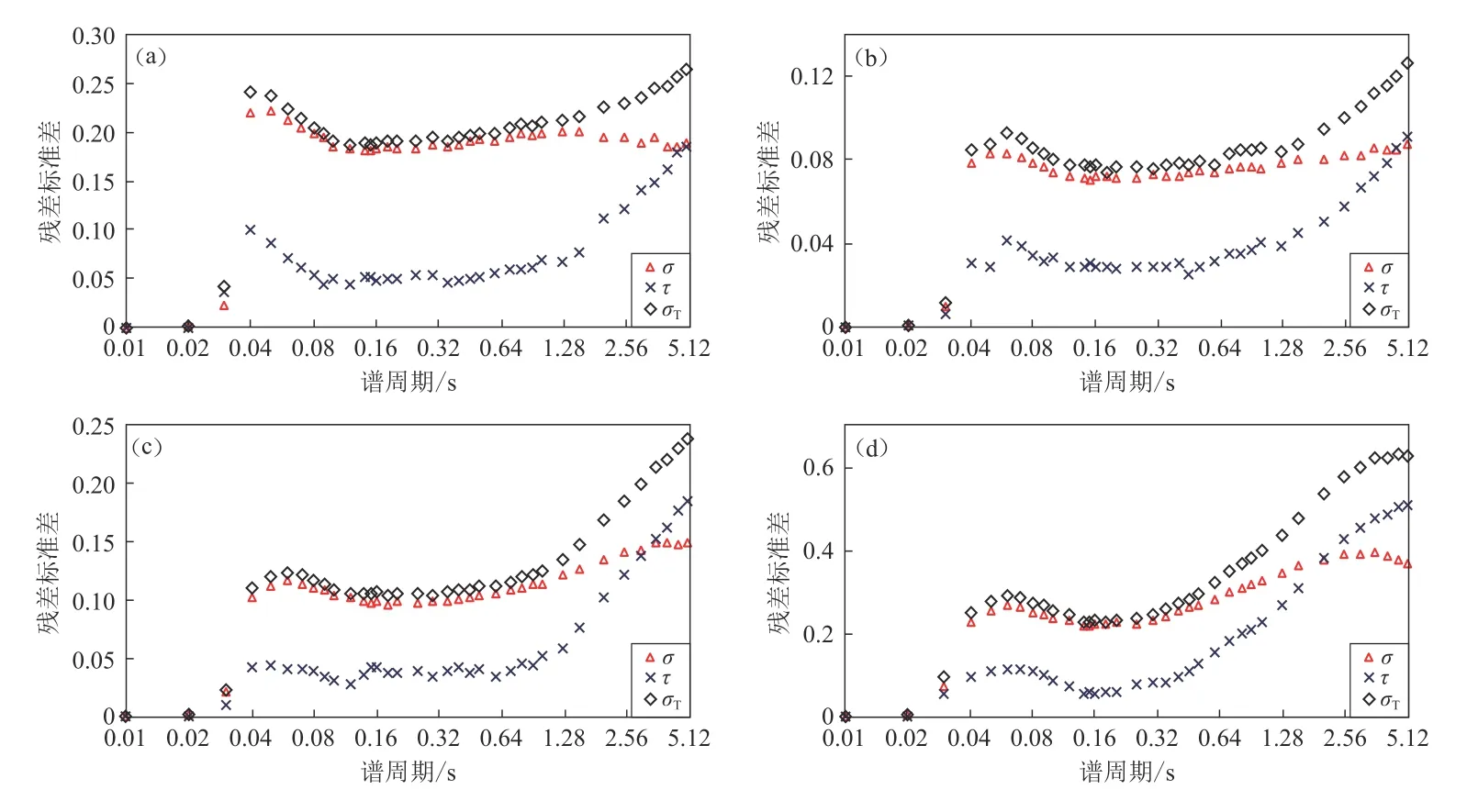
图5 阻尼修正系数DMF模型的残差标准差关于谱周期的分布图Fig. 5 The distribution of standard deviations of DMF models（a） ζ＝1%；（b） ζ＝3%；（c） ζ＝10%；（d） ζ＝30%

图6给出了阻尼比为25%情况下的场地内标准差和场地间标准差随谱周期的分布图.由图6可知：在谱周期小于0.06 s时， Ⅰ 类场地的场地内标准差和场地间标准差均大于其余场地，表明 Ⅰ 类场地在短周期的离散性较大，受路径和场地效应影响较大；在谱周期小于0.10 s时，场地内标准差小于场地间标准差，表明短周期范围内场地效应引起的误差大于路径效应引起的误差；在谱周期大于0.10 s时，场地内残差大于场地间残差，表明中长周期范围内场地效应引起的误差小于路径效应引起的误差.理论上场地内残差主要来自于路径效应，导致场地内标准差与场地类别基本无关，而各类场地的场地间标准差则与场地类别在中长周期有一定的关系.

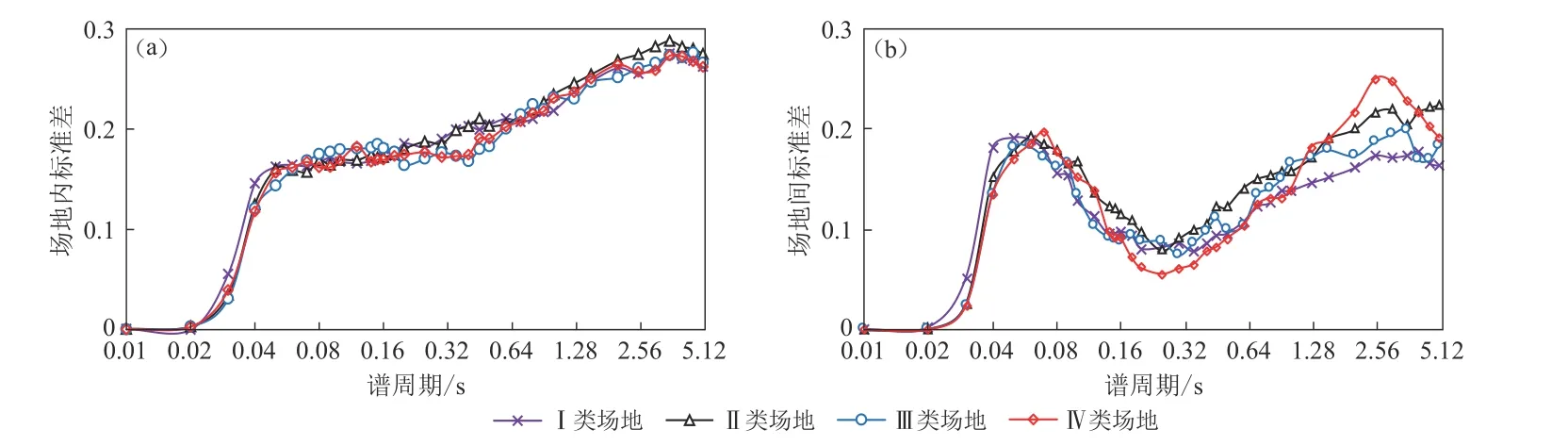
图6 阻尼比为25%时四类场地的场地内标准差（a）和场地间标准差（b）分布图Fig. 6 Distribution of within-site （a） and between-site （b） standard deviation for four site classes for a damping ratio of 25%

表4 阻尼修正系数模型的事件内残差标准差σTable 4 Within-event standard deviation σ of DMF model

为了更加直观地分析模型残差，采用最小二乘法对标准差进行拟合，拟合公式为

表5 阻尼修正系数模型的事件间残差标准差τTable 5 Between-event standard deviation τ of DMF model

式中，α，μ，λ为模型回归系数，k为场地类别.

图7给出了四类场地DMF模型标准差关于对数坐标系下的阻尼比变化图，由该图可见，以阻尼比5%为界，标准差随阻尼比的变化呈现不同的趋势.然而在推导模型系数时，式（13）并不满足DMF模型的边界条件，即不满足在阻尼比等于5%时，标准差等于零，这是因为在阻尼比接近5%时，标准差很小，不会影响残差模型的准确性，而如果强制满足边界条件，会使得标准差显著增大.

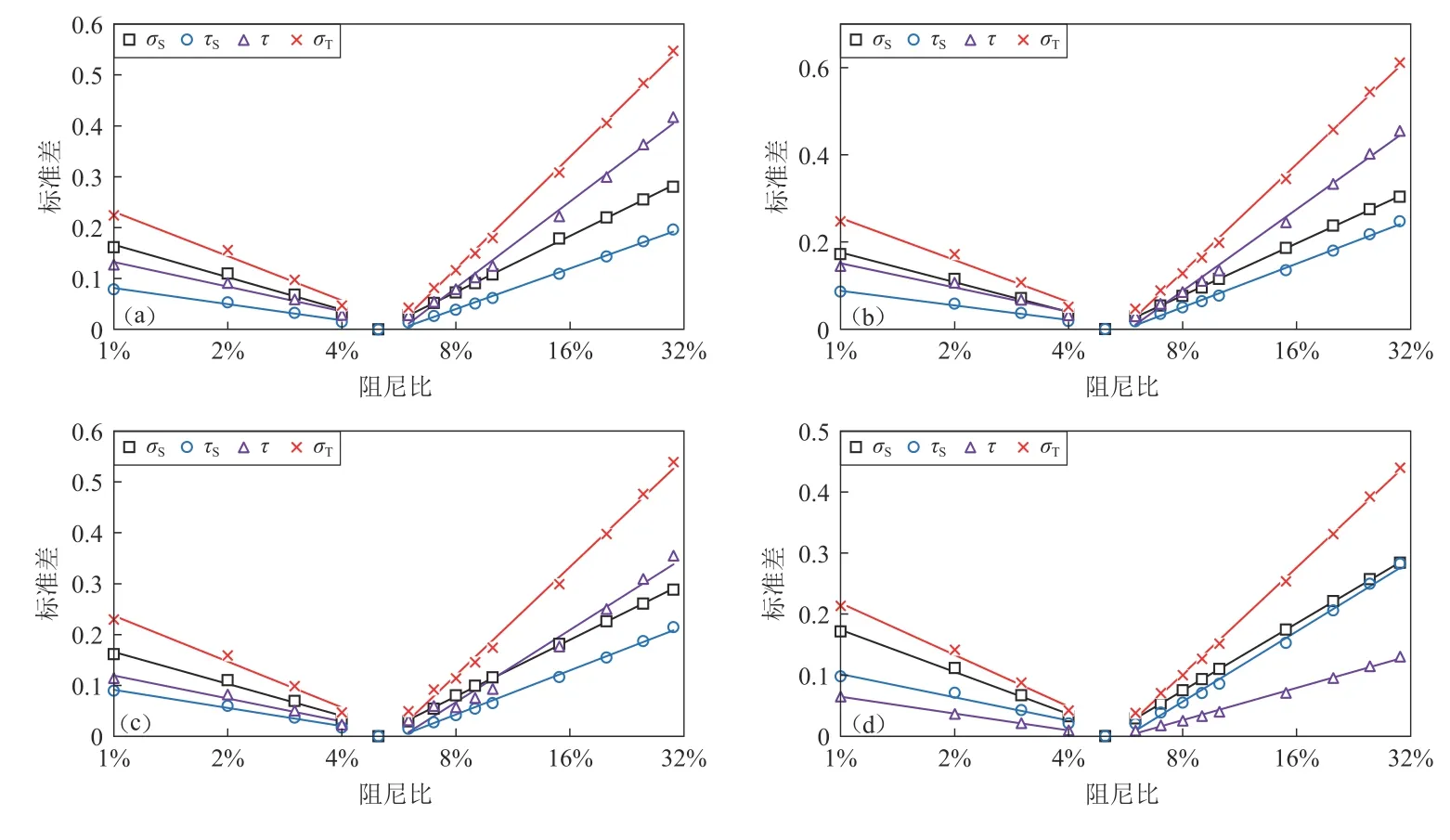
图7 T＝2.5 s时阻尼修正系数DMF模型标准差关于对数坐标系下阻尼比的变化图（a） Ⅰ类场地；（b） Ⅱ类场地；（c） Ⅲ类场地；（d） Ⅳ类场地Fig. 7 Variations of standard deviation of DMF model with damping ratio at logarithmic scale by T＝2.5 s（a） Site class Ⅰ；（b） Site class Ⅱ；（c） Site class Ⅲ；（d） Site class Ⅳ

图8给出了阻尼比为25%，谱周期分别为0.10 s和3.0 s时的事件间残差关于矩震级和断层深度的分布图.由图可见，残差图的趋势线斜率不为零，矩震级和断层深度对事件间残差分布有一定影响，表明未考虑矩震级和断层深度的模型拟合度欠佳.由图8a和8c可见，短周期与长周期下的事件间残差拟合线斜率正负不一致，表明模型可能在不同周期对矩震级的评估不一致.由图8b和8d可见，短周期与长周期下的事件间残差拟合线斜率正负不一致，表明模型可能在不同周期对断层深度的评估不一致，存在低估或高估的情况.

图8 阻尼比为25%时阻尼修正系数DMF模型事件间残差分布图（a） T＝0.1 s时残差关于断层深度的分布图；（b） T＝0.1 s时残差关于矩震级的分布图；（c） T＝3.0 s时残差关于断层深度的分布图；（d） T＝3.0 s时残差关于矩震级的分布图Fig. 8 The distributions of between-event residuals of DMF model for a damping ratio of 25%（a） The distribution of residuals with respect to fault depth at T＝0.1 s；（b） The distribution of residuals with respect to moment magnitude at T＝0.1 s；（c） The distribution of residuals with respect to fault depth at T＝3.0 s；（d） The distribution of residuals with respect to moment magnitude at T＝3.0 s

图9给出了阻尼比为25%，谱周期分别为0.10 s和3.0 s时的事件内残差关于断层距离和矩震级分布图.由图9a和9b可见，趋势线几乎水平，表明矩震级对事件内残差分布的影响很小.由图9c和9d可见，短周期与长周期下的事件内残差拟合线斜率正负不一致，表明模型在不同周期可能对断层距离的评估不一致，存在低估或高估的情况.综上可见，本文提出的DMF模型可用于调整不考虑地震震源和距离参数的设计反应谱，模型残差分布与地震动参数存在相关性，其中矩震级和断层深度对事件间残差分布有影响，事件内残差分布与断层距离显著相关，因此对于地震震源和距离参数可知的设计反应谱，DMF模型应考虑矩震级、断层距离和断层深度等因素的影响.

图9 阻尼比为25%时DMF模型事件内残差分布图（a） T＝0.1 s时残差关于断层距离的分布图；（b） T＝0.1 s时残差关于矩震级的分布图；（c） T＝3.0 s时残差关于断层距离的分布图；（d） T＝3.0 s时残差关于矩震级的分布图Fig. 9 The distributions of within-event residuals of DMF model for a damping ratio of 25%（a） The distribution of residuals with respect to fault distance at T＝0.1 s；（b） The distribution of residuals with respect t moment magnitude at T＝0.1 s；（c） The distribution of residuals with respect to fault distance at T＝3.0 s；（d） The distribution of residuals with respect to moment magnitude at T＝3.0 so