一种FBMC 系统干扰分类预处理方案①

赵清华 马天鸣 王 星

(上海工程技术大学电子电气工程学院 上海 201620）

0 引言

基于偏移正交幅度调制(offset quadrature amplitude modulation,OQAM)的滤波器组多载波(filter bank multicarrier,FBMC)[1]是一种非正交的多载波传输技术,该技术利用时频聚焦特性优良的原型滤波器[2-3]代替正交频分复用(orthogonal frequency division multiplexing,OFDM)中的矩形窗函数来降低带外发射功率,而且能在不需要任何循环前缀的前提下对多径衰落信道有很好的鲁棒性,因此FBMC被认为是新一代移动通信中能够取代正交频分复用的一种优秀候选方案[4-5]。

然而,与OFDM 不同,FBMC 的优良特性是以牺牲复数正交性为前提的,FBMC 只满足实数域的正交,这使得接收端的数据会包含系统本身产生的干扰影响,因此传统的信道估计方案也不能直接应用在FBMC 上[6]。针对这个问题,目前主要的解决方案分为干扰利用和干扰消除两种。

干扰利用法基于伪导频思想[7],通过对FBMC系统干扰分布的特性分析,导频与导频直接相邻的位置采用三列块状导频的方案来进行信道估计,除中间一列为有效导频位,其他两列置零。文献[8]通过在中间导频序列位置加入虚数来提高伪导频功率,进而得到更精确的信道估计值。文献[9,10]在文献[8]的基础上进一步提高了伪导频功率。文献[11,12]通过三列导频项全部填入已知的虚实项来提高中间一列的伪导频功率,该方案虽然大幅增加了伪导频功率,提高了信道估计的精确值,但引入的虚部数据会对未知数据造成新的干扰,在一定程度上增大了系统误码率。文献[13,14]作了进一步优化,使得系统误码率进一步降低。文献[15]通过子块划分进行整体优化来提升伪导频功率,但干扰利用的方案都是基于三列导频,一方面,在实际运用时很难对其他非直接相邻位造成的未知干扰作进一步处理,另一方面,块状导频的使用极大地浪费了频谱资源。

文献[16]根据FBMC 干扰特性提出了基于辅助项消除直接邻位干扰的方案,该方案计算复杂度低,并且导频以离散的方式排列,极大地节省了频谱资源,但这种方法存在辅助项功率过高的问题。文献[17,18]利用FBMC 系统原型滤波器的干扰对称性提出了两种基于干扰消除的块状导频序列方案,这两种方案通过对已知导频序列的合理排列达到了干扰对称消除的目的,在实际应用中可以实现消除直接邻域干扰的效果。但是该类方案的问题在于块状干扰消除导频的使用既无法像干扰利用方案那样可以进一步提高信道估计性能,达到降低系统误码率的效果,也无法做到类似离散导频方案的高效频谱资源利用以及实现系统干扰的完全消除。文献[19]重新回到离散导频的消除干扰方案,给出了辅助导频法(auxiliary pilot,AP)的明确定义并指出了辅助导频法的不足之处,接着提出了一种基于编码法(coding method,Cod)的干扰消除方案。虽然方案在理论上也能达到干扰的完全消除,但这是以增加系统复杂度为代价的,因此在实际应用中也无法做到干扰的彻底消除。文献[20,21]利用迭代法消除的方式进一步优化系统性能,但实际操作时对于迭代值的存取空间处理及本身由于迭代产生的附加时延无法忽略。文献[22]讨论了双选信道下的离散导频方案性能。文献[23]提出的双辅助导频法(double auxiliary pilot,DAP)在传统辅助导频法的基础上通过增加辅助项位数来获得系统性能的改善。文献[24]通过结合编码法和辅助导频法,利用二者在优缺点上的互补特性提出了编码辅助导频法(coding auxiliary pilot,CAP)获得进一步的优化效果。文献[25]提出了一种编码法的简化方案,降低了编码的复杂度,但该方案是以使用辅助导频消除多余干扰为基础的,因此本质上也属于CAP 方案。相对于改进之前的方案,上述改进算法都会增加额外的消耗。

本文提出了一种对发送端导频周围符号进行预处理的方案,将FBMC 中心导频所受周围未知干扰的问题转换为对极少数几个大影响因子数据的处理,从而降低接收端信道估计中对未知干扰处理时的复杂度。经过该预处理方案之后的符号在采用辅助导频方案时可以使得辅助导频功率在不损耗额外频谱资源的前提下获得与平均符号功率一致的结果,在采用编码方案时能够使得算法计算复杂度只与处理后的几个大影响因子符号有关,大幅降低了算法的计算复杂度。

本文各部分内容安排如下:第1 节介绍了FBMC 系统模型。第2 节给出了FBMC 系统2 种传统的离散导频估计方案原理,并且分别指出了它们在实际应用中存在的问题。第3 节提出了一种干扰分类预处理方案,并对两种传统导频估计方案在采用该预处理方案之后的改善情况进行了理论分析。第4 节对所提方案进行了仿真分析。第5 节对全文进行了总结。

1 FBMC 系统模型

假设FBMC 系统的载波数目为N,符号数为M,它的基带等效发送信号可以表示为[18]

其中,am,n是位于时频网格点(m,n)处的数据,gm,n(t)为时频网格点(m,n)处的基函数,g(t)是原型滤波器,v0为子载波之间的间隔,τ0是FBMC 符号之间的时间间隔,φm,n是相位因子。不考虑通道影响,理论上位于(m0,n0)处FBMC 接收信号的表达式为[12]

式(4)为x(t)的自模糊函数,通常用来描述函数x(t)在时频偏移后与自身的相关性[26]。

2 基于导频的信道估计方案

2.1 传统方案

将信道信息加入到式(2)并采用最小二乘法可以得出系统接收端位于时频点(m0,n0)处的信道估计值:

其中,h(t)是信道函数,Hm0,n0是信道在(m0,n0)处的频率响应,wm0,n0是信道噪声,Im0,n0为FBMC 多出来的干扰项。从式(5)可以看出,若直接采用传统方法,即使信道中没有噪声也不能准确地估计出信道的真实值。

2.2 AP 法和预编码方案

2.2.1 AP 法原理

若将(m,n)周围数据对中心位置的干扰系数用um,n=jp+q+p(q+2n0)Ag(-pτ0,-qv0)表示,并且令αn,m=un,m,其中un,m=-um,n,则am0,n0在分析滤波器(analytic filter bank,AFB)输出端所对应的值可以写为

其中,p、q分别代表当前时频格点与中心数据dm0,n0的距离,am0,n0、Im0,n0分别表示经分析滤波器组后,位于(m0,n0)点的数据真实值和周围数据对中心导频数据的叠加干扰项,Ωm,n可以表示为

令Im0,n0=0,即可得到辅助导频位置的幅值表达式为

当增加一个辅助项位数时,该方案就成了双辅助导频法(DAP),此时每个导频对应的额外损耗是2 个有效数据位。

2.2.2 编码法原理

编码法的主要原理是利用正交编码对导频周围所有未知干扰数据进行编码,为了更清晰地解释,这里只对导频的直接邻位进行编码,编码数目为8。

采用类似扩频的方法将导频直接邻位数据的随机数据矩阵An=[a1,a2,a3,…,an]T(n∈N+),扩展到所有一阶邻域内生成新的数据Dn=[d1,d2,d3,…,dn](n∈N+),每个符号下标编号分别对应一个时频点坐标。ak和dm分别为编码前后的数据,m和k分别为编码前和编码后数据下标,若ck表示由ak对扩展后的每个数据的影响系数,那么ak(k=1,2,…,8)对应Dk一组扩展码表示为ck=[c1,k,c2,k,c3,k,…,c8,k]T,同理可以得到扩展后的数据dm(m=1,2,…,8)对应Am的一组编码系数=[cm,1,cm,2,cm,3,…,cm,8]T,据此ak和dm分别可以表示为

上式表明只需Umck=0,无论ak取何值都有I=0,但是[c1,c2,…,c8,U8]是一个维度为8 ×9 的矩阵,必定线性相关,因此编码法也会额外损耗一个有效数据位。所以结合了Cod 法和AP 法的改进CAP 方案也会额外损耗2 个有效数据位。

3 FBMC 信道估计预处理方案

3.1 预处理方案原理及前提条件

通过辅助导频法原理可知,利用额外辅助项的自身干扰可以实现对导频的干扰消除,但即使FBMC 最大的干扰系数项的干扰系数也比1 小,这使得辅助项的功率不能全部用于消除辅助项。这一方面造成了功率额外损耗,另一方面也会对包括自身和其周围符号在内的功率提升,增大了系统的峰值平均功率比。本文将所需干扰消除功率直接加在导频上可以很好地解决以上问题。但产生的新问题是,新引入的消除项为虚数,这使得导频周围未知数据误码率提升。针对这个问题,本文对导频周围符号进行预处理。

设导频周围符号数据为an,其中n∈N,结合式(8)可以得出AP 位置用于干扰消除的叠加项为

由于FBMC 良好的时频聚焦特性,本文所提预处理方案只会对一阶邻域造成有效干扰,因此式(14)矩阵维度为8 即可满足误码率要求,并且求逆矩阵只和原型滤波器系数有关,因此矩阵只需计算一次即可。

由式(14)～(16)可以得出导频周围需要预处理的数据:

其中,N表示位置数据对中心导频有效干扰的最大数目,k1和k2分别代表未被预处理数据的起始和结束的范围。由式(17)可知,处理后的数据值受右式逆矩阵的影响,而逆矩阵的值和干扰矩阵中大干扰系数有直接关系。因此,为保证逆矩阵元素值在可接受范围内,就必须去除其中的大干扰系数影响。当采用PHYDYAS[27-28]原型滤波器时,从表1 中矩阵系数可以直观反映出大干扰系数项的影响。

表1 PHYDYAS 滤波器下包含大系数项的D 矩阵(左8 列)及其逆矩阵(右8 列)

由表2 可以看出,剔除大干扰系数的干扰系数矩阵几乎不会对处理后的符号产生影响。因此本文方法可以将N个位置干扰的处理转换为几个大干扰系数的简单处理。而剔除大干扰系数项也是本文方案的前提条件。下面进一步介绍本方案与其他方法结合的优势。

表2 PHYDYAS 滤波器下不包含大系数项的D 矩阵(左6 列)及其逆矩阵(右6 列)

3.2 预处理方案与辅助导频法的结合

根据预处理方案前提条件,当采用PHYDAYS滤波器时,若导频中心点坐标为(m0,n0),则大干扰项位于(m0+1,n0) 和(m0-1,n0) 处,对不包括(m0+1,n0)和(m0-1,n0)两点在内的其余6 个直接邻位采用预处理,其中(m0+1,n0)保留为辅助项。(m0+1,n0)和(m0-1,n0)在式(15)中分别对应编号7 和8。那么结合式(19)、(20)可以得出:

剩下干扰系数较大的两位可以简单地进行操作来消除干扰,根据FBMC 滤波器对称性,直接令辅助项等于另一个位置数据即可,即令a7=a8,可以看出,此时的辅助位不存在任何功率问题。另外叠加在导频的虚部也会对这两位进行干扰,但是由于这两项的干扰是通过辅助导频法进行额外处理的,叠加项I0和这两个数据的改变无关,因此直接预减去实值干扰即可,即a7=a7-α7I0,a8=a7。虽然I0只和低功率符号干扰有关,并且α7再次降低了干扰影响,但a7与a8幅值还是会受到FBMC 原型滤波器系数的较大限制。比如当采用Hermite 滤波器[17]时,大系数干扰数目为4 个,那么显然与辅助导频方案结合对于辅助项自身缺点的改善不明显。这里再给出另一种思路辅助导频符号取法,可以将这两位的处理看成是特殊的预编码。即令,则在接收端有,这样处理后可以直接消除添加在中心导频的虚部对a7的影响。

3.3 预处理方案与预编码方案结合

本节以具有4 位大干扰系数的Hermite 原型滤波器为例,给出更为通用也更加稳定的干扰消除方案。首先结合式(19)、(20)给出4 位直接相邻的非大干扰系数数据处理方案:

对于大干扰系数项因为只有4 位,直接采用2.2.1节所提编码方案即可。由于编码法需要额外损耗一个有效数据位,结合式(10),其中C4是一个3 行4 列的编码矩阵。可以看出,编码方案受到最大编码位数的限制,但是不受数据幅值改变限制,因此在低数目干扰消除的编码上依然具有很大的优势,对于本方案只需要对4 位进行编解码操作即可。

下面给出无需对编码方案数据中包含I0产生干扰处理的证明,设接收端受到I0干扰后的实值数据为rk=dk+αkI0,Rk=[r1,r2,…,rk],结合式(10)、(11)对Rk进行解码操作:

因此所提预处理方案与编码方案具有很好的兼容性,并且只需对k=5,6,7,8 这4 个大干扰系数位置数据进行编解码操作即可。

3.4 与其他算法结合伪代码示例

由于导频周围固定位置的干扰系数值固定,为简化伪代码,直接令导频周围由大到小排序后的干扰系数和所对应的未处理数据集合分别为U和D,对应邻域内的所有干扰数据位数为N,需要处理的数据位数为N2,其中包含大干扰系数数目为N1,中心导频值用P表示。具体步骤如下。

步骤1对有效干扰数据位N1～N2 进行预处理,得到处理后数据和算法的导频值。

步骤2剩余少数大干扰系数对应的数据采用传统算法,设传统算法为预编码且函数已知。

步骤3将处理好中心导频及周围的数据赋给发送端对应位置。

3.5 计算复杂度分析

由于预处理方案与编码方案具有更好的兼容性,因此下面针对结合编码法的情况进行复杂度分析。

设需要消除干扰位数为N,忽略加法复杂度,若原型滤波器为Hermite 滤波器,首先I0的求取消耗乘法N-4 次,其次4 个直接邻居位小干扰符号共损耗16 次乘法,而其余4 位编解码则损耗了2 ×4×3=24 次乘法,总共损耗复杂度为N+36。而传统编码方案则损耗2N(N-1)次乘法。若N=16,那么对符号预处理和不进行预处理分别损耗复杂度为52 和480,事实上即使对所有符号进行处理,本方案因为无需解码操作,复杂度也仅为编码方案的一半。

4 仿真结果与分析

本节主要对OQAM/FBMC 系统中包括编码法、辅助导频法、双辅助导频法、编码辅助导频法以及本文方案的预处理编码在COST207[29]和VehicularA[30]信道下进行仿真对比分析。其中Prcod 表示采用了本文所提预处理方法与4 编码法结合的方案,Cod4、Cod12、Cod16 则是为了更直观地显示编码法计算复杂度与其精度的关系而分别采用编码数据位数为4、12、16 的编码方案。表3 为仿真参数设置。

表3 仿真参数

首先,对两种信道下的归一化均方误差(normalized mean square error,NMSE)[31]进行仿真,仿真结果如图1 和图2 所示。归一化均方误差的计算表达式如下:

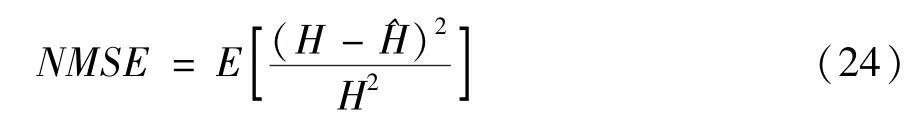
其中E[·]代表求取数学期望。

结合式(5)可知,理论上所有基于干扰消除的方案在消除干扰后,信道具有几乎一致的NMSE 特性,这一点从图1 和图2 可以得出。对于COST207和Vehicular 信道而言,除了Cod4 和Cod12 方法外,其他几种方案的NMSE 性能最大差距分别为0.33 dB和0.44 dB。

图1 12 径COST207 信道模型下不同方案的NMSE 曲线图

图2 6 径Vehicular 信道模型下不同方案的NMSE 曲线

其次,对两种信道下各种方案的误码率(bit error ratio,BER)进行仿真分析,仿真结果如图3 和图4所示。

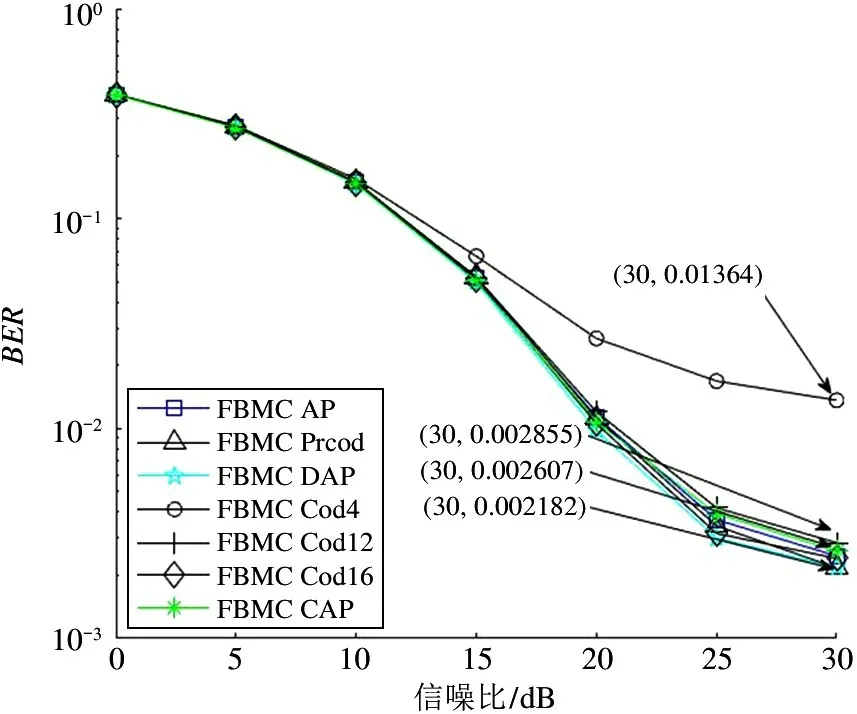
图3 12 径COST207 信道模型下不同方案的BER 曲线

可以看出,误码率性能和归一化均方误差性能对应,对于COST207 和Vehicular 信道而言,除了Cod4 和Cod12 方法外,其他几种方案误码率之间的最大差距分别为0.773 dB 和2.431 dB。

从图1～图4 中数据可以得出,在频率选择性信道下,相对于纯4 编码方案,在结合了所提Prod 的4编码方案在COST207 和Vehicular 两种信道下的归一化均方误差分别降低了4.63 dB 和10.74 dB左右,而误码率性则分别降低了7.96 dB 和25.25 dB 左右。

图4 6 径Vehicular 信道模型下不同方案的BER 曲线

最后,对本文方案在双选信道下的误码率性能进行仿真,仿真结果如图5 所示。

图5 12 径COST207 信道模型下移动台速度为500 km/h 时不同方案的BER 曲线

可以看出,当移动台相对速度为500 km/h 时,受多普勒频移影响,信道估计和误码率性能均有大幅降低,但是相对于其他方案,二者性能依然达到近似一致的效果,相对于4 编码方案,本文方案误码率性能提高了1.7733 dB。

综合图1～图5 不难发现,对于编码法而言,编码数目和信道估计的准确性有直接关系,尤其是在大于12 位编码后其精度的小幅改变是以增加大量计算复杂度为代价的。对比4 编码位的纯编码方案,Procd 乘法计算复杂度增加了16 +36 -3 ×4 ×2=28 次。而作为对比的Cod16 编码方案则增加了16 ×15 ×2 -3 ×4 ×2=456 次。另外AP 法由于只需对式(8)进行求解,因此消耗复杂度为N=16 次,对于其改进算法DAP,同样只需额外消耗N=16 次乘法;采用4 编码的CAP 的计算复杂度则是编码法和AP 法复杂度的叠加,即12 +3 ×4 ×2=36 次。虽然AP 的改进算法复杂度均低于Prod,但所提方案将干扰进行归类,简化了FBMC 系统信道估计对未知数据的处理,降低了传统方案的使用标准,并且增加少量复杂度换来的是传输效率的提高,除了中心导频外只额外损耗1 个有效数据位,这一方面提高了传输效率,另一方面也增加了离散导频方案信道估计的可操作性。当Prod 继续结合干扰利用法时,在保持和CAP、DAP 同样的传输效率的前提下,会进一步改善误码率性能[7]。

5 结论

本文通过对FBMC 导频周围符号进行预先处理,将FBMC 信道估计中的导频所受未知数据符号干扰问题成功转化到对极少数干扰的处理上,简化了FBMC 信道估计问题。理论分析和仿真结果表明,该方案可以和编码法很好地结合,降低了其计算复杂度,使得在理论上无法直接应用的编码方案得到很好的应用。对比双辅助导频法、编码辅助导频法等改进算法,本文方案相对于传统编码和辅助导频方案无需额外的频谱损耗,可以实现频谱资源的高效利用。