基于随机森林算法的对冲锅炉出口NOx 排放量预测模型研究

王伟同，范海东，梁成思，赵中阳，邵宇浩，谭畅，郑成航

（1.浙江大学能源清洁利用国家重点实验室，国家环境保护燃煤大气污染控制工程技术中心，浙江 杭州 310027；2.浙江浙能技术研究院有限公司，浙江 杭州 311121）

国家能源局统计显示，2020 年我国全年能源消费总量49.8 亿t 标准煤，其中煤炭消费占能源消费总量的56.8%[1]。由于我国具有“富煤、贫油、少气”的资源特点约束，能源消费结构将长期以煤炭消费为主[2]。煤炭燃烧后会产生多种污染物，包括NOx、硫化物和烟尘等，对人们的生产生活产生巨大的影响[3-7]。因此，我国对于燃煤电站NOx排放治理的要求趋于严格，排放指标相比于欧盟燃煤电厂排放指标更严格[8-9]。

通过烟气脱硝系统对NOx排放进行控制是燃煤电厂NOx超低排放的主要方式。然而针对控制程序的调整依赖于仪器仪表测量的数据，这些仪器测量的数据具有滞后性，使得控制作用始终落后于被控变量，尤其在锅炉工况变化较大的时候，滞后所产生的影响更大。所以需要建立快速、准确的对冲锅炉出口NOx排放量的预测模型，以便对仪器的测量数据进行修正，为对冲锅炉NOx控制系统提前应对不同工况提供模型基础。

对冲锅炉的燃烧系统的运行数据具有种类多、维度高和生成速度快等特点，并且其中NOx生成受到诸多因素（如二次风量、燃烧器给煤量、燃烧温度等）的影响，这些特征之间耦合程度较高，导致在海量数据中寻找出锅炉NOx排放量与锅炉特征之间的联系较为困难。如何快速并准确地提前预测对冲锅炉出口NOx的排放量，成为摆在研究者面前的一个挑战。

机器学习是对锅炉出口NOx排放量进行预测的一种有效方法。支持向量机、BP 神经网络、逻辑回归以及以它们为基础改进后的算法曾先后用于排放量的预测。刘飞明、张雨飞将支持向量机与改进混沌粒子群算法相结合来对NOx排放量进行在线建模[10]，丁知平和李应保等采用改进的最小二乘支持向量机建立煤粉锅炉NOx排放模型[11-12]。但在缺失数据的情况下，支持向量机会变得十分敏感，影响输出结果。在复杂的特征以及大量数据下这些单分类器模型并不能在NOx排放量预测上取得良好的效果。刘博文[13]使用RNN 算法建立脱硝系统入口NOx质量浓度测量修正方法，通过提前预测脱硝系统入口处NOx质量浓度测量值，使烟气排放连续监测系统测量滞后误差降低了32.6%；徐凯等[14]使用神经网络针对循环流化床锅炉建立自适应控制模型；印江等[15]使用IPSO-BP 算法针对NOx排放量进行预测。虽然神经网络在预测数据较为稳定时具有较高的精度，但存在网络结构难以确定、学习速度慢及易陷入局部最优等问题。

随机森林（random forest，RF）是一种分类和预测集成的学习算法。通过多轮抽样，生成k个数据集并构成含有k棵决策树的随机森林，其随机性使得模型不易陷入过拟合并降低敏感数据对模型预测结果的影响，在不同的领域取得了不错的效果。赵腾等[16]采用随机森林算法针对用电差异性带来的电量预测问题进行建模，在135 维的数据集下建立的模型平均百分比误差（mean absolute percentage error，MAPE）为1.84。魏勤等[17]使用随机森林预测电力现货市场的出清价格，较相同条件下的决策树（classification and regression tree，CART）、SVR 和ANN 算法建立的预测模型平均误差分别相对减少了35.2%、25.3%和26.0%。

此外，根据文献[18-19]可知，对大数据进行回归预测时，应减少数据的复杂程度以及降低无关变量因素对模型预测的影响，因此需要建立初始指标体系进行特征筛选，将筛选完成后的特征放入随机森林中进行训练得出结果。Žmuk Berislav等[20]对相关性系数进行了详尽的描述。相关性系数是用来判断2 个特征之间是否具有相关的关系以及其关系的强弱程度。由于锅炉燃烧系统的数据具有强非线性，所以选择适用于非线性数据的Spearman 系数作为特征选择方法。

综上所述，为了得到一种兼具通用性和有效性的NOx排放量预测方法，本文在原有的随机森林回归算法基础上，与Spearman 系数特征选择相结合。首先利用Spearman 系数进行锅炉燃烧特征筛选，选择出与NOx排放量相关性强的特征，并将无关特征删除；利用筛选出的特征搭建基于随机森林算法的NOx排放量预测模型；使用决定系数（determination coefficient，R2）、均方根误差（root mean square error，δRMSE）模型性能指标对比并分析基于Spearman 系数的随机森林算法与其他模型的预测效果。

1 建模理论及对象描述

1.1 Spearman 系数原理

Spearman 相关性系数用于描述特征与其响应变量之间的关系，其值介于-1～1。数值的绝对值越大，变量之间的相关性程度也就越大。Spearman 系数为正值的时候，表示正相关；为负值的时候，表示为负相关。如果数据集为P={A,B,...,X,Y}，其中X={X1,X2...,Xn}，Y={Y1,Y2...,Yn}，计算两者Spearman 系数的公式为：

式中：X代表X变量，而Y代表Y变量；Xi、Yi代表X和Y中的第i个数据；μX、μY代表X、Y变量的平均值。

1.2 决策树原理

决策树是一种既可以处理分类问题，也可以处理回归问题的改进型单分类回归器的学习算法。

决策树算法作用于回归的时候，使用Variance方差来对节点进行分裂，对训练集的输入划分空间，不断地将样本数据分裂到不同的节点空间。每个节点会得到1 个预测值，全部节点预测值的平均值就是最终的算法输出结果。每个节点的Variance方差越小，代表该节点所分裂得到的特征重要性越高。假设当前集合为D，样本数量为N，每个样本的值为yi，Variance 方差的计算式为：

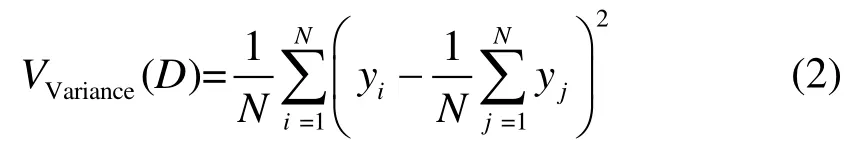
1.3 随机森林结构原理

随机森林是随机创造的决策树组成的森林。决策树中的每个节点是特征的1 个随机子集，用于计算输出。随机森林将单个决策树的输出整合起来生成最后的输出结果，其结构如图1 所示。

图1 随机森林回归算法结构Fig.1 Structure of the random forest regression algorithm

方匡南等[21]对随机森林算法进行研究，发现随机森林相较于传统的机器学习模型具有训练速度快、预测效果好、泛化能力强、鲁棒性强等优势，可有效避免模型过拟合的现象，适用于高维数据的处理。

随机森林主要是采用bootstrap 对数据集进行随机抽样，抽取出n个子数据集，并从子数据集的所有特征中选取m个特征用于每个节点的分割。m是一个预定义的数字。随机森林会找到每棵树的最佳分割点，其余部分类似决策树，最后对于所有枝点的预测值进行平均即得到最终的预测值。

尽管随机森林具有很多优势，但其在构建过程中考虑到所有的输入维度，划分不同的维度区间，当所划分得到的随机森林中决策树棵数很多的时候，训练所需的时间和空间成本会很大。因此使用Spearman 系数将无关输入进行删减并利用评价指标对模型参数进行调整，使得模型训练所花费的时间尽可能缩减。

1.4 对象描述

本文主要围绕对冲锅炉的历史数据构建模型。对冲锅炉结构及测点布置如图2 所示。

图2 对冲锅炉测点布置Fig.2 Measuring point diagram of hedge boiler

对冲锅炉采用前后墙对冲的燃烧方式，在锅炉前后墙各布置3 层燃烧器，燃尽区布置2 层燃尽风，再往上为一次风、二次风以及烟气流量、机组负荷的测点，往右为低温过热器、低温再热器、高温再热器以及省煤器的测点。数据从电厂信息（plant information，PI）数据库中采集获得。采样间隔10 s，采样周期3 个月，总共372 704 个数据点组成最初的数据集。数据集中包含低、中、高多个负荷段及升、降、平稳负荷多种运行工况，一定程度上可以覆盖电厂运行典型工况特征。部分数据如图3 所示。

图3 对冲锅炉数据集部分数据Fig.3 Partial data of the hedge boiler dataset

2 随机森林模型构建流程

图4 为模型构建流程。首先对锅炉数据进行预处理。对2 个数据集进行特征选取，根据Spearman系数或合并或删除多余特征，减少建模时间，并划分为输入特征（如机组负荷、给煤机给煤量等）以及与预测结果对照的真实值（锅炉出口NOx质量浓度）。

图4 模型构建流程Fig.4 Model building flowchart

将t时间段的输入特征（图4 中红色区域）输入随机森林模型，用预测得到的t+m时间段输出与原t+m时间段的数据进行对比来分析模型预测效果。根据燃煤电厂半个月内的数据来预测未来的NOx质量浓度，将t设置为15 天。由于电厂NOx测量表的延迟约为6 min，所以将m设置为6 min。

2.1 数据预处理

针对对冲锅炉数据进行预处理，采用粗大值剔除、吹扫过程处理、数据平滑处理3 个方面的处理，如图5 所示。

图5 锅炉出口NOx 排放量数据处理Fig.5 Processing of the NOx data at the boiler outlet

1）剔除数据中的粗大值并采用线性插值方法对吹扫过程数据进行处理：

式中：x1为吹扫开始时质量浓度；xm+1为吹扫结束后的质量浓度；xi为吹扫处理后时间i的质量浓度。

2）对数据进行平滑处理，数据采集过程存在一定的噪声，高斯滤波可以有效抑制噪声的影响。

2.2 特征选取

数据集中的特征包括机组负荷、主蒸汽压力、总风量、燃尽风、一次风、二次风、给煤机风量、省煤器出口烟温、烟气流量、给煤机给煤指令、各层燃烧器壁温、各燃烧器一次风速和主蒸汽温度等特征。

利用Spearman 相关系数针对特征之间的相关性进行分析，其相关性系数绝对值越接近1，特征之间的相关性越高。可合并一些相关性较高的特征，并去掉一些与NOx排放量相关性较弱的特征变量。锅炉特征之间的相关性热图如图6 所示，特征与NOx排放量之间的Spearman 系数结果见表1。

但她始终没有生下一儿半女，和家世显赫、儿女双全的王夫人相比，处处都相形见绌。所以即便身为长房媳妇，却时时被二房压了一头。

表1 特征与NOx 质量浓度之间的Spearman 系数Tab.1 Spearman coefficient between characteristic and NOx

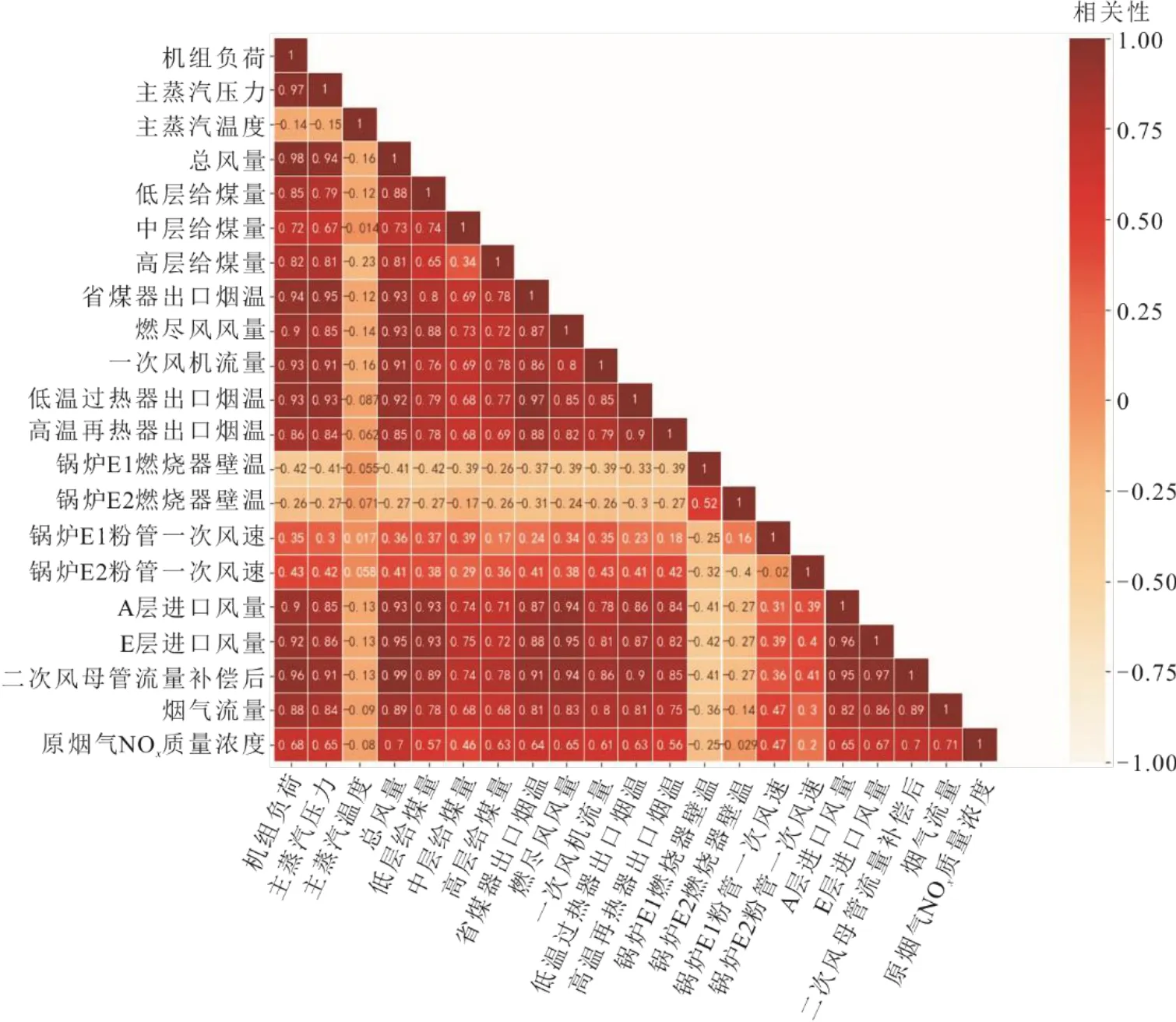
图6 锅炉参数相关性热图Fig.6 Boiler parameter correlation heat map

通过相关性热图可以发现：总风量和其他风量之间的相关性较高，考虑到每层的风量对于对冲燃烧的影响力不一样，所以选用各层给风量；同时过热器、再热器以及省煤器的温度之间的相关性均超过0.9，根据其和NOx排放量的相关性从三者中选取省煤器出口烟温作为输入特征。

最终选取机组负荷X1、主蒸汽压力X2、燃尽风X3、一次风X4、二次风X5、给煤机风量X6—X11、省煤器出口烟温X12、烟气流量X13、给煤机给煤量X14—X19总计19 维作为模型的输入特征，锅炉NOx质量浓度作为模型的输出特征。

选取数据处理后的200 000 个数据点，根据模型验证的思路，将其中190 000 个数据作为训练集输入模型，剩余的数据作为测试集。

2.3 模型评价指标及模型参数设置

为了评价模型的NOx排放预测性能，引入均方根误差δRMSE和决定系数R22 个指标。δRMSE反映了NOx质量浓度预测值与真实值之间的偏差。δRMSE越小，模型预测效果越好。R2反映了NOx质量浓度的变化能通过预测模型被选取的特征解释的比例。R2越接近于1，说明模型拟合效果越好。

在经过数据预处理以及特征参数选取之后，划分成输入特征与输出对照真实值，之后预设随机森林参数，将训练集输入随机森林模型进行训练，并以2 000 个点为一个时间段观察模型预测效果。表2 为随机森林预测模型参数。

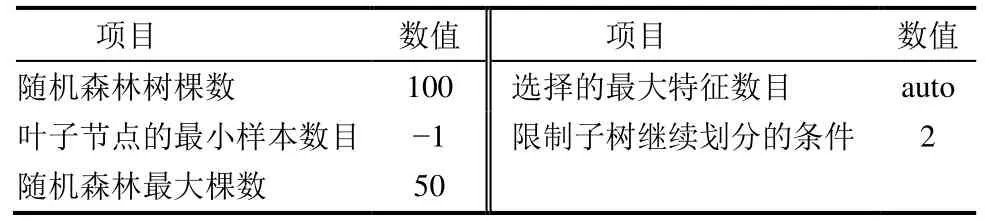
表2 随机森林预测模型参数Tab.2 Parameters of Stochastic Forest prediction model

3 结果与分析

3.1 模型预测结果

为了调整随机森林模型的棵数让模型更为快速精确，使用前向搜索方法寻找最优棵数。每个步骤树集的拟合性能由δRMSE和R2评估，结果如图7所示。综合建模时间以及预测精度的考量，决定由60 棵决策树构建最终的NOx排放量预测模型。预测结果的整体均方根误差为8.716 mg/m3，决定系数为0.93。训练集NOx排放量快速变化和平稳期以及不同负荷段NOx排放量预测如图8、图9 所示。

图7 随机森林棵数参数调整Fig.7 Parameter adjustment of random forest number

图8 训练集NOx 排放量快速变化及平稳期Fig.8 The rapidly and stationary period of NOx changes in training set

图9 训练集不同负荷段NOx 排放量预测Fig.9 NOx prediction in different load segments of training set:low load,medium load,high load

3.2 模型对比分析

为了验证以训练集为基础建立的随机森林模型的泛化效果，使用RF、SVR、PCR 以及KNN[22-25]4 种模型在总计10 000 个数据点的测试集上进行NOx排放量预测，最后进行效果对比，得到多模型预测散点图如图10 所示。图10 中黑线代表预测值等于实际值。数据点偏离参考线的距离越近、数量越多，代表模型的预测结果越理想。由图10 可以看出，随机森林（RF）在预测集的效果最为精确，SVR和PCR 的预测效果次于随机森林，KNN 模型的预测效果最差。

图10 多模型预测散点图Fig.10 Multi-model prediction scatter plot

表3 为多模型评价指标和模型计算耗时。从表3 可以看出，随机森林模型在模型计算时间短的情况下兼具更高的精确度和泛化能力。

表3 多模型评价指标和模型计算耗时Tab.3 Multi-model evaluation index and model calculation time-consuming

图11 为4 种模型在测试集的误差分布。由图11可见：随机森林模型和SVR 模型的误差分布曲线相比于PCR 与KNN 模型更加集中；KNN 模型预测误差绝对值出现在30 mg/m3以上的频次较高，在实际过程中可能经常出现模型失配现象；而随机森林模型相较于SVR 模型更集中于-10～10 mg/m3，所以其预测更为准确，更加适应NOx质量浓度预测的各种情况。

图11 模型在测试集的误差分布Fig.11 Error distribution diagram of models in the test set

图12 为测试集中NOx质量浓度在不断变化时候，4 种模型的预测效果图以及放大图。由图12 可见：随机森林预测模型在平稳期的预测效果和其他模型相差不大，但在NOx质量浓度变化剧烈的过程中，如快速下降以及快速上升2 个过程中，都对出口NOx排放量有较为准确的预测；相较于其他模型，随机森林模型能更好地对NOx排放量变化趋势进行适应并预测。

图12 NOx 排放量变化时模型效果以及放大图Fig.12 Model rendering when NOx emission changes

4 结论

本文以燃煤电厂对冲锅炉的运行数据为基础，利用随机森林算法泛化性强、建模时间短的特性，并辅以Spearman 系数方法去除无关特征，降低无关特征对模型精度的影响，建立了随机森林模型来预测锅炉出口的NOx质量浓度，以提前了解对冲锅炉出口NOx排放量的变化趋势，并与SVR、PCR 及KNN 3 种模型进行了预测精度的对比。研究结果表明：

1）基于Spearman 的随机森林模型在测试集上的预测结果的均方根误差为10.182 mg/m3，决定系数为0.913，优于另外3 种模型，并且其在模型计算耗时上的表现体现了随机森林在处理高维度数据、大规模非线性问题上的优越性。

2）基于Spearman 的随机森林模型预测误差集中在-10～10 mg/m3的范围内，所以采用基于Spearman的随机森林模型可以快速而准确地提前预测锅炉NOx排放量的变化趋势。

火电厂控制系统数据的海量化和高维化是电厂发展的必然趋势，而数据时滞的存在使得控制作用落后于控制对象，所以利用控制系统的数据对控制对象的未来的变化趋势进行预测是十分有必要的。本文对随机森林的研究可应用于对控制对象的变化趋势的预测。