一道研究生入学考试题的思考

高巧琴

(吕梁学院 数学系， 山西 离石 033001)

0 引言

数学分析的研究对象是函数，主要研究函数的三大分析性质：连续性、可微性与可积性，而极限是研究它们的主要工具，是贯穿数学分析的一条主线.因此,掌握好极限的求解方法是学习数学分析的关键环节.极限包含数列极限与函数极限，二者是特殊与一般关系，要掌握求极限的方法，首先从最基本的数列极限开始.

求数列极限的方法繁多，学生碰到这类问题时常常会出现对方法选择的困惑.以南京师范大学2017年研究生入学考试数学分析第一题的一道数列极限为例，分析探讨学生易出现的误区及合理选择正确方法求解数列极限.

试题计算极限：

笔者针对这道题目的解法分析，探讨在教学中如何打破学生的定势思维和培养学生的创新思维能力.

1 解法分析

很多同学首先想到利用迫敛性求解：

因为

(1)

这样的解法是错误的，错在哪里呢？

可以看出，对于所有的n并不是单调的，而是从第三项开始是严格单调递减的，如图1所示.

图1 数列的图像

结构分析这属于数列极限问题，从形式上看，是关于n项和的极限，但不能直接应用数列极限的四则运算法则，因为随着n的增大数列项数不断增加，而四则运算法则只适用于有限个数列的和，鉴于此，常规的思路是先求和再求极限.

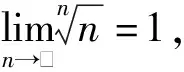
方法1：(利用均值极限)

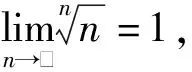
方法2：(利用施笃兹定理)

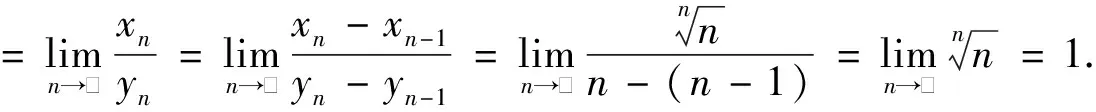
2 几点反思

2.1 教师在教学过程中，一方面要注重基本概念的解析、基本理论的拓展、基本方法的使用、典型错误的剖析；另一方面，要打破学生的思维定势，全方位考虑问题，可以培养学生的探索精神，提高学生解决问题的能力和创新思维能力[3].

2.2 学生在学习过程中，要研究各种解题方法的原理本质，总结在解题过程中容易出现的误区，注意知识的严谨性，学会全面分析解决问题的能力.