首次积分法求变系数(3+1)维非线性薛定谔方程的精确解
2022-04-29欧阳坦
欧阳坦,肖 冰
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
物理学、生物学、化学、力学、生物医学、通信工程、图像处理等许多领域的问题通过数学建模都可以归结为非线性偏微分方程的相关问题。因此,研究非线性偏微分方程的精确解[1-5]有助于更好地处理以上问题。目前,许多求解非线性微分方程精确解的有效方法已经被证明,如指数函数法[6],齐次平衡法[7],双曲正切法[8],Jacobi椭圆函数展开法[9]等。
肖婷婷[10]用Jacobi 椭圆函数展开法求出了1 维薛定谔方程的精确解,杜玲禧等[11]用符号运算方法求出了广义非线性薛定谔方程的精确解,张清梅等[12]用首次积分法[13]求出了广义非线性薛定谔方程和高阶色散非线性薛定谔方程的精确解,何晓莹等[14]用首次积分法求出了(2+1)维非线性薛定谔方程。基于以上研究,文章运用首次积分方法来求解变系数(3+1)维非线性薛定谔方程[15]。
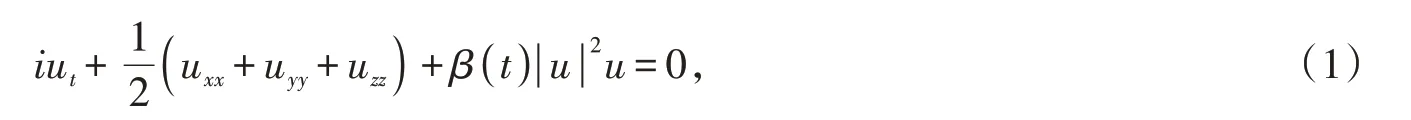
它描述的是空间孤子在克尔介质中的传输特性且系数随时间而变换,在直角坐标系中的归一化形式,u(x,y,z)是孤波波包,t 为归一化传输时间;β(t)是克尔非线性系数,当β(t)>0 时是自聚焦非线性介质,当β(t)<0 时是自散焦非线性介质。当(1)在一维的情况下,它描述的是光孤子在单模光纤中的传输规律[16]。求解方程(1)的精确解具有非常重要的意义,可以洞察这些物理现象的本质,非线性薛定谔方程可以解释光脉冲在色散和非线性介质中的传输,可以讨论非线性光学的自陷现象。
1 首次积分方法的介绍
对于一个非线性偏微分方程:


再引入一个新的独立变量X( ξ )=U( ξ ),Y( ξ )=U( ξ ),则(2)等价于常微分方程组

由常微分方程的定性理论可知,若能找到首次积分,常微分方程组就能通过除法定理得到它的解。
除法定理:假设P( w,z ),Q( w,z )是复数域C[ w,z ]上的多项式,并且P( w,z )是复数域C[ w,z ]上的不可约多项式,如果P( w,z )的所有零点也是Q( w,z )的零点,那么在复数域上存在一个多项式Q[ w,z ]使得Q[ w,z ]=P[ w,z ]G[ w,z ].
2 变系数(3+1)维非线性薛定谔方程的精确解
假设(1)有如下形式的行波解
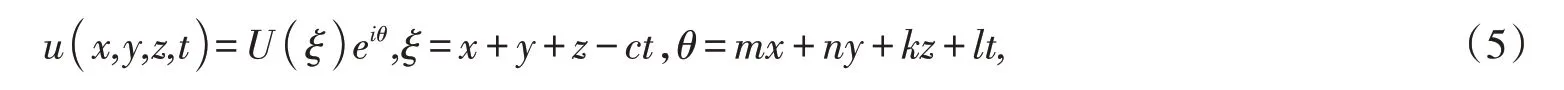
将(5)代入(1)得
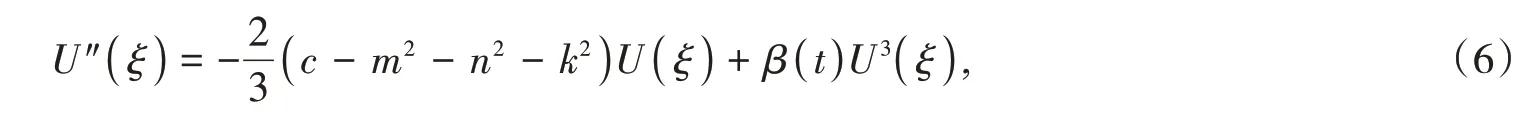
令X(ξ )=U(ξ ),Y(ξ )=Uξ(ξ ),则方程(6)等价于

依照首次积分方法,假设X( ξ ),Y( ξ )是(7)的非平凡解,则在复数域C上存在不可约多项式
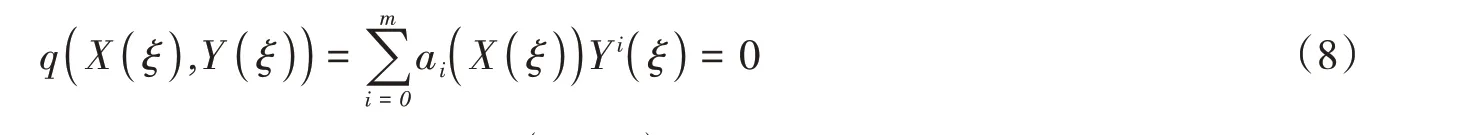
其中,ai( X( ξ ))( i=0,1,…,m )是关于X( ξ )的多项式,且am( X( ξ ))≠0(,8)为(7)的首次积分。由除法定理可知,在复数域C上存在多项式g( X )+h( X )Y满足
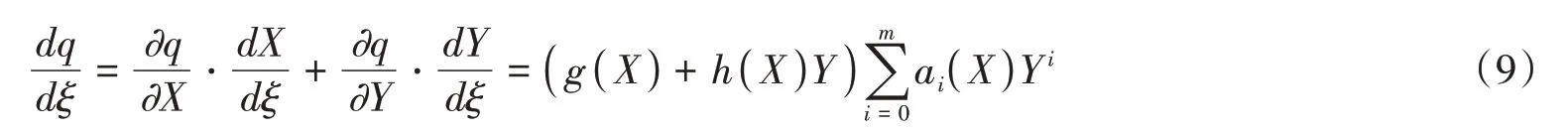
情形1 考虑m=1,则(8)变为

将(10)代入(9)后比较等式两边Yi( i=0,1) 的系数得
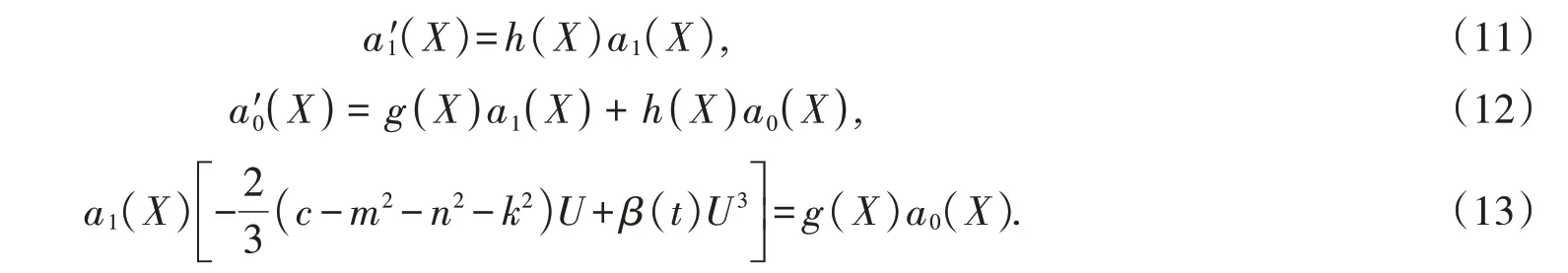
由(11)可知a1( X )为一个常数且h( X )= 0.为了运算的简便不妨假设a1( X )= 1,通过平衡a0( X )和g( X)的系数,可得deg=2.则令g( X )=AX+B,可得a0( X )=AX2+BX+D,其中D 为积分常数。将a0( X )代入(13),并使Xi两边的系数相等,可得

将(14)代入(8)得

将(16)代入(7)得

其中,ξ0为任意常数。
所以,可以得到(1)的精确解
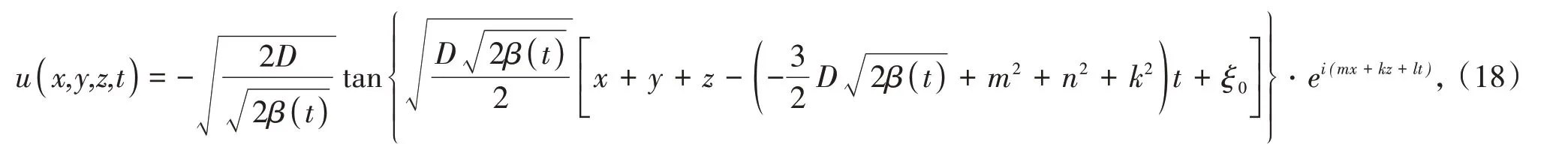
同理,将(15)代入(8)得

将(19)代入(7)得

其中ξ0为任意常数。
所以,可得(1)的精确解
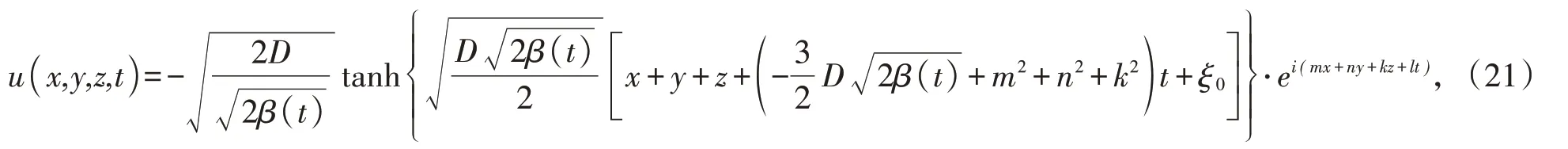
情形2 考虑m = 2的情形,则(8)变为
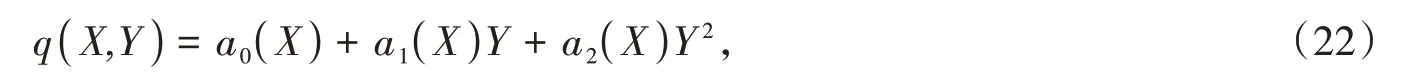
将(22)代入(9)后比较等式两边Yi( i=0,1,2 )的系数得

由(23)可知a2( X )为一个常数且h( X )=0.为了运算的简便不妨假设a2( X )=1,通过平衡a0( X ),a1( X ),g( X )的系数,可得deg[ g( X )]=1,deg[ a1( X )]=2,deg[ a0( X )]=4。则令g( X )=AX+B,可得
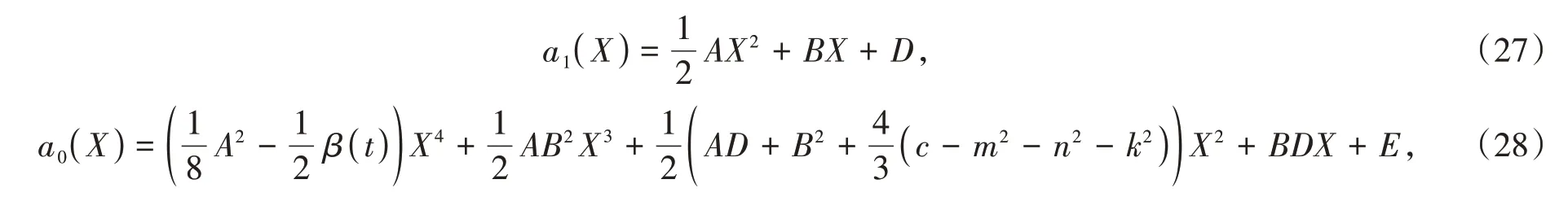
其中E 为积分常数。将a0( X ),a1( X ),g( X )代入(26),并使Xi两边的系数相等,可得

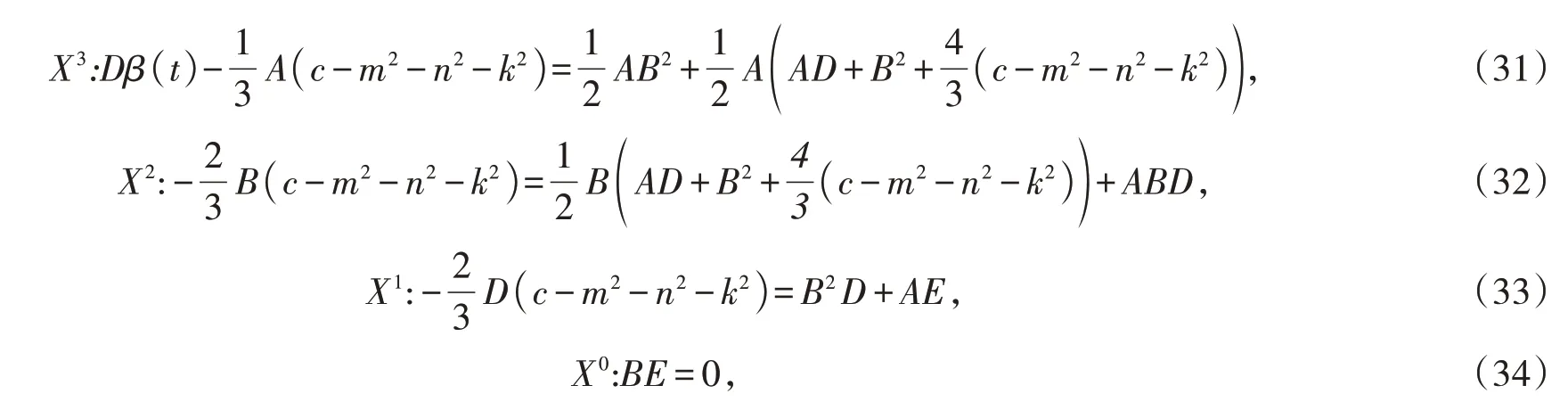
解方程(29)至(34),可得
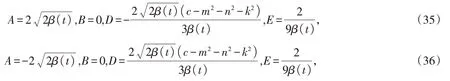
将其解(35)代入(27),(28)得
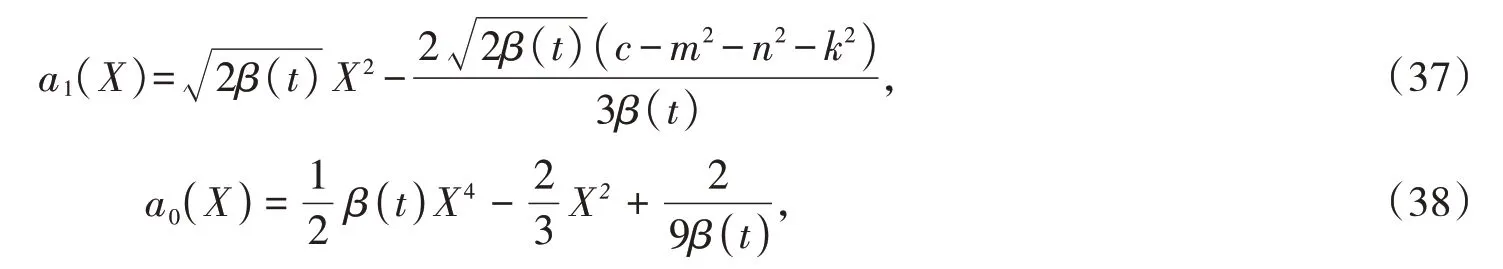
将(37),(38)代入(8)得,

解(39)可得
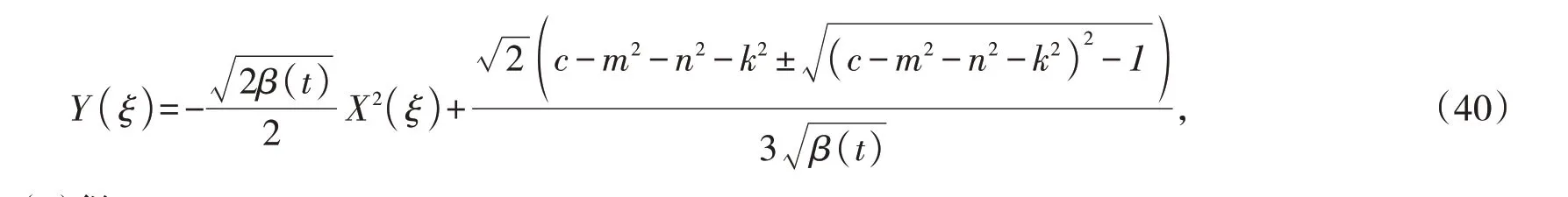
将(40)代入(7)得
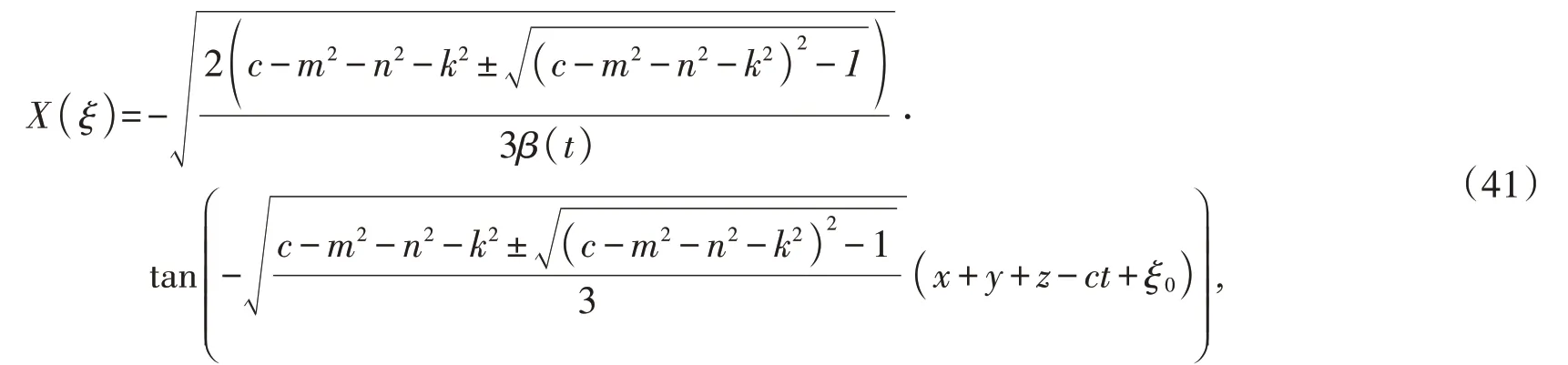
其中,ξ0为任意常数。
所以,得到(1)精确解
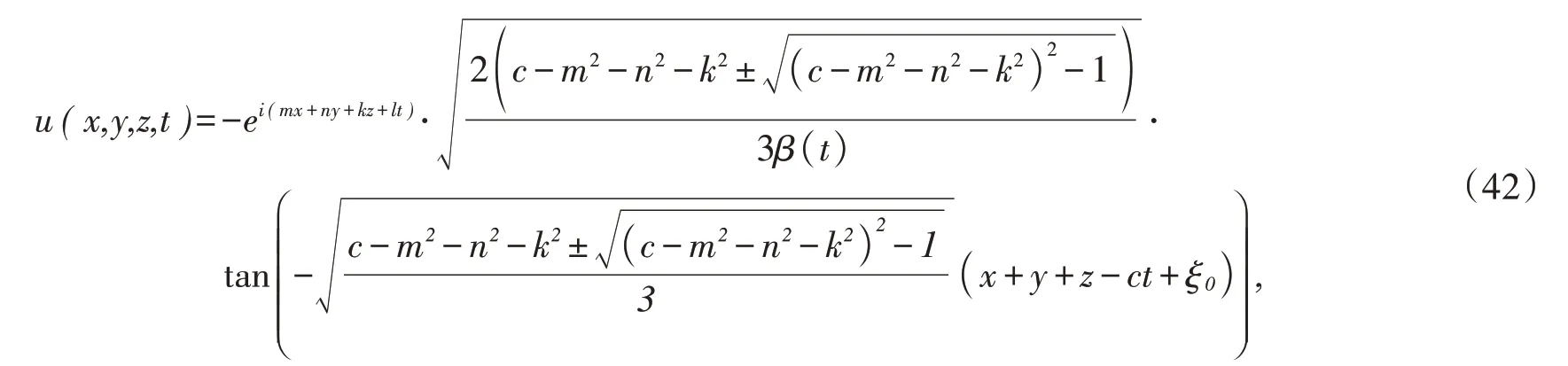
同理,将(36)代入代入(27),(28)得
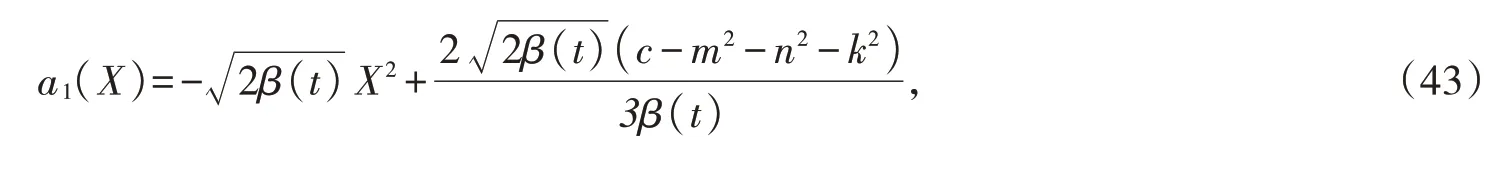
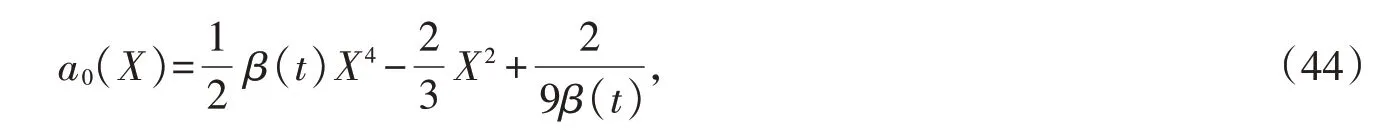
将(43),(44)代入(8)得,
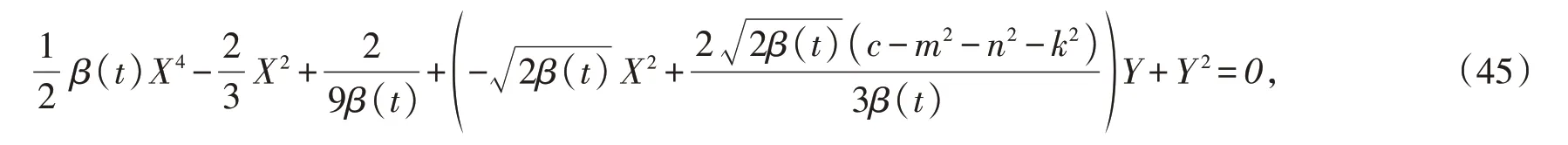
解(45)可得

将(46)代入(7)得
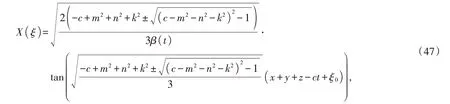
其中,ξ0为任意常数。
所以,可得(1)的精确解

结论
文章在交换代数的环理论的基础上,应用首次积分法,通过计算得到了在m=1 和m=2 的情形下变系数(3+1)维非线性薛定谔方程的精确解,当m=1 时,精确解为(18)和(21),当m=2 时,精确解为(42)和(48),并且这些都是新的方法的精确解。首次积分方法在求解变系数(3+1)维非线性薛定谔方程时,是具有可行性的,可以将之用于求解条件更广泛的非线性数学物理方程。
