数据压缩与人工智能的数学研究
2022-04-29曾福庚
张 阳,曾福庚
(1.中国科学院中科建设 山东东润清洁能源有限公司,山东 东营 257000;2.贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550000)
生活中任何地方都可以看到各种各样的信息,例如,信息收集、处理、存储、共享等。过去、现在和未来的信息和数据量庞大,没有任何实体或组织能够完全存储如此大量的数据,只可以存储数据的相关部分进行检索和传输,以便必要时交换和使用网络中的数据。然而,随着数据的积累,网络访问量的增加将会占用较多时间和带宽。为提高数据传输速度,缩短网络访问时间,最直接的方法就是扩大网络带宽。但是,网络的频率范围将受到限制,收集的数据越多,无法存储的数据就越多。有效的数据压缩可以解决这个问题。
目前,数据压缩主要分为两类,一类是有损压缩,主要用于压缩音频、视频、图形和图像。其主要特点是数据压缩率一般在10:1到30:1之间;另一类是无损压缩,用于压缩文本文档、数据库、程序等。最大压缩率约为70%(通常为50%-60%)。两种压缩率低的原因是,当前的无损压缩算法在文件中要找到相同的副本;可执行程序(EXE、com 等)压缩率只能达到几个百分点;有损压缩不仅减少了图像数据量,而且影响了图像质量。因此,寻找一种更有效的方法来提高数据压缩率非常重要。
文章创建了一个新的通用数据模型,研究目的是:在现实世界中创造某种类型的对象(例如,将图像清晰度划分为低级像素340×255分辨率、普通像素720×570分辨率、高清像素1920×1080分辨率、4K像素3840×2160 分辨率和8K 像素7680×4320 分辨率,用于分层研究),并在此基础上描述属性,实现了现实世界中的数据压缩和分析功能;分类对象的压缩数据模型基于统一的数据描述模型,它提供了现实世界中对象压缩数据模型的高度一致性;纵向时间分割与对象单元的横向分层相结合。因此,使用简化的逻辑和数学公式来表示不同数据压缩结构的拓扑结构是研究和分析压缩模型的一种新方法。复杂且难以表达的模型拓扑中的层次逻辑关系[1-9]用于表示压缩拓扑[10-11]。揭示数据压缩有序结构关系,优化压缩模型,改进压缩布局和分层管理,对于人工智能[12]机器学习为模型提供理论和算法保障,使其更有效、方便、安全,面向云计算的数据压缩网络。
1 数据压缩数学模型的建立
在ESTDM 模型[13]中,将时间视为跨越过去和未来的无限时间,具有普遍性、连续性、可测量性和单向性。对象现象发生变化称为事件,时间序列称为时间列表。关于ESTDM 模型的许多资料已经过详细描述,在此不再赘述(图1)。
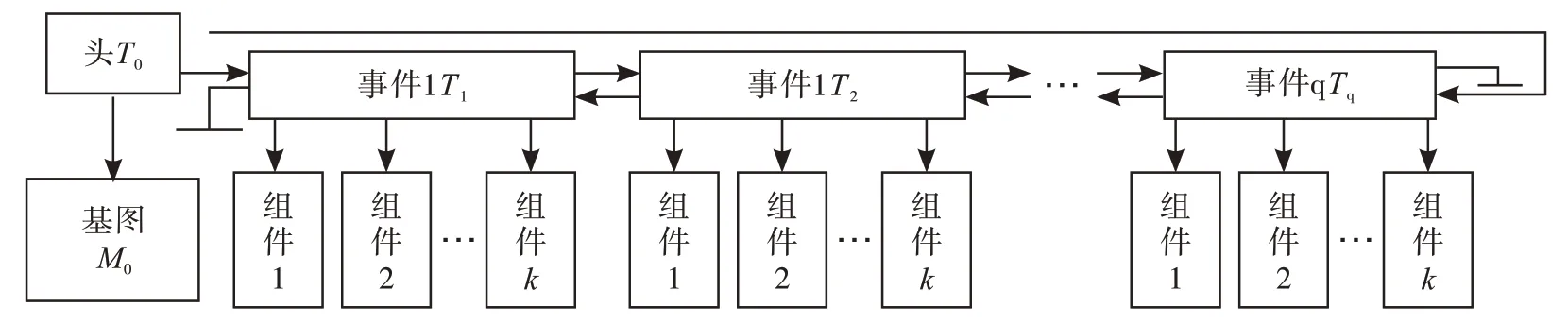
图1 基于事件的数据模型
将事件层次结构转换为压?缩拓扑[10-11](图2)。

图2 事件的层次嵌套结构拓扑
图2用以下公式表示为数学模型。
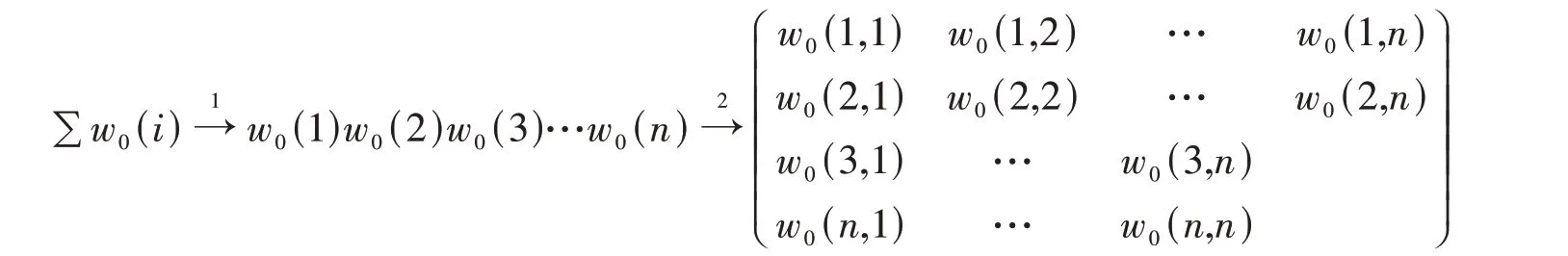

计算第一层数据压缩模型的数学公式

式中:∑w0(i)表示w0数据压缩网络所有点的集合;w0(i)(i=1,2,…,n)表示w0数据压缩网络第i 个点;“→1”表示数据压缩1层的等式对应包含关系,“1”表示在第一层上,“→”表示等于,箭头表示从属关系,两个加在一起读作“一层数据压缩等于”。w0表示时间维度下数据压缩点名称,n是点的序号。
第二层数据压缩的数学公式由公式(1)导出。

第n层数据压缩的数学公式由公式(2)导出。

注:w0(i,…,i)为n层所有点的集数
由式(1-3)推导全架构数据压缩模型的数学公式为:
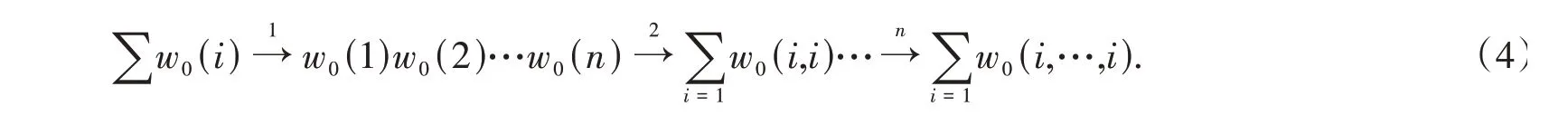
从图1中基于事件的数据模型中,得到图3中数据压缩的数学模型:

图3 数据压缩模型
最终得到数据压缩模型的数学公式

设:

代入公式(5),最终得到数据压缩模型的数学公式

M0为压缩原始数据;T1为数据事件1;T2为数据事件2;Tq为数据事件q;t1为时段1;t2为时段2;tq为时段q.
2 数据压缩模型的计算
2.1 数据压缩模型的逻辑地址
存储在地址中的压缩数据和现有的寻址方法非常复杂。主要有两种类型:一种按主要行为规则的顺序存储,另一种是基于列控制的顺序存储。这两种类型的排序顺序非常复杂,难以表达。采用数据压缩模型表示数学地址,相对清晰简单。
图2在数据压缩模型四层点w0(2,1,1,2)数学逻辑地址表示式如下:
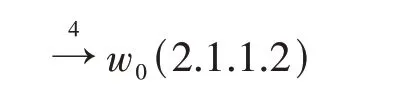
数据压缩数学逻辑地址公式为:

2.2 数据压缩数学模型的分解与合并公式
数据压缩模型通常需要减少或增加点。图4是第1层数据缩减拓扑图。
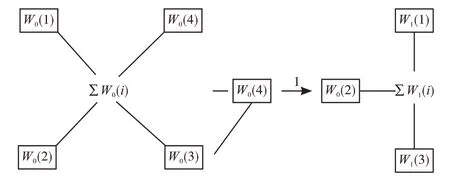
图4 一层数据压缩模型缩减拓扑逻辑图
数据缩减点的数据公式推导如下:

对应的,单层数据增加一个点的数据推导的结果为:

同理,可推导多层数据的分解和合并模型:
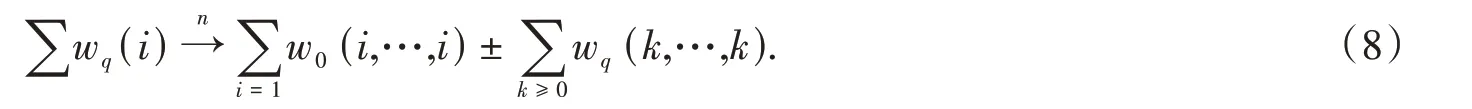
其中:k(k≥0)为所有层可增减数据集数。

设:

M0为压缩原始数据;Tq为wq事件数据。
2.3 数据压缩数学模型的乘法推导公式
数据压缩数学模型的乘法公式是根据数据压缩数学模型的加减法推导出来的。

注:数学模型矩阵的加法、减法和乘法只对应于原始地址数据的加法、减法和乘法。
2.4 数据压缩数学模型的特征向量和特征值
由于数据压缩数学模型乘法公式是数据压缩模型缩放旋转扭曲,公式(10)具有特征向量与特征值性质,所以数据压缩特征值即数据压缩数学模型乘法公式变为

2.5 压缩值定理
将数据压缩特征值简称压缩值,在某t时刻或时间段,由公式(11)简化如下

压缩值定理:在给定的时间或时间内,压缩值与压缩原始数据成反比,与事件数据成正比。

根据压缩值定理,压缩后的数据会随着时间的推移进行缩减。除了在真实世界中保持原始状态外,其他各点均存储变化部分,以便通过将压缩值与原始数据相乘来修改所表示的数据(图5)。

图5 某部分高清图像变化数据模型
将压缩值定理代入图5得


数据压缩后得

得压缩数据解压后数据

图5可由下式表示

2.6 人工智能在数据压缩模型上的应用
在人工智能神经网络的单层公式中,每层神经元的数目不同,输入输出维数不同,公式中矩阵和向量的行数和列数不同,但形式是一致的。假设考虑的这一层是第i 层,它接受m 个输入,因此该层的计算如下:

式中:xmi是第m 层第i 个神经单元的输出向量,λij是第j 个神经元的特征值,bmj是第j 个神经元对应的偏置值,其中f是一个非线性函数,可见整个神经网络实际上是一个向量到向量的函数。
通过替换数据压缩模型的特征向量和特征值公式(13),得到深度学习时空的数学模型

例如,数据压缩模型图中,用数据压缩人工智能公式应用相似性测度在搜索空间中按照优化准则进行索,寻找最大相关点,用已知参数从而求解出变换模型中匹配数据。通过人工智能将这些因素输入到计算机找到最佳的匹配。
以图3为例,点Wq(2,1,1)与M0原始点匹配有三条路径:
第一条路径:f1=w0(1)→w0(1,2)→w0(1,2,2)
第二条路径:f2=w0(2)→w0(2,1)→w0(2,1,1)
第三条路径:f3=w0(2)→t0(2,2)
由数据压缩典型数据库或模糊数学算出的权重值为:
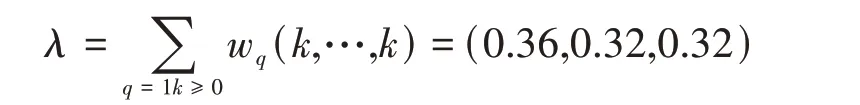
将这三条路径代入数据压缩深度学习公式(16)得到如下式(由于本权重值采用精确值,故偏置向量不必微调数据压缩偏重值,即b=0)得搜,

根据计算,路径f1对总目标的权重为
0.2×0.3+0×0.3+0.7×0.4=0.34
依此类推,得出路径f2、f3对总目标的权值为0.6、0.44.
由此得出f2>f3>f1,f2为最优匹配。
3 结论和展望
文章用数学公式表达了数据压缩模型,并根据压缩值理论给出了数据压缩的逻辑关系。数据压缩值定理可以减少数据存储量,该模型具有较高的数据检索效率,可将对象的变化信息分解为多个片段,并能够完全重建并恢复,具有数据编辑功能(例如,更改每个数据层的颜色灰度压缩值可以在普通LCD 屏幕上生成立体图像)。压缩值还可以二次压缩。数学公式和压缩值可以通过使用时间和各种网络数据库进行扩展。此外,数据可以分类,能够建立一个更完整的数据模型分析系统。
对数据压缩数学的研究发现,数据压缩数学是人工智能、地理信息系统、时空数据库等领域的研究热点。数学数据压缩的未来方向如下:
(1)开发更具适应性的数据压缩理论。也许应放弃原来的数据压缩方法,引入一种新的数据压缩理论,是包含所有压缩数据的统一模型。
(2)作为一种数据压缩结构,它在生物信息学、地理信息系统和语义网络等领域具有重要意义。其研究受到了各个领域学者的高度关注。未来对数据压缩结构的研究将对数据压缩的数学领域做出重要贡献。
(3)数据压缩数学的应用领域已经从地理信息扩展到军事、交通、医学、生物等领域。随着商业信息处理系统(如移动对象数据库)的出现,数据压缩数学的应用前景越来越明显。现有理论成果的推广将是未来数据压缩数学研究的优先方向之一。
(4)人工智能是未来可能对数据压缩产生重大影响的另一个关键因素。信息的压缩程度直接关系到信息的不确定性。假如计算机可以像人类一样猜测后续信息。基于少量已知值,信息被压缩了百分之一甚至百万分之一。因此,高精度、快速压缩的解决方案是必要的,它甚至可能成为目前尚未引起人们注意的巨大市场。使用人工智能进行压缩以满足人工智能的需求是我们的下一个目标。
