不均匀场地钢制波纹接头埋地管线地震响应

王大永， 王星凡， 张煜， 张学杰， 吕杨*

(1.中铁一局集团天津建设工程有限公司， 天津 300250；2.天津城建大学土木工程学院， 天津市土木建筑结构防护与加固重点实验室， 天津 300384)

中外震害调查表明[1-2]，埋地管线主要破坏形式有：接头破坏，如承插式铸铁管道的接头脱出，焊接接头钢管焊缝处开裂，法兰螺栓松动等；管体破坏，如钢筋混凝土管道、石棉水泥管道、铸铁管道等管体出现裂缝，小口径钢管和铸铁管道发生严重锈蚀导致管体发生折断；三通、弯头、闸门和管道与建筑物连接处以及相应连接件，由于应力集中或者运动相位不一致而导致破坏。以上三种破坏形式中接头破坏最普遍，例如，1976年唐山大地震，导致唐山市埋地管线严重破坏，其中供水铸铁管接头破坏率多达79%；日本十胜冲大地震中铸铁管道亦遭受严重破坏，接头拔出占75%左右；1971年，美国圣费尔南多地震，致使地下煤气管道发生严重破坏，给当地居民以及工业生产带来严重的经济损失[3]；1975年，中国海城地震，震级达7.3级，导致营口市埋地管线发生严重损坏，一段长达160 km的埋地管道发生管体折断、接头损坏等多达370处[4]；同时，不均匀场地下埋地管道的震害概率要显著高于均匀场地[5-7]。目前中国对不均匀场地下埋地管线的地震响应规律已经做了很多研究。例如，Hindy等[8]采用平面动应变与静态Mindlin解相结合的方法对埋置于非均匀介质下的管线进行了研究分析，表明管道的应力峰值发生在不同介质交界面处。1985年，Nishio[9]通过对不均匀场地下管线的地震响应分析，得到了与Hindy相同的结论。可见，地震作用下埋地管线的破坏主要发生在两种不同介质交界面附近，提高接头变形能力是减小埋地管线地震灾害的有效措施。为此，中外学者开始研究新的具有大变形能力的埋地管线接头，波纹接头因其优越的变形能力得到广泛关注。Yuan等[10]研究了U-、Ω-、C-和S-型波纹接头，其中U形接头工程应用最广泛。Xiang等[11]采用有限元方法，系统研究了钢制波纹接头变形和轴向力学性能，表明波纹接头具有非常优越的变形能力。Lü等[12]开展了波纹接头埋地管线的低周往复荷载试验，表明波纹接头轴向刚度小，能有效地提高管线变形、减小管道轴力。Hamada等[13]对轴向荷载和内压作用下的U形波纹管进行弹性分析，推导出了经验公式；Singace等[14]对波纹管进行实验研究，分析其能量吸收性能，并与PVC管和传统金属管进行对比，表明波纹管具有良好的吸能减能效果。Tsukimori等[15]运用通用非线性有限元分析软件，对内压、外压作用下U形波纹管的屈曲问题进行了研究分析，表明地下管线在不均匀场地下的震害往往比均匀场地下严重，尤其是在软硬土层过渡地带，强震作用下埋地管线将承受较大的轴向变形或弯剪变形。

考虑地下管线穿越软硬两种土层，采用土弹簧模型考虑管土相互作用非线性特征，建立不均匀场地下的埋地直管和波纹接头连接管道有限元模型，数值分析不同地震作用下波纹接头在减小埋地管线应力、能量耗散、管道截面弯矩和管道截面轴力等方面的有效性。

1 有限元模型

1.1 材料模型

管道和接头均选用45号钢，采用双线性随动强化弹塑性本构模型模拟考虑钢材力学性能，材料参数如表1所示。

表1 管道材料特性Table 1 Material properties of the pipes

针对不均匀饱和软土场地下管道的地震响应，选用三、四类黏土进行课题研究，土体材料参数如表2所示。

表2 土体材料参数Table 2 Mechanical properties of soil

1.2 管土相互作用

将管线周围土体简化为一系列的等效弹塑性弹簧，在土弹簧的一端施加地震加速度时程，模拟地震动作用下的管-土相互作用。弹簧力-位移关系如图1所示，因为表层土有临空面，管道向上向下的地基土刚度有明显差异，垂直方向的土弹簧拉压刚度和弹性极限不对称，各方向土弹簧参数的确定参照中国油气输送管道线路工程抗震技术规范计算[16]，计算结果见表3和表4，其中模型一是无接头埋地管线，模型二是采用波纹接头连接的埋地管线。

tu、pu、qu和xu、yu、zu分别表示三个方向的屈服力和土弹簧最大弹性变形值图1 三个方向土弹簧非线性模型Fig.1 Nonlinear soil spring model in three directions

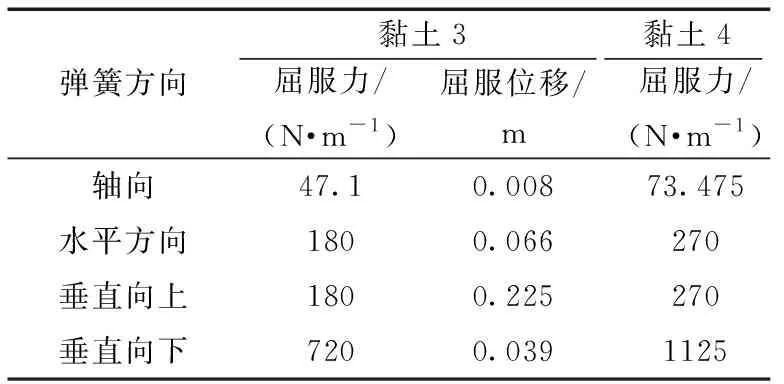
表3 模型一中土弹簧参数Table 3 Parameters of the soil spring model in model 1

表4 模型二中土弹簧参数Table 4 Parameters of the soil spring model in model 2

1.3 单元选取

选用两种介质组合，由于交界面的存在，需要考虑地震动的传播方式，假定能量水平传播，场地简化为有两种介质组成的半无限空间，以垂直平面为交界面，地震能量的传播方向正交于介质交界面。地震波传播方向如图2所示。

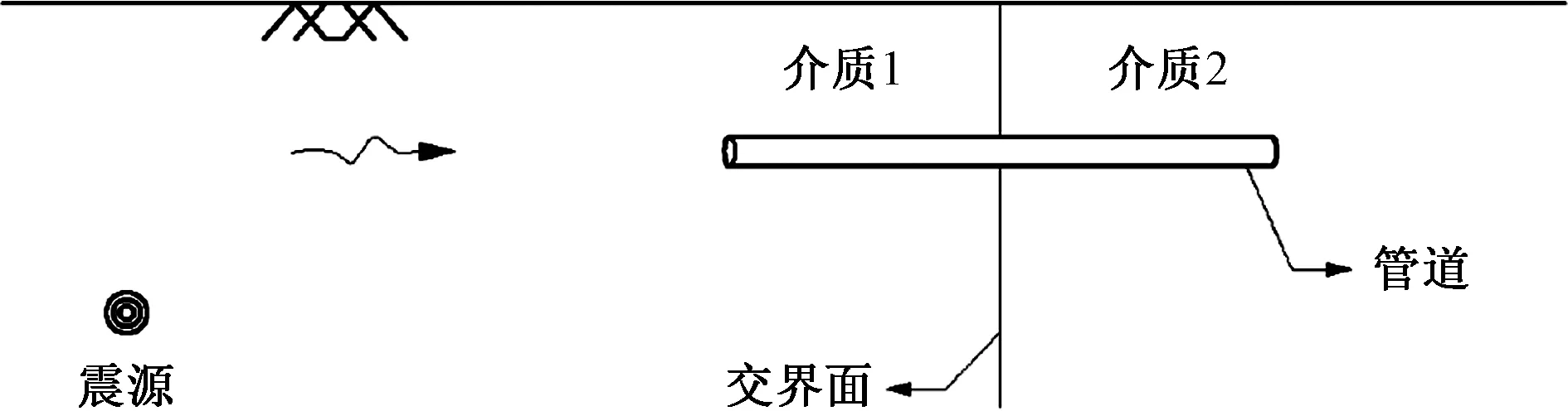
图2 地震传播方向示意图Fig.2 Sketch of the earthquake propagation

钢制管线采用分层壳单元模拟，土-结构相互作用采用弹簧单元模拟并赋予弹簧单元力-位移关系特性。取管线长度为10 m，管径300 mm，管壁厚5 mm，波峰波谷半径13 mm，直线段段长20 mm，网格划分管轴方向设定为50 mm，模型一和模型二的直管部分沿圆周方向划分为20个单元，为了使接头处变形更加均匀，模型二接头处网格进行加密沿圆周划分为84个单元。两种模型节点处分别连接三个方向的土弹簧，约束管线模型两端全部自由度，完成有限元模型模型一、模型二的建立分别如图3所示。

图3 埋地钢制管道有限元模型Fig.3 Finite element model of the pipes

1.4 地震波选取与输入

如表5所示，选取El Centro波、Kobe波和Tianjin波为地震输入，加速度时程曲线如图4所示。将地震动加速度时程峰值加速度调幅为0.1g、0.2g和0.4g(g为重力加速度)，共得到9条加速度时程。沿管线轴向输入地震动时程，约束土弹簧横向、垂直方向所有自由度，将地震动从轴向土弹簧的一端输入，模拟管-土相互作用。假定地震动从软土一侧向较硬土一侧传播，不考虑地震动在两种土层交界面处的折射和反射效应。

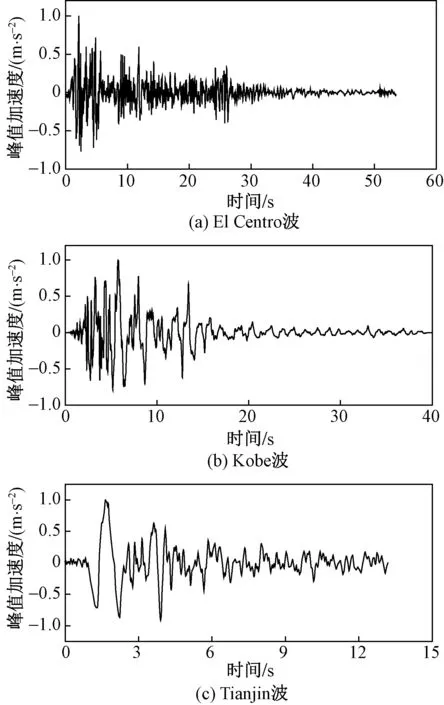
图4 地震波加速度时程曲线Fig.4 Time histories of the earthquake motions

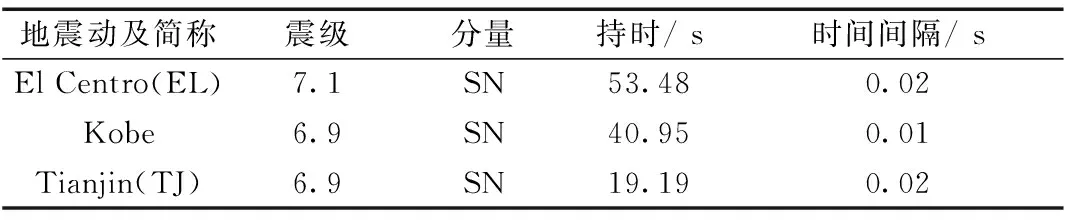
表5 地震波特性Table 5 Characteristics of the earthquake motions

2 分析结果

2.1 能量耗散

为了便于考察波纹管接头对埋地管线的耗能作用，将无接头埋地管线(模型一)与波纹管接头埋地管线(模型二)在九条地震动作用下的最大内能、最大动能做曲线图进行比较，如图5所示。模型二的内能要远远小于模型一，最大减小幅度接近50%；动能在加速度峰值为0.1g时略微有所减小，随着峰值加速度的增加减小幅度逐渐增大，表明波纹管接头可以有效地起到耗能作用，并且在地震响应越大时作用越显著。

图5 不同地震波作用下管道能量耗散Fig.5 Energy of the pipes under different earthquake motions

2.2 von Mises应力对比

以0.2g的El Centro地震动作用下管道von Mises应力为例，模型一和模型二最大应力时刻的von Mises应力云图如图6所示，图中管线变形按照放大50倍显示。模型一中管线最大von Mises应力发生在固端部位，最大von Mises应力为322.1 MPa。管线最大弯曲变形发生在管线中间部位，此处管线的von Mises应力也较大；模型二中，可以看出地震动作用下埋地管线产生的变形主要集中在波纹管接头部位，通过波纹管接头的大变形吸收和耗散地震动能量，管身部位的von Mises应力显著减小，管中最大von Mises应力为291.2 MPa，管身均处于弹性阶段，并且变形小于无接头管线。

图6 El Centro波(0.2g)作用下模型一与模型二von Mises应力云图Fig.6 von Mises contours of the pipes under 0.2g El Centro earthquake motion

为了便于观察接头处变形特性，如图7所示，将接头部位单独取出，位移同样放大50倍以及接头变形历程图如图8所示。可以看出：对于不均匀场地下的埋地接头管道，在El Centro 波(0.2g)作用下，其大变形首先发生在波峰位置，此时接头的变形还处于对称状态；随着时间的增加，变形向波谷转移，波纹管接头向一侧发生弯曲变形，最大von Mises应力出现在波谷位置，其大小为179.1 MPa，远小于接头屈服强度。

图7 El Centro波(0.2g)作用下接头部位von Mises应力云图Fig.7 Contours of the von Mises stress at the joint under 0.2g El Centro earthquake motion

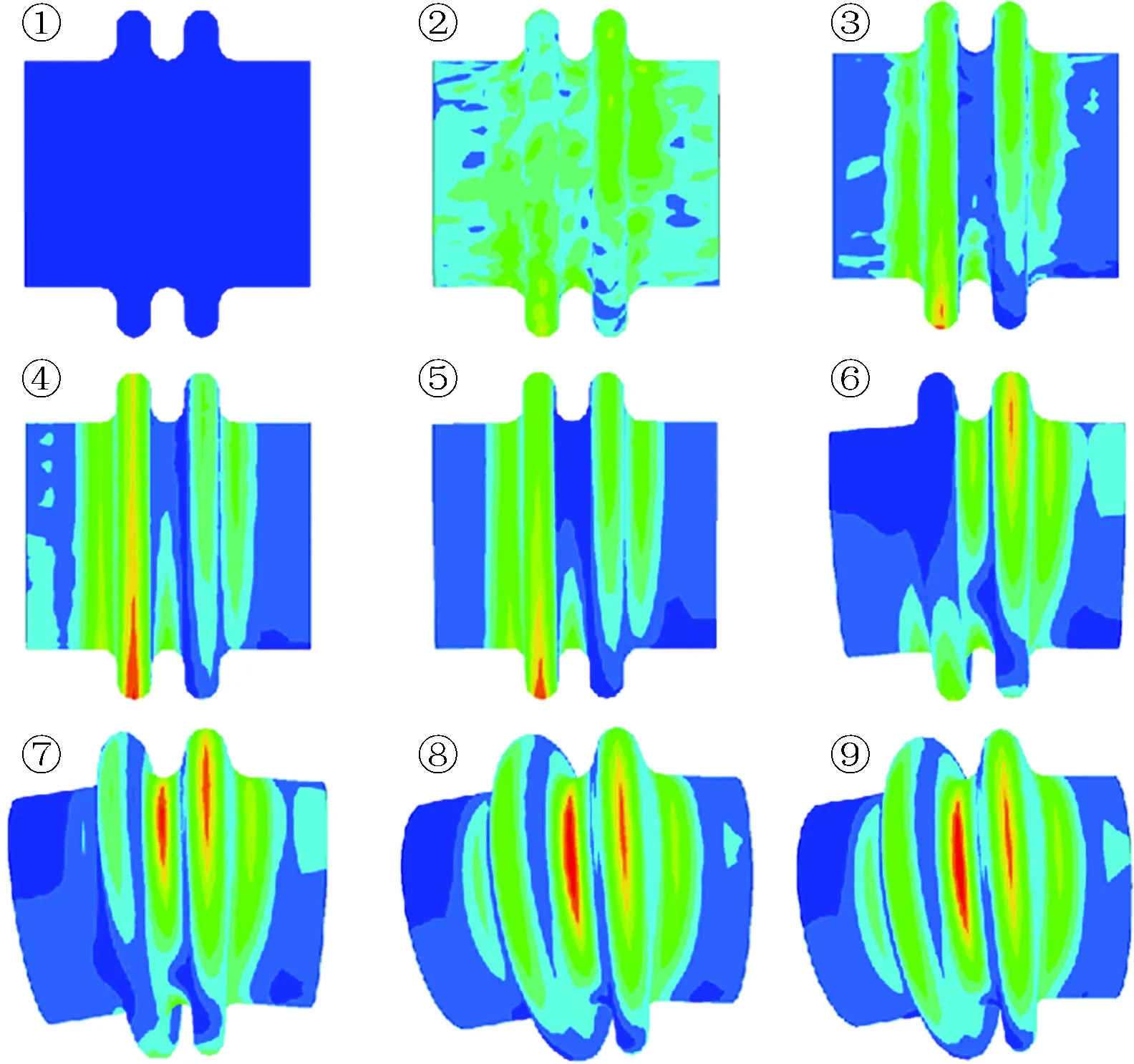
图8 El Centro波(0.2g)作用下接头变形历程图Fig.8 Deformation process of the joint under 0.2g El Centro earthquake motion

分别将两种模型直管部位的最大von Mises应力做曲线图。如图9为各条地震动激励作用下，模型一和模型二分别在介质1、介质2相应位置的最大von Mises应力曲线图。

图9 介质1和介质2中埋地管道最大von Mises应力Fig.9 The maximum von Mises stress of the pipe in clay 1 and clay 2

从图9可以得出，不均匀介质下的两种模型管道在El Centro波、Kobe波、Tianjin波三种地震动作用下均没有达到屈服。在两种介质中的相应位置，模型二直管段部分相对于模型一直管段部分von Mises应力峰值均有所减小，而且软土一侧相对于硬土一侧减小幅度更大，El Centro波、Kobe波、Tianjin波作用下的von Mises应力最大差值分别为104、156、154 MPa。随着峰值加速的增大，减小幅度大致处于同一状态，说明地震动峰值加速度对波纹管接头von Mises应力影响较小。

2.3 管道截面轴力

对两种模型管道沿管轴方向依次取参考截面1～8，截面1～4位于介质2(Clay 3)中，截面5～8位于介质1(Clay 4)中，分别输出相应截面内力做出曲线图。如图10为各条地震动激励作用下，模型一与模型二分别在介质1、介质2相应位置的截面内力曲线图。

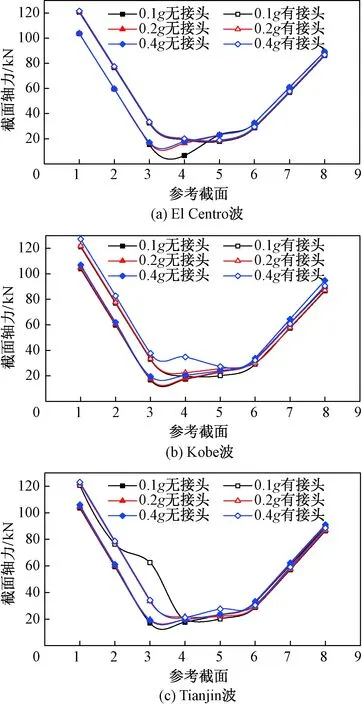
图10 不同地震动作用下模型一与模型二截面轴力Fig.10 Cross-sectional axial forces of model 1 and model 2 under different ground motions

由10可知，不均匀介质下的两种模型管道在El Centro波、Kobe波、Tianjin波3种地震动作用下截面内力变化趋势基本相同。介质2中，模型二截面内力要小于模型一，而介质1中模型二截面内力却大于模型一，这是因为地震动轴向加载方向导致一端受压一端受拉，若同时分析多个接头连接的多个管道，则波纹管接头的控制效果会更明显。另外埋地管线在软硬土不均匀场地下，其地震动加载方向不同，地震响应会有很大不同。

2.4 管道截面弯矩

同样选取参考截面1～8，分别输出模型一与模型二相应截面弯矩做出曲线图。如图11为各条地震动激励作用下，模型一与模型二分别在介质1、介质2相应位置的截面弯矩曲线图。

图11 不同地震动作用下模型一与模型二截面弯矩Fig.11 Section bending moments of model 1 and model 2 under different ground motions

由图11可知，不均匀介质下的两种模型在El Centro波、Kobe波、Tianjin波三种地震动作用下截面弯矩变化趋势基本相同。在两种介质中的相应位置，模型二直管段部分相对于模型一直管段部分截面弯矩均在一定幅度上有所减小，尤其是在波纹管接头附近差值达到最大，El Centro波、Kobe波、Tianjin波作用下的截面弯矩最大差值均在截面4位置，即软土一侧接头附近，分别为33.09、31.7、33.9 kN·m；减小率均在50%左右，响应最大减小率分别为85.44%、82.7%、82.55%。证明波纹管接头能有效减小管道弯矩响应。而且软土一侧相对于硬土一侧减小幅度更大，随着峰值加速的增大，减小幅度大致处于同一状态，说明波纹管接头在减小截面弯矩方面不随震级的变化而大幅度波动。

3 结论

对管道失效准则进行介绍，在此基础上对不均匀场地下埋地管线进行地震响应分析。首先采用三种地震动(El Centro波、Kobe波、Tianjin波)分别调整峰值加速度调幅为0.1g、0.2g、0.4g，从von Mises应力、管道应力、管道应变、截面内力以及截面弯矩几个方面对不均匀场地下无接头埋地管线进行地震响应分析，得到如下结论。

(1)地震动作用下不均匀场地埋地管线最大von Mises应力在交界面附近异常增大，其峰值随着地震烈度的增大而小幅增大；管线位于软土一侧的地震响应要大于其位于硬土一侧。

(2)地震烈度对不均匀场地下埋地管线的von Mises应力峰值大小虽然有一定的影响，但是影响不太大。

(3)波纹接头可以有效减小管中内能和动能、von Mises应力、截面弯矩、截面轴力，减小幅度随着峰值加速度的增加而增大。

(4)不均匀介质下，接头的变形是轴向拉伸和弯曲变形的耦合，波纹管接头对减小交界面附近以及软土一侧耗能效果更加显著，地震动峰值加速度对von Mises应力的减小效果影响不明显。

(5)地震动作用下埋地管线变形主要集中在波纹管接头部位，管线峰值应力主要出现的波纹接头波峰和波谷位置。