纳米通道内石墨烯基传热的非平衡分子动力学研究

赵津 秦杨军 刘畅 刘照 张航

(1.贵州大学 现代制造技术教育部重点实验室，贵州 贵阳 550025；2.贵州大学 机械工程学院,贵州 贵阳 550025)

随着电子技术的迅速发展，电子器件的集成化程度不断提高的同时，电子器件的尺寸越来越小，功率密度和热量的产生越来越大，对电子元器件的散热提出了更高的要求，研究微观纳米尺度下的传热特性及其机理显得十分重要。分子动力学(MD)模拟被作为一个探测微纳尺度的有效手段，被广泛应用在微纳尺度的科学研究中。

界面热阻作为衡量热量传递的关键物理量。在多固体界面的接触过程中会产生接触间隙，接触间隙中介质的导热性质影响着热量的传递。石墨烯具有大的比表面积[1]和优良导热性，其中石墨烯层面内热导率高达5 300 W/(m·K)[2]，常被用来作为基底材料,硅基体和单层石墨烯的界面热导高达450 MW/(m2·K)，随着层数的增多界面热导降低[3]。Shahil等[4]使用单层和多层石墨烯作为填料可使热导率最高提升2 300%。但是固液界面热阻却不相同，由于固液界面不存在接触间隙，固液相互作用强度[5- 8]、固体结构[9]、表面粗糙度[10]、壁面温度[11- 12]、热震荡频率[13]等成为了主要的影响因素。梅涛等[14]利用分子动力学的方法研究了在不同壁面温度和壁面湿润性的条件下，界面热阻的变化规律，发现壁面润湿性的增强会显著降低界面热阻。Soong等[15]研究了固体晶格平面等因素对流动传热的影响机制，结果发现固体结构对速度滑移和温度阶跃有明显的影响。张程宾等[16]利用分子动力学的方法分析了粗糙表面对纳米尺度流体流动和传热与温度阶跃的影响，结果表明粗糙度的存在使得纳米流体产生了额外的黏性耗散，使通道内速度水平小于光滑通道,温度水平高于光滑通道,并且粗糙表面的速度滑移与温度阶跃均小于光滑通道。Barisik等[17]利用分子动力学方法分析了纳米通道中壁面温度对界面热阻的影响,发现壁面温度越高,界面热阻值越大。

界面热阻由载热子的散射程度决定，声子成为了主要的热载流子[18]。张龙艳等[19]采用非平衡分子动力学方法分析了尺寸效应对固液界面热阻及温度阶跃的影响，结果表明界面热阻随着小尺寸微通道递增而递增，大尺寸微通道中固液原子声子失配程度近似不变,使得大尺寸微通道的界面热阻呈恒定值阶段。上述研究都是从固液内部结构作用分析其传热机理，鲜有将石墨烯层作为传热层来研究其对固液传热的相关影响，对现在广泛使用的半导体材料在固液界面间传热及其应用上的研究略有欠缺。由于流体氩原子之间的相互作用力简单，便于进行模拟与计算。文中主要研究单层石墨烯[20]作为铜壁面与Ar流体之间导热层的传热规律；不同壁面温度对固液界面温度阶跃的影响，并从声子态密度层面分析引起界面热阻变化的原因；探究单层石墨烯在流动状态与不同壁面温度下，对流体速度滑移和温度阶跃的影响。

1 物理模型及模拟细节

文中模拟体系如图1所示,x，y，z方向分别为1.21，5.2和15 nm。上、下壁面各有7层铜原子，中间为氩流体区域，固体区域与流体区域之间上、下各有一层石墨烯，与铜[1 0 0]晶面配合，靠近石墨烯层部分为热沉和热源，与流体区域进行热量的交换。x、y方向均设置为周期性边界，z方向为固定边界条件，固体壁面铜原子按照面心立方(FCC)晶格排列，对应的晶格常数为0.312 5 nm，流体区域氩原子也按照FCC晶格排列方式布置，对应晶格常数为0.585 nm，共有9 826个液体原子，单层石墨烯共有4 592个碳原子，石墨烯原子之间以C—C键相互连接。

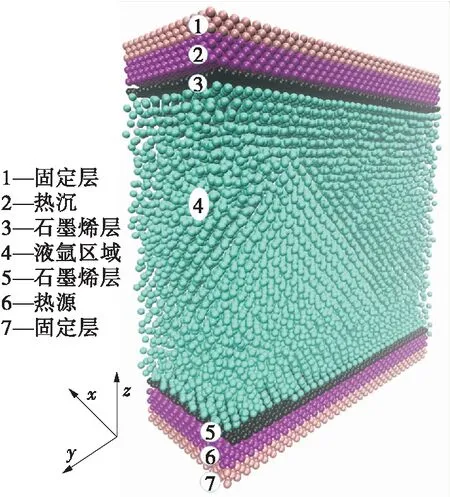
图1 物理模型结构示意图

牛顿运动方程是分子模拟的基础，通过求解系统中所有粒子的运动方程，最终得到各个时刻粒子的速度、力和位置坐标等；通过统计理论，得到温度和压力等各种宏观信息。势函数用来描述原子、分子间的相互作用。石墨烯中的碳原子相互作用选用AIREBO[21]势函数,能更好的描述碳原子间的相互关系。在金属原子之间，EAM势函数可以很好地描述其相互作用，表示为

(1)

式中，Ei为每个原子i的总能量，Fα为迁入能，rij为原子之间距离，ρβ为电子云密度，φαβ为原子间的势能。而在单原子氩和金属原子铜和石墨烯，以及氩原子之间的相互作用势最常用的为Lennard-Jones势函数，表示为

(2)

式中，uij为非键结合势能，ε为流体粒子和固壁粒子之间的作用势能量,δ为流体粒子和固壁粒子之间的距离参数。其中氩原子间能量参数ε=0.010 4 eV，δ=0.340 5 nm[22]，铜、氩以及碳原子之间的势能参数参考文献[23]，在模拟过程中势能的截断半径取1 nm，原子间距离超过截断半径，则相互作用力忽略不计。

在本文的分子模拟中，求解牛顿运动方程采用的是Velocity-Verlet算法，时间步长为1 fs，在模拟前利用共轭梯度法，减少模拟体系达到平衡态所需要的时间。在初始时刻利用高斯随机分布给各个原子赋予初始速度，在NVT系综下对整个体系进行恒温处理，并且运行1 ns使得各个部分的温度稳定在80 K。随后撤掉系统整体温度热浴，热源部分的升温采用Langevin方法升至额定温度，其余部分采用微正则系综，热源与热沉的温度差为Δt，运行2 ns进行数据的统计和采样。对比无石墨烯传热层对温度阶跃和界面热阻的影响，并从声子态密度角度分析原因，最后在流动状态下分析了石墨烯层对流体速度滑移和温度阶跃的影响。

2 结果与分析

2.1 液态氩热导率的验证

为验证文中MD模拟的准确性，以及进行更深一步的研究，本节采用非平衡方法对氩流体的热导率进行计算验证。Fourier定律为

(3)

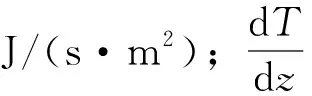
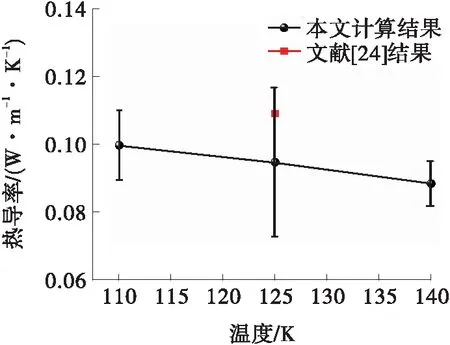
图2 液态氩的热导率验证

2.2 温度阶跃与密度分布

本节主要讨论的是石墨烯传热层对铜壁面与流体Ar之间温度阶跃和密度分布的影响，由于微通道内流体原子的分布状态会影响固液间能量的传递，研究石墨烯层在不同固液温差下流体密度的分布和温度分布显得十分有必要。在此次MD模拟中分别取热源温度Thot=140,125,110 K。为了观察并统计出流体区域内的温度和密度分布，在z方向将整个体系平均划分为40层，对每层原子的温度求平均，得出整个模拟体系在z方向上的温度分布；将流体区域沿着z方向平均划分成500层，得出每层流体区域的密度。

图3为纳米通道中流体区域的温度分布情况，由于界面热阻的存在，由图3可以明显看到温度阶跃现象，在无石墨烯传热层的Ar/Cu纳米通道中，热源温度升高均会导致热源与流体，热沉与流体两个界面温差升高，热源温度Thot为140 K时，最大温差为16.8 K，温度的升高会增加固体壁面流体原子的动能，使得固液间原子的碰撞加剧，能量传递增强，这也解释了热源处固液界面温差小于热沉处固液界面温差的现象。而固液间存在石墨烯传热层时，均会不同程度降低固液界面温差，其中最大温差为8.7 K，降低幅度可达48%，石墨烯层无疑会增强固液壁面间能量的传递。

图3 纳米通道中流体温度分布

图4为纳米通道中流体密度分布，在近壁面处的流体密度振幅较大，这是由于固体原子与流体原子之间存有相互作用，会在近固体壁面的位置存有一层或多层排列规则的液体，当温度为100 K时,晶体氩的密度为1.48 g/cm3,发现近壁面处的氩原子密度远高于结晶密度，近壁区的氩液体原子结构也被称之为类固体结构。相关研究表明，固液间作用力是影响类固体结构层数的重要因素，固液间作用力增大，该结构的层数就越多，界面热阻也就越小，传热性越好。当增加热源温度，流体区域的温度也会随之增加，近壁面处流体原子动能增加，使其逃逸壁面原子束缚的能力增强，使得近壁面处流体密度振幅逐渐降低，而这也解释了热源和热沉近壁面处类固体层数不一的原因。图5对比了有无石墨烯传热层密度的分布趋势，流体原子与石墨烯之间的作用力小于与固体壁面间的作用力，石墨烯层的存在反而增加了近壁面处的流体密度，主要是因为石墨烯层具有较大的比表面积。

石墨烯层具有较大比表面积的特点，是热量传递的一种高效介质。固液能量传递的过程也通常被认为是载热子的传递过程，加上类固体结构的存在，可以减少载热子的界面散射程度，从而增强传热，降低界面热阻。又因为石墨烯为单层结构，对热载子的散射影响较小，综上所述单层石墨烯可以降低固液界面温度阶跃，增加近壁面处流体的密度分布，增强固液界面间的热量传递。

2.3 界面热阻与声子态密度分析

在微尺度下，界面热阻效应尤为明显，其为两界面间温度差与通过该界面的热流密度的比值：

(4)

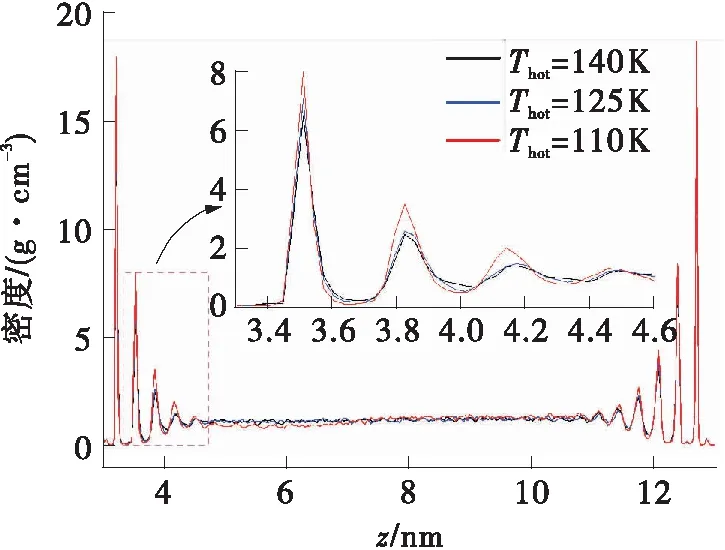
图4 纳米通道中不同热源温度下的密度分布

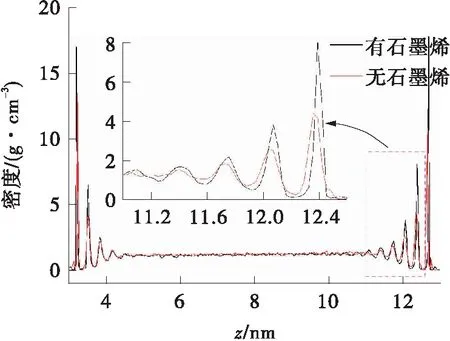
图5 纳米通道中的密度分布

图6 不同热浴温度下的界面热阻

无石墨烯传热层时，热源温度从110 K到140 K，热界面热阻从6.47×10-8m2K/W降到4.73×10-8m2K/W，降幅达26.9%。在固液界面间加入单层石墨烯，热源温度分别为110、125和140 K时，热源界面热阻值降幅分别为38%、45.9%、42%，热沉界面热阻值降幅分别为8%、35.6%、28.6%。在图6中，对于相同体系而言，壁面温差越大，热源界面处界面热阻低于热沉界面处界面热阻的效果越明显；相反，壁面温差越小，热流与温度梯度变化不明显，效果越弱。有石墨烯传热层的体系中，热源界面和热沉界面处的界面热阻均低于无石墨烯层的体系。石墨烯层的存在降低了界面热阻值，增强了固液界面间的热量传递。

固液界面间的热量传递也常被认为是热载子的传递过程，在声子理论中界面热阻是由相邻两种原子的振动态密度失配程度决定的，原子间的声子振动态密度(VDOS)ρVDOS失配程度越低，界面热阻越小[19]。文中VDOS是将速度自相关函数(VACF)进行傅里叶变换得到：

(5)

式中,v为原子速度，〈〉为统计平均，w为原子的振动频率。固液原子间振动态密度的失配程度影响着固液间的传热，失配程度为

ΔρVDOS=|ρVDOS1-ρVDOS2|

(6)

图7中为热源、氩流体和石墨烯的声子振动态密度。在本次MD模拟中，利用热源、热沉和近壁面处(1 nm内)的流体域原子计算振动态密度。图7中壁面金属的振动态密度值分布在高频部分，流体部分的振动态密度分布在低频部分，这主要是因为固体原子之间的作用力强于液态原子之间的作用力。图中很明显可以看到，液氩和石墨烯间的振动态密度失配度低于金属壁面和液氩之间的失配度，这也就解释了在固液之间加入单层石墨烯会导致界面热阻降低、固液间热量传递加强的现象。

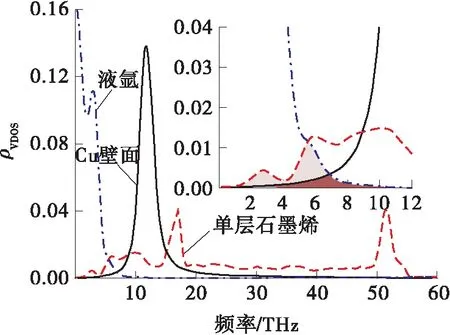
图7 热浴温度为140 K时固液原子VDOS分布

综上所述，固液间的热量传递很大一部分是由热载子的散射程度决定，原子间的VDOS失配程度越低，界面热阻越小。梅涛等[14]通过改变固液势能强度来研究壁面润湿性对传热的影响，固液势能作用强度越大，壁面润湿性越好，固液间温度阶跃越小，固液界面热阻越小。本文在固液界面处采用单层石墨烯作为传热层，石墨烯与氩流体的势能强度低于铜壁面与氩流体的势能强度，石墨烯表面的润湿程度低于金属壁面的润湿程度，传热效果反而得到了提升，高达46%，因此，石墨烯传热层降低界面热阻，提高传热效果的原因，可以归结于石墨烯独特的单层结构。

2.4 流动状态下的速度滑移和温度阶跃

本小节主要研究在流动状态下液氩速度和温度的分布情况，整个体系在NVT系综下运行1 ns，整个体系达到指定的80 K温度后，取消恒温系综，流体区域采用NVE系综，并对所有流体原子施加额外的作用力F=1.6×10-12N，热源部分的温度用NVT控温，取140、125和110 K，热沉恒温于80 K。在此条件下分别运行1 ns，取后0.1 ns的数据值进行分析。

图8为纳米通道内的速度分布，存有石墨烯的体系中固液界面处出现明显的速度滑移，滑移速度为40 m/s。由于固液原子间相互作用力的存在，导致近壁面处的流体受到黏性力的作用，相互作用越弱，滑移程度越大，流体的黏性耗散越小，纳米通道中的流动速度越大,相比于无石墨烯的体系，纳米通道中心速度增幅达24%；但是在无石墨烯的体系中却出现负滑移，滑移速度达45 m/s。壁面原子与液氩之间的作用力强于石墨烯与液氩之间，导致近壁面处的流体分子受到较大的黏性力，导致固液间的速度滑移程度减小，当流固作用强度大于一定程度时，随着密度的增大会出现负滑移现象，这与Priezjev[25]研究边界滑移所得出的结论吻合。从图中可以看出，壁面温度对纳米通道内速度分布的影响程度较弱。综上所述，石墨烯传热层的存在，提升了纳米通道内的流体流速，可以较大程度的增加速度滑移程度，这也合理解释了Hummer等[26]发现碳纳米管中流体流量增加数倍的原因。

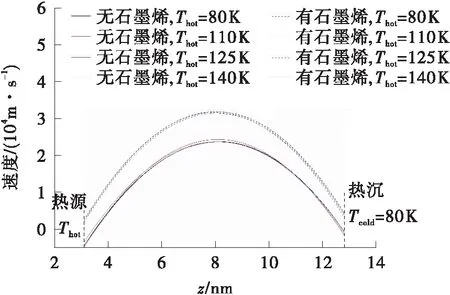
图8 纳米通道中流体的速度分布

固液原子间作用力的存在不仅会影响流体的速度分布，同时也会影响流体温度的分布。热源的温度Thot分别取140、125、110和80 K，热沉的温度始终为80 K。流体原子在力的作用下，其运动包含流体分子间的热运动和宏观运动，减去流体区域的宏观运动后纳米通道中流体热运动的温度分布如图9所示。在有无石墨烯的体系中，升高壁面温度，纳米通道内流体分子间的热运动程度均会增加，导致流体温度升高。在无石墨烯传热层的体系中，热源温度Thot从80 K升高到140 K,壁面处的温升达30 K，同道中心处的温度最大为333.6 K，且纳米通道中温度最高位置向热源壁面偏移；在有石墨烯传热层的体系中，近壁面的温度相比无石墨烯的体系，最高涨幅可达5 K,主要是因为石墨烯具有较大比表面积，导致近壁面处流体密度增加，分子之间的热运动程度增加导致，而纳米通道最高温度与无石墨烯传热层相比，降幅最大为10 K。综上所述，石墨烯传热层的应用可以增大纳米通道内的流速，增大壁面处的速度滑移，同时也可以减少流体内摩擦的损耗，使得温度不进一步的升高。

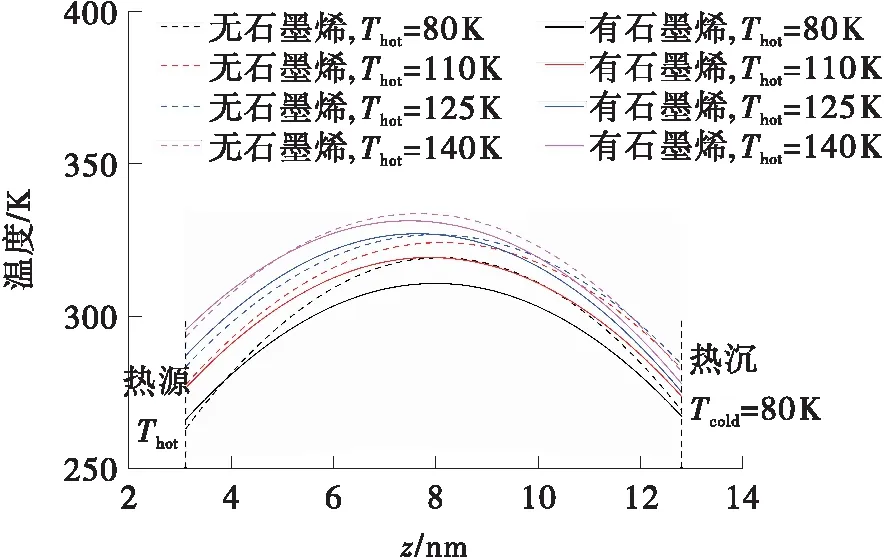
图9 纳米通道中的温度分布

3 结论

文中利用非平衡MD方法对纳米通道内石墨烯层传热的相关特性进行研究，对比分析了不同温度下，单层石墨烯对纳米通道内固液界面的温度阶跃和流体密度分布的影响；以及定量研究了界面热阻的变化趋势，并从声子态密度的角度阐述内部机理；随后通过添加外部驱动力，使流体处于流动状态，研究流动状态下的速度滑移和温度阶跃。发现石墨烯对于提高界面传热效率和增加纳米通道内流速效果明显，并得到如下结论：

1)石墨烯层可降低界面温度阶跃增强传热，与无石墨烯传热层纳米通道相比，温度阶跃降低幅度最大可达48%，石墨烯具有较大的比表面积，从而使近壁面处的流体密度增大，增强了界面间的传热。

2)石墨烯层可降低固液界面热阻值，热源界面、热沉界面热阻降幅最大分别为45.9%、35.6%。固液界面热阻值主要由低频部分VDOS的失配程度决定，石墨烯与液态原子之间的失配程度低，热量传递效果好。

3)在流动状态下，石墨烯层可增加近壁面处流体的滑移程度和通道内流体的速度，减小流体所受剪切力程度，同时也会增加近壁面处的温度阶跃，降低通道内的最大温度。