制动工况下液力变矩器大涡模拟流场仿真及可视化试验验证
2022-04-29柴博森王广义朱国仁闫东陆振华迟成芳
柴博森 王广义 朱国仁† 闫东 陆振华 迟成芳
(1.吉林大学 机械与航空航天工程学院,吉林 长春 130022; 2.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022; 3.长安大学 高速公路筑养装备与技术教育部工程研究中心,陕西 西安 710061; 4.江苏华隆兴机械工程有限公司,江苏 无锡 214023)
液力变矩器(TC)是自动变速汽车和工程机械领域广泛应用的关键基础部件[1]。目前高性能液力变矩器产品严重依赖国外进口,核心研发技术掌握在德国采埃孚(ZF)和日本爱信(Aisin)等国际知名企业中。液力变矩器先进设计理论与关键技术的缺失已成为制约我国自动变速汽车和工程机械领域发展的“卡脖子”问题,只有加强对液力变矩器基础理论的研究和前瞻性技术的突破,才能满足国家在自动变速汽车和工程机械领域发展的战略需求,为国民经济支柱产业汽车工业和工程机械的蓬勃发展强筋健骨。
液力变矩器是依靠流体传动实现能量转换的叶轮机械,其内部流动特性决定外部工作性能,深入研究其内部湍流时空演化规律与流动控制机理对于优化设计其叶栅结构及性能改进具有重要的科学研究意义[2]。目前研究液力变矩器流场的主要手段是基于计算流体动力学(CFD)的数值模拟方法和采用非接触测量方式的流场可视化技术[3]。在数值模拟方面,人们已经深刻地体会到发展高精度数值模拟方法对于精细刻画湍流时空演化特征并准确地预测工作特性的重要性[4]。基于大涡模拟(LES)方法开展液力变矩器湍流高精度数值模拟已成为一项极具挑战性的科研课题。国外,Odier等[5]提出了一种适用于复杂壁面模型大涡模拟的网格自适应方法,综合考虑壁面边界层y+值和平均动能耗散,预测了涡轮内部湍流特性。Yang等[6]提出一种新型的壁面建模方法,采用大涡模拟预测近壁面流场分布情况。日本北海道大学Tasaka等[7]采用大涡模拟仿真液力变矩器内部的三维流动,并进行了流场试验对比分析。Fuente等[8]采用k-ε湍流模型仿真了液力变矩器在瞬态和稳态时的流场特性,但该两方程湍流模型仿真精度不足。国内,同济大学王立军等[9]基于大涡模拟技术,采用格子Boltzmann方法数值模拟了液力变矩器导轮流场,重现了导轮叶片尾迹区复杂的流动细节。北京理工大学刘城等[10]基于大涡模拟应力混合涡模型仿真了高功率密度液力变矩器内流场,揭示了流场能量损失机理。哈尔滨工业大学杜明杰采用大涡模拟方法仿真了涡轮内部流场,分析了叶片表面凹坑结构对壁面边界层流场的影响规律[11]。在流动可视化试验测量方面,激光多普勒测速(LDV)和粒子图像测速(PIV)逐渐成为液力变矩器湍流实验测量研究的主流技术。国外,美国亚拉马巴州大学Lee等[12]基于LDV技术揭示了液力变矩器内部流动特性,研究了泵轮、涡轮之间转速差对其内部复杂流动效应的影响规律。弗吉尼亚大学Flack等[13]采用激光测速技术测量了液力变矩器涡轮和导轮内部流场并分析了不同转速比下流速的变化。韩国机械技术学会Yoo等[14]基于LDV技术对泵轮和涡轮叶片之间的流场区域进行测量,发现涡轮的瞬时位置对叶轮通道间隙区域内的流体流动有较大影响,且单点测量具有一定的局限性。日本福井大学Yamamoto等[15]基于PIV技术实现了液力变矩器流场可视化,提出了二进制图像互相关算法进行流场计算。国内,北京理工大学祝自来等[16]基于LDV技术测量了液力变矩器流场,详细分析了示踪粒子直径、浓度对其跟随性的影响规律。北京理工大学李晋等[17]利用LDV技术测量了液力变矩器泵轮流场,发现导轮对泵轮流道上游的影响强于涡轮,而涡轮主要影响泵轮出口处的低流速区域。吉林大学柴博森等[18]基于PIV技术采集了液力变矩器涡轮流场图像,发现提高转速比后,二次流、反向流等复杂流动现象逐渐降低,流动能量损耗降低。吉林大学柴博森等[19]基于二维切面流场试验测量系统采集了制动工况下液力偶合器径向切面漩涡流场图像,经图像后处理识别剔除错误流速矢量,优化了流动图谱。综上所述,近些年研究者越来越关注液力变矩器内部流场数值模拟与试验测量,但是在流场高精度仿真与流动可视化精确测量等方面仍然存在很多亟待解决的科学问题。尤其是针对大涡模拟流场仿真,在湍流模型的合理选择及其计算方法的正确应用等方面需要开展更深入的研究。
为了准确地揭示液力变矩器流场时空演化机理,基于大涡模拟技术采用5种亚格子湍流模型精细化仿真液力变矩器流场,对比分析流场仿真结果的差异性。通过PIV流场可视化试验验证数值模拟结果的可靠性,并对5种亚格子湍流模型的仿真适用性进行分析。
1 研究对象
1.1 计算模型
建立液力变矩器三维模型,其循环圆有效直径为315 mm,泵轮叶片数28个,涡轮叶片数27个,导轮叶片数17个,如图1(a)所示。为了简化计算域,忽略各叶轮间的流体泄露,认为液力变矩器3个叶轮组成了封闭的耦合流动域,经过布尔运算提取全流道几何模型作为流场计算域,如图1(b)所示。

图1 液力变矩器计算模型
1.2 网格模型
基于ICEM软件采用六面体结构化网格对液力变矩器全流道计算模型进行精细化网格划分。由于叶片近壁面边界层流动情况对整体流道内部流场演化过程影响显著,为了精确化求解叶片近壁面流场结构,对叶片近壁面区域进行局部网格加密处理,如图2所示。考虑网格无关性因素[20],调整最终确定全流道计算域总体网格数为3427543。

图2 全流道网格及叶片近壁面网格加密处理
2 数值计算方法
2.1 控制方程
采用大涡模拟(LES)方法数值计算液力变矩器流场。LES的控制方程是滤波函数对N-S方程进行滤波得到,基于网格尺寸筛选,比网格尺寸小的涡被忽略,大涡直接解析,小涡被模化,滤波函数计算公式如下:
G(|x-x′|)=
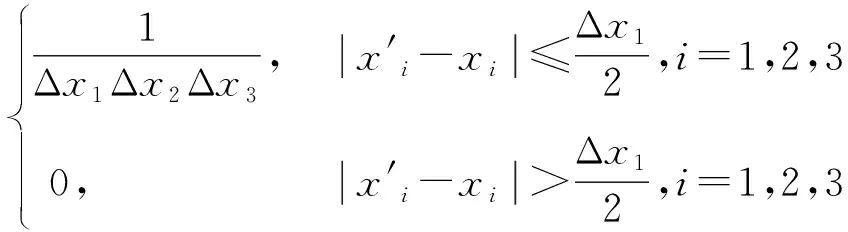
(1)
式中,G为滤波函数,xi为张量形式的指标,Δxi为坐标系中沿i方向上的网格尺度。
经过滤波的大涡模拟控制方程如下:
(2)
式中,ρ为流体密度,t为时间,ui和uj为张量形式的时均速度,xj为张量形式的指标符号,p为压强,μ为流体黏度,带有上划线的量为滤波后的场变量,ij表示滤波后得到的大小尺度脉动之间动量交换的亚格子应力项,可通过下式求解:
(3)
式中,Sij为应力张量比率,kk为各向同性的亚格子应力,μt为亚格子尺度的湍流黏度。
2.2 亚格子模型
亚格子湍流涡黏度μt定义不同则构成不同亚格子模型,文中采用涡黏性模型(SL)、局部涡黏度壁面自适应模型(WALE)、代数形式的壁面函数模型(WMLES)、改进的代数形式的壁面函数模型(WMLES S-Omega)和动态动能亚格子模型(KET)5种亚格子模型来数值模拟液力变矩器流场。
SL模型[21]满足控制方程如下:
(4)
亚格子涡黏度由下式定义:
(5)
式中:δij为克罗内克函数,Smagorinsky系数Cs常取0.1;网格尺寸V决定滤波尺寸Δ,Δ=V1/3。
WALE模型[22]湍流涡黏度表达如下:
(6)

(7)

WMLES模型[23]是为了克服雷诺数的尺度限制而提出的,湍流涡黏度μt定义为
μt=(CSmagΔ)2S{1-exp[-(y+/25)3]}
(8)
式中,S为应变率,常数CSmag=0.2,y+为第一层网格质心到壁面的无量纲距离。
由于WMLES模型没有考虑恒定剪切流中的零涡黏性,WMLES S-Omega模型被提出来解决恒定剪切流中的零涡黏性现象建模,在这个模型中只是将式(8)中的S替换成|S-Ω|,其中Ω为旋涡强度。
KET模型考虑了亚格子尺度湍动能的模拟,湍流涡黏度μt可通过以下方程组求得:
式中,Ck为模型系数,ksgs为湍动能,qsgs为亚格子湍动能。
2.3 计算方法
以纯净水作为液力变矩器工作介质,密度ρ=998.2 kg/m3,黏度μ=0.001 003 Pa·s,忽略流动介质温度变化对密度和粘度的影响及流动泄漏的影响,设置各叶轮交界面为滑移网格,壁面处采用无滑移边界条件。基于ANSYS-Fluent软件采用大涡模拟亚格子湍流模型仿真制动工况(i=0)下液力变矩器流场,i为传动比。泵轮输入转速为200 r/min,计算方法选取SIMPLE算法,压力方程使用Standard格式离散,采用二阶迎风格式求解动量方程与湍动能,设置瞬态求解时间步长0.01 s,迭代计算总步数为500,监测残差曲线与泵轮转矩曲线作为判断仿真结果是否收敛的依据。
3 流场仿真结果
3.1 三维涡识别与流场结构分析
流体力学科学家柯奇曼(Kucheman)认为旋涡是流体运动的肌腱[24]。液力变矩器工作时其内部充满紊乱且不同尺度下的旋涡流动,多尺度旋涡流动的产生、发展以及彼此之间的相互作用支配着液力变矩器内部整体流动。准确地识别并提取液力变矩器三维涡旋结构特征,对于揭示其内部湍流时空演化规律及流动能量转化与损耗机理具有重要的推动作用。在流场数值模拟的基础上,利用CFD-Post软件对流场仿真结果进行后处理,基于Q准则涡识别方法,选取合理阈值识别并提取液力变矩器内部整体三维涡旋结构,如图3所示,其中涡轮叶片、泵轮叶片、导轮叶片分别采用红色、白色和黑色区别表示,紫色箭头表示从泵轮到涡轮的流动方向,黄色箭头表示涡轮与导轮之间的流动趋势。
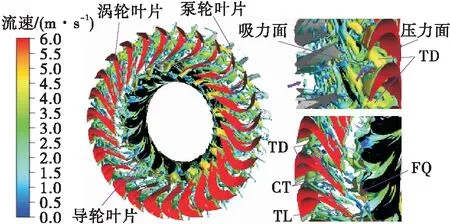
图3 三维涡时空结构
制动工况下,涡轮静止不动,携能高速流体由泵轮流道流出,冲击涡轮叶片压力面,由于涡轮叶片几何扭曲程度大,导致沿叶片壁面处流体速度大小和方向急剧改变,形成多尺度涡旋结构,并由此驱动引起涡轮流道内部形成丰富多彩的不同结构的多尺度涡旋结构,如:通道涡(TD)、长条涡(CT)、发卡涡(FQ)、脱落涡(TL)等,如图3所示。在离心力和叶片的双重作用下,泵轮流道入口处小尺度分离涡经过旋转、合并后逐渐形成较大尺度的混合涡结构,并加速冲击进入涡轮流道内。由于涡轮叶片空间扭曲程度大,在扭曲叶片的作用下,逐渐在涡轮主流区域上形成明显的通道涡,在这个过程中伴随着多尺度涡结构的汇聚与合并,不断强化通道涡结构的强度,并集聚大量能量,促成主流区域上的大尺度旋涡流动,考虑流体粘滞损耗,一部分流动动能转化为流体内能,并最终以热能形式耗散。随着主流区域旋涡能量逐步向涡轮流道出口处传递,由于出口处流道空间变狭窄,流道出口处横截面积变小,导致涡轮出口处流动加速,通道涡在拉伸、弯曲、扭转、撕裂的作用下,逐渐由较大尺度涡旋结构转变为小尺度下的长条涡结构,如图3涡轮出口处再次形成长条涡,且该处长条涡结构左侧多呈现粗圆状,右侧多呈现尖细状,整体结构形态类似于“子弹”形式,呈现加速状态。在涡轮与导轮交界面无叶栅区域,出现部分小尺度脱落涡结构,伴随一定的能量损耗。涡轮出口处的流体经过空间扭曲叶片的扬抛作用,以较大的入射角冲击导轮叶片头部,在导轮入口处靠近叶片吸力面位置形成发卡涡,并紧贴着叶片吸力面逐渐向后蔓延。为了揭示制动工况下涡轮流道内部非定常多尺度涡时空演化规律,基于Q准则涡识别方法精细提取5种亚格子湍流模型仿真结果中的多尺度涡旋结构,选取阈值55 842.1 s-2,提取结果如图4所示。

图4 五种湍流模型涡轮流道三维涡结构
图4展示了5种亚格子模型涡轮流道瞬时三维涡空间分布形态。WMLES和WMLES S-Omega模型在叶片吸力面附近涡分布较密,流场情况更为复杂,而SL模型在该区域内涡结构识别不够准确,没有捕捉到较为详细的流场状态。主流区域上,WALE模型在该区域内涡结构破碎,这是由于携能大尺度涡转化为小尺度涡过程中,中间伴随着涡的拉伸、撕裂、碰撞、合并等动力学作用,引起流场结构剧烈变化,引起能量传递损耗。SL模型没有模拟出叶片压力面处的小尺度涡旋结构,而其他模型均有体现。由于考虑亚格子尺度湍动能数值模拟,KET亚格子模型针对叶片尾部的脱落涡结构仿真结果相对于其他模型更加逼真。
3.2 瞬时流速场和涡量场分析
通过PIV试验验证仿真结果的准确性。截取数值模拟后的流速场和涡量场,如图5所示,所截取的截面与PIV试验测量中的二维截面保持一致。
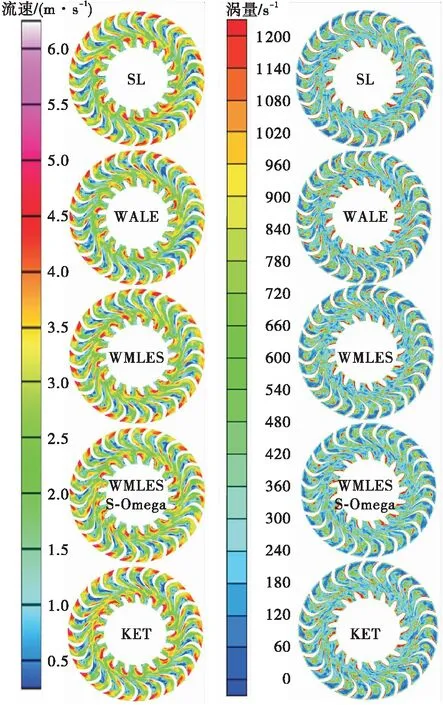
(a)流速 (b)涡量
从流速场整体结构分布来看,5种亚格子湍流模型仿真结果周期性明显,如图5所示。从流速场局部分布定性来看,在涡轮流道入口处,外环与叶片吸力面的角隅区域存在明显的高速区,这是由于来自泵轮流道内部的高速液流冲击进入涡轮流道,经扭曲涡轮叶片的扬抛作用,进而加速流体运动而引起流速增大的结果。低速区主要集中在流道中间位置靠近吸力面处,这是由于液流冲击涡轮压力面导致流速大小和方向发生骤变,进而形成多尺度旋涡结构,且这些多尺度旋涡结构彼此之间发生冲击、合并、分离相互作用,引起流动能量转变和损耗。由于液流粘滞损耗的作用,部分损失的流体能量导致流体介质温升,流体动能转化为内能并最终以热能形式耗散。在涡轮出口处由于流道变狭小,流速逐渐升高。
从涡量场整体分布来看,高涡量场主要集中在涡轮中间位置高、低流速交界处和近壁面区域附近。在高、低速局部流场交界处,流速梯度变化剧烈,引起大尺度旋涡流动,局部区域涡量值较大。小尺度涡旋主要分布在叶片近壁面,主流区域上大尺度旋涡流动引起的高速液流冲击叶片表面,由于叶片几何结构空间扭曲,在叶片近壁面区域形成较小尺度下的涡旋结构。主流区域大尺度涡旋携带的流动能量逐渐传递到小尺度涡旋,由于叶片壁面区域、角隅区域处所形成的小尺度涡运动方向与主流涡运动方向有所不同,方向相同的小尺度涡旋对于主流区域上整体涡旋运动起到促进作用,而方向相反的小尺度涡旋对于主流区域上整体涡旋运动起到阻碍作用,在流体摩擦的作用下,考虑流体的粘滞损耗作用导致流动能量损耗。
4 PIV试验及数据处理
4.1 试验测量系统
为了验证仿真结果的准确性,基于粒子图像测速技术设计并搭建流场可视化试验台。试验台主要由机械系统、光学系统和图像采集系统组成,见图6。机械系统主要由1.1 kW变频调速电机、联轴器、转速测量仪及制动装置组成,用于液力变矩器动力驱动和载荷施加,并记录泵轮输入轴转速和涡轮输出轴转速。光学系统采用西安远讯光电科技有限公司生产的型号为PT-532- 1.5 W-L的激光器,可提供最大功率1.5 W、波长532 nm、扇面张角为90度的激光片光,片光厚度可达2 mm,使用前先预热,将液力变矩器待测流场区域照亮。图像采集系统采用广州市元奥仪器有限公司生产的型号为FR- 340- 10G图像记录系统及配套软件,相机帧频为338 fps,采集液力变矩器内部流动图像。试验样机为循环圆有效直径为315 mm的透明型液力变矩器,按实际液力变矩器大小以1:1比例制作,材质选择为有机玻璃,试验样机的壁厚为2 mm,避免引入较大的光路折射误差和图像畸变等问题。
4.2 图像采集与标定
以蒸馏水作为流动介质,选取直径为1.5 μm的PSP示踪粒子投入流场进行试验测量,保证粒子浓度符合图像采集要求[25]。通过变频调速电机控制泵轮输入转速为200 r/min,合理布置高清CCD相机空间位置,保证相机光轴垂直激光平面,可采集清晰的涡轮流道内部二维切面流场视频,经图像分帧处理选取连续两帧图像,在不考虑丢帧的情况下,根据相机帧频确定连续两帧图像之间的时间间隔为0.002 96 s。原始采集图像如图7所示,通过图像灰度化增强、降噪处理等图像预处理方法提高图像质量以保证后续流场参数的计算精度。图像标定精度决定流场参数提取精度。通过图像外标定方法获取图像放大率,图像预处理后采用Canny边缘检测算法识别图像边缘特征[26],提取涡轮外环多段半径数值,如图8(a)所示,将检测的半径均值与实际外环半径数值进行对比,获得的图像放大率为0.191 mm/px。标定结果见表1。

图6 PIV试验系统
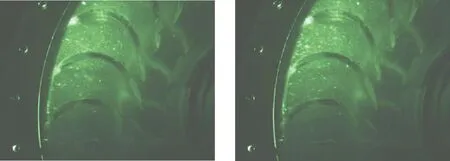
(a)第1帧 (b)第2帧

(a)半径检测 (b)实际尺寸
基于归一化递归互相关算法提取涡轮流场参数[27]。为了节省计算时间,只取涡轮单独流道为计算区域,其他流场区域进行掩膜处理,提取流速场和涡量场,如图9所示。为了定量验证CFD仿真结果的准确性,以涡轮中心为圆心,对涡轮单独流道进行圆弧等分划分,在流道中间区域水平位置提取8个等分点,如图9所示,提取等分点处流速值和涡量值,见表2和表3。

表1 标定结果

(a)流速等分点

(b)涡量等分点
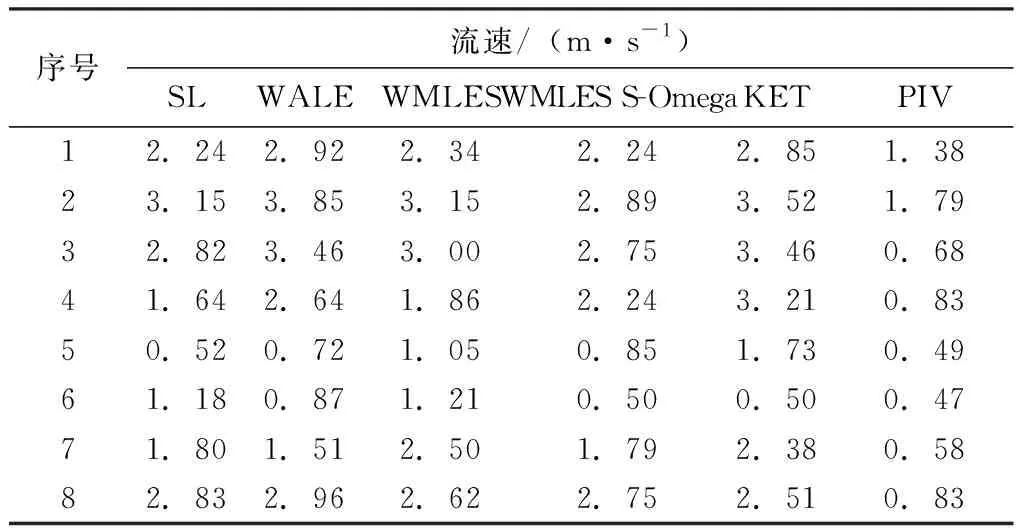
表2 涡轮单流道流速场中间截面流速值

表3 涡轮单流道涡量场中间截面涡量值
5 结果与讨论
5.1 流速场及涡量场
为了便于仿真与试验结果对比分析,截取涡轮单流道流场仿真结果,如图10所示。从流速场整体结构来看,不同湍流模型仿真结果中涡轮流场均呈现明显的旋涡流动,但是旋涡结构特征及涡心位置均不同,差异性明显。SL模型涡心分布在靠近叶片吸力面的中间位置处,呈现为“鞋垫状”的旋涡结构;WALE模型涡心向右下方偏移,相较于SL模型,其呈现为“反鞋垫状”的非包容型旋涡结构,且压力面处的高流速区域相对于其他模型仿真效果更加明显。WMLES模型涡心居中且靠近吸力面,呈现为纵向垂直状的“心脏形”旋涡结构,其下方的高流速区域相较于其他模型更加明显,且流速值较高。WMLES S-Omega模型涡心位置与WMLES模型接近,但是封闭状的旋涡结构不明显,低速区扩展到吸力面靠近出口位置。KET模型形成了两个涡心,与其他模型仿真结果均不相同,两个涡心在空间布局上形似“葫芦状”,较大的旋涡靠近主流区域中部,较小的旋涡位于其左上方靠近吸力面,它们的旋转方向相同,都是逆时针方向。
由于来自泵轮的高速流体冲击涡轮,涡轮入口处叶片吸力面与外环的交汇区域内出现大范围高速区,WALE和KET模型仿真结果中所呈现的高流速区域范围分布大,流速在3.8~4.6 m/s,如图10(a)所示,这与PIV试验结果中的B区域相对应,流速为1.7~3.0 m/s。SL和WMLES模型在低速区域仿真结果类似,流速在0.32~0.85 m/s,如图10(a)所示。对比PIV试验结果,如图9(a)中D区域存在明显低速区,流速为0.44~0.55 m/s。WMLES和WMLES S-Omega模型能够捕捉到叶片近壁面区域小尺度涡旋结构,WALES模型仿真结果中在涡轮流道压力面附近存在明显的高流速区,流速在3.7~4.4 m/s,与PIV的试验结果接近,如图9(a)中C区域所示,流速为1.7~2.8 m/s,而WMLES S-Omega模型在该区域上流速过于平滑且数值偏低,仿真结果失真。
从涡量场结构分布来看,采用5种亚格子湍流模型对叶片近壁面流场仿真结果类似,但是主流区域上涡量场结构分布差异明显,WALE模型在主流区域上的仿真结果存在两个高涡量场结构,呈左右分布,但左侧高涡量场区域分布范围较大。WMLES模型高涡量场结构主要集中在主流区域偏下方位置处,呈横向分布。KET模型仿真结果存在两个高涡量场结构,分布范围较大的高涡量场结构靠近吸力面一侧,分布范围较小的高涡量场结构位于主流核心区域,SL和WMLES S-Omega模型在主流区域上不存在明显的高涡量场结构,如图10(b)所示。对比PIV试验结果,如图9(b)中F、G、H区域上存在高涡量场结构,且涡量分别为582.17~793.42 s-1、425.41~596.79 s-1、471.48~612.37 s-1。针对F区域,数值模拟结果与试验结果不对应,这是因为PIV试验测量中液力变矩器外环与涡轮叶片交汇处出现明显的反光现象,如图7所示,因此导致PIV涡量场计算结果失真。针对G区域,WMLES模型仿真结果与PIV试验结果相近,涡量为475.47~840.36 s-1。针对H区域,KET模型仿真结果与PIV试验结果一致,涡量为426.37~782.46 s-1。

(a)流速 (b)涡量
为了量化对比数值模拟与试验测量结果,参照试验测量结果图9,将涡轮单独流道流场仿真结果进行等分圆弧划分,在流道中间区域水平位置提取8个等分点,保证数值模拟结果与试验测量结果比对点保持一致。由于文章篇幅有限,数据处理方法相同,以SL湍流模型仿真结果为例,提取流场8个等分点上的流速值和涡量值,如图11所示,仿真数据提取结果见表2和表3。

(a)流速场等分点 (b)涡量场等分点
图12为数值模拟结果与PIV试验结果对比图。从流速数值分布趋势上来看,如图12(a)所示,5种亚格子湍流模型仿真结果与PIV试验结果分布走势一致,但仿真数值均大于试验数值,这与PIV流场图像标定精度有关。综合数据曲线整体趋势和测量数据点数值两个方面,WMLES S-Omega模型仿真结果与PIV试验结果更加接近。从涡量数值分布趋势来看,无明显规律,尤其是数据点3~6上涡量数值发生巨大跃变,如图12(b)所示,这是由于制动工况下涡轮流道主流区域上出现大尺度旋涡流动,流场梯度剧烈变化,在整体旋涡运动进程中同时伴随着多尺度涡系结构的碰撞、交融和混合等动力学过程,导致涡量数值杂乱无章。从离散点的涡量数值比对来看,WMLES S-Omega模型仿真结果与试验结果误差最小。
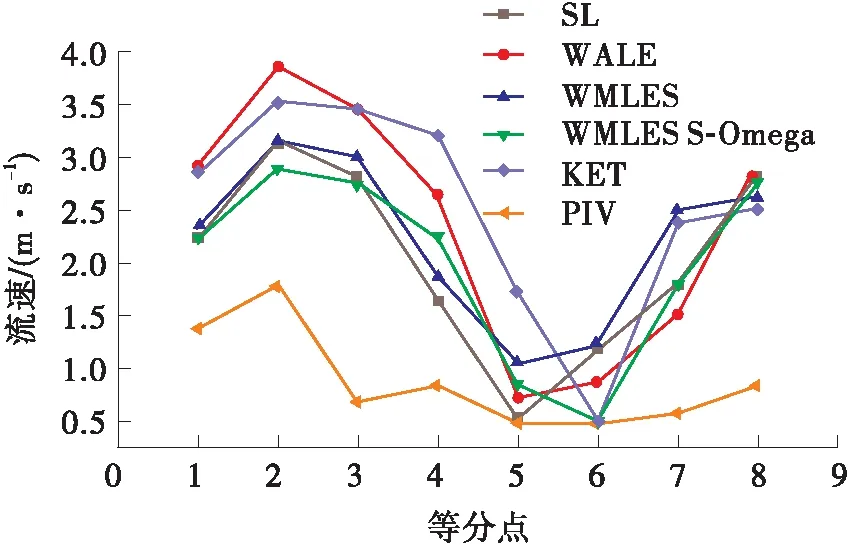
(a)流速
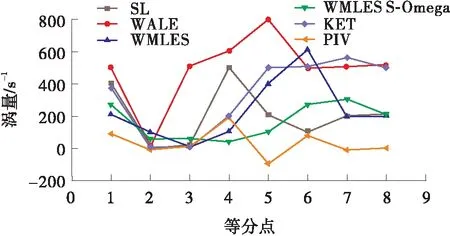
(b)涡量
6 结论
(1)从流速场结构分布来看,采用SL和WMLES模型流场仿真结果类似,采用WMLES模型对叶片压力面高流速区域仿真效果较好,与PIV试验一致。从流速数值定量角度来看,WMLES S-Omega模型与PIV试验结果最接近。
(2)从涡量场结构分布来看,5种亚格子湍流模型对于叶片近壁面涡量场仿真相近,但是主流区域上涡量场结构分布差异性较大。WMLES模型仿真结果所呈现的高涡量区域与PIV试验结果最接近。从涡量数值定量角度来看,WMLES S-Omega模型仿真结果与试验结果误差最小。
(3)从三维涡时空结构分布角度来看,WMLES和WMLES S-Omega模型能够时空再现叶片近壁面丰富的三维涡结构。KET模型能够捕捉到涡轮叶片尾迹区域上明显的脱落涡结构,对于泵轮与涡轮无叶栅区域上的三维涡结构仿真效果较好。
