考虑概率参数相关性的电动车悬置系统分析

吕辉 赵嘉伟 毛海宽 黄晓婷

(1. 华南理工大学 机械与汽车工程学院，广东 广州 510640； 2. 重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054； 3. 广州城市理工学院 汽车与交通工程学院，广东 广州 510800)

汽车动力总成悬置系统(PMS)通过悬置元件连接汽车动力总成和车架或车身。性能良好的PMS能显著改善汽车舒适性和噪声品质[1]。对电动汽车而言，由于驱动电机工作时会产生高频激励和电磁脉冲，PMS提供的减振降噪作用显得十分重要。受到加工制造、安装误差、工况变化等复杂因素的影响，电动车PMS不可避免地存在着各种不确定因素[2]。因此，在实际工程中，开展电动车PMS固有特性的不确定性分析具有重要的工程意义。

近年来，基于不确定性分析的PMS研究已取得很大进展。当系统参数样本充足时，常用概率模型[3]来描述系统参数的不确定性。谢展等[4]将悬置刚度等关键参数处理为概率变量，结合多目标优化方法，对汽车PMS进行了稳健性设计。吴杰等[5]用概率参数描述悬置系统设计变量和惯性参数的不确定性，建立了汽车PMS可靠性优化模型。针对系统参数信息匮乏而难以构建概率模型的情形，区间模型和模糊模型等非概率模型已被引入不确定性研究领域并受到了广泛的关注[6]。Cai等[7]基于切比雪夫多项式和顶点法，提出了一种计算PMS固有特性区间响应的快速方法；吕辉等[8]提出了模糊摄动-中心差分法用于高效求解PMS固有特性的模糊响应。

上述研究工作均建立在系统不确定参数相互独立的前提假设之下。然而，在工程实际中，机械结构不确定参数往往存在相关性[9]。例如，电动车PMS中一般采用橡胶悬置，而橡胶悬置的三向刚度明显存在着一定的相关性。这时，如果假设悬置三向刚度参数之间相互独立，则必然会引起一定的分析误差。针对PMS非概率参数存在相关性的问题，吕辉等[10]引入多椭球凸模型描述了PMS悬置三向刚度的相关性；随后又引入多维平行六面体模型有效处理了系统中同时存在相关性和独立性不确定参数的问题[11]。这些研究均将系统参数视为非概率变量。

可以看出，现有的PMS不确定性分析方法主要适用于非概率不确定情形，目前还未能有效处理概率参数存在相关性的情形。有鉴于此，文中针对电动车PMS概率参数存在相关性的情形开展了系统固有特性的分析研究，以期为该复杂情形下的电动车PMS后续优化设计提供理论基础和参考。

1 电动车PMS固有特性计算

1.1 固有频率计算

建立电动车PMS的简化动力学模型时，一般将电机和减速器等总成视为6自由度刚体；而橡胶悬置则简化为三向正交的弹性元件模型。电动车悬置系统常使用三点布置形式，图1为某电动车的PMS模型[12]。

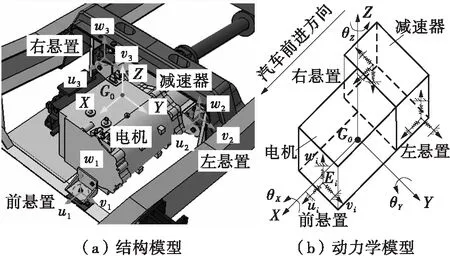
图1 电动车PMS模型

PMS模型坐标系的具体定义可参见文献[12]，系统的自由振动微分方程为

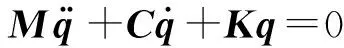
(1)

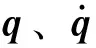
由于悬置阻尼对PMS固有特性影响较小[7]，因而文中忽略阻尼特性的影响，即把PMS视为无阻尼振动系统。

通过式(1)可求得PMS的6阶固有频率fj=ωj/(2π)及相应的系统振型φj=[φ1j,φ2j,…,φ6j]T(j=1,2,…,6)。

1.2 解耦率计算

当系统以第j阶固有频率fj振动时，分布到第k个广义坐标上的能量百分比为[13]：

(2)

式中，φkj为φj的第k个分量，Mkl为质量矩阵第k行第l列的元素。

系统第j阶模态下的解耦率为

(3)

当dj=100%时，表示系统第j阶振动时能量全部集中在某个广义坐标上，该阶振动完全解耦。

2 考虑概率参数相关性的PMS固有 特性分析

2.1 概率变量相关性的描述与处理

假设系统存在n维正态分布概率变量构成的向量X=[X1,X2,…,Xn]T，其均值和方差向量分别表示为μ(X)和σ2(X)，X中任一概率变量Xq(q=1,2,…,n)的均值和方差分别表示为μ(Xq)和σ2(Xq)。当正态概率向量X中任意两个变量Xi和Xj之间存在相关性，则它们的相关性可以用相关系数矩阵来描述：

(4)

式中，相关系数ρij表示Xi和Xj之间的Pearson相关系数。当ρij=0时，Xi和Xj相互独立;当ρij>0时,Xi和Xj正相关；当ρij<0时,Xi和Xj负相关。根据相关系数矩阵可以得到协方差矩阵：

(5)

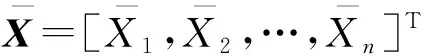
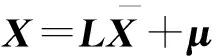
(6)

由于协方差矩阵CX为对称矩阵，则矩阵L可通过对CX进行Cholesky分解得到：

CX=LLT

(7)

在确定各维概率变量的前两阶统计矩和相关系数之后，通过式(6)可以实现n维相关正态概率向量X和n维独立正态概率向量相互转化。相关系数矩阵ρ中的元素ρij取值范围为[-1,1]，不同取值反映了不同情形下的变量相关性。

2.2 基于蒙特卡洛法的计算方法

电动汽车PMS系统参数受到加工、装配误差和材料老化等因素的影响，其参数取值具有一定的随机性，一般采用正态分布的概率变量描述。对于具有三个悬置的电动车PMS，同一悬置的三向刚度之间通常存在一定的相关性，而不同悬置之间的刚度参数则相互独立。此时，系统悬置刚度参数的相关系数矩阵ρK可表示为

(8)

为方便表述，概率不确定情形下PMS系统固有频率和解耦率函数统一采用g=g(X)表示。其中，系统概率参数X的相关性用相关系数矩阵ρK描述。

蒙特卡洛法(MCM)在样本规模足够大的情况下能获得较高的计算精度。基于MCM求解考虑概率参数相关性的PMS固有特性的基本过程如下。

(1)根据n维具有相关性的概率向量X的相关系数矩阵，以及各变量的边缘分布参数，通过式(5)计算得到协方差矩阵CX，对其进行Cholesky分解，得到下三角矩阵L;

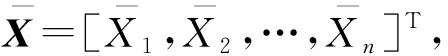
(4)计算相关样本矩阵XS中每一组样本数据对应的系统固有频率及解耦率，得到P组系统响应g(XS)。

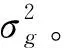
MCM的计算通常需要较大的样本量来保证计算精度，其计算效率有时难以满足工程实际需求。因此，下文接着提出一种较为高效的数值方法。

2.3 基于稀疏网格数值积分的矩估计法

n维概率向量X输入下PMS固有特性的分析，可以转化为概率响应函数g=g(X)前两阶矩的求解。g(X)前两阶矩的公式如下：

(9)

(10)

式中，fX(X)为概率向量X的联合概率密度函数，Ω⊆Rn为X的积分域即定义域。

上述统计矩的计算要求在积分域Ω内进行多重积分，可以引入稀疏网格数值积分(SGNI)方法解决这一高维积分问题[14]。SGNI方法以Smol-yak算法为基础，通过特殊的张量积操作，将一维高斯积分节点构造为高维积分节点，进而将这些高维积分节点用于响应统计矩的估计。

首先考虑系统响应仅是单概率变量Y=ξ函数的情况，即g1=g(Y)。此时，式(9)和式(10)中系统响应统计矩可以通过高斯型积分计算：

(11)

(12)

式中，ξp和wp分别表示第p个高斯积分点所对应的节点值和权值，m为节点总个数。一维高斯节点和权值可以通过高斯-埃尔米特、高斯-勒德让和高斯-拉盖尔求积公式得到。

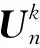
(13)

式中，k代表多维积分精度水平。k的值越大，说明积分精度就越高。|i|=i1+i2+…+in，ir(r=1,2,…,n)是对应于各维概率变量的多指数，它们决定了各维上所配置的积分节点数目mr，通常令mr=ir[16]。⊗为张量符号。

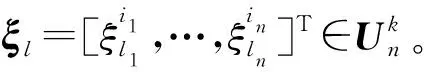
(14)

(15)

(16)

当精度水平为k时，每个维度上的节点最多为k+1，因而式(15)最多具有2k+1次代数精度。n维配置点个数N随着精度水平k取值的变化而变化，具体对应关系如下式[16]：

(17)

以一个9维问题为例，即n=9，令精度水平k=2时SGNI方法的积分节点总个数为181，为了达到相同的积分精度，直接数值积分法[17]所需的配置点数量为39=19 683。可见SGNI方法能以较少的积分节点获得较高的积分精度。

(18)

(19)

使用SGNI方法求解相关概率参数输入下的PMS固有特性的流程如下:

步骤1 根据X的概率分布和相关系数矩阵，分别由式(5)和式(7)求得协方差矩阵CX和相关性变换矩阵L;

步骤2 预先规定稀疏网格的精度水平k(k≥0),求出满足不等式k+1≤|i|≤k+n的多指数组合;

步骤3 基于多指数组合确定各维概率变量的积分节点数mr，根据各维概率变量的分布形式、参数以及积分节点数mr计算各维上相应的一维高斯积分点和权值;

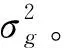
上述SGNI方法的分析过程可总结为如图2所示的求解思路。

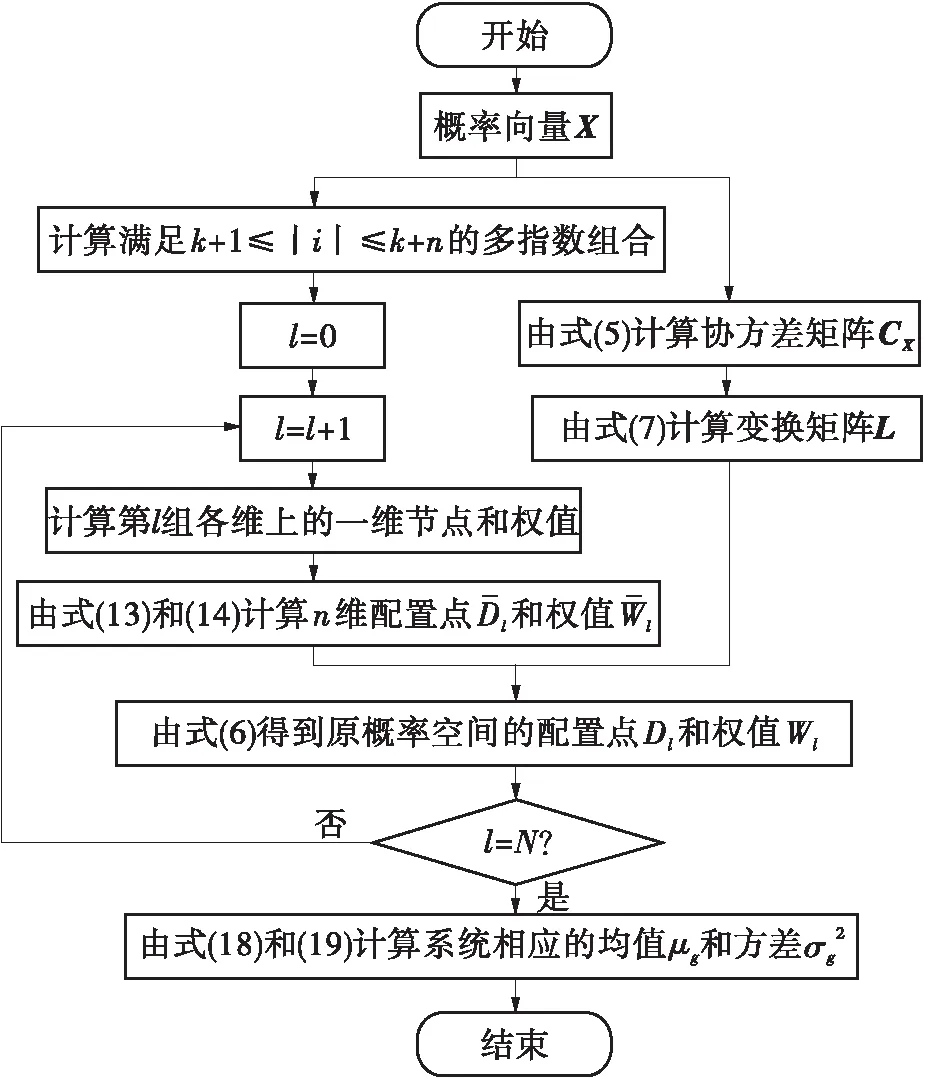
图2 SGNI方法流程图

3 算例分析

3.1 分析模型

以图3所示的某电动车PMS为例。系统的质量、转动惯量和惯性积如表1所示；表2和表3分别为悬置的初始静刚度以及它们在动力总成坐标系中安装位置；表4给出了悬置的安装角度。

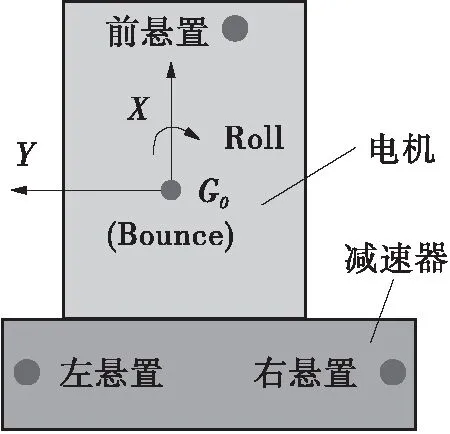
图3 某PMS分析模型

表1 电机总成质量、转动惯量与惯性积

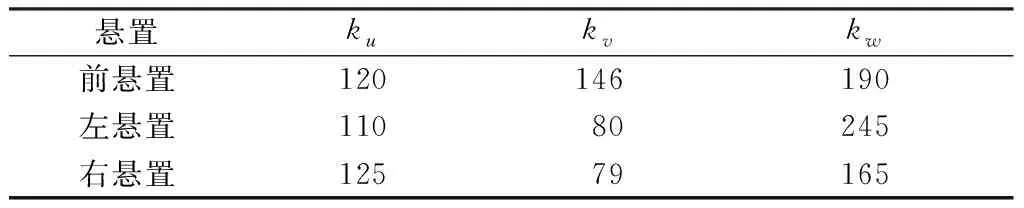
表2 悬置刚度

表3 悬置的安装位置

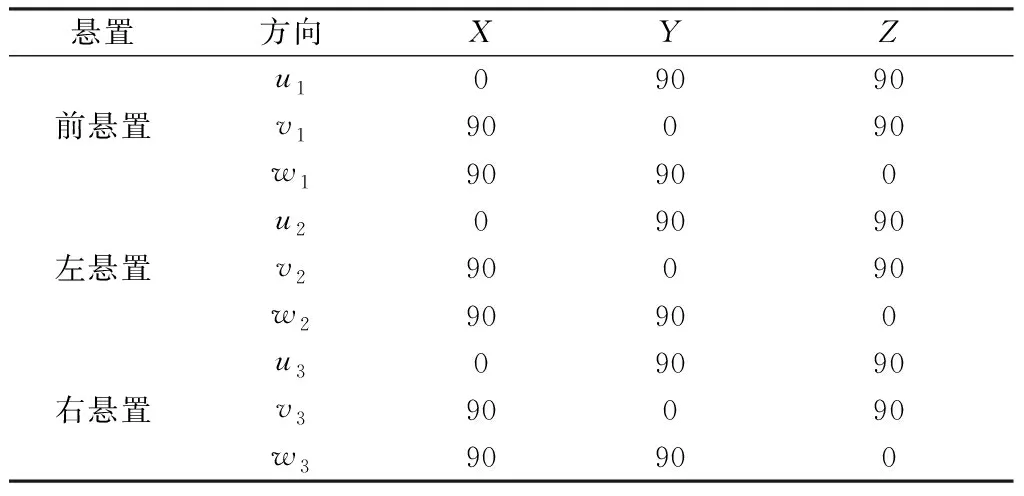
表4 悬置安装角度

3.2 考虑概率参数相关性的系统固有特性分析

电动车PMS的振动方向主要沿竖直方向(Bounce方向)和绕定转子中心线的旋转方向(Roll方向)，故本文中重点关注这两个方向的固有特性。在下文分析中，将Bounce方向的固有频率和解耦率分别记为fB和dB，Roll方向的固有频率和解耦率分别记为fR和dR。

为了研究系统参数相关性对系统固有特性的影响，同时考虑到悬置三向刚度参数存在明显的相关性，本文中选取悬置刚度参数作为研究变量。悬置刚度参数的不确定性采用最常用的正态分布概率变量来描述，且取变量的变异系数(即标准差与均值之比)CV=0.07。为方便分析，假设各悬置三向刚度参数的相关系数均为ρ，则系统刚度参数的相关系数矩阵可表示为

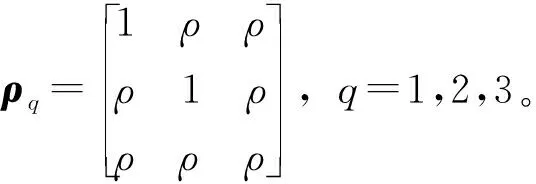
采用本文中提出的MCM和SGNI两种方法求解系统固有特性响应的前两阶矩，选取相关系数ρ=0.6的分析结果列于表5中。其中，对于SGNI方法，给出了两种精度水平下(k=2,3)的计算结果。表中e表示SGNI方法的计算误差，即两种方法计算值之差的绝对值与参考值的百分比，参考值为样本量为106的MCM方法计算结果。

在计算精度方面，由表5可以看出，当k=2时，SGNI方法求得的系统响应均值的计算误差均低于0.1%，而响应方差的计算误差均低于8%；当k=3时，计算误差进一步降低，均在1%之内。这表明SGNI方法具有较高的计算精度。此外，响应方差的计算误差明显大于响应均值的误差，这是因为SGNI方法对响应统计矩的求解误差随着统计矩的阶数增加而增加。另外，解耦率方差的计算误差明显大于固有频率方差的计算误差，主要原因在于系统解耦率对刚度参数的变化比固有频率更加敏感。

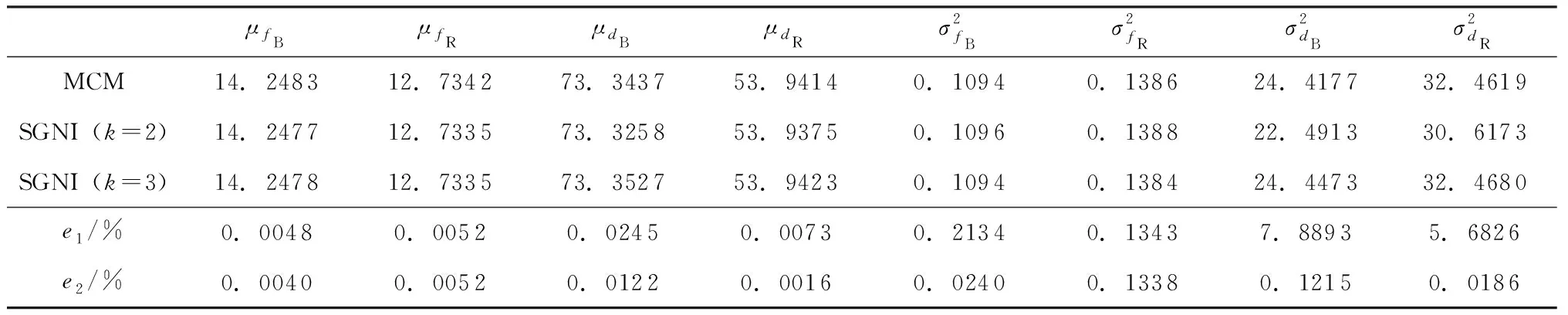
表5 前二阶矩估计和计算误差

在计算效率方面，表6给出了两种方法调用PMS固有特性响应函数g(X)的次数N0。可以看出，在计算响应前二阶矩时，MCM需要调用系统固有特性响应函数106次。而当k分别为2和3时，SGNI方法只需分别调用响应函数325次和2 925次。在同一台计算机上求解响应统计矩时，MCM方法耗时高达398.0 s；而当k为2和3时，SGNI方法分别耗时0.6 s和1.1 s。可见SGNI方法具有很高的计算效率。在后续优化设计中，上述统计矩的计算过程可能需要执行成百上千次，基于SGNI方法将能大幅提高优化设计效率。

表6 两种方法的计算效率

综上可知，在考虑概率参数相关性的电动车PMS固有特性响应前二阶矩的分析研究中，本文提出的SGNI方法有良好的综合性能，能较好地兼顾计算精度和计算效率，适用于后续的分析研究。

3.3 参数不同相关性的影响分析

考虑到各悬置的刚度参数相关性对系统固有特性的影响可能存在差异[11]。本文进一步探究概率参数不同的相关性对PMS固有特性的影响。通过灵敏度分析，发现对系统响应影响最为明显的一对参数为前悬置u、w方向的刚度参数Ku1和Kw1。下面分别考虑Ku1和Kw1的相关系数ρ=-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8等9种不同的相关情形下的系统响应。分析过程中假设其余的刚度参数为相互独立的不确定变量。

在不同相关情形下，基于MCM方法对悬置刚度参数Ku1和Kw1进行随机抽样，得到部分情形下的样本点如图4所示。可见，随着参数相关性的增强，样本值域逐渐变扁，面积变小，样本点更集中。极端情况下(ρ=±1)，样本值域将收束为一条直线。

除了系统响应的统计矩，工程应用中还比较关注系统响应的取值边界。根据工程常用的3σ准则，响应边界区间可以表示为[μ-3σ,μ+3σ]。

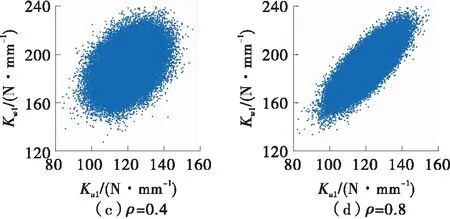
图4 部分情形下的样本点

图5(a)～(d)分别给出了不同相关系数下两种方法求得的系统响应上下边界结果。

从图5可以看出，在不同的相关系数下，SGNI方法求得的PMS固有特性响应边界与蒙特卡洛法求得的参考值具有很好的一致性。这说明SGNI方法能在计及概率参数相关性的情况下较好地预测系统响应的边界。此外，还可以得到以下结论：

(1)对于系统固有频率，随着相关系数从负到正变化，fB边界范围变化很小，而fR边界范围则出现了一定程度的扩张。总体上，不同相关情形下的系统固有频率响应边界范围差异不大。

(2)对于系统解耦率，随着相关系数的增大，dB和dR的边界范围均出现了明显缩窄，缩窄量随着相关系数的增大而增大。当参数存在较强正相关性(ρ=0.8)时，dB和dR的边界范围相比独立情形(ρ=0)时分别缩窄约10%和17%；当参数存在较强负相关性(ρ=-0.8)时，这两个方向解耦率的边界范围比参数独立情形分别扩大约6%和10%。总体上，不同相关情形下的系统解耦率响应边界差异比较明显，且相关系数的变化对于Roll方向解耦率范围的影响更为显著。

综上所述，对于本文所研究的电动车PMS，当考虑其概率参数的相关性后，系统固有频率、解耦率的响应范围出现不同程度的变化，计及不确定参数的相关性能得到更加合理的系统响应边界范围。此外，参数相关性对解耦率边界影响较大，在进行优化设计及相关研究时应予以充分关注。

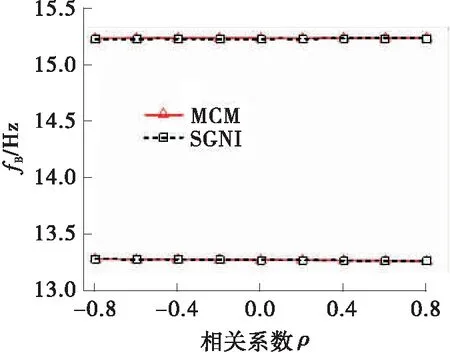
(a)fB边界

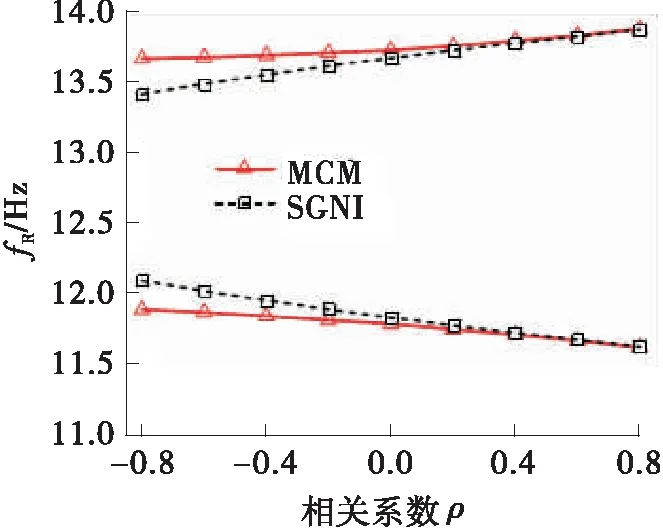
(b)fR边界

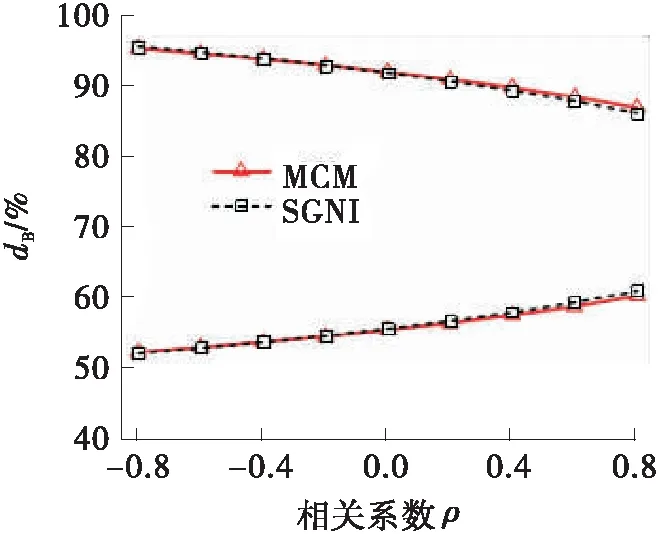
(c)dB边界

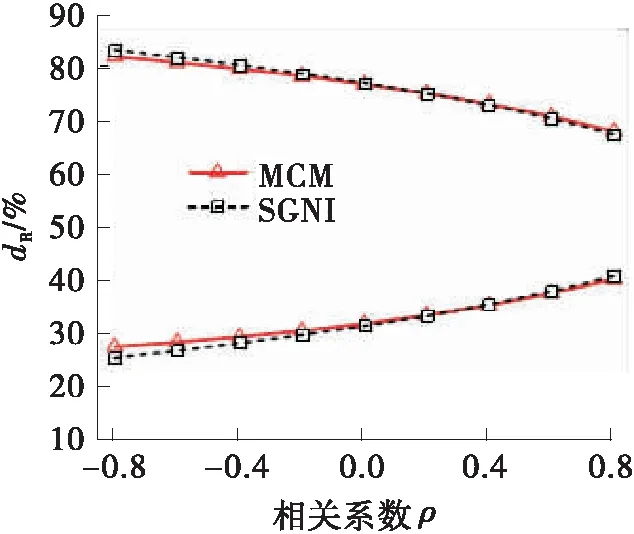
(d)dR边界

4 结论

针对电动车PMS不确定参数存在相关性的情形，本文提出了两种用于求解考虑概率参数相关性的PMS固有特性的分析方法。算例分析结果表明：(1)以MCM方法为参考，SGNI方法在求解PMS固有频率、解耦率的统计矩及响应边界方面具有良好的求解精度和较高的求解效率；(2)系统概率参数的相关性对PMS固有特性的响应边界具有较大影响，若不计及不确定参数的相关性，分析结果会产生较大的误差。本文方法主要开展了电动车PMS固有特性的分析计算，能为后续高效地开展PMS优化及改进工作提供基础。