应急排气管道对主烟囱中速度及气体混合的影响

2022-04-29郑金阁程卫亚刘伟富郝桂珍王晨潇郭浩城赵宇伦

辐射防护 2022年2期

郑金阁，程卫亚，刘伟富，郝桂珍，王晨潇，郭浩城，赵宇伦，陈凌

(中国原子能科学研究院，北京 102413)

烟囱的气态流出物监测工作涵盖取样截面高度选择、取样点位布置、气体样品分析等。为使气体样品更具代表性、监测结果更具可靠性，需保证取样截面位置处的气流速度和气体组分浓度分布等的均匀性[1-3]。部分通风设施在建设时，在主烟道内部设置应急排气管道，设施运行时，此细长圆柱形固体区域将产生绕流现象，对主烟道内的气体流场造成扰动，从而可能改变主烟道内流速及气体浓度分布情况[4-5]。

目前对于烟囱等通风管道内的气体混合均匀性的研究，主要借助于搭建比例模型开展实验或利用计算流体力学方法进行仿真模拟[4,6]。模型实验可以得到更为直观准确的数据结果，但需要搭建实验平台及购置测量仪器等，时间成本及经济成本较高。采用计算流体力学仿真，可在较短时间获得多种运行条件下的模拟结果，有效弥补模型实验的缺陷[7]。

基于计算流体力学的理论及烟囱管道相关的调研结论，按比例模型尺寸建模，选取三种风速条件，模拟内部的圆柱体应急排气管道对主烟道内速度和气体组分混合的影响情况，并与现有比例模型实验结果相对比，依据几何相似及动力相似准则，比例模型和实际烟囱流体雷诺数处于同一水平，研究结论可应用于实际烟囱，并可作为同类型烟囱及取样系统设计的参考。

1 模型建立及流体域离散

当前对于流体仿真计算最常采用有限体积法，从烟囱主体所在的固体区域内部提取气体流经区域作为计算域，而后对流体计算域进行网格划分，以得到离散化的控制体[8-9]。

基于现有实验平台，仿真采用1∶1比例进行几何建模，模型包含烟囱主体、排气混合箱及气体入口截面的示踪气体注入孔等。其中，圆柱形烟囱本体直径φ=600 mm，高度h=8 160 mm，内置直径80 mm、高8 160 mm的管道，长方体排气混合箱位于烟囱正下方，尺寸为2 200 mm×1 340 mm×980 mm。内部管道位于主烟囱内靠近壁面位置，其轴线与主烟囱轴线间距230 mm，与混合箱长边所在直线夹角60°，气体入口位于排气混合箱一侧。模型整体及内部管道布置情况见图1、2。

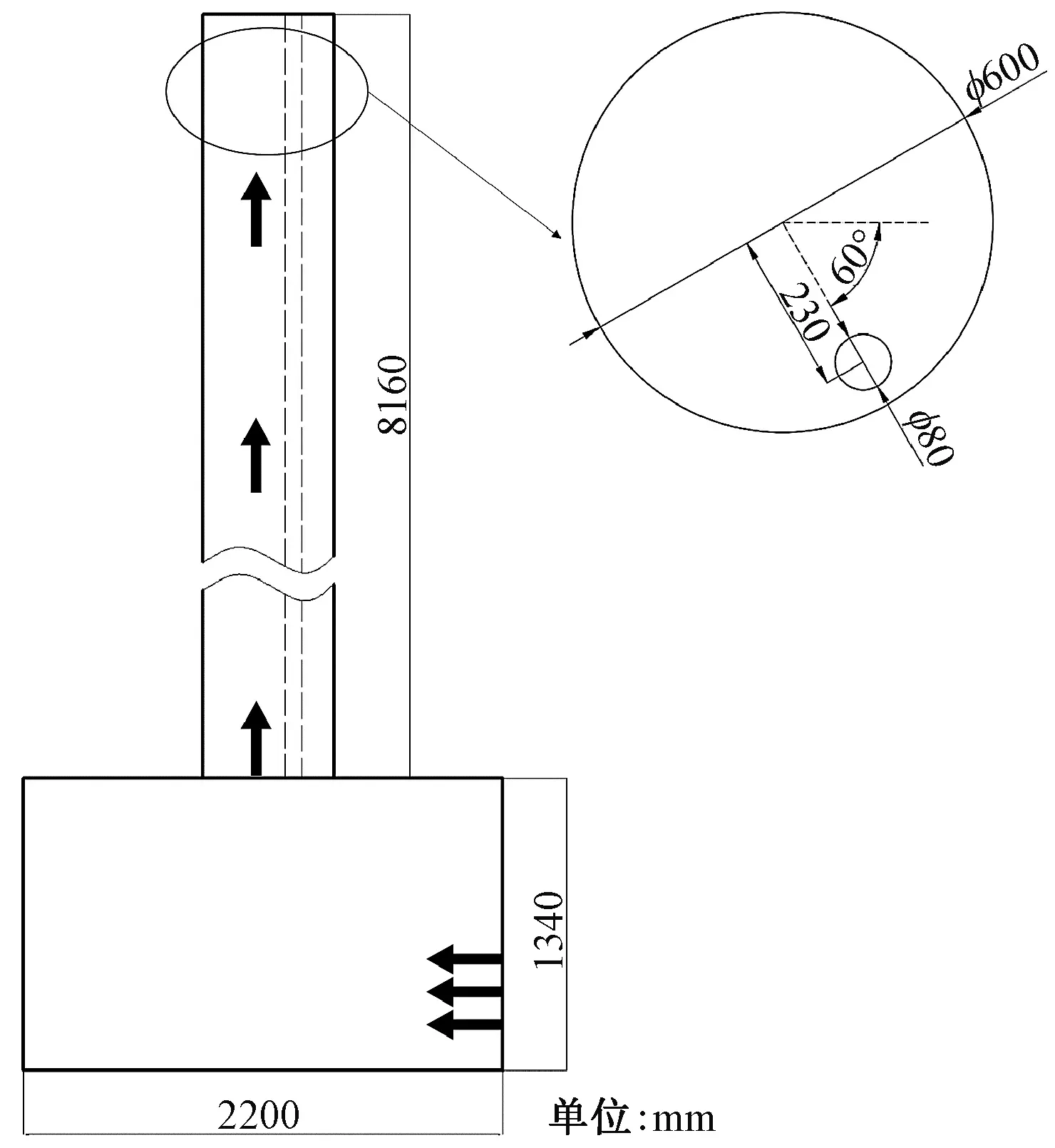
图1 烟囱几何模型示意图Fig.1 Schematic diagram of chimney geometric model

采用三维笛卡尔直角坐标系，原点位于烟囱主体与混合箱交界面的圆心点。为简化计算难度并提高网格划分质量，几何模型创建过程对内部管道固定支架、混合箱与烟囱主体法兰接缝等细节进行了忽略。每个监测截面设置13个监测点位，分布在截面圆心(1个)、距圆心122 mm处(4个)、距圆心212 mm处(4个)、距圆心274 mm处(4个)。监测点位置示意见图2。

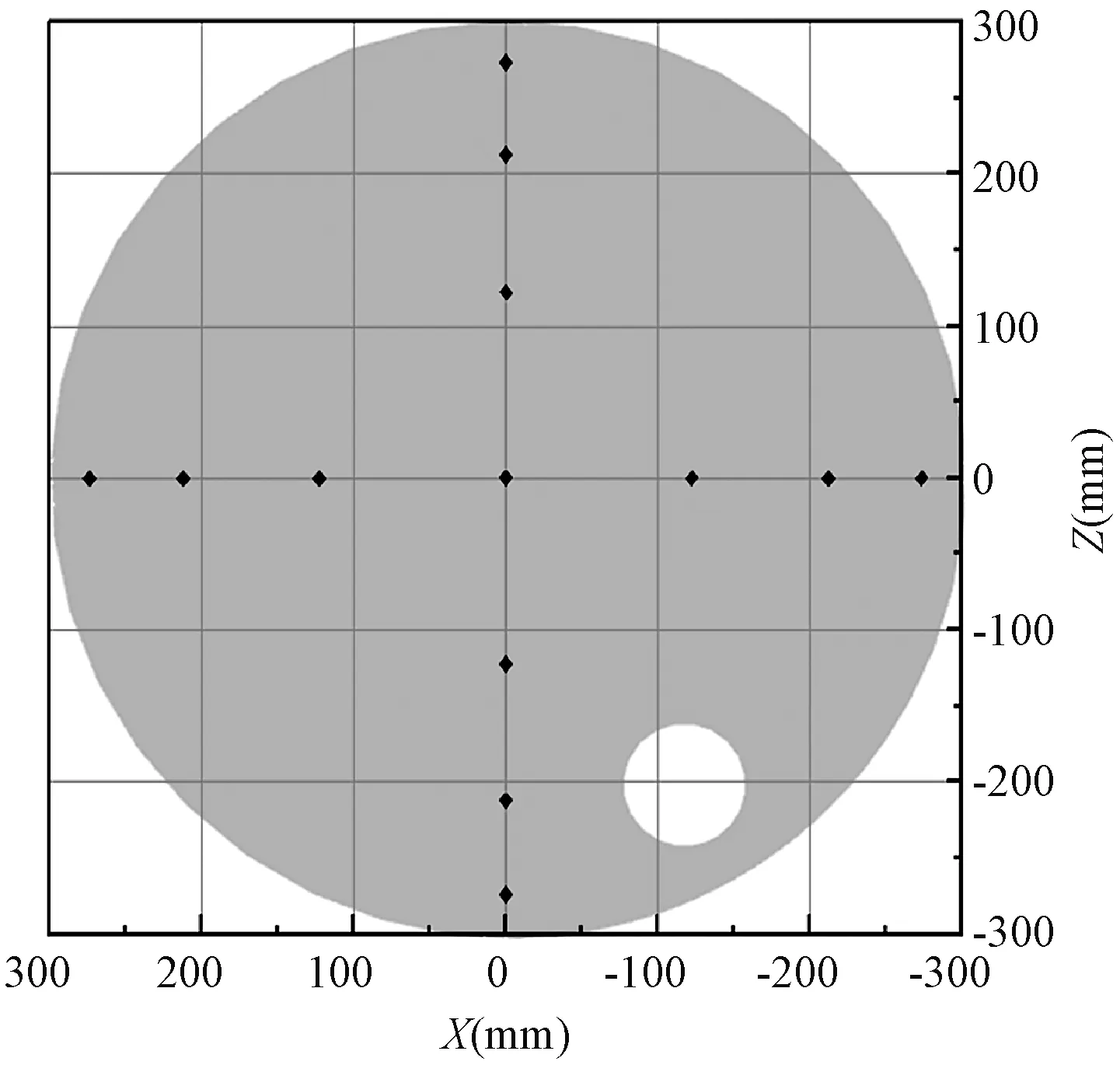
图2 监测点位置示意图Fig.2 Schematic diagram of monitoring points location

将待计算流体域划分为六面体与多面体结合的非结构化网格，以更好的描述几何模型细节[8-9]。在内部管道附近区域采用特征尺寸2.0 mm网格，烟囱主体及混合室内部流体区域采用特征尺寸40 mm网格，并划分5层边界层网格用以近壁面处的加密。

采用相同的方法及特征尺寸对无内部管道的烟囱模型进行网格划分。两模型网格划分及加密情况如图3所示。

图3 烟囱模型顶部出口位置网格划分示意图[(a)含内部管道，(b)无内部管道]Fig.3 Schematic diagram of the chimney model top exit point mesh [(a): with internal pipe, (b): without internal pipe]

2 边界设置及控制方程选择

主烟囱内气体平均流速分别为13.1、8.2及0.56 m/s，气体为冷排放，温度及压力与环境相近，视为不可压缩流体。空气及示踪气体入口设置为速度入口边界条件，烟囱顶部出风口为压力出口。烟囱主体内部流场的流动状态可由雷诺数Re计算得出，其表达式为:

(1)

式中，Re为雷诺数；ρ为气体密度，kg/m3；v为气体流速，m/s；μ为气体的动力粘度，N·s/m2；L为取样截面的特征长度，m。

对于含内部管道的烟囱结构，其过流断面特征长度L计算式为:

(2)

式中，A为过流断面面积，m2；c为截面周长，m；D与d分别为主烟囱及内部管道直径，m。

同理，对于无内部管道的烟囱结构，其过流断面特征长度L为直径D。

高、中、低三种风速下，两种模型主烟囱内部流场Re值均高于10 000，视为充分发展的湍流。排气入口处边界条件的湍流参数选取湍流强度及特征长度。湍流强度I由下式计算:

I=0.16Re-1/8

(3)

流体连续性控制方程即质量守恒方程:

(4)

式中，t为运动时间，s；u、v、w分别为速度矢量在x、y、z方向的分量，m/s。

根据动量守恒定律，可写出x、y、z三个方向的动量守恒方程，即

(5)

式中，p为流体微元体上的压力；τxx、τxy和τxz等为因分子粘性作用而产生的作用在微元体表面上的粘性应力τ的分量；Fx、Fy和Fz为微元体上的体积力。

烟囱内流场处于湍流状态，采用标准形式的k-ε双方程模型进行仿真，包含湍流脉动方程k方程与湍流耗散方程ε方程，通过增加两个附加方程以求解Navier-Stokes方程。示踪气体SF6注入后，与空气组成烟囱内的气体成分，利用组分输运方程计算得烟囱内取样截面位置的SF6质量分数[10]。

仿真过程涉及到的密度值ρ皆为常数。示踪气体SF6的相对分子质量为146，过程中考虑重力作用。求解过程采用ANSYS Fluent软件完成，通过足够次数的迭代，计算达到收敛。

3 仿真结果分析

自烟囱主体底部开始，随高度升高依次设置9个监控截面，分别位于1 m(1.7D)、2 m(3.3D)、3 m(5.0D)、4 m(6.7D)、5.1 m(8.5D)、5.3 m(8.8D)、6.1 m(10.2D)、6.9 m(11.5D)、8 m(13.3D)。依据ISO 2889—2010及ANSI/HPS N13.1—2011中提供的取样截面混合均匀性判定指标[3,11-12]，对于流场和气体组分的评价指标包括取样截面内的平均气旋角度、截面中心2/3以上面积内的速度变异系数COV、截面中心2/3以上面积内的示踪气体浓度变异系数COV、示踪气体浓度较平均值的最大偏差等。其中气旋角度用以评估取样截面位置是否存在旋流，随取样截面升高，气体浓度最大偏差与变异系数COV变化趋势一致，因此结果分析部分以速度及示踪气体浓度的变异系数(COV)表征截面混合均匀性。每个监测截面选择9个监测点位进行COV计算，覆盖截面中心2/3以上面积，分别为截面圆心(1个)、距圆心122 mm处(4个)、距圆心212 mm处(4个)。5.1 m(8.5D)处截面对应于实际烟囱25.5 m处截面，为取样截面实际所在位置，因此研究中做重点考虑。

对于速度及示踪气体浓度，其COV计算公式均为:

(6)

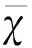
3.1 高风速仿真结果分析

主烟道内平均风速13.1 m/s，有无应急排气管道时内部流场皆处于充分湍流，提取两模型各自9个高度处的速度及示踪气体浓度数据，计算截面中心2/3面积内的变异系数COV。以截面所在高度为横坐标，两模型速度COV及SF6浓度COV数据对比如表1、图4所示。

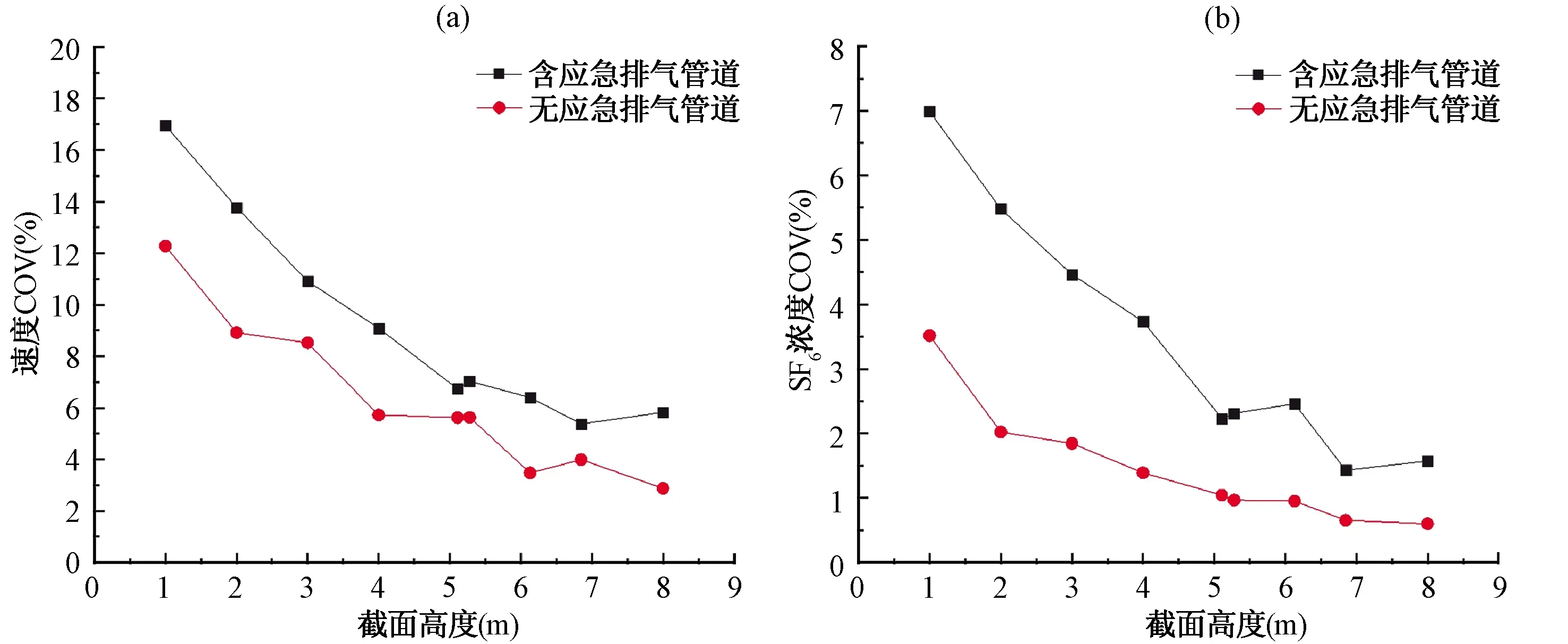
图4 高风速下有无应急排气管道时混合均匀性指标对比(a：速度COV对比，b：SF6浓度COV对比)Fig.4 Comparison of mixing uniformity index with or without emergency exhaust pipe under highwind speed (a: velocity COV; b: SF6 concentration COV)

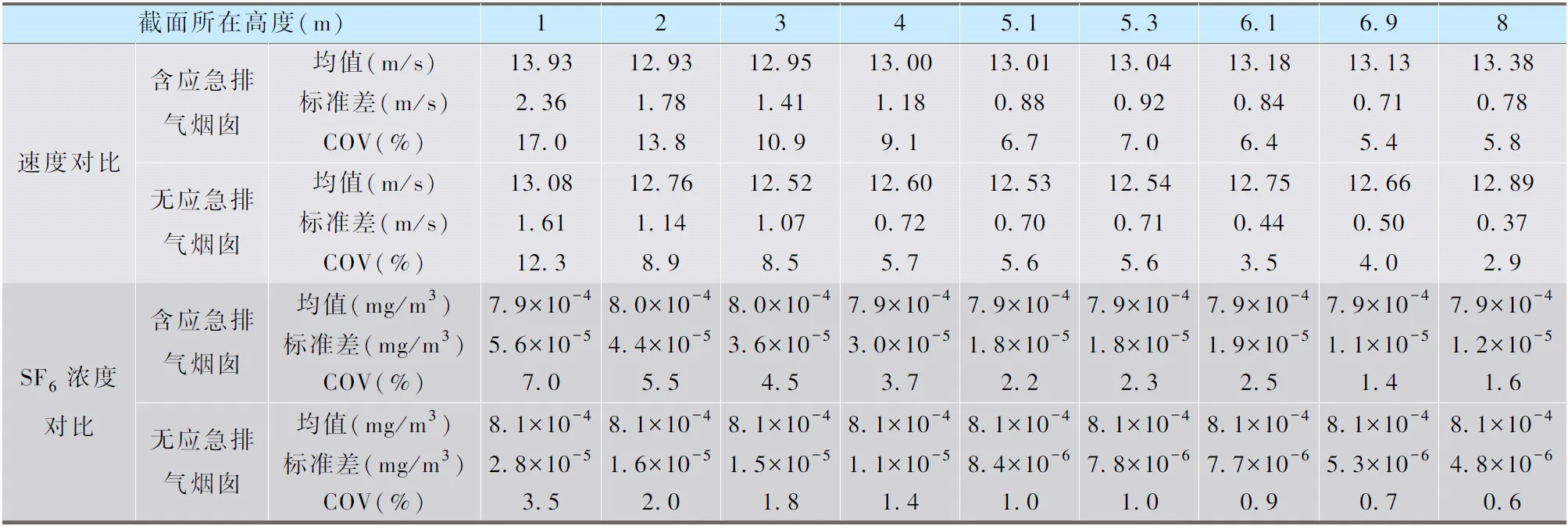
表1 高风速下有无应急排气管道时混合均匀性指标对比Tab.1 Comparison of mixing uniformity index with or without emergency exhaust pipe under high wind speed

主烟道内高风速条件下，无应急排气管道可带来更低的速度COV及SF6浓度COV，对各高度下的COV取平均值后做差，可得，移出主烟道内部的应急排气管道后，速度COV将降低2.8%，SF6浓度COV降低2.0%，主烟囱内的气体可以达到更好的混合均匀性。若选取5.1 m高度处的截面进行取样监测，有无应急排气管道时，该截面的气体流速及示踪气体分布情况如图5所示。据图可知，在应急排气管道附近区域出现了速度及示踪气体分布的扰动，在当前风速条件下，此扰动对于该位置的气体混合是不利的。

图5 高风速下有无内部管道时速度及SF6分布对比[(a)、(b)：截面速度分布情况，(c)、(d)：SF6浓度分布情况]Fig.5 Comparison of velocity and SF6 distribution under high wind speed [(a), (b): velocity distribution, (c), (d): SF6 concentration distribution]

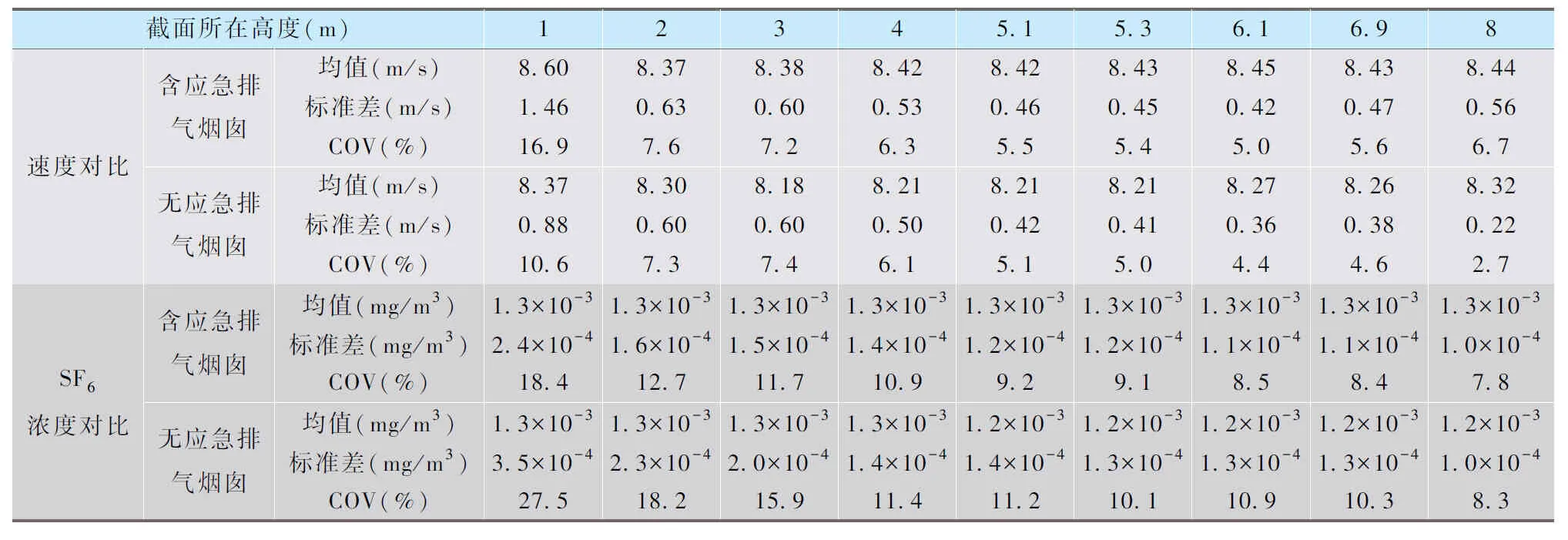
表2 中风速下有无应急排气管道时混合均匀性指标对比Tab.2 Comparison of mixing uniformity index with or without emergency exhaust pipe under medium wind speed

3.2 中风速仿真结果分析

依同样方法可绘制中风速下两模型速度COV及SF6浓度COV数据对比表(表2)、对比图(图6)、5.1 m高度截面的气体流速及示踪气体分布图(图7)。

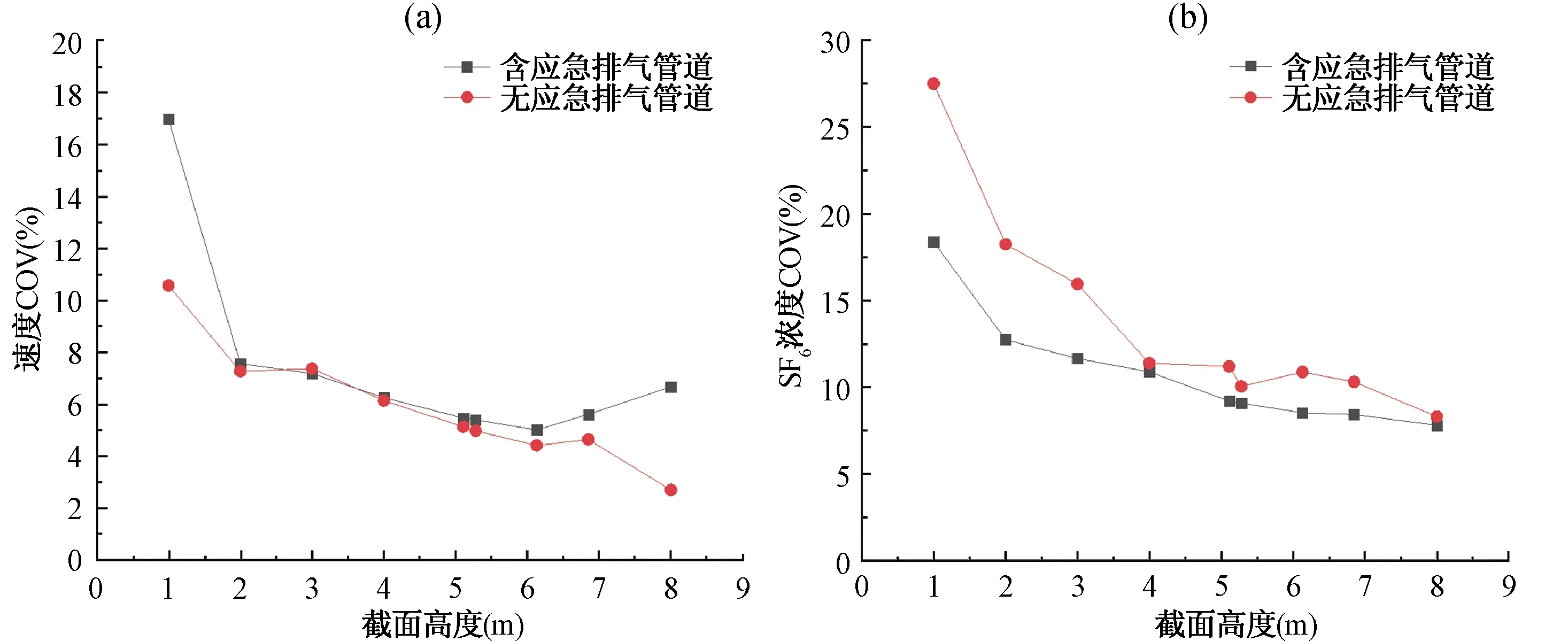
图6 中风速下有无应急排气管道时混合均匀性指标对比[(a)：速度COV对比，(b)：SF6浓度COV对比]Fig.6 Comparison of mixing uniformity index with or without emergency exhaust pipe under medium wind speed [(a): velocity COV; (b): SF6 concentration COV]

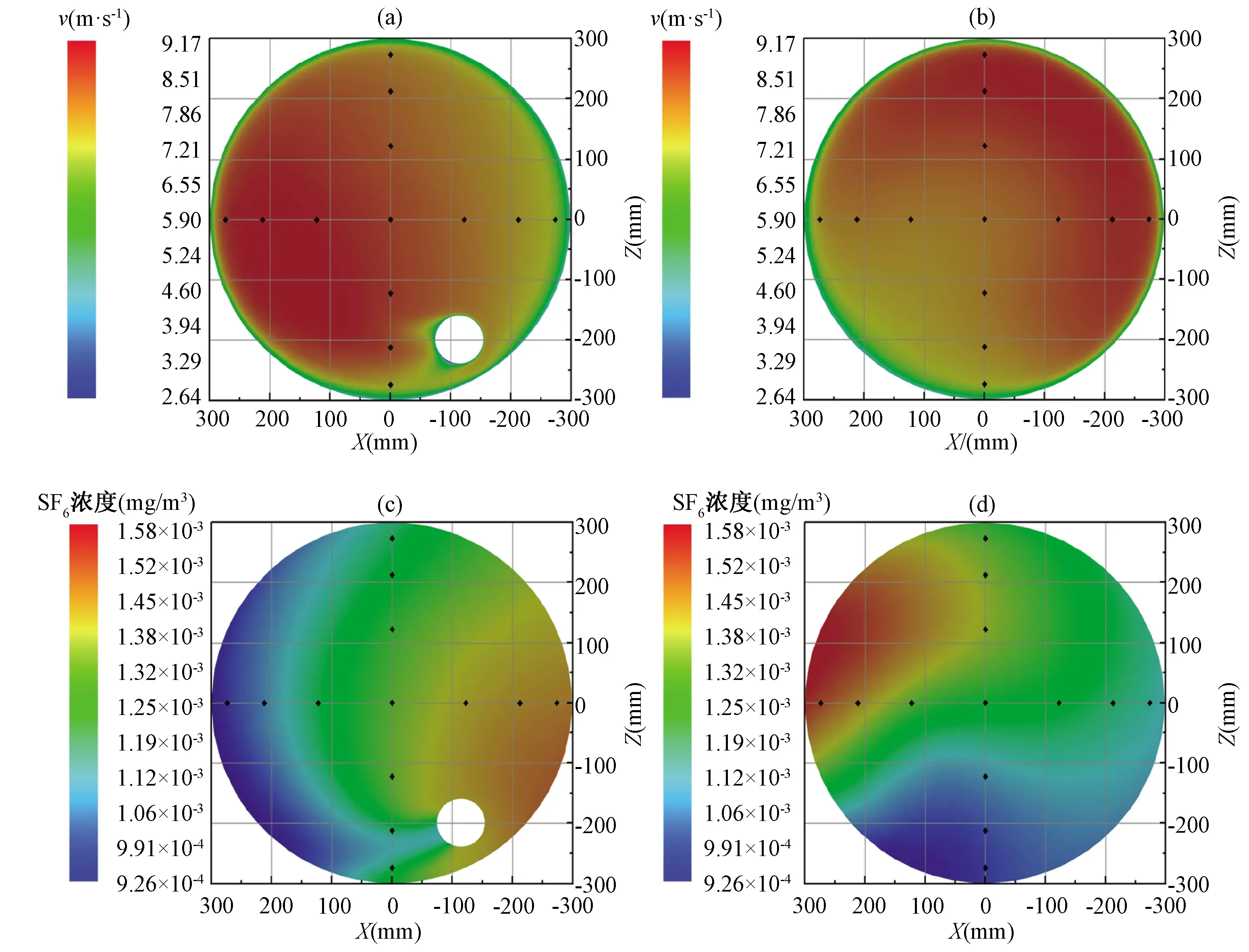
图7 中风速下有无内部管道时速度及SF6分布对比[(a)、(b)：截面速度分布情况，(c)、(d)：SF6浓度分布情况]Fig.7 Comparison of velocity and SF6 distribution under medium wind speed [(a), (b): velocity distribution, (c), (d): SF6 concentration distribution]

主烟囱平均风速8.2 m/s时，无应急排气管道利于速度均匀分布，其各截面平均COV相比含应急排气管道的情况降低1.5%，自2 m到7 m，速度COV值不存在显著差距；SF6浓度分布在无应急排气管道时呈现稍差的均匀性，COV值相比含应急排气管道的情况升高3.1%，且在低高度截面存在较明显差异。

3.3 低风速仿真结果分析

低风速下两模型速度COV及SF6浓度COV数据对比表(表3)、对比图(图8)、5.1 m高度截面的气体流速及示踪气体分布图(图9)如下所示。

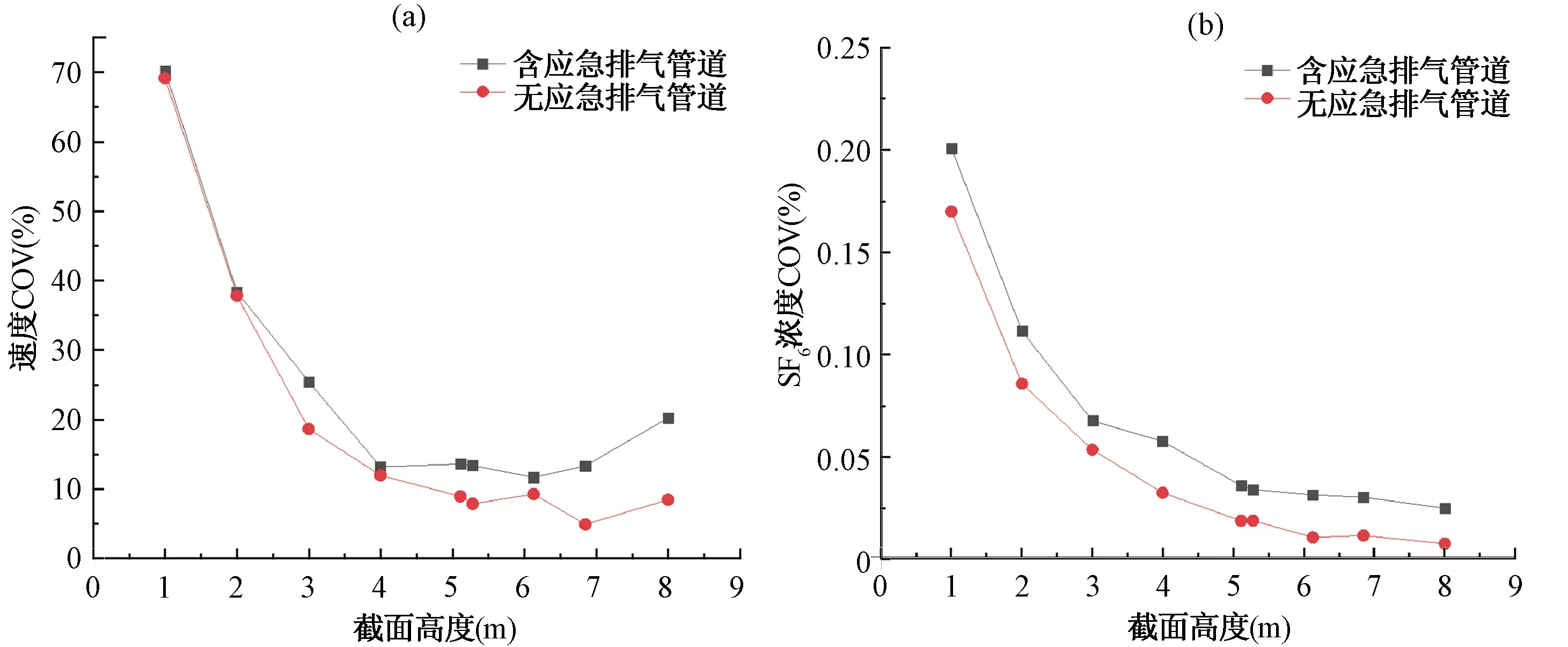
图8 低风速下有无应急排气管道时混合均匀性指标对比[(a)：速度COV对比，(b)：SF6浓度COV对比]Fig.8 Comparison of mixing uniformity index with or without emergency exhaust pipe under low wind speed [(a): velocity COV; (b): SF6 concentration COV]

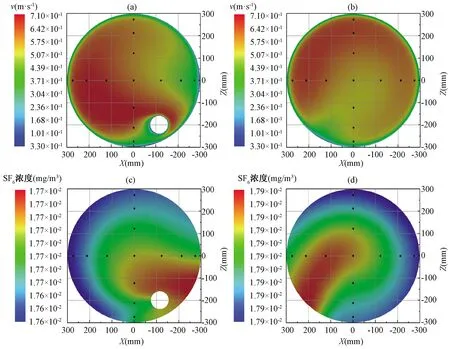
图9 低风速下有无内部管道时速度及SF6分布对比[(a)、(b)：截面速度分布情况，(c)、(d)：SF6浓度分布情况]Fig.9 Comparison of velocity and SF6 distribution under low wind speed [(a), (b): velocity distribution, (c), (d): SF6 concentration distribution]

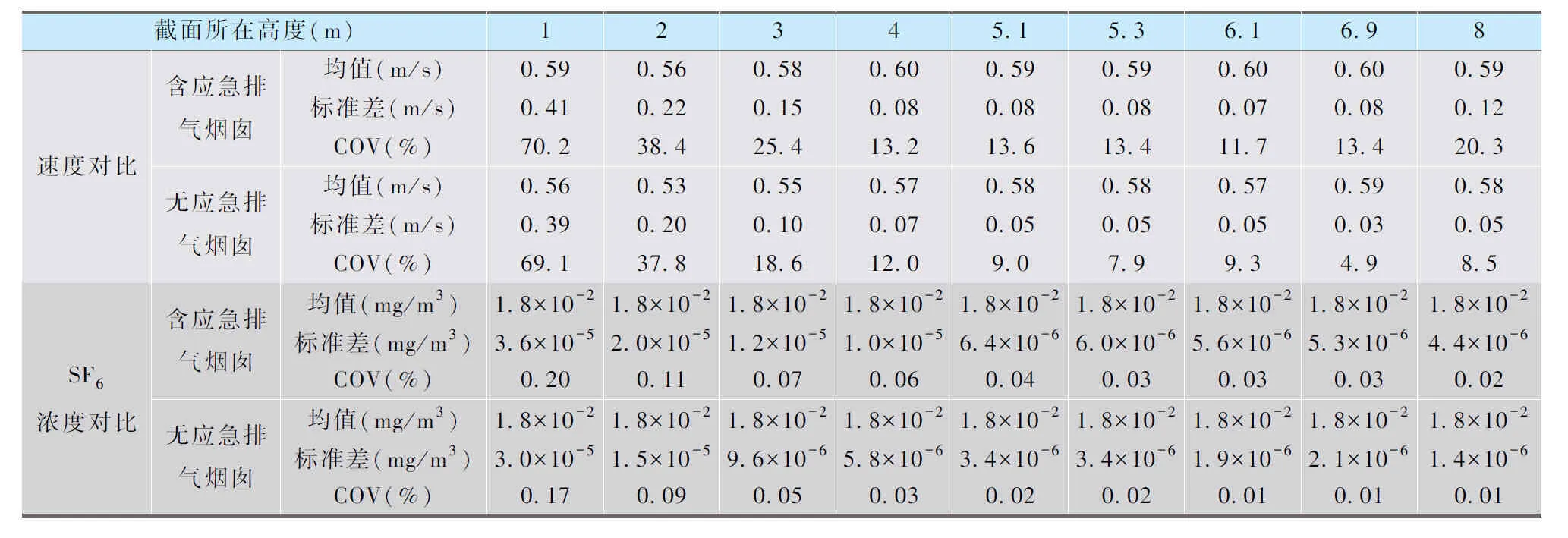
表3 低风速下有无应急排气管道时混合均匀性指标对比Tab.3 Comparison of mixingd uniformity index with or without emergency exhaust pipe under low wind speed

主烟囱平均风速0.56 m/s时，内部流场依然可满足充分的湍流状态。速度和气体组分在无应急排气管道时呈现了更好的混合均匀性，其各截面平均COV相比含应急排气管道的情况分别降低4.8%和0.02%。随着取样截面高度的增加，两模型COV变化曲线走势较为接近，在1 m截面高度处，两模型速度COV值均接近70%，混合均匀性极差。

4 实验结果对比分析

利用现有比例模型实验平台，对内含应急排气管道的烟囱模型进行测量，以检验仿真的可靠性。通过控制风机运行频率获得较为准确的入口边界条件，测量取样监测截面对应位置的风速、示踪气体浓度等数据[3,13]。鉴于实验所获结果有限，采用一系列的计算数据和实验观测数据的符合程度来对CFD仿真性能进行评价较为合适[14]。将三种通风状态下所有监测点位的风速、示踪气体浓度仿真结果(Calculated values)与实验测量值(Experimental values)做商，比较所得值与1的接近程度。仿真与实验结果对比如图10所示。

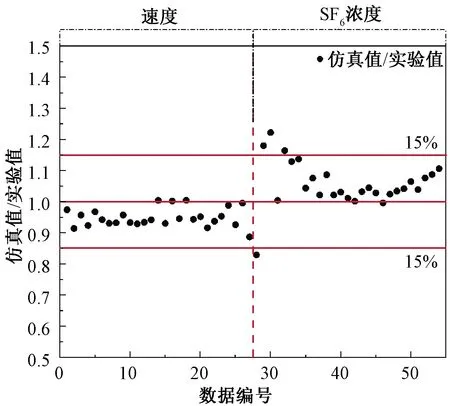
图10 仿真与实验结果对比Fig.10 Comparison of simulation and experimental results

在此定义仿真数据与实验值的偏差为

(7)

式中,xcal为仿真计算值，xexp为实验测量值。经过统计，92.5%以上的仿真数据与实验值偏差低于15%，仿真值/实验值所得全部数据的均值为0.999 89，标准差0.077 12，仿真结果具有较好的可靠性。

对于监测点风速的模拟，计算值相较于实验测定值存在系统性地低估，可能是CFD仿真过程中入口截面平均风速取值偏低所致，而实验中进气端截面中心区域风速高于平均风速；对于监测点示踪气体浓度的模拟，计算值相较于实验测定值存在系统性地高估，原因可能在于CFD仿真过程中风速地低估，而气体注入量取值准确，在取样截面处，示踪气体在空气中的质量浓度被高估，实验中取样截面的气体应更为稀薄。偏差超过15%的数据点为低风速条件近壁点示踪气体浓度仿真值/实验值，偏差原因可能为低风速实验条件下近壁点示踪气浓度不够稳定。并且，CFD方法对于气体流速的预测准确度，优于对示踪气体分布情况的预测，这与CFD方法本身的局限性有关，计算中所考虑的物理过程越复杂，引起的不确定性也越大。通过增加网格数量、更全面的考虑所需物理模型、换用精度更高的求解算法等，可能使偏差进一步降低，此外，使用更为精密的实验设备、增大实验数据量，应该也可提高仿真值与实验值的符合程度[15-16]。