鸟类分类问题数学建模实验研究

彭李嘉

(北京邮电大学 计算机学院，北京 100876)

1 问题的提出

同一片森林里生活着两种鸟，它们外形相似，习性相近。科研人员分别记录了这两种鸟类的翅展(翅膀展开的长度)和身长，如表1所示。

问题一：请根据上述表格，给出一个为这两种鸟类分类的方法。

问题二：现观察到该片丛林中的三只鸟，其翅展和身长的数据分别为(12.50，19.00)(13.00，18.00)(14.00，20.70)。请通过数据进行辨识这三只鸟分别是A类还是B类。

问题三：若科研人员发现记录中有一处错误，翅展13.80 cm、身长19.00 cm的这只鸟应属于A类而非B类，请分析该错误对分类的影响。

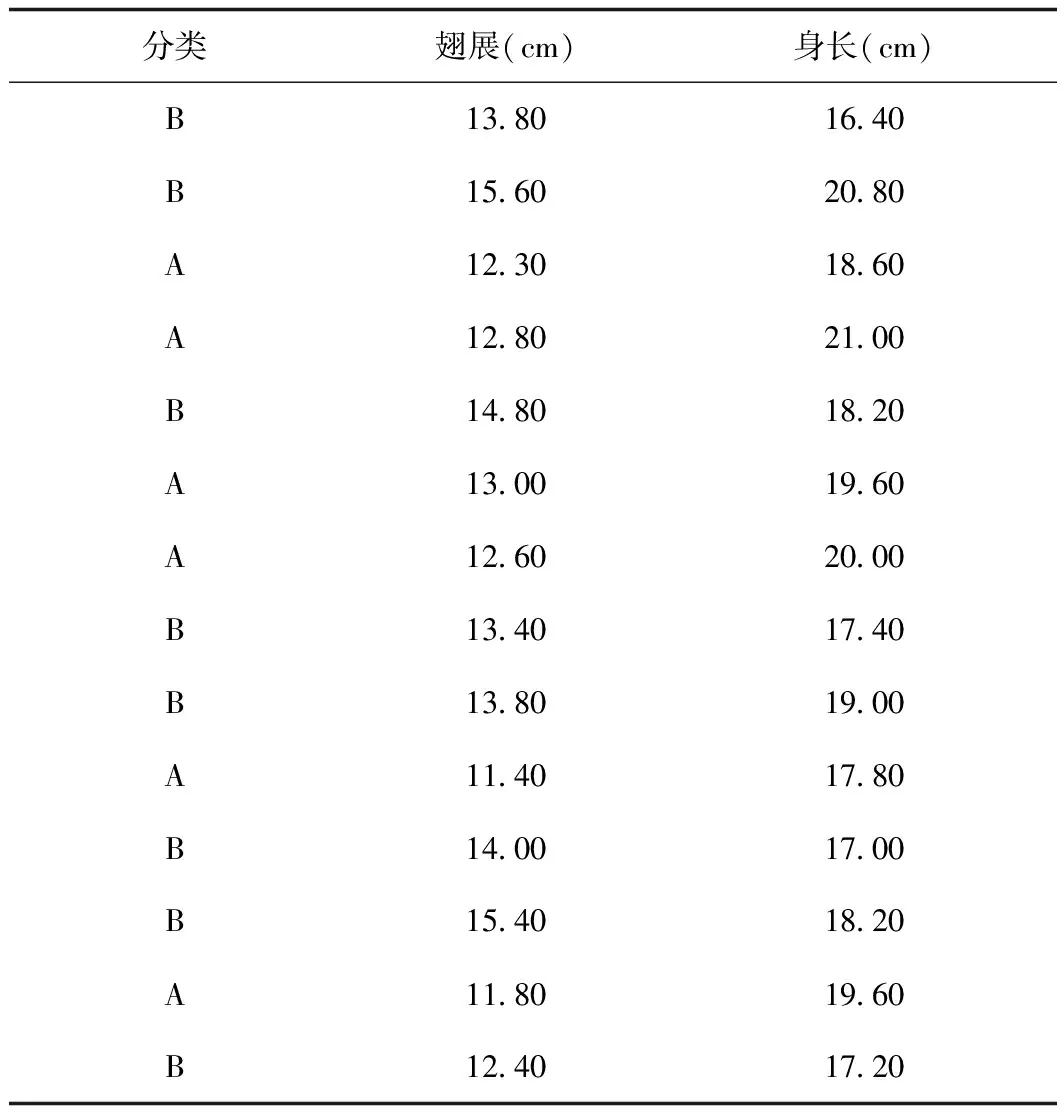
表1 两种鸟类的翅展和身长Tab.1 Wing expanse and body length of two kinds of birds

2 问题分析

对于问题一，题目要求给出为这两种鸟类分类的方法，已知数据是鸟的种类及它们的翅展和身长，因此建立的模型要找到种类与翅展、身长的关系。通过对题目中所给数据的初步分析可以看出：整体特征都是随着翅展长度的增加，鸟的身长也在增加。因此可以认为这两种鸟类的分类与它们的翅展、身长服从一定的规律。但画出散点图之后，自变量之间的关系仍不清晰，因此决定选用逐步分析法找到对因变量有显著影响的自变量，建立模型并运用残差分析法改进模型，给出两种鸟类分类的方法。

对于问题二，题目要求辨识给出的3组数据来确定鸟的分类。问题二的基础是问题一所求得的模型，因此分别将3组数值代入问题一中的回归模型，根据求得种类的值确认该鸟属于哪种类别。

对于问题三，题目要求分析表格中一处错误对分类的影响。问题三的基础同样是问题一，因此在问题一所求得的模型中，将错误数据对应种类的值进行修正，改正后重新建立模型，将新模型所得结果与问题一的结果进行对比，根据两者的差异分析该错误对于分类的影响。

3 模型的假设与符号说明

3.1 模型的假设

假设一：不考虑除翅展、身长之外的其他因素对于分类的影响。

假设二：假设数据中每一只鸟都是纯种鸟，不考虑A、B两种类别鸟的杂交后代及A、B两种类别鸟与其他鸟类的杂交后代。

3.2 符号说明

表2 符号说明Tab.2 Symbol description

4 模型的建立与求解

4.1 问题一的模型建立与求解

4.1.1 问题一的模型建立

将题目中所给的两类鸟数据按照翅展的值从小到大进行排序。

表3 A类鸟翅展值的排序Tab.3 Order of wing expanse value of A type birds

表4 B类鸟翅展值的排序Tab.4 Order of wing expanse value of B type birds

利用matlab软件画出散点图。

a.横轴为翅展，纵轴为身长。

图1 A类鸟散点图Fig.1 Scattered plot of A type birds

图2 B类鸟散点图Fig.2 Scattered plot of B type birds

b.横轴为翅展+身长，纵轴为身长。

图3 A类鸟散点图Fig.3 Scattered plot of A type birds

图4 B类鸟散点图Fig.4 Scattered plot of B type birds

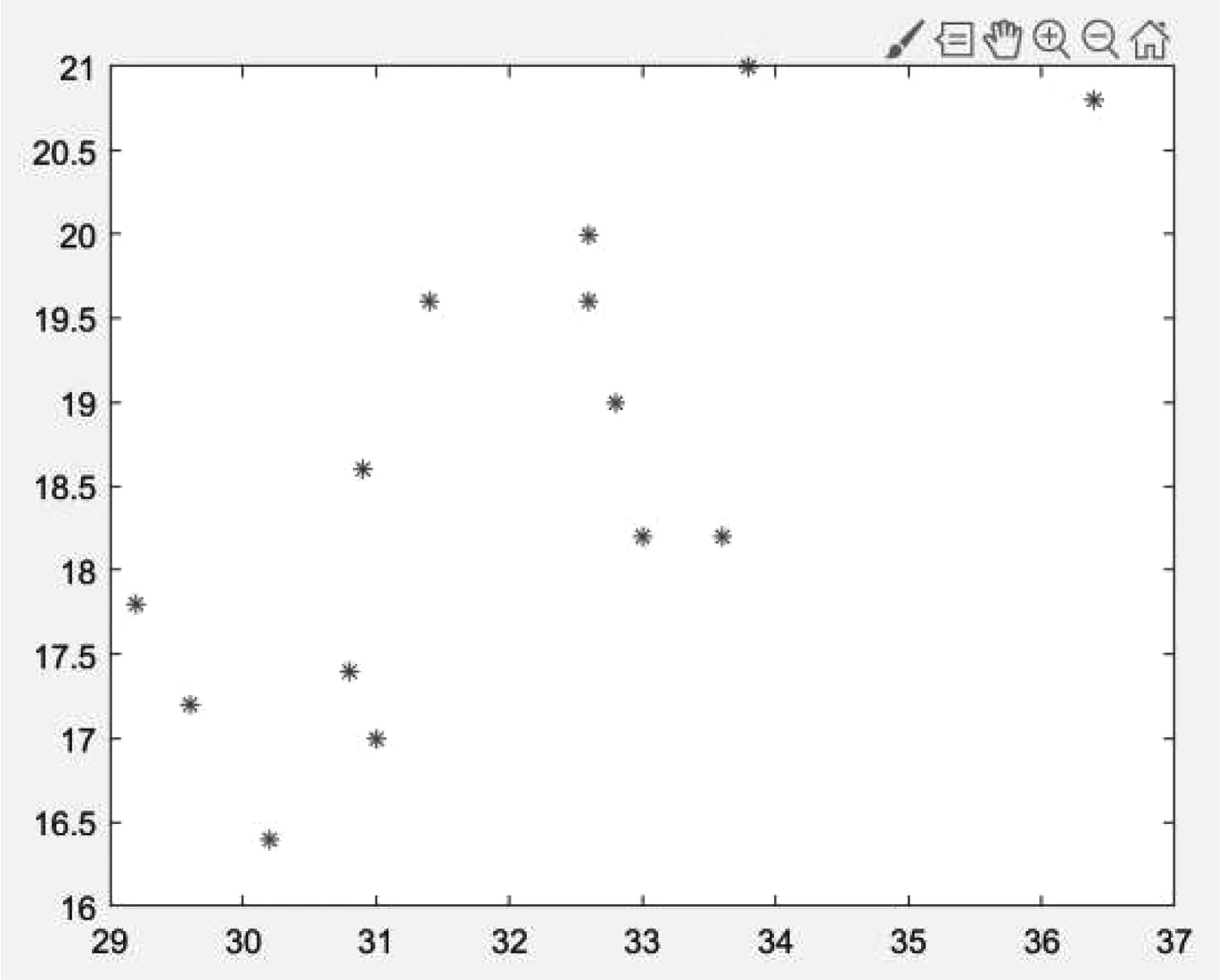
图5 所有鸟类散点图Fig.5 Scattered plot of all birds

c.横轴为翅展*身长，纵轴为身长。

图6 A类鸟散点图Fig.6 Scattered plot of A type birds

图7 B类鸟散点图Fig.7 Scattered plot of B type birds

图8 所有鸟类散点图Fig.8 Scattered plot of all birds

图9 逐步回归图Fig.9 Stepwise regression

因为散点图所反映的关系不明确，因此利用matlab系统工具箱中的逐步回归命令stepwise实现逐步回归[1]。

所加入的自变量：x1=x，x2=x^2，x3=s，x4=h，x5=m，x6=翅展与身长的差，x7=s.*x。其中x2=x^2，x3=s，x4=h，x7=s。

*x加入后，R^2接近于1，F值极大，p接近于0，模型较合适，因此考虑建立翅展的平方项、种类、翅展与身长的和项、种类与翅展的乘积项相关的模型。

利用matlab软件建立模型：y = a + b×s + c×x.^2 + d×h + e×s×x

>> y=[17.80;19.60;18.60;20.00;21.00;19.60;17.20;17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;0;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00;12.40;13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60;29.60;30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(14,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

4.1.2 问题一的模型结果分析

利用excel软件将结果列成表格。

表5 问题一的模型结果Tab.5 Modelling of Problem One

因变量的99.96%可由模型确定，F远超过F检验的临界值，p远小于α=0.05，因此模型从整体上看成立。所有参数的置信区间均不包含零点。

模型结果：y=-7.213 8+1.836 7×s-0.036 0×x^2+1.009 6×h-0.143 8×s×x。

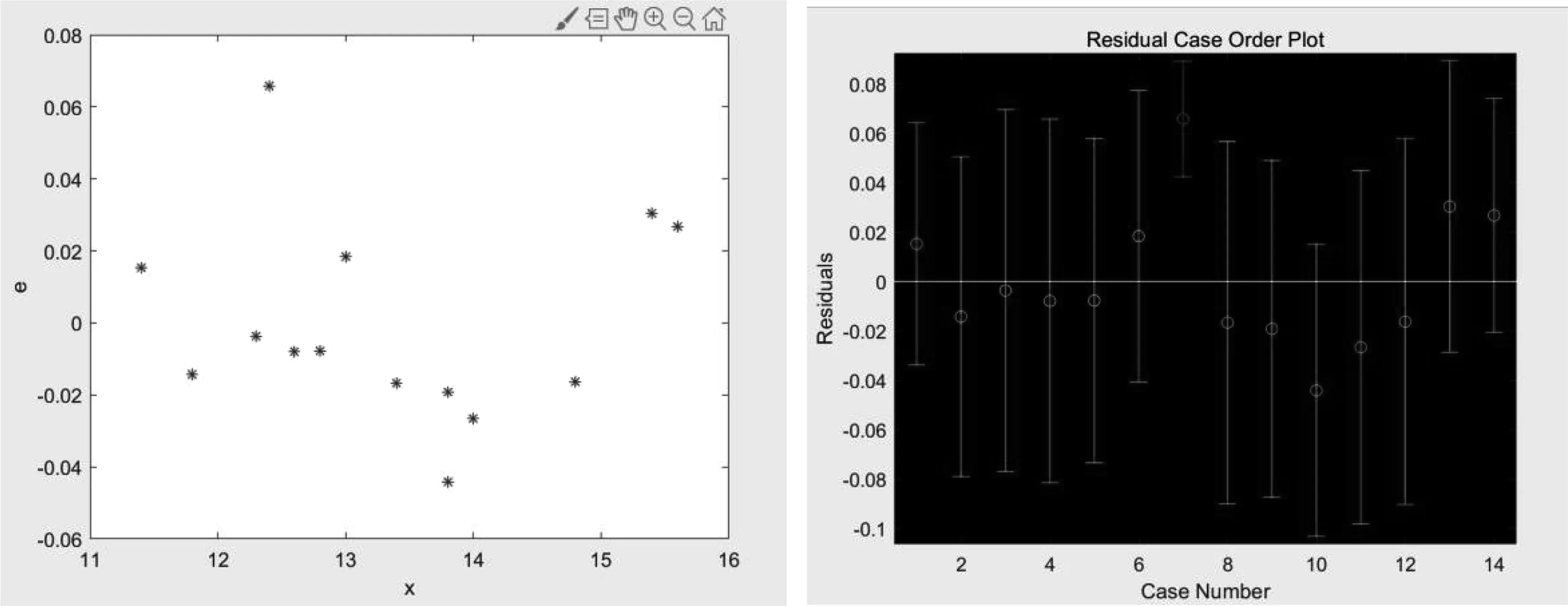
图10 问题一中 X的残差图Fig.10 Residual plot of X in Problem One

4.1.3 问题一的改进模型建立

剔除1个异常数据，利用matlab进行新的回归分析。

>>y=[17.80;19.60;18.60;20.00;21.00;19.60; 17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00; 13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60; 30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(13,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

4.1.4 问题一的改进模型结果分析

利用excel软件将结果列成表格。

表6 问题一的改进模型结果Tab.6 Improved model results of Problem One

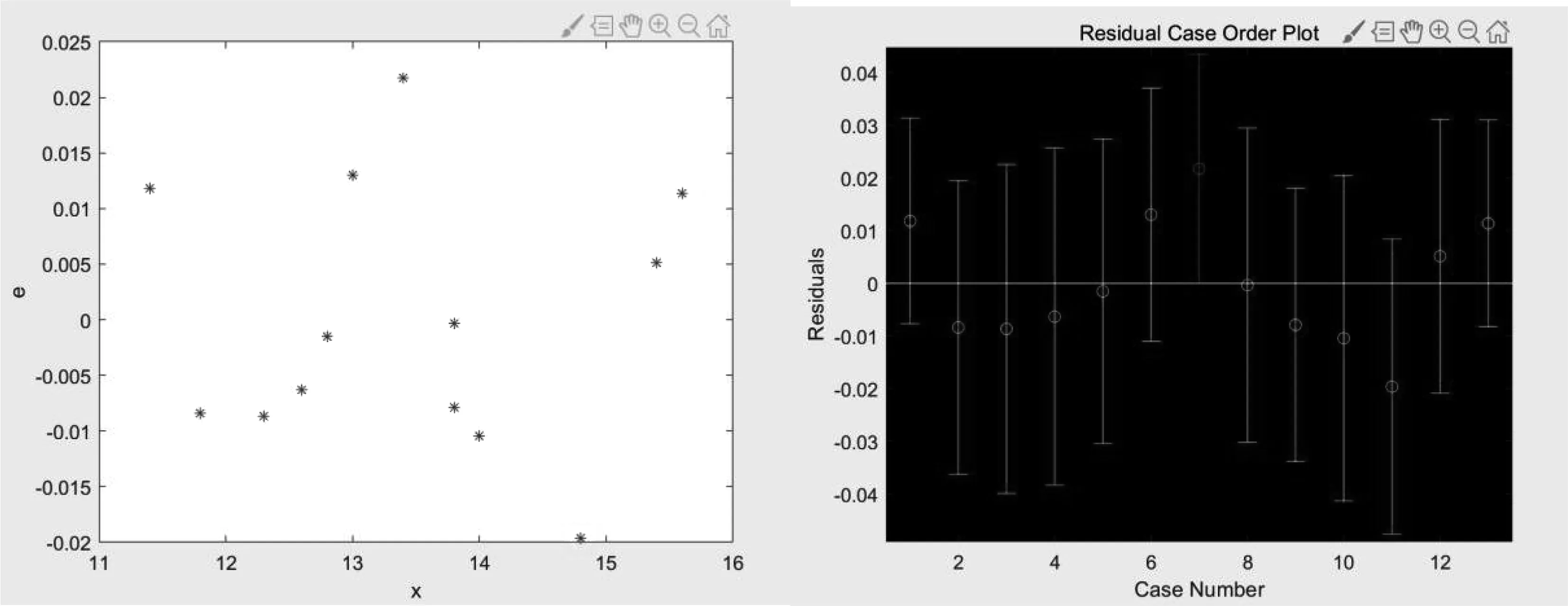
图11 问题一中改进后X的残差图Fig.11 Residual plot of improved X in Problem One

改进后的模型结果：y=-7.302 9+2.161 0×s-0.034 6×x^2+1.002 9×h-0.163 3×s×x。

4.2 问题二求解

将(12.50，19.00)(13.00，18.00)(14.00，20.70)三组数据分别代入问题一中的模型，计算得到s的值，s大于等于0.5，则该鸟属于A类；s小于0.5，则该鸟属于B类。

利用excel列出表格。

表7 三只鸟的归类Tab.7 Classification of three birds

4.3 问题三的模型建立与求解

4.3.1 问题三的模型建立

将(13.80，19.00)这组数据的s值更改为1，重新建立模型。

建立模型：y=a+b×s+c×x.^2+d×h+e×s×x

>>y=[17.80;19.60;18.60;20.00;21.00;19.60;17.20;17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;1;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00;12.40;13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60;29.60;30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(14,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

利用excel软件将结果列成表格。

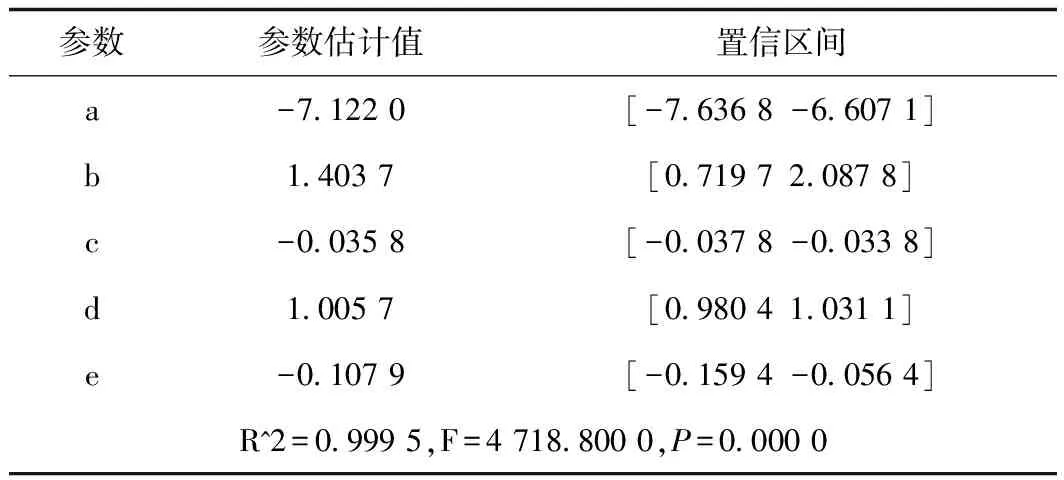
表8 问题三的模型结果Tab.8 Modelling of Problem Three

改正错误后的模型：y=-7.122 0+1.403 7×s-0.035 8×x^2+1.005 7×h-0.107 9×s×x[2]。

图12 问题三中改进后X的残差图Fig.12 Residual plot of improved X in Problem Three

4.3.2 问题三结果分析

利用excel软件将结果列成表格，与问题一所求得的模型数据进行对比。

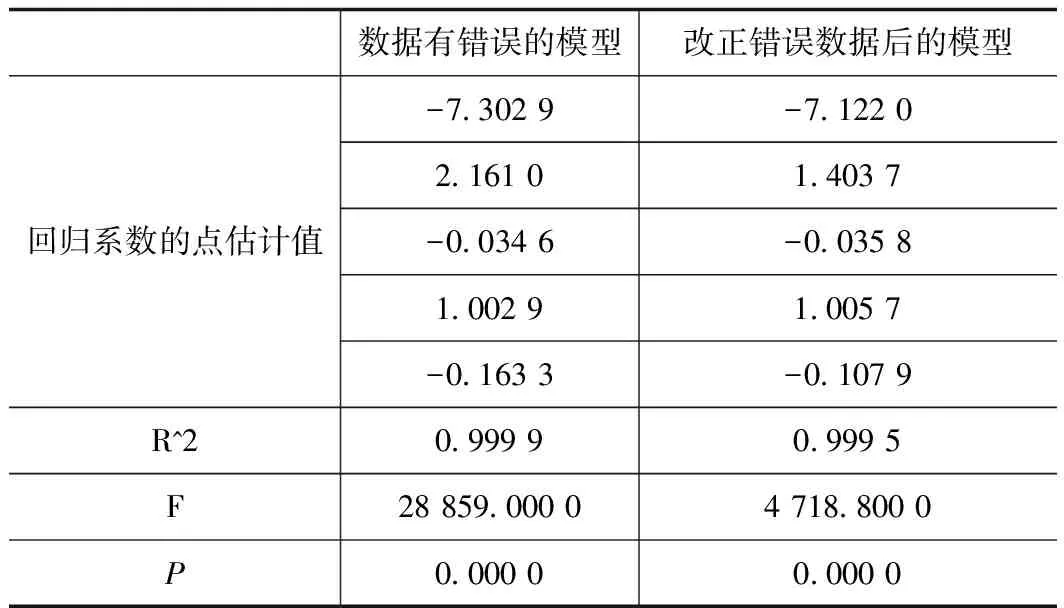
表9 改正错误数据后的模型结果对比Tab.9 Comparison of modelling results after the modification of wrong data

图13 改正错误数据后的前后模型结果对比图Fig.13 Comparison of modelling results before and after the modification of wrong data

与问题一中数据有错误的模型相比，改正错误数据后的模型的常数项较大，种类的系数较小，种类与翅展的积的系数较大，相关系数R^2较小，F值较小。

5 模型分析与改进

5.1 模型的优点

本建模运用逐步回归法研究变量之间的关系，找到对因变量影响较为显著的自变量，以此得到模型；本建模利用残差分析法，将异常数据剔除，改进后的模型的相关系数R^2更接近1，F值更大，使模型得到改进；本建模中所有模型的置信区间均不包含零点[3]。

5.2 模型的缺点

由残差图可以看出，改进后的新模型仍存在异常数据；翅展的二次项的系数极接近于零，对因变量的影响较不显著，应考虑采用其他自变量进行替代。

5.3 模型的改进

本研究只给出了一种改进后的统计回归模型，还有更符合题目要求但未被发现的模型，因此应再给出几种不同的改进模型，进行多角度的比较评价，从而寻找到更优的鸟类分类方案[4]。

6 结论与反思

6.1 结论

针对问题一：利用散点图及逐步回归法找到对因变量有显著影响的自变量，得到鸟类翅展、身长等因素间的关系，建立统计回归模型，并利用残差分析法剔除异常数据以后对建立的模型进行改进。改进后的最终模型是：y=-7.302 9+2.161 0×s-0.034 6×x^2+1.002 9×h-0.163 3×s×x。

针对问题二：在问题一的基础上，将题目中给出的3组数据依次代入问题一所得模型中，根据求得种类的值判断该鸟是哪种鸟类。翅展和身长的数据为(12.50，19.00)的鸟是A类鸟；翅展和身长数据分别为(13.00，18.00)(14.00，20.70)的两只鸟是B类鸟。

针对问题三：将错误数据对应种类的值进行更改，重新建立模型，对比修正后的结果与修正前的结果在回归系数的点估计值、相关系数R^2、F值及与F对应概率p四方面的差异，从而得到该错误对分类的影响大小。改正错误后的新模型是：y=-7.122 0+1.403 7×s-0.035 8×x^2+1.005 7×h-0.107 9×s×x。与问题一中模型相比，改正错误数据后的模型常数项较大，种类系数较小，种类与翅展积的系数较大，相关系数R^2较小，F值较小。

6.2 反思

最开始建立模型时未利用好逐步回归法，常局限于翅展和身长之间的关系，但是发现模型的相关系数R^2只有57.44%，F值也非常小。后建立的模型虽然相关系数等值都较为合适，但总会出现自变量置信区间包含零点的情况。之后，熟悉了逐步回归法和matlab中stepwise命令的用法时，对于自变量的选取有了极大帮助。

刚开始列表格时常用word自带表格，非常不方便，后来利用excel软件可以更加快速简洁地设立表格与图表，使内容表述更加清晰直观。