基于实测资料的京津冀地区地表总辐射最优估算模型研究

张 冉，贾 悦

(河北水利电力学院/遥感与智慧水利创新中心，河北 沧州 061001)

1 研究背景

IPCC第五次会议上明确指出，全球海陆平均温度逐年呈现明显的线性升高趋势，全球变暖现象的发生造成了区域干旱发生频繁，对全球环境造成了十分恶劣的影响[1]。已有研究表明，辐射是影响区域干旱的最主要因素之一，因此探求区域辐射变化规律对区域环境保护政策的制定具有十分重要的意义[2]。同时，现如今发展新能源是国内外相关部门的研究热点，而辐射由于其具有清洁、丰富且可再生的特点，已成为了现如今主要应用的清洁能源之一[3-4]。而获得Rs数据最精确的方法是通过比热计实测获得，但这种方法成本高、耗时高，同时全国752个气象站点中，仅有122个站点可获得实测Rs数据，这极大程度上限制了实测Rs数据的获得[5]。因此，急需找出合适的模型进行估算，高精度高效率获取Rs数据。目前针对的Rs计算方法主要分为经验模型、机器学习模型、辐射传递模型和卫星遥感方法4种[6]。其中，经验模型和机器学习模型由于对气象数据的要求较低和较高的精度，成为了应用最广泛的模型[7]。Rs计算经验模型主要包括温度法和辐射法2大类，Jahani[8]，Chen[9]，邹丽萍[10]等研究人员发现在不同地区，不同方法所表现出的精度不同。自适应性神经网络、M5树模型[11]等机器学习模型均在Rs估算中得到了应用，并取得了一定的进展。

京津冀地区位于我国半干旱地区，属于温带半湿润半干旱季风气候，降水分布不均匀，其所在区域土壤较肥沃，是重要的首都经济圈[12-13]。因此在该区域找出Rs的最优估计方法对当地灌溉决策及防旱制度制定具有十分重要的意义。本文基于3种机器学习模型、3种温度法经验模型和3种辐射法经验模型，以区域实测Rs数据为依据，找出适用于该地区Rs最优估算模型。

2 研究区域与研究方法

2.1 研究区域概况

本文选择区域内均有实测辐射资料的乐亭、天津和北京3个站点，基于站点1994～2017年的实测数据对模型进行训练与模拟，站点分布图可见图1。站点数据均来自国家气象中心，包括实测辐射Rs，风速U2，最高温度Tmax，最低温度Tmin，日照时数n，相对湿度RH，数据质量良好。

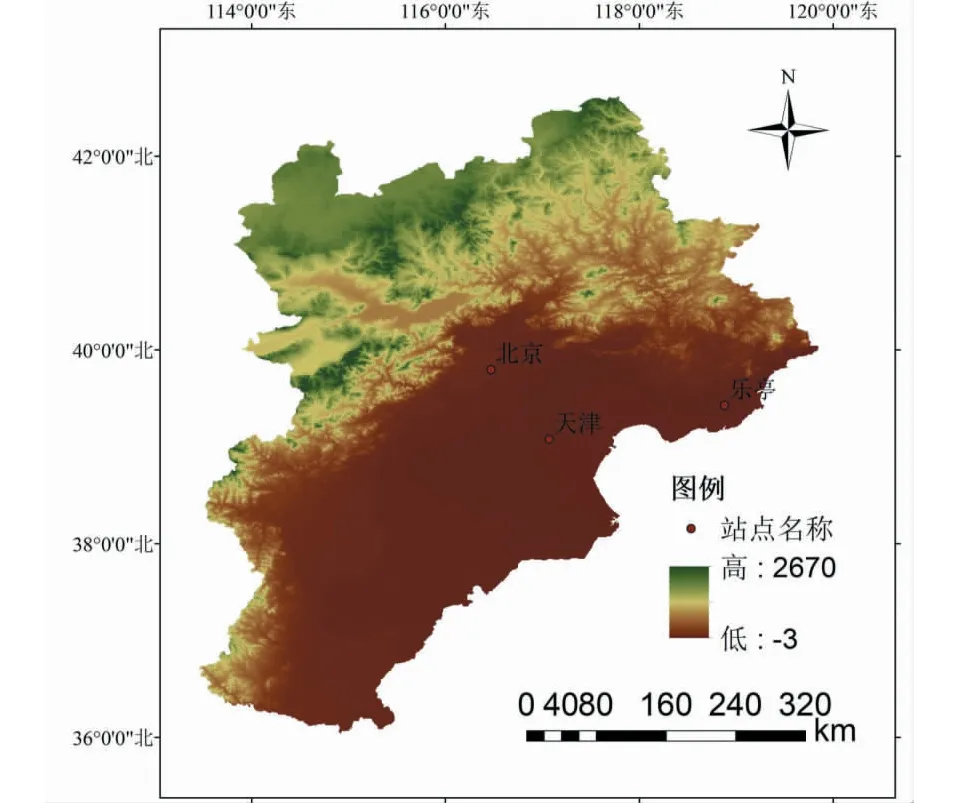
图1 研究区域站点分布图

2.2 辐射法

2.2.1 Angstrom-Prescott模型(AP)

Angstrom[14]通过分析最大日照时数与平均日照时数的关系，提出了AP模型，具体公式如下：

(1)

式中，Rs为总辐射，MJ m-2d-1；Ra为大气顶层辐射，MJ m-2d-1；a，b为常数；n为日照时数，h；N为最大可能日照时数，h。

2.2.2 Ogelman模型(OG)

Ogelman等[15]研究发现了一个二次多项式，可用于模拟Rs，具体公式如下：

(2)

式中参数与上述一致。

2.2.3 Glover-McCulloch模型(GM)

Glover和McCulloch[16]将站点纬度的影响，研究了估算Rs的模型，公式如下：

(3)

式中，φ为纬度取值。

2.3 温度法

2.3.1 Hargreaves-Samani模型(HS)

Hargreaves-Samani[17]模型仅考虑温度即可估算Rs，公式如下：

Rs=[C(Tmax-Tmin))0.5]×Ra

(4)

式中，C为经验系数；Tmax和Tmin分别为最高和最低温度，℃；其余参数与前文一致。

2.3.2 Bristow-Campbell模型(BC)

Bristow and Campbell[18]基于Ra和温度差数据，提出了BC模型，具体公式如下：

Rs=a[1-exp(-bΔTc)]×Ra

(5)

式中，c为常数，△T为温度差，℃，其余参数与前文一致。

2.3.3 Annandale模型(AD)

Annandale等[19]基于HS模型，将海拔与气压层厚度引入模型，得出的AD模型公式如下：

Rs=a[(1+2.7×10-5Z)ΔT0.5]×Ra

(6)

式中，Z为站点海拔高度，m；其余参数与前文一致。

2.4 机器学习模型

2.4.1 极限学习机模型(ELM)

极限学习机模型(ELM)主要可分为输入层、隐含层和输出层3部分，其收敛速度快、精度高，被广泛应用于回归检验中，具体步骤可见文献[20]。

2.4.2 广义回归神经网络模型(GRNN)

广义回归神经网络模型(GRNN)[21]是依据概率最大原则计算网络输出的径向基网络。适于解决各类非线性问题，由输入层、模式层、求和层和输出层等4层神经元组成。

2.4.3 小波神经网络模型(WNN)

小波神经网络模型(WNN)是一种以BP神经网络拓扑结构为基础，将小波基函数作为隐含层节点传递函数，信号向前传播的神经网络，具体形式可见文献[22]。

2.5 评价指标

利用均方根误差(RMSE)、模型效率系数(Ens)和决定系数(R2)分析各模型模拟精度，具体公式如下：

(7)

(8)

(9)

引入GPI指数，比较多个模型多个评价指标的最终精度：

(10)

式中，αj为常数，RMSE取1，Ens和R2取-1；gj为不同指标的缩放值的中位数；yij为不同指标的尺度值。

3 结果与分析

3.1 不同模型Rs日值拟合对比

图2～图4为京津冀地区3个站点不同模型Rs日值拟合对比。由图中可以看出，不同模型对Rs的模拟精度存在一定差异。在机器学习模型中，ELM模型表现出了较高的精度，其模拟值与实测值的拟合方程斜率在3个站点分别为0.873、0.935和0.889，GRNN模型精度次之，WNN模型精度较低；在辐射法中，OG模型精度较高，其模拟值与实测值的拟合方程斜率在3个站点分别为0.911、0.949和0.909，AP模型精度次之，GM模型精度较低；在温度法中，3种模型对Rs日值模拟的精度由高到低依次为BC模型>HS模型>AD模型。综合比较不同模型可知，辐射法和机器学习模型的计算精度要显著高于温度法，其中，OG模型和ELM模型在Rs日值模拟方面表现出了较高的精度。

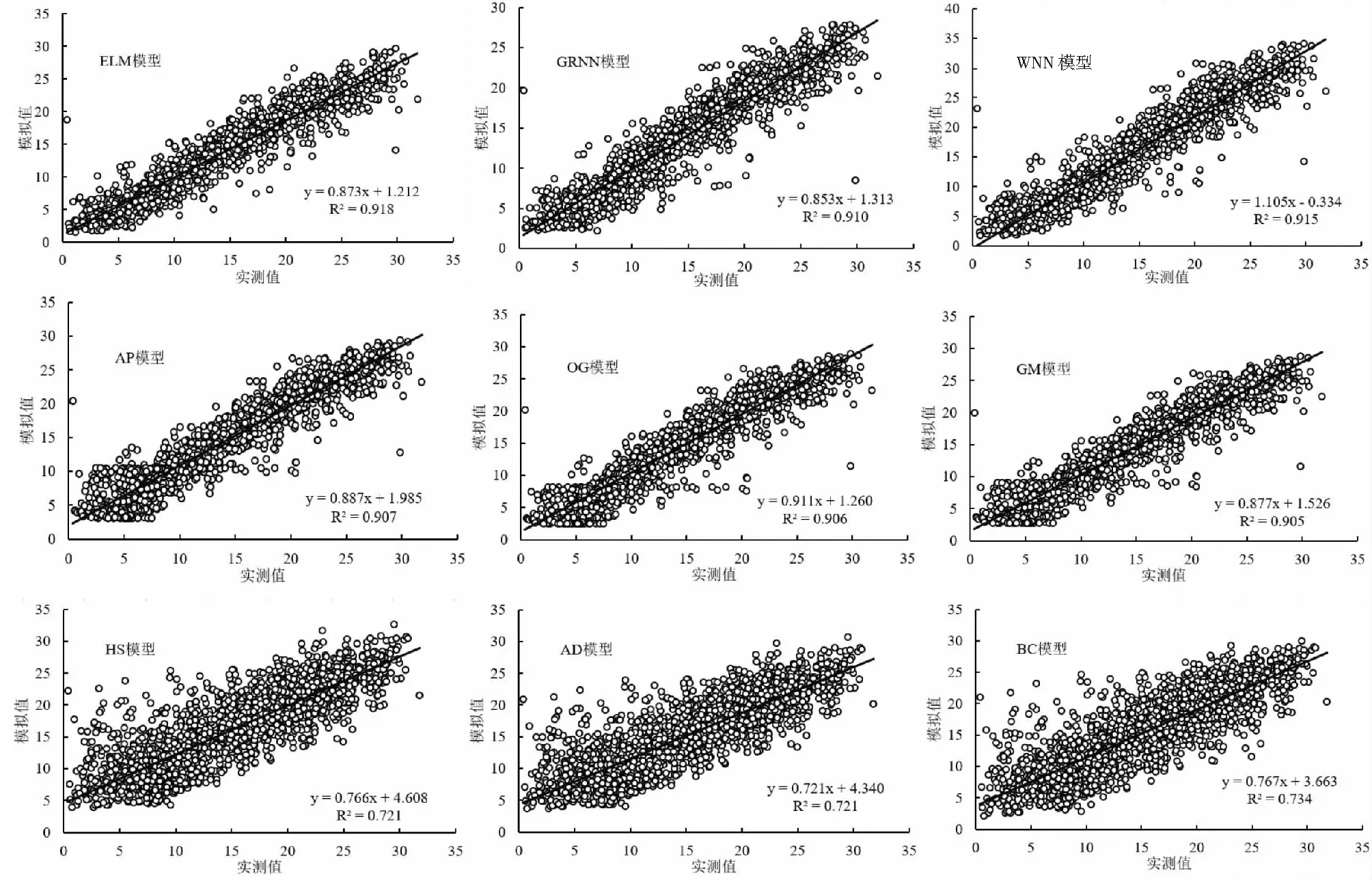
图2 河北乐亭站不同模型Rs模拟拟合图

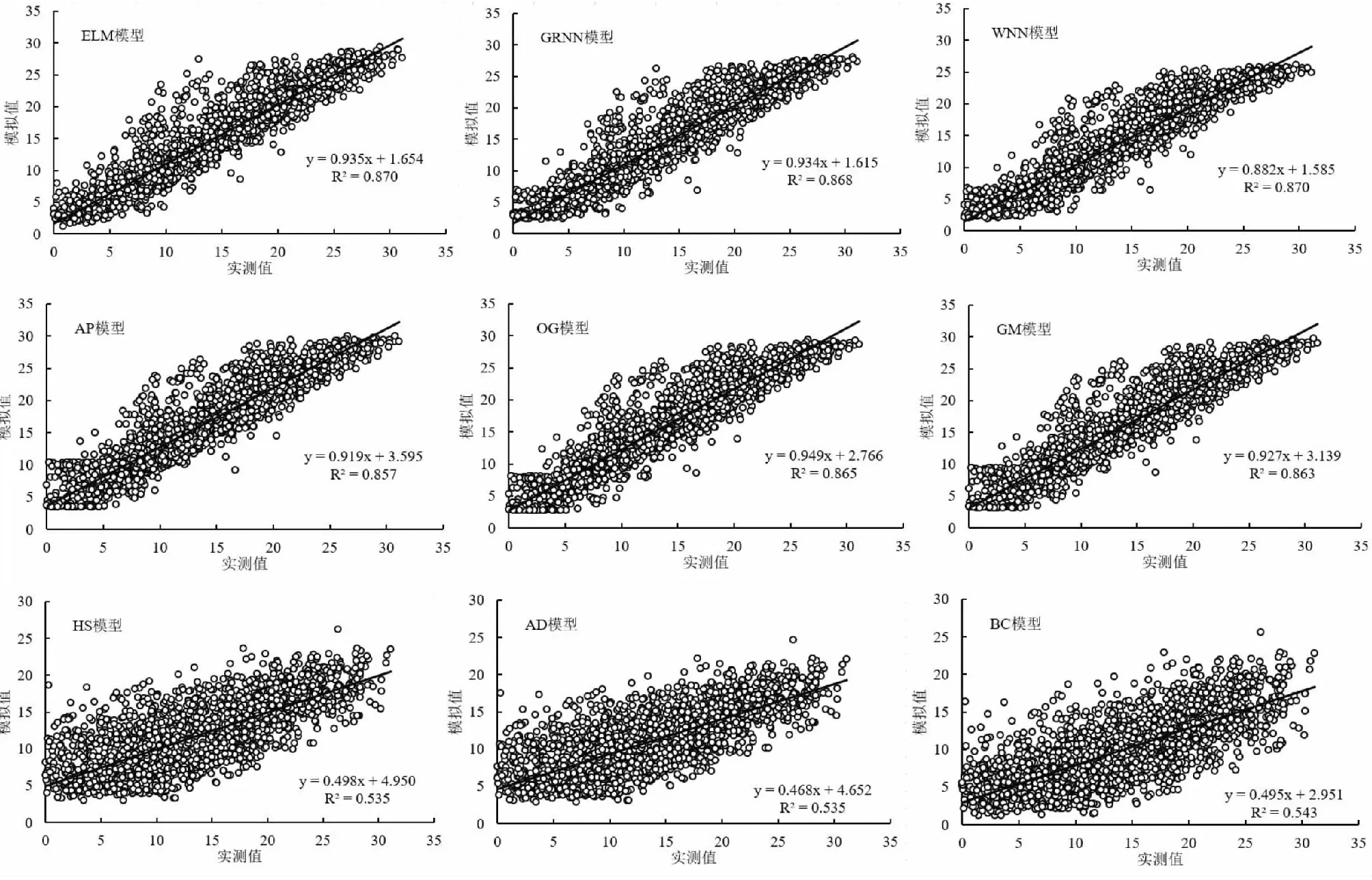
图3 天津站不同模型Rs模拟拟合图

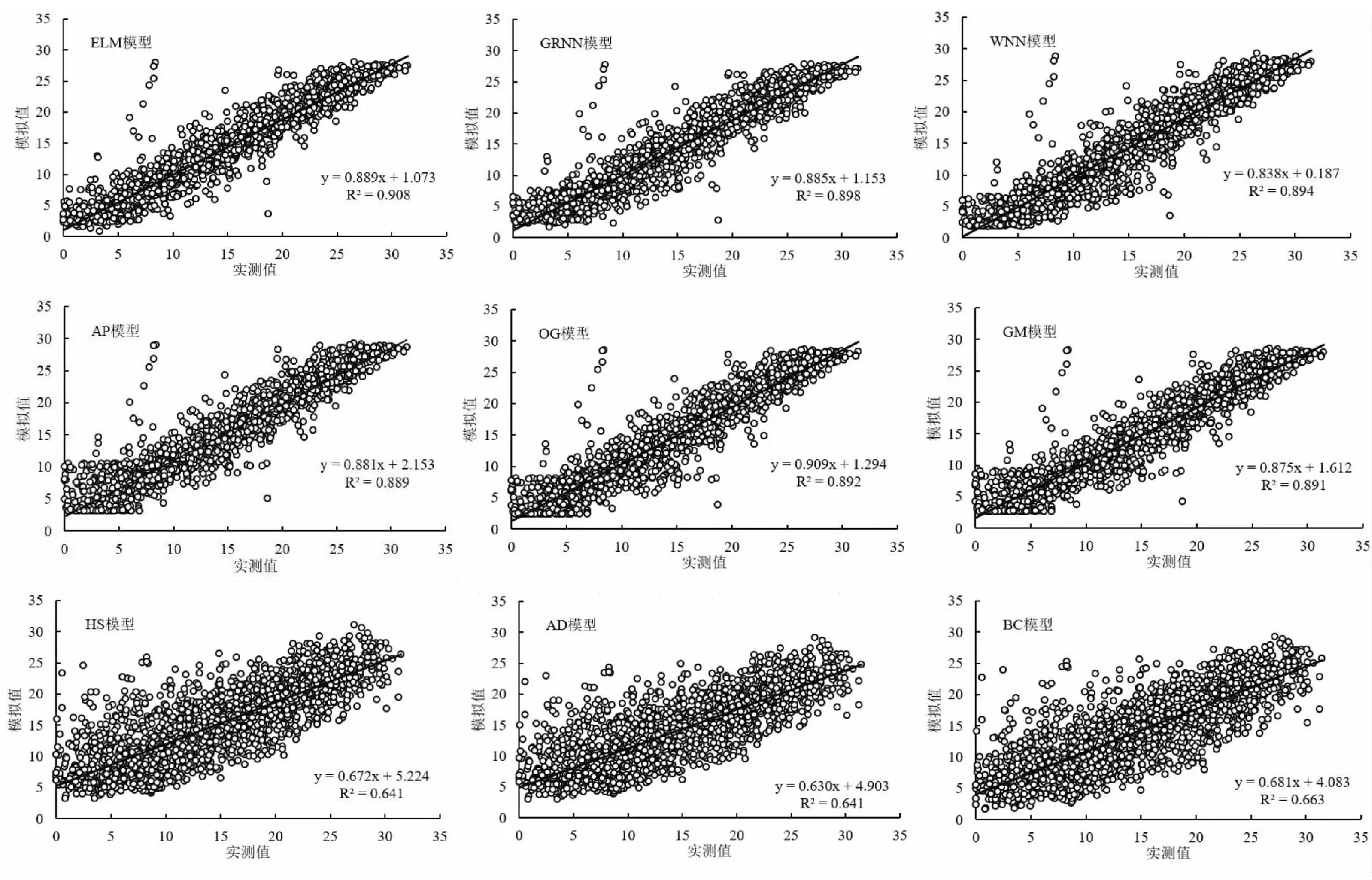
图4 北京站不同模型Rs模拟拟合图

3.2 不同模型Rs月值拟合对比

图5为京津冀地区3个站点不同模型Rs月值拟合对比。由图中可以看出，不同模型对Rs月值的模拟精度存在一定差异，但基本趋势一致，均呈开口向下的二次抛物线型式。不同模型模拟的Rs值在5月份达到最高值，而在12月份取值最低，约80%的Rs均集中在了3～10月的主要作物生长季。对于不同模型，温度法模拟的Rs月值与实测值的变化趋势差异较大，而ELM模型在模拟Rs月值时与实测值的拟合效果最高。

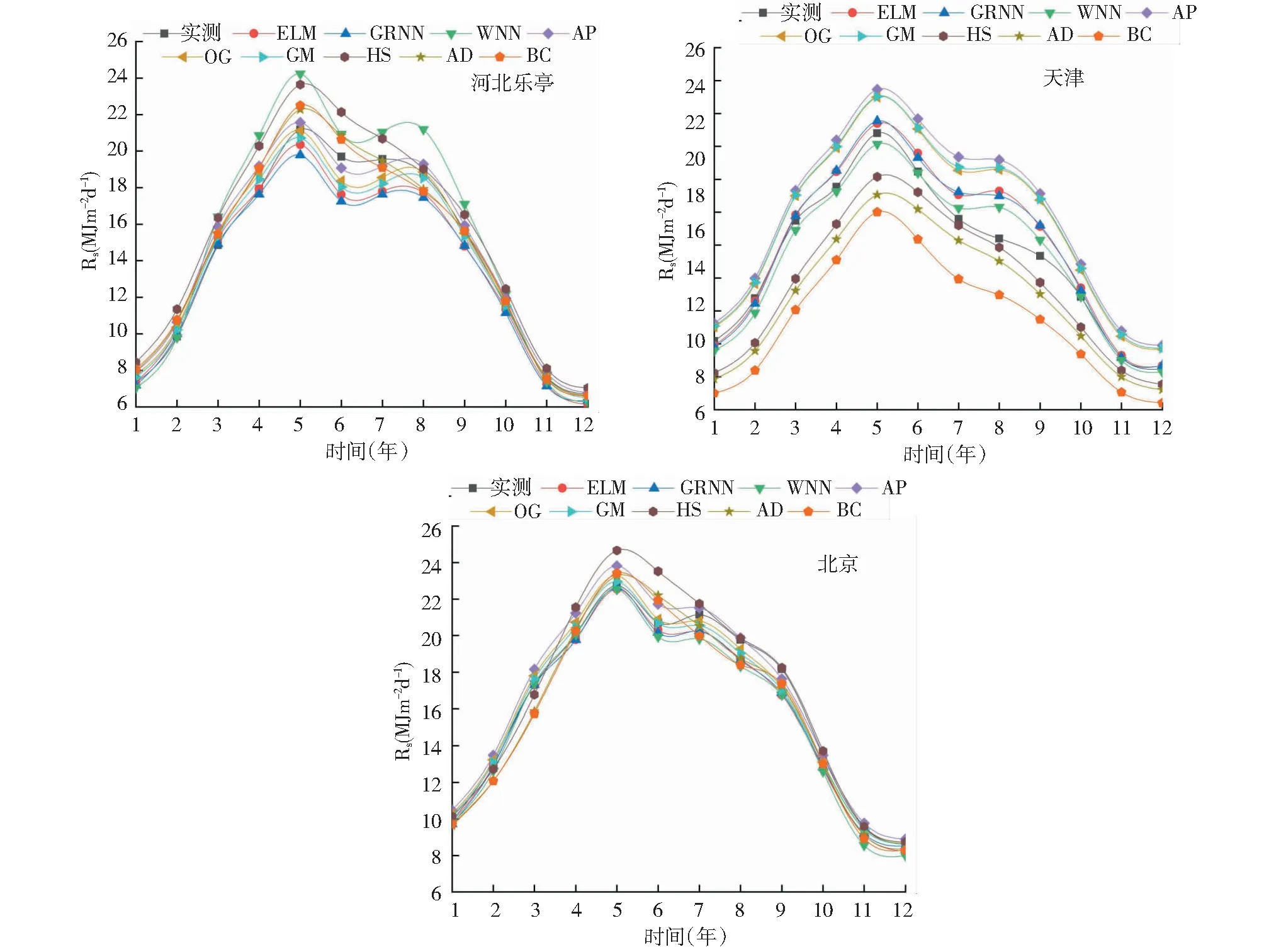
图5 不同模型Rs月值模拟拟合图

3.3 不同模型Rs精度对比

图6为不同模型在不同站点的精度指标计算结果。由图中可以看出，RMSE、R2和Ens组成的评价指标体系可较好地反映不同模型模拟结果的误差与一致性，可较好反映出不同模型的计算精度。其中，3类模型的计算精度表现为机器学习模型>辐射法>温度法，ELM模型计算精度最高，其RMSE为2.393 MJ m-2d-1、R2为0.898，Ens为0.888，GPI为0.192，在辐射法中OG模型计算精度最高，其RMSE、R2、Ens和GPI分别为2.673 MJ m-2d-1、0.887、0.855和0.017，9种模型计算精度由高到低排列依次为ELM模型、OG模型、GRNN模型、WNN模型、GM模型、AP模型、HS模型、AD模型、BC模型。ELM模型克服了传统神经网络模型的缺点，具备学习速度快、泛化能力强、不存在局部极小值和过拟合等问题的优点，这可能是ELM模型在模拟Rs时精度最高的原因。

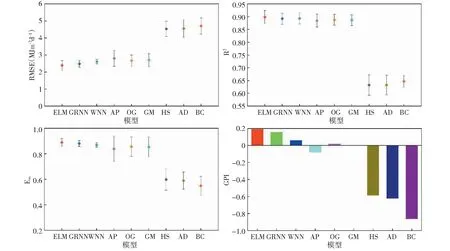
图6 不同模型Rs精度对比

3.4 模型可移植性分析

为进一步证明ELM模型的精度，本文对该模型的可移植性进行了分析。将3个站点任意2个站点作为模型训练数据集，第3个站点作为模型验证数据集，计算了不同情况的模型模拟精度，结果见下表。由表中可以看出，采用不同参数输入集的情况下，ELM模型仍能保持较高的精度，其R2和Ens均在0.88以上，进一步证明了ELM模型计算精度的稳定性。

表 ELM模型可移植性分析

4 结 论

本文基于机器学习模型、辐射法和温度法共9种计算模型，找出了京津冀地区模拟Rs的最优模型，并得出以下结论：

4.1 Rs日值的模拟中的精度较高

在Rs日值的模拟中，ELM模型和OG模型的拟合方程斜率分别为0.873、0.935和0.889，0.911、0.949和0.909，表明这2个模型在京津冀地区Rs日值的模拟中的精度较高；

4.2 在Rs月值的模拟中，ELM模型与实测值的拟合效果最高4.3 ELM模型可作为京津冀地区Rs计算的标准模型使用

通过计算不同模型的精度指标可知，ELM模型RMSE、R2、Ens和GPI分别为2.393 MJ m-2d-1、0.898， 0.888和0.192，计算精度最高，ELM模型可作为京津冀地区Rs计算的标准模型使用。

4.4 ELM模型其计算精度可进一步提高

本文证明了ELM模型在京津冀地区Rs计算的精确性，但由于该模型的权值和隐藏偏差是随机确定的，其计算精度可进一步提高。粒子群算法(PSO)是一种常用的优化算法，在模型优化中已证明了该算法的精度，基于粒子群算法优化的极限学习机模型(PSO-ELM)可进一步提高区域Rs计算的精度，可在今后的研究中进一步讨论。这一有效测量京津冀地区的Rs机械模型的发现将极大的推动未来京津冀地区的Rs的研究进展，为我国太阳能新能源的开发利用直接带来巨大的益处。