AHRS姿态估计的迭代扩展卡尔曼滤波方法
2022-04-28史宜巧
史宜巧,赵 辉
(1.江苏电子信息职业学院智能制造学院,江苏 淮安 223003;2.河北工程大学信息与电气工程学院,河北 邯郸 056038)
1 引言
基于微机电系统(micro−electro mechanical system,MEMS)的惯性测量单元(inertial measurement unit,IMU)和磁罗盘组成的航姿参考系统[1(]Attitude and Heading Reference System,AHRS)通过实时测量到的角速率,加速度,以及磁航向,将短期精度较高(角速率)的姿态计算和长期精度较高(加速度,磁场)的姿态计算结果进行融合,从而实现对载体姿态的估计,在消费级导航,服务型运动感知等低成本要求的领域已经有了广泛的应用[2]。目前常用的AHRS实时姿态估计方法可大致分为互补滤波[3],QUEST型方法[4−5]以及滤波器估计方法[6−8]。其中滤波器方法可以在姿态估计的同时对系统误差参数进行实时估计,且更易于融合各类元件信息以取得更好的整体性能。因此得到了广泛的研究。这里研究即为滤波方法。
在姿态估计问题中应用滤波估计方法需要解决两个问题,一是观测模型通常是非线性的;二是姿态四元数在估计中不能够自然归一化。对此,通常的做法是将过程与观测模型线性化,以四元数等姿态表征参数表示的估计误差和传感器偏差估计误差作为状态量,将加速度计和磁传感器等外部信息作为观测量。将问题转化为线性滤波对状态量进行求解。例如,乘性扩展卡尔曼滤波[9−10(]Multiplicative Extended Kalman Filter,MEKF)将误差四元数作为状态量,利用一阶近似避免了观测信息引入的非线性,且隐式地包含了归一化条件。由于截断误差的影响,基于误差估计的方法估计精度不高,尤其在姿态变化剧烈条件下可能产生较大的误差。
针对上述问题,这里将姿态变量与传感器偏差参数直接作为待求解状态,提出一种基于非线性滤波的四元数姿态估计算法。根据四元数姿态表示原理和传感器测量输出模型建立了AHRS 系统四元数姿态估计的直接形式非线性状态空间模型,采用构造伪观测量方法解决四元数归一化问题,在此基础上推导出了观测函数的雅克比矩阵,采用迭代扩展卡尔曼滤波(iter‐ated EKF,IEKF)方法进行滤波求解,实现了对姿态的实时估计。此外,利用阈值法处理载体机动时产生的运动加速度。通过实际传感器测量与ABB 机器人同步姿态参考数据集对这里算法进行了验证,并与基于非线性滤波、互补滤波等的姿态估计方法以及商用姿态测量单元的结果进行了对比。结果表明,相比现有常用方法,这里算法在姿态估计准确度与精度方面具有较好的性能。
2 四元数姿态估计的非线性问题模型
设载体自身坐标系(B系)为右-前-上坐标系,参考系(N系)为东-北-天局部导航坐标系(ENU)。姿态四元数定义为:
式中:ψ=|ψ|,且ψ=ψμ;
μ—N系中的转轴矢量;
ψ—从系通过转轴转到系所经过的角度。
因此可以得到从B系变换到N系的姿态变换矩阵为:
在ENU坐标系下可得上式姿态变换矩阵对应的欧拉角为:

式中:Rij—矩阵(q)相应位置的元素。
根据式(2)给出的变换关系,下面推导四元数姿态估计的非线性状态空间模型。
2.1 状态方程
考虑到待求解的量和影响姿态估计精度的因素,将四元数,陀螺仪偏差βω,加速度计偏差βa以及磁传感器偏差βm作为状态量,即:

根据各个状态量随着时间的动态变化过程,下面来导出状态方程,四元数随时间变化的动态方程为:

式中:=ω−βω;ω—陀螺仪读数;
βω—陀螺仪偏差;
υω~N(0,Σω)—陀螺仪测量噪声,矩阵:

各个传感器偏差视为一阶Gauss−Markov过程,即:

式中:系数矩阵Αi,i=ω,a,m—对角矩阵,对角元素分别为三轴分量对应的Gauss−Markov过程系数;ηi~N(0,)为相应的过程噪声。
对式(5)和式(7)进行离散化,可得离散状态方程为:

上式中状态转移矩阵A与过程噪声vk分别为:

其中,

假设过程噪声均值为0,则过程噪声协方差矩阵为:

对角上的协方差矩阵分别为:
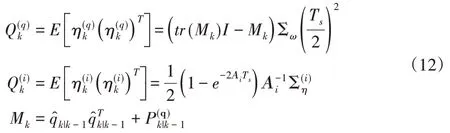
2.2 观测模型
以静止条件下加速度计和磁传感器的输出ak,mk为观测值。各个传感器的输出模型可写为参考系中的自然矢量到体坐标系的变换加上测量误差。

g—当地重力加速度;
根据式(13)可进一步构建观测模型为:

3 基于迭代扩展卡尔曼滤波的姿态估计算法
在上一节建立状态-空间模型的基础上,现在可以直接利用IEKF算法对姿态四元数及各个传感器的偏差进行估计,IEKF算法在目标跟踪领域已经比较成熟,其原理和推导过程可见文献[11−12]。在此仅给出算法关键步骤。
(1)时间更新
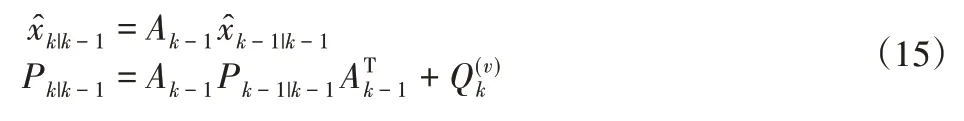
(2)观测更新

当迭代至设定次数M或状态值稳定时,令
在观测更新过程中,由于载体本身机动,会产生较大幅值的运动加速度,这一方面会降低测得加速度中包含的姿态信息量,使得姿态估计误差增大,另一方面会与式(13)给出的观测模型是不相符的,可能导致滤波器发散。这里采用对观测值进行阈值判别的方法来改善,即采用如下判别准则来确定是否进行下一次迭代:

式中:g—重力加速度;
ai,i=x,y,z—加速度计的测量值。
若满足上式,则认为当前的加速度观测值可以用于观测更新,否则不进行观测更新。
对于观测方程中的磁传感器测量模型,当地地磁参考矢量一般需要通过全球地磁模型计算获得,为避免对于外部数据的依赖,这里中采用构造磁参考量的方法,即在式(13)中用近似值bN替代bN。

当前估计得到的磁传感器零偏误差。
根据上述过程可以得到基于IEKF 的姿态估计算法步骤如下:
(2)根据上一时刻状态估计值和基于式(11)和式(12)计算出的过程噪声协方差矩阵,利用(15)计算当前状态预测值和相应的协方差矩阵Pk|k−1。
(3)若当前加速度计的观测值满足式(17),则利用前述的IEKF观测更新步骤计算,Pk|(k计算过程中利用式(18)构造磁参考量);若不满足,否则回到步骤(2)。
(4)对当前状态估计值中的四元数部分进行归一化。回到步骤(2)或算法结束。
4 结果与分析
本小节基于一个开放的姿态测量数据集[13−15]来验证这里方法的有效性,同时给出常用的互补滤波姿态估计方法对该数据集的处理结果和误差情况作为性能对比。该数据集中包括几种常用低成本惯性测量单元原始数据、商用级姿态传感器姿态输出结果以及ABB公司工业机器人给出的姿态四元数。各个传感器输出数据均是以ABB机器人为平台,在与之固联的条件下同步测量得到。因此,工业机器人输出的姿态四元数可以作为真实姿态参考。此外,采用同样与ABB机器人固联同步测量的两型商用高精度姿态单元Xsens MTi−30和PNI SENTRAL M&M给出的姿态估计结果作为对比。
这里方法和其他几种姿态估计算法的输入均采用数据集中包含的Inversense 公司MPU9150 型IMU 测量数据,除集成有MEMS加速度计和陀螺仪外,该型IMU还包括了一个磁罗盘(三轴磁强计)。测量数据包括IMU与机器人固联转动时MPU9150传感器测得的三轴加速度、三轴角速度与三轴磁场数据。IMU与ABB机器人固联转动的轨迹与姿态,如图1所示。机器人转动速度为0.3m/s。

图1 IMU与ABB机器人固联转动轨迹与姿态Fig.1 Trajectory and Orientation of ABB Robot Borne IMUs
MPU9150测得的三轴加速度,三轴角速度,三轴磁场等原始数据,如图2所示。图中显然可见转动过程中的数次机动在传感器测量结果导致了不同程度的瞬态变化。基于该组数据,采用这里方法与Madgwick互补滤波算法进行对姿态四元数进行估计求解。

图2 MPU9150原始数据(转动速度0.3m/s)Fig.2 Raw Data from MPU9150(Spinning Sspeed 0.3m/s)
为了直观地比较姿态估计准确性,利用式将各个算法估计及机器人给出的参考四元数转换为欧拉角。这里算法与Madgwick互补滤波算法得到的欧拉角,MTi−30 给出的欧拉角以及PNI SENTRAL M&M给出的欧拉角与机器人运动过程中的参考姿态的对比情况,如图3~图6所示。(图中:roll—横滚角;pitch—俯仰角;yaw—偏航角,下文同)

图3 这里算法姿态估计vs.参考姿态Fig.3 Proposed vs.Referenced

图6 PNI SENTRAL M&M传感器姿态估计vs.参考姿态Fig.6 Orientation Estimates:PNI SENTRAL M&M vs.Referenced
从图中可见,相比各个算法及姿态测量单元给出的结果,根据这里算法计算出的欧拉角与机器人得到的欧拉角整体上最为接近,且在机动情况下的姿态跟踪响应要优于其他方法给出的结果,同时可见两型姿态传感器在机动时均出现了较大的姿态误差。
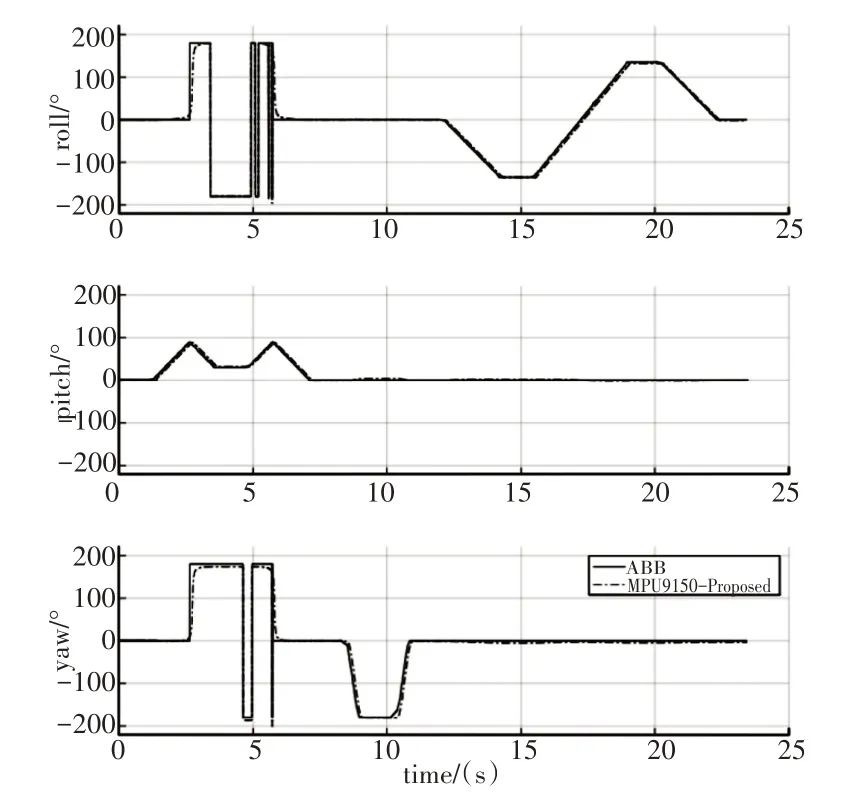
图4 Madgwick算法姿态估计vs.参考姿态Fig.4 Orientation Estimates:Madgwick vs.Referenced
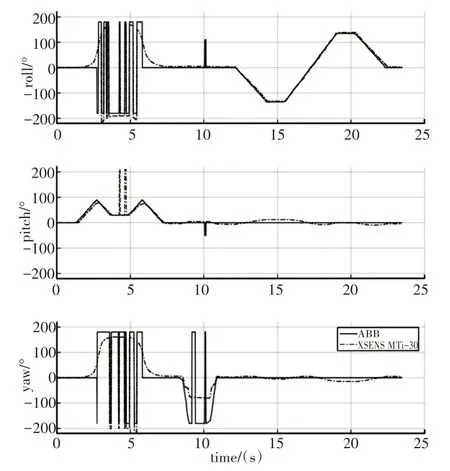
图5 XSENS MTi−30传感器姿态估计vs.参考姿态Fig.5 Orientation Estimates:MTi−30 vs.Referenced
根据上述两种算法估计结果和两型姿态传感器输入结果,通过下式进行计算时间平均的均方根误差(RMSE)。
式中:T—测量时间;
γkk时刻的(任一)欧拉角的参考值和估计值。

进一步地,依据式(19)给出了各个方法所得欧拉角的(时间)均方根误差,如图7所示。图中显然可见这里算法的误差最小,这表明这里算法的姿态估计结果与ABB机器人给出参考姿态在时间均方意义上最为接近;围绕均方根误差值的标准差,如图8所示。可见这里方法估计误差在整体上的波动最小。

图7 各个方法所得欧拉角的均方根误差Fig.7 Root Mean Square Error of Euler Angle by Each Method

图8 各个方法所得欧拉角误差围绕均方根误差的标准差Fig.8 Std.of Euler Angle Centered by RMSE for Each Method
5 总结
这里针对低成本AHRS系统姿态估计准确性不足问题提出一种基于非线性滤波求解的姿态估计方法。通过构建基于直接形式姿态估计的非线性状态空间模型采用迭代扩展卡尔曼滤波方法实现了对姿态四元数与传感器偏差的实时估计。通过实测数据对这里算法进行了验证。结果表明,这里算法在姿态估计准确性与估计精度上优于现有常用姿态估计方法。下一步需要针对如何从算法优化和模型改进上进一步提高基于直接形式非线性姿态估计方法的计算效率等方面展开研究。
