自润滑关节轴承轴向游隙润滑油流量计算方法
2022-04-28徐东华吴悦明王永祥苏一丹
徐东华,吴悦明,王永祥,苏一丹
(1.广州航海学院实验中心,广东 广州 510725;2.广东工业大学机电工程学院,广东 广州 510120;3.广州航海学院船舶与海洋工程学院,广东 广州 510725)
1 引言
自润滑关节轴承是机械工程领域最重要的基础元件,其性能对设施全局能效具有深刻影响。轴向游隙是轴承的关键质量指标,影响轴承旋转准确性与定位精度,是其使用寿命与效能的评测参考指标[1]。轴向游隙不断朝着高转速、重载荷方向发展,对其内部管路润滑需求越来越高。若某些管路润滑油流量无法实现设计要求,不能供应足够的润滑油,致使零部件摩擦发热,对轴承稳定运行造成极大威胁[2]。因此着重研究润滑油的流量分配问题。
自润滑关节轴承的自润滑衬垫摩擦性优良,在轴承运行时生成的摩擦力很小,可确保轴承工作精度。文献[3]利用变温航空润滑油流量标准装置,对10支涡轮流量计在多个粘度点下实施校准试验,对各粘度下流量计仪表系数完成数据解析。以涡轮流量计理论模型为前提,提出以双指数衰减函数对仪表系数采取拟合计算。文献[4]将微涡轮和微电容组合测井仪置于井筒截面不同高度处,同步测量局部流体速度和持水率,采用持水率插值成像算法确定局部流体性质和油水分界面高度,将局部流体速度的涡轮测量值与数值模拟计算值相结合,建立过流截面速度场分布最优化计算模型,实现水平井油水两相分层流分相流量测量。
上述方法流量计算条件约束较多,无法完成轴向游隙润滑油流量计算目标。通过分析自润滑关节轴承原理,明确轴向游隙内部管路数值,利用伯努利方程推算流体与阻力与压力,完成高效准确的流量计算。
2 轴向游隙值确定
自润滑关节轴承在工作时,轴承外圈内侧的自润滑衬垫在载荷与转速带动下,在内圈金属表面构成一层很薄的软材料表面膜。因其剪切强度小,黏着点在膜内实施滑动剪切,把轴承内外圈的相互摩擦变换成自润滑固体润滑剂分子之间的摩擦,此种变换模式大幅降低了摩擦力[5]。
把自润滑关节轴承依照不同衬垫材质实施划分,主要分成下列三类:双金属自润滑关节轴承、复合材料自润滑轴承和固体镶嵌自润滑关节轴承。复合材料自润滑关节轴承的自润滑衬垫通常使用二硫化钼、碳纤维等材料,在某种精度需求高的工业控制水准下,为了让轴承拥有更优质的自润滑特征[6],也可把轴承外圈采用自润滑材料进行组装。
把自润滑关节轴承根据外圈的不同架构实施分组,分为如下四类:双半外圈关节轴承、单缝关节轴承、双缝外圈关节轴承及整体关节轴承。前三种类型因为架构上拥有缺口,会极大影响轴承负载能力,约束了轴承工作精度的同时,也降低了轴承使用年限,此种架构的关节轴承不能在高精度需求状态下进行真实应用。整体外圈型自润滑关节轴承没有上述缺陷,可以保障轴承的应用寿命与精度。
自润滑关节轴承的游隙表示轴承套圈沿径向或轴向通过某个极限位置往另一相对极限位置移动的大小,分为径向游隙与轴向游隙,制造者与应用者大多根据轴向游隙创造及选择轴承。轴承应用者通常会误以为轴承只要有游隙就会对精确度造成影响,这实际上是没有区分游隙与精度间的相互关联[7]。游隙是确保轴承寿命、降低摩擦、振动与噪音的必要条件。同时,游隙的选择对轴承工作精度具有相当程度的影响,关键是怎样按照轴承的真实工作条件去明确恰当游隙。
若轴承外圈对应于内圈上下浮动,获得轴承轴向为:

式中:G1—外圈上极限位置抵达内圈的距离,单位为:cm;G2—下极限位置抵达内圈的距离,单位为:cm;由此可以看出,测量轴承轴向游隙仅需固定一个圈,另一个圈也会上下移动,这样就能测量游隙内部管路值。
在自润滑关节轴承设计与使用过程中,通常根据轴承的安装应用环节与状态,把轴向游隙划分成初始游隙、安装游隙与工作游隙。影响轴承安装游隙的关键元素是轴颈、座孔及轴承间的过盈配合会致使游隙降低,将该影响元素记作δA,影响轴承工作游隙的关键元素有轴承温度改变、旋转离心力等。假设轴承温度改变致使的游隙变化量是δT,三个类型游隙间的关联解析式为:

式中:初始游隙uro—轴承成品合套游隙;安装游隙urA—轴承安装在轴颈与轴承座孔后的游隙;工作游隙urF—轴承位于平稳运行情况下的游隙。
轴承制造者明确游隙的流程,从实际上讲,就是运用式(2)在考虑轴承一般装配条件与正常工作温度范围前提下,逆向求解出最优初始游隙,给应用这供应恰当的轴承部件。针对轴承应用者,采用式(2),按照轴承的详细工作条件去挑选合理的初始游隙,并进行合理过盈配合,确保自润滑关节轴承在运作中具备最优的工作游隙。
轴承的内外圈依次和轴颈、外壳孔以过盈配合连接在一起,过盈配合在配合面位置会产生装配应力。针对不同类型的轴承,其不同形态的轴向截面可等效当作等截面积矩形,把内外圈当作后壁圆筒。
通常轴承内圈旋转时,其应力与形变不光受到装配应力影响,还遭受离心力影响[8−9]。把内圈看作旋转圆盘,将其位移微方程记作:

式中:ρ—密度,单位为:g/cm³;μ—游隙,单位为:cm;ω—角速率,单位为:弧度每秒;E—弹性模量;r—过盈量。按照弹性定理,求出在外压作用下,外圈内管路的轴向变形量是:

式中:R2—轴向半径,单位为:mm。若内外圈温度逐步上升,滚动体直径变大,导致游隙减少,滚动体直径改变量是:

式中:T1和T2—滚动体工作温升时间的均值,单位为:min。
3 基于伯努利方程的轴向游隙润滑油流量计算方法
为了给轴向游隙内部管理供应足够的润滑油,提升其工作性能,降低摩擦系数,设计基于伯努利方程的轴向游隙润滑油流量计算方法。
根据滚动体直径改变量计算可得到轴向游隙值,但是润滑油不是无法压缩的理想流体,因此,在仅考虑重力状况下,按照欧拉方程求解定常流动流体单一流线的伯努利方程[10],记作:

式中:g—重力加速度,单位为:m/s2;zi—流线方位的比位能;pi—流线方位的流体压强,单位为:Pa;vi—流线位置的流体流动速率,单位为:bps。
按照流能量守恒定律,若流体黏性生成的质点摩擦和质点因为惯性碰撞引发的运动速率变化,致使产生流动阻力情况下,流体动能就会降低,单位时间以内管路出口位置的流量变小。所以要精确算出流体阻力与压力损失,获得轴向游隙管路内流体真实流量。
3.1 流动阻力
单一流线的伯努利方程证明:在相等流线上每个点的单位质量流体的总比能是常数。
按照流体润滑有关机理,z1、z2是流线上随机点比位能,p(ρg)代表流线上随机点比压能,v( 2g)是流线内随机点比动能。针对黏性润滑油流体而言,因为抑制黏性阻力影响会损耗机械效能,让流体下游的机械效能低于上游机械效能,得到:

式中:α1、α2—动能修正指数;vˉ1、vˉ2—流速均值,单位为:mm/s;hw—流体经过两个截面时,单位质量流体通过阻力引发的能量损耗,单位为:J;hw由缓变流流动的全部阻力损耗∑hf与局部阻力损耗∑hj共同构成。按照上述公式,单位质量流体沿程阻力损耗是:

式中:l—轴向游隙管道长度,单位为:mm;d—管道直径,单位为:mm;λ—沿程阻力指数。
单位质量流体的局部阻力损耗是:

式中:ζ—局部损耗指数。
3.2 流动压力
流体压力润滑,是凭借被润滑的一对固体摩擦面之间的相互运动,让处于固体之间的润滑流体膜内生成压力,承担外载荷避免固体互相碰触,具有降低阻力和维护固体表面的功能。构成流动压力要符合如下条件:两个固体表面之间具备楔形孔空隙,空隙内拥有黏性流体,且流体可以吸收在固体表面,固体表面相互运动就是润滑流体从空隙大的端点向小空隙端点的运动。
流动压力公式为:

式中:ψ—对应空隙;Ω—轴承转动速率,单位为:r/min;μ—润滑油动力黏度,单位为:Pa·s。为评估每次迭代计算结果能否满足精度需求,明确能否停止迭代流程,针对常规性问题,明确了方程组模式、边界条件与收敛定理后,就能算出正确的流体压力值。
3.3 轴向游隙润滑油流量计算实现
无法压缩黏性流体在轴向游隙管内流动过程中,若雷诺数小于2000情况下,就会产生管路内的层流流动。设定游隙管内是定常流动,同时管中的流速只有沿半径r向有变化,沿x方向没有变化,拓展定常管内流动,顺着x方向圆柱体受到的净力是0,得到:

式中:τ—流层剪切应力;Δp—压降损耗。
压缩润滑油流体在游隙圆管内层流动过程中,抑制黏性阻力生成的压降损耗是:

最终利用线性归纳法,构建一个润滑油流量计算的二次线性函数,求得最终结果即为最优流量分配模式。
4 仿真实例
为验证上述步骤的准确性,将自润滑关节轴承应用在工程机械变速箱上,工程机械变速箱运转工作状况复杂,输入转速的变化范围较广,实施润滑油流量计算时,要充分考虑转速流量计算特征。以自润滑关节轴承在发生耦合故障问题时,其转子结构的裂纹相对深度为0.5mm为例,其裂纹的刚度系数应当在两个转动周期内幅值应当以波浪型的趋势发生改变,幅值波动较大的长周期和幅值波动较小的短周期。
根据自润滑关节轴承的转动形式,假设发生耦合故障问题时,轴承转子裂纹位于主动轮转轴位置,假设裂纹的单元长度L为75mm,裂纹单元的直径d为25mm,轴向游隙输入转速通常是(900~2100)r/min,转速范围大,这也导致润滑油流量产生巨大变化,自润滑关节轴承轴向游隙润滑节点,如图2所示。润滑节点和支路标号均已在图中标出,其中支路开关12−14,15−17,18−20分别为联络开关,初始状态下均处于断开状态。自润滑关节轴承轴向游隙润滑接入5个沿程阻力损耗hf,hf接入位置选择重要等级高的负荷节点和系统末端。

图1 自润滑关节轴承轴向游隙润滑节点设置Fig.1 Setting of Axial Clearance Lubrication Node of Self Lubricating Spherical Plain Bearing
依据上述节点设置,采用所设计方法分析不同转速下轴向游隙管路内每个主要润滑点的润滑流量计算特征,如图2所示。
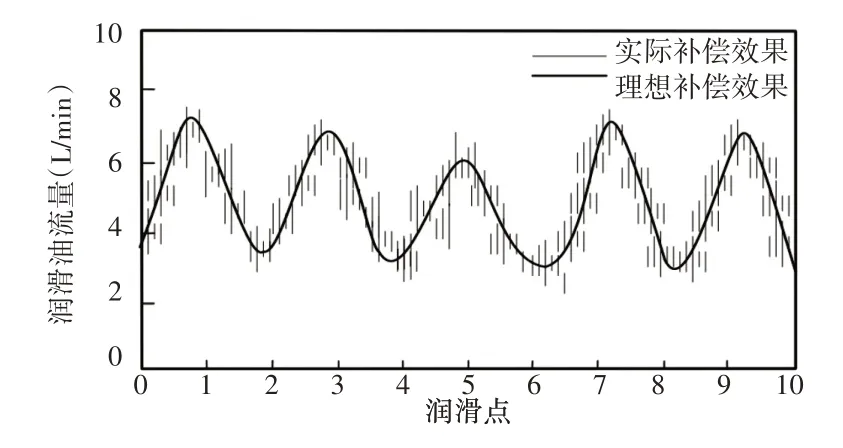
图2 所设计方法润滑油流量计算特征Fig.2 Calculation Characteristics of Lubricating Oil Flow in this Method
从图2可知,润滑点流量大小发生变化,实际补偿效果与理想中补偿效果趋于一致,在理想补偿效果上下驱动,流量分配比例基本相同,证明所设计流量计算方法具有很高的稳定性,适用于多种不同的部件组装,可用性强。
为证明所设计方法流量计算效率,将文献[3]和文献[4]作为对比方法,对三种方法进行润滑油流量计算效率对比,实验次数为8次,结果,如表1所示。

表1 三种方法运算效率对比Tab.1 Comparison of Operation Efficiency of Three Methods
从表1可知,所设计方法计算时间显著低于两种文献方法,耗时均值为3.91s,其中文献[3]方法运算耗时最长,均值为5.66s,文献[4]次之,均值为5.10s。
文献[3]方法由于流量计算点过多,导致其运算时间较长。文献[4]中的持水率插值成像算法推算流体界面高度时,会产生多个解,对正确解的筛选消耗大量时间。
在自润滑关节轴承轴向游隙自然润滑换流下,获取润滑油流量动态规划的谐振回路模型,在等效约束参数控制下得到游隙润滑油流量输出偏差,如图3所示。

图3 游隙润滑油流量输出偏差结果Fig.3 Output Deviation Results of Clearance Lubricating Oil Flow
由图3可知,采用所设计方法的游隙润滑油流量节点输出偏差较小,输出偏差值在0.2上下浮动,所设计方法利用伯努利方程算出单位质量流体的总比能,为计算流体阻力与压力提供有效参考,提升了算法整体计算效率,保证自润滑关节轴承及时运转,以及自润滑关节轴承轴向游隙润滑油流量计算的准确性。
5 结论
(1)所设计方法分析不同转速下轴向游隙管路内每个主要润滑点的润滑流量计算特征,实际补偿效果与理想中补偿效果趋于一致;
(2)所设计方法运算时间短,耗时均值为3.91s,计算精度高、速度快;
(3)采用所设计方法的游隙润滑油流量节点输出偏差较小,输出偏差值在0.2上下浮动,可及时有效降低轴向游隙摩擦力,提升自润滑关节轴承全局性能,为机械工程的持续发展提供充足保障。
