考虑材料物性热效应热障涂层活塞热特性研究
2022-04-28郭东东龚京风郑安文
郭东东,龚京风,郑安文
(武汉科技大学汽车与交通工程学院,湖北 武汉 430081)
1 引言
为减少内燃机热损失提高热效率,目前采用的主要方式是在高温部件表面制备陶瓷涂层(也称热障涂层)进行热防护、减少热损失。热障涂层(Thermal Barrier Coating,TBC)具有高隔热性、高耐热性、高热效率、低排放性等优点[1]。TBC能有效阻隔热量传向基体,但使活塞头部温度梯度增大,涂层与涂层、涂层与基体之间热膨胀系数的不匹配容易形成热应力问题,从而导致涂层早期失效。为揭示TBC对活塞热特性的影响机理,国内外科研工作者对TBC活塞热特性进行了多方面的研究,一般都是把TBC活塞材料的物性热效应处理成常物性进行分析,这样就忽略了材料物性热效应对TBC活塞的影响。由于材料的物性随温度的变化而变化,绝大多数在高温环境下发生剧烈波动,因此用常物性代替材料的物性热效应显然不符合材料的热特性规律,将直接影响问题分析的准确性。因此分析考虑材料物性热效应的TBC活塞的热特性就尤为必要。
文献[2−5]分析TBC厚度对活塞温度场和热应力的影响,指出涂覆TBC可以改善活塞的受力分布。文献[6−7]指出活塞顶部应力以热应力为主,温度对活塞的应力起主导作用。文献[8−9]研究常物性参数TBC活塞的热应力,指出陶瓷层阻隔了大部分热量,活塞应力主要受周向应力影响。目前关于TBC活塞热力性能的研究相对较少,主要集中在TBC的结构、类型和厚度方面,缺乏考虑材料物性热效应对活塞热特性的影响。通过分析采用热固耦合的方法研究TBC活塞材料物性热效应对温度场和热应力的影响。
采用有限元方法,建立TBC 活塞热固耦合模型。将计算得到的活塞顶面温度和应力曲线与已研究成果对比,验证分析方法的正确性。
根据不同温度下物性参数值得到材料物性随温度变化的拟合函数,用于分析材料物性热效应对活塞温度场和热应力的影响,为TBC活塞结构设计、材料选择提供参考。
2 活塞计算模型
2.1 活塞有限元模型
以某柴油机活塞为研究对象,活塞直径为170mm。由于活塞几何模型、约束条件、热边界条件近似对称,取活塞模型的1/4作为研究对象。涂层采用双层型TBC,粘结层厚度为0.2mm,陶瓷顶层厚度0.8mm。采用自由四面体网格对模型分区域剖分。由于TBC厚度较薄,为提高计算精度,对TBC网格进行细化处理,最大单元为6mm,最小单元为1.1mm,单元数为125584,如图1所示。

图1 活塞网格模型Fig.1 Meshes Model of Piston
2.2 模型验证
为验证所用数值方法的正确性,数值模拟TBC活塞的温度场和热应力。结果表明活塞表面沿轴θ=45°的温度和应力值与CV−FVM[10]计算结果基本吻合,如图2、图3所示。验证所用方法的正确性,可用于考虑材料物性热效应的TBC活塞热固耦合热特性研究。
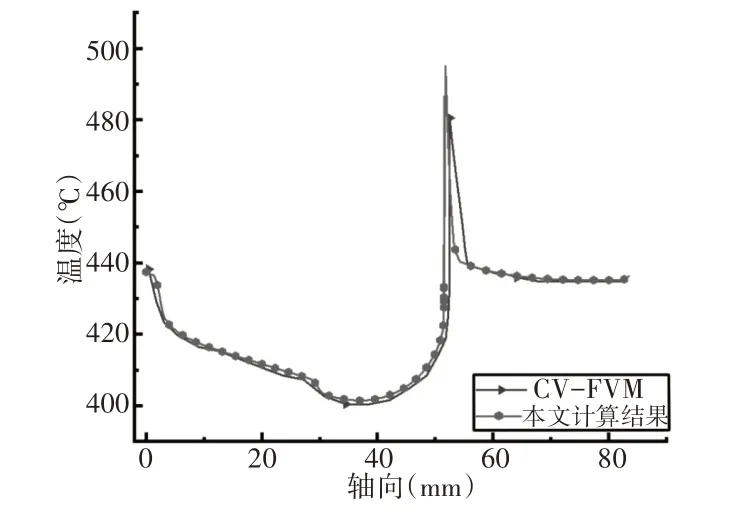
图2 活塞表面表θ=45°线上温度对比Fig.2 Temperature Comparison of Piston Surface θ=45°

图3 活塞表面θ=45°面线上应力对比Fig.3 Stress Comparison of Piston Surface θ=45°
3 材料物性参数
通过查阅《中国材料工程大典》和参考文献[11],确定材料的物性参数有比热容、导热系数、杨氏模量、膨胀系数等,如表1所示。TBC活塞基体材料为Ni−alloy,粘结层为NiCoCrAlY,陶瓷顶层为ZrO2。对TBC活塞的陶瓷层、粘结层和基体物性进行分块定义。把材料物性热效应随温度变化的关系拟合成温度的函数,嵌入有限元分析软件中的材料属性明细列表中,使材料的物性热效应随温度的变化而变化,确保求解的物性热效应参数与温度场相匹配。
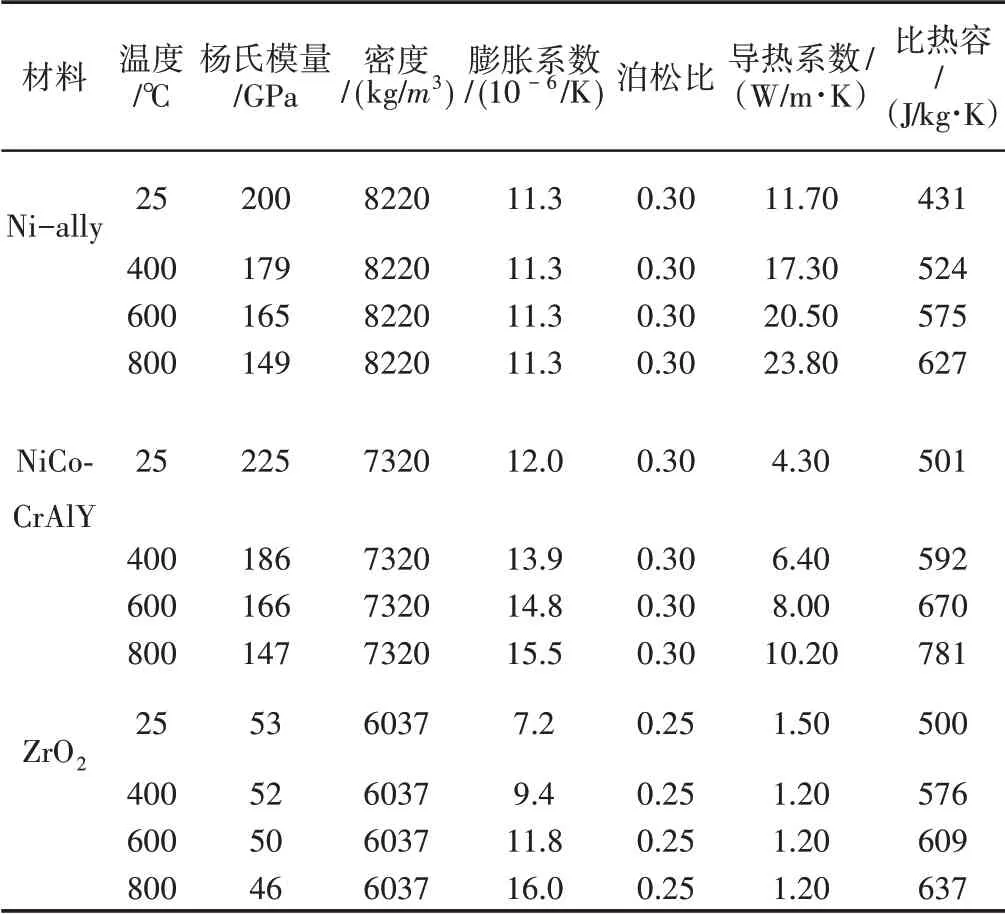
表1 材料物性参数Tab.1 Property Parameters of Materials
4 边界条件的确定
4.1 导热控制方程
无内热源,稳态导热方程为:

式中:T—温度;k—导热系数。
传热采用第三类边界条件,即规定物体与流体表面传热系数和环境温度,表达式为:

式中:λ—导热系数,W/(m∙k);h—对流换热系数,W/(m2∙k);tf—环境温度,K;tw—固体壁面温度,K。
4.2 活塞侧面边界条件
活塞侧面的换热系数比较复杂,研究难度较大,因此将此部分近似处理成多层平板传热系统。其环区换热系数k0计算公式:

火力岸的传热系数k1计算公式为:

裙部的换热系数k2计算公式为:

式中:αℎ—冷却水与缸壁换热系数,W/(m2∙k);a—气缸与活塞环区的间隙,m;b—缸套厚度,m;c—活塞环槽上侧面与环的上侧面的间隙,m;λ3、λ2、λ1—活塞环导热系数、缸壁导热系数、燃气的导热系数,W/(m∙k);a0、a1—气缸与火力岸、裙部的间隙,m;λ0—冷却机油的导热系数,W/(m∙k)。
4.3 燃气侧边界条件
高温燃气与活塞顶直接接触,燃烧室的燃烧过程较复杂,边界条件较难获得。因此利用GT−Power软件对发动机额定工况下实际运行过程进行模拟,GT−Power计算模型主要包括燃油供给系统、进排气系统、燃烧模型等,模拟得到的缸内燃气瞬时压力和缸内燃气瞬时温度与实验值基本一致,如图4、图5所示。验证仿真计算的正确性。
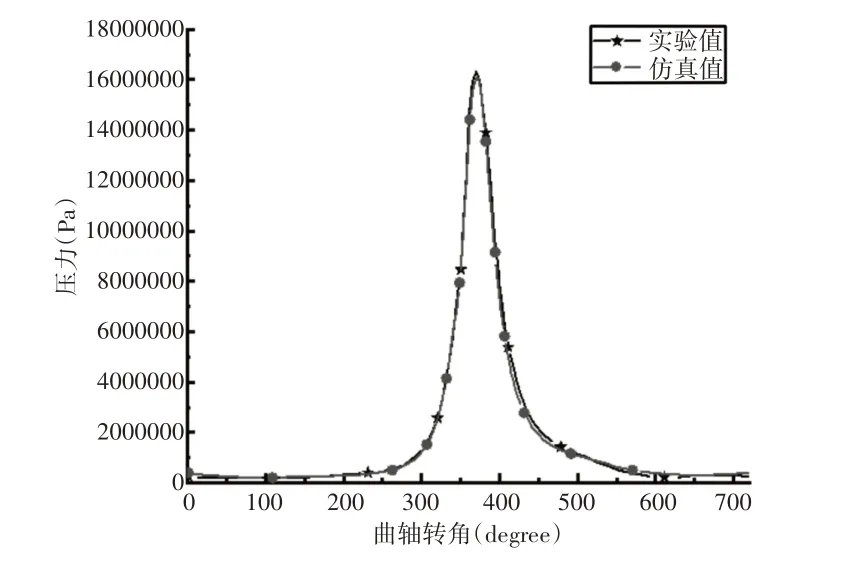
图4 缸内燃气瞬时压力曲线对比Fig.4 Comparison of Instantaneous Pressure Curve of In−Cylinder Gas
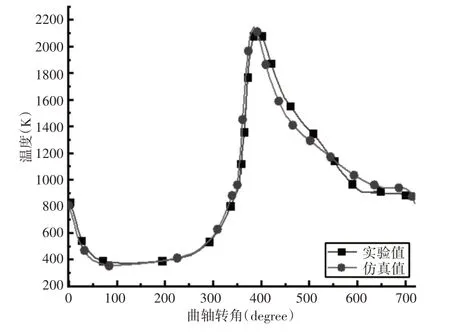
图5 缸内燃气瞬时温度曲线对比Fig.5 Comparison of Instantaneous TemperatureCurve of In−Cylinder Gas
缸内瞬时换热系数ℎg,采用Woschni[12]公式计算得到,公式为

式中:Tg—缸内燃气瞬时温度,℃;Pg—缸内燃气瞬时压力,MPa;D—活塞直径,m;Cm—活塞平均速度,m/s。
通过公式(6)计算得到缸内瞬时换热系数ℎg,如图6所示。已知缸内燃气瞬时换热系数ℎg和缸内燃气瞬时温度Tg,活塞上表面平均燃气温度Τgm和平均换热系数αgm由式(7)、式(8)计算得到。

图6 缸内燃气瞬时换热系数曲线Fig.6 Instantaneous Heat Transfer Coefficient Curve of In−Cylinder Gas

式中:θ—曲轴转角。
4.4 活塞内腔边界条件
该款柴油机采用喷溅冷却方式,活塞内腔具有良好的散热效果,内腔换热系数变化较小。内腔换热系数αoi计算公式为:

式中:θ—活塞顶厚度;λ—导热系数;Toi—曲轴箱气体温度;T1—内腔底部的温度;T0—活塞顶部温度。
通过以上公式计算并根据实验值确定额定工况下活塞的边界条件,如表2所示。对流热通量具体加载部位,如图7所示。

表2 活塞热边界条件Tab.2 Thermal Boundary Condition of Piston
4.5 边界约束
对模型进行约束时应尽量避免不合理的边界条件设置引起额外应力。如图7所示,设活塞对称面y=0及z=0设为绝热边界条件,且对称面设置模型具有对称性。活塞对称面y面设为x方向位移约束,x面设y方向位移约束,为避免活塞刚体z向平移,在活塞底面给定辊支撑约束。

图7 活塞边界Fig.7 Piston Boundary
5 计算结果分析
5.1 活塞温度场
T(400K),T(600K)、T(800K)分别为温度取400K、600K、800K下的物性参数计算得到的最高温度,如图8~图10所示。图11T(m)为考虑材料物性热效应的最高温度。如图8~图11所示,T(400K),T(600K)、T(800K)、T(m)的最高温度值分别为907K、897K、887K、892K。结果表明不考虑材料物性热效应与考虑材料物性热效应对最高温度影响较小,最高温度波动约2.25%,主要原因是最高温度位于陶瓷层,陶瓷材料的导热系数较小,且在高温环境下比较稳定。TBC阻隔热量传向基体,使活塞头部承受大量的热载荷,增加了活塞头部的温度梯度,最高温度均出现活塞顶面与燃烧室凹坑交界区域,如图8~图11所示。主要原因是此区域位于活塞表面的拐角处且承受两个方向的热载荷处,热阻较大,热量传递较少。

图8 T(400K)云图 Fig.8 T(400K)

图9 T(600K)云图Fig.9 T(600K)

图10 T(800K)云图 Fig.10 T(800K)

图11 T(m)云图Fig.11 T(m)
考虑材料物性热效应的活塞表层不同深度的选择按公差d为0.4mm 等差数列分布,提取轴θ=45°线不同深度温度变化曲线,如图12所示。陶瓷层上表面与下表面的平均温差为61.16K,TBC起到良好的隔热效果,但活塞头部温度梯度较大。通过图12看出活塞上表面的温度分布很不均匀,最大温度值波动约为131.3K。主要原因是活塞凹槽较深,槽底部离高温燃气较远。
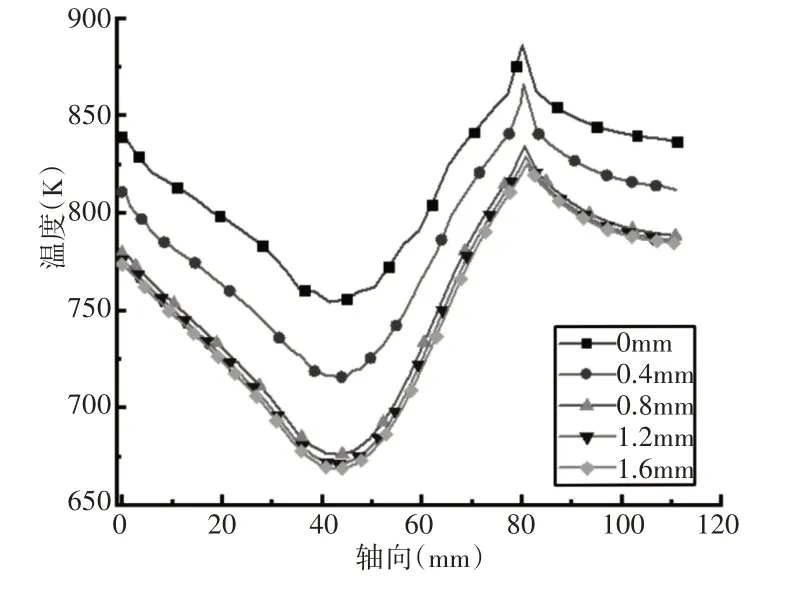
图12 活塞表层不同深度的温度变化曲线Fig.12 Temperature Profile of Different Depths of the Piston Surface
5.2 活塞热应力分析
σ(400K)、σ(600K)、σ(800K)分别为温度取400K、600K、800K下的物性参数计算得到的最大热应力,如图13~图15所示;图16σ(m)为考虑材料物性热效应的最大热应力。σ(400K)、σ(600K)、σ(800K)、σ(m)的最高温度值分别为438MPa、451MPa、498MPa、524MPa,如图13~图16所示。

图13 σ(400K)云图 Fig.13 σ(400K)
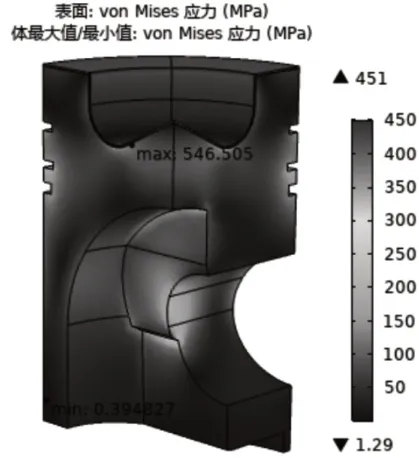
图14 σ(600K)云图Fig.14 σ(600K)
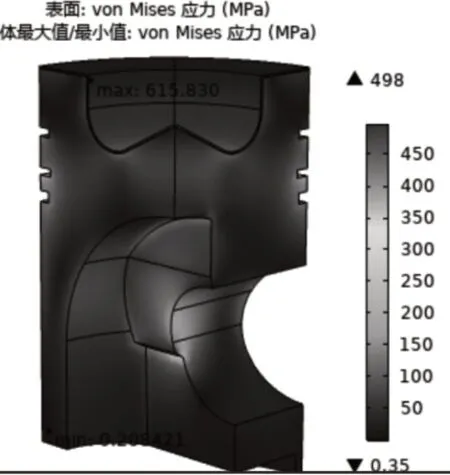
图15 σ(800K)云图 Fig.15 σ(800K)
结果表明不考虑材料物性热效应与考虑材料物性热效应的最大热应力有显著差别,最大值相差约86MPa。而且选用不同常物性计算得到的最大热应力、最小热应力及最大热应力所处位置不同,确定最大热应力易失效的区域难度较大,因此把材料物性热效应处理成常物性计算热应力问题的可靠性较低。
由于材料物性热效应对热应力的影响具有连续性,考虑材料物性热效应且温度升到最高值,材料物性热效应的变化趋于稳定,且物性热效应的波动对活塞热应力影响相对较小,其热应力计算有较高的可靠性,极限热应力为524MPa,其值比常物性的热应力大。
如图13~图16所示,体应力最大值均位于涂层交界区,体应力最小值均位于活塞裙部下端。

图16 σ(m)云图Fig.16 σ(m)
考虑材料物性热效应TBC活塞θ=45°平面上应力云图,如图17所示。如图17局部放大图所示,主要的热应力区域位于粘结层,最大热应力位于粘结层与基体的拐角处,主要原因是TBC阻隔大部分热量,而基体的热量相对较少,粘结层与基体间的温度梯度较大,热膨胀系数差别也较大,不利于热应力的释放。故粘结层与基体转折位置容易形成应力集中,容易导致TBC剥落失效。

图17 考虑热效应的活塞θ=45°平面上应力云图Fig.17 Piston with θ=45° Plane Stress Considering Thermal Effect
6 结论
(1)材料物性热效应对活塞最高温度的影响较小,最高温度波动约为2.25%,最高温度均位于活塞顶面与燃烧室凹坑交界区。陶瓷层上表面与下表面的平均温差约61.16K,隔热效果良好。
(2)随着温度升高,活塞材料的物性热效应变化越剧烈,考虑材料物性热效应的活塞热应力越大。当温度升到最高值,材料物性热效应的变化趋于稳定,热应力最大值为524MPa,其值比常物性参数的热应力值大。
(3)考虑材料物性热效应与常物性参数的TBC 活塞的最大热应力相差86MPa,而采用不同常物性计算得到的最大热应力及最大热应力所处位置不同,较难获得最大热应力易失效区域。因此把材料物性热效应处理成常物性计算热应力问题的可靠性较低。由于物性热效应对活塞热特性的影响具有连续性,因此考虑材料物性热效应更符合材料的热特性规律。
