立式发酵机搅拌阻力矩计算模型的搭建和修正
2022-04-28陈作炳罗传威
陈作炳,罗传威,郑 欢
(武汉理工大学机电工程学院,湖北 武汉 430070)
1 引言
随着科学技术的进步,畜禽养殖业向规模化、集约化和专业化的方向发展[1]。畜禽粪便中含有大量的病原微生物、重金属和氮磷等物质,不经处理直接排放会对土壤、水体和大气造成污染,甚至直接威胁人类身体健康[2−3]。为了高效处理大型养殖场的畜禽粪便,笔者设计出一种高效处理畜禽粪便的立式发酵设备。该设备利用微生物的好氧发酵来分解粪便中的有机物,实现畜禽粪便的无害化和资源化利用。
为了合理的设计该设备的传动系统,需要计算立式发酵机搅拌器满载工作时的阻力矩。国内大多数同类型设备计算阻力矩参照的是搅拌砂浆的计算公式[4],其阻力系数K需根据经验确定,具有不确定性。文献[5]建立了一套关联粉体搅拌功率的方法,但研究的物料颗粒没有粘性,并不满足其适用范围。国外多是研究搅拌器的搅拌效率和混合特性[6−7],对搅拌阻力矩计算模型的研究较少。
对发酵机内物料的运动情况做了合理的假设,建立了搅拌器阻力矩计算模型。基于相似理论缩减了搅拌器模型的尺寸,运用离散单元法模拟了搅拌过程,通过与现场应用试验数据的对比,验证了计算模型和相似模型离散元仿真的合理性,探究了搅拌转速对搅拌阻力矩的影响。
根据仿真结果对阻力矩的计算模型进行修正,为立式发酵机搅拌器阻力矩的计算提供了指导。
2 立式发酵机及其搅拌器
高效立式发酵机是一种新型多阶段移动发酵塔式发酵设备。立式发酵机整体结构图,主要由筒体、搅拌器、传动系统、上料系统、卸料系统和通风系统等几大部分组成,如图1所示。

图1 设备整体结构图Fig.1 The Structure of Machines
物料在立式发酵机内部堆积发酵,依靠自身重力从顶部向底部移动。发酵筒体内有3层不同的物料:上层刚进入的物料含水率约为55%。中间层正在发酵的物料含水率约为45%。底层经烘干的物料含水率约为30%。立式发酵机搅拌器的简化模型,搅拌器叶片的截面为三角形,如图2所示。确定搅拌器工作时的计算阻力矩,对于主传动的设计优化和整个设备性能的提升具有重要意义。
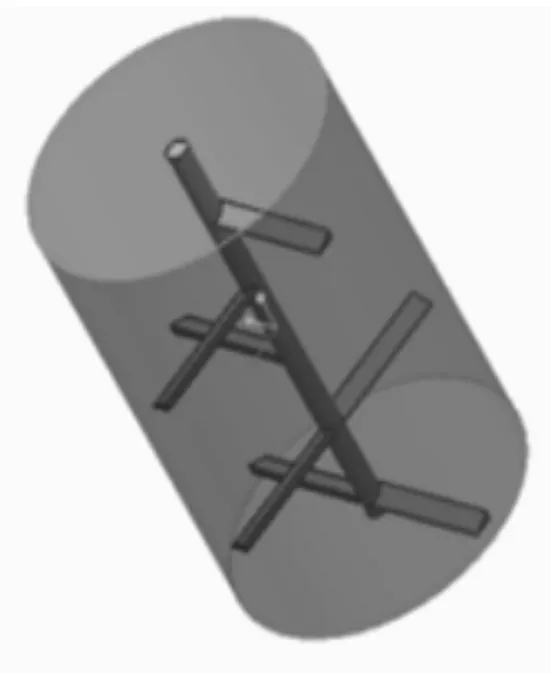
图2 简化几何模型Fig.2 Simplified Geometric Model
3 搅拌器运转阻力矩理论计算
由于搅拌器内的微生物对剪切运动很敏感,搅拌器的转速很低(3r/h),动载荷很小,阻力矩可采用静态的计算方法。
在这里假设满载工作时,物料孔隙率不变且没有轴向移动。物料对叶片的作用力,如图3所示。筒体内部物料对搅拌器产生的阻力矩可以分为两个部分,一是搅拌叶片推动物料时由物料对叶片的挤压力F产生的阻力矩,二是推动物料时由物料对叶片的摩擦力Ff产生的阻力矩。
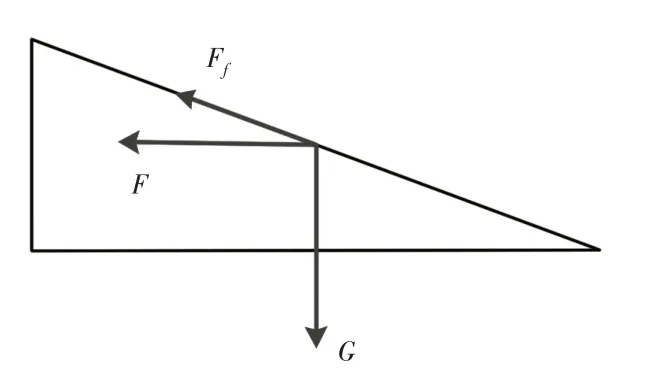
图3 物料对叶片的作用力图Fig.3 The Picture of Material Force on Blades
3.1 由物料对叶片的挤压力F产生的阻力矩
取单个叶片所在的圆柱区域为物料的运动区域,以圆柱的中心线建立柱坐标系,将运动区域内物料划分为足够小的n1个单元,如图4所示。取运动区域内任一单元体为研究对象,单元体距Z轴的距离为r,单元体夹角为dθ,弧长为rdθ,高度为dh1。

图4 单层运动区域的微单元划分Fig.4 Micro−unit Division of Single−Layer Motion Region
则物料对搅拌器的阻力矩:
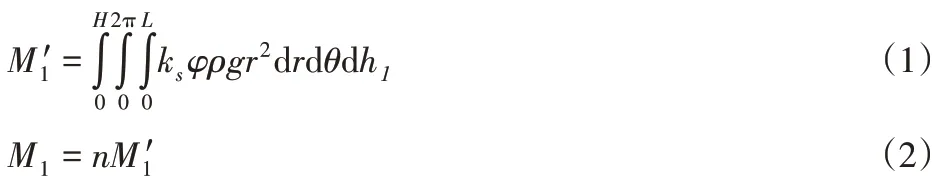
式中:M1′—单层运动区域内物料对搅拌器的阻力矩;M1—所有物料对搅拌器产生的挤压阻力矩;ks—叶片的形状阻力系数,叶片的截面为三角形,取1;φ—物料的填充率,取0.75;ρ—物料的密度,取750kg/m3;g—重力加速度,取9.8m/s2;H—单叶片所能搅动物料的高度,取0.16m;L—叶片长度,取1.7m;n—叶片的个数,取7。
3.2 由物料对叶片的摩擦力Ff产生的阻力矩
物料对叶片的摩擦力主要受叶片上部物料质量的影响,越靠近桶底的叶片所受的摩擦力越大。为了便于研究,将叶片上部的物料划分为n2个单元,单元距离主轴轴线为x,单元长为dx,宽为dy,高为dz。以第i个叶片为例,叶片所受摩擦力沿水平方向的分力:

式中:Mi′—物料对第i个叶片的摩擦力矩;M2—物料对所有叶片的摩擦力矩;ℎi—第i个叶片和物料顶部的距离;μi—物料和叶片间的摩擦系数,取值与叶片所在的物料层有关;α—叶片斜面和水平面的夹角,取25°;b—叶片宽度,取0.25m。搅拌器运转总阻力矩:

代入计算得:M=78634.98N ⋅m
4 搅拌器离散元仿真
4.1 相似理论和搅拌器的相似模型
对于这里所述的立式发酵机的有效容积为42m3,正常工作时颗粒数目达到4千多万,无法进行计算。运用相似理论对搅拌器模型尺寸进行缩小得到相似模型,减少计算颗粒数目,节省计算时间和计算机储存空间。采用质量、长度和时间3个基本物理量作为分析基础,对应的基本量纲分别用M、L和T表示。采用MLT 基本量纲系统[8],得到搅拌器相关参数量纲和指数表,如表1所示。

表1 相关参数量纲和指数表Tab.1 Related Parameter Dimensions and Indices
模型相似前后搅拌器材料相同,物料密度相同,重力加速度一致。将模型尺寸缩小25倍,通过π准则计算得到搅拌器相关参数相似关系,如表2所示。
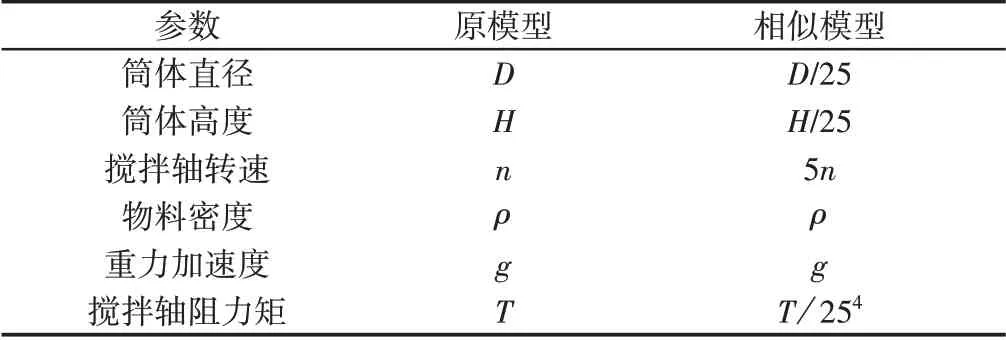
表2 相关参数的相似关系表Tab.2 Similarity Relationship of Related Parameters
4.2 物料接触模型的建立
立式发酵机中物料的建模,如图5所示,物料明显分为三层。发酵物料颗粒近似为球形,其中(1~2)mm的颗粒占4%,(3~4)mm的颗粒占10%,(5~6)mm 的颗粒占60%,(7~8)mm 的颗粒占20%,(9~10)mm的颗粒占6%。

图5 物料离散元计算模型Fig.5 Discrete Element Calculation Model of Materials
发酵物料带有粘弹性,与含水率有关,每层物料间的粘接力有差异。物料颗粒间的接触模型选择Hertz−Mindlin with JKR(Johnson−Kendall−Roberts)Cohesion凝聚力接触模型,可以模拟强沾性的干、湿颗粒[9]。在这个模型中法向弹性接触力取决于颗粒重叠量、相互作用参数和表面能量:

式中:FJKR—法向弹性接触力;α—相互接触颗粒的接触圆半径;γ—表面能;δ—颗粒重叠量;E∗—当量杨氏模量;R∗—当量半径。
4.3 搅拌器离散元仿真
根据相似关系在Creo 中建立搅拌器的相似模型,导入到EDEM中进行模拟仿真。在立式发酵机运转的过程中,用Hertz−Mindlin with JKR模型模拟拟畜禽粪便废料与搅拌转子之间的相互作用,仿真计算搅拌转子的阻力矩。查阅相关文献资料[10−11],物料的泊松比为0.25,剪切模量为1×108Pa,密度为750kg/m3;钢材的泊松比为0.3,剪切模量为1×1010Pa,密度为7850kg/m3。物料和物料的恢复系数为0.35,静摩擦系数为0.3,动摩擦系数为0.1;物料和钢材的恢复系数为0.32,静摩擦系数为0.2,动摩擦系数为0.11。
物料从筒顶进入到筒体中堆积发酵,设置(0~6)s为底层物料的装填阶段,其表面能为0.015 J m2;(6~13)s为中间层物料的装填阶段,其表面能为0.018 J m2;设置(13~16)s为上层物料的装填阶段,其表面能为0.02 J m2。(17~40)s为搅拌器稳定工作阶段。搅拌阻力矩随时间变化的曲线,在(0~16)s,搅拌阻力矩随着物料的增多而增加,如图6所示。随着所加物料粘性力的增加,三个加料阶段阻力矩的变化率也增加。(17~40)s,搅拌阻力矩的数值逐渐稳定在一个定值,为0.2026N ⋅m。根据相似关系,原模型的搅拌阻力矩为79034.98N ⋅m。搅拌器一直在运转,筒体内始终有少部分物料在起伏,搅拌轴的阻力矩仍然会有微小的波动。
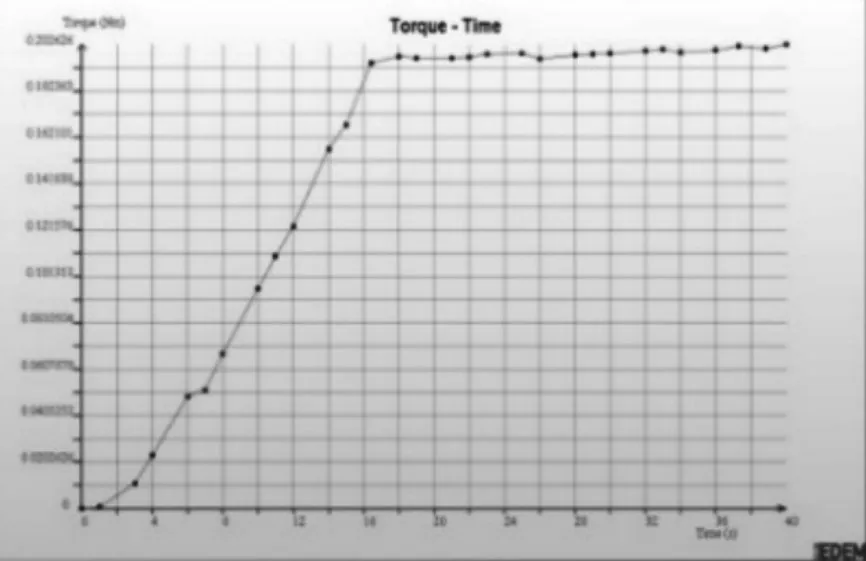
图6 搅拌器转矩曲线Fig.6 The Curve of Stirring Resistance Moment
4.4 立式发酵机现场应用试验
在沈阳进行立式发酵机现场应用,投入的物料为蘑菇渣和猪粪的混合物,经过7天的好氧发酵,输出的产品经过烘干打散后成为有机肥,实现猪粪便的无害化和资源化利用。物料的添加量为设备总高的80%,使通风系统高效工作。
通过控制柜中的变频器观察主电机的输出功率和输出转速。变频器的输出数据,如图7所示。主电机的输出功率为0.3kW,输出转速为298.3r/min。可以计算出主电机的输出扭矩:

图7 现场应用数据图片Fig.7 Data Images of Field Application

则搅拌器的阻力矩:T=i×T1×η=80197.9 N ⋅m
式中:P—电机输出功率;n—电机输出转速;i—传动系统减速比,取8800;η2—传动系统效率,取0.94。
理论计算、相似离散元仿真、和现场测试得到的搅拌器阻力矩,如表3所示。仿离散元模拟和现场实验得到的搅拌阻力矩误差不超过5%,验证了相似模型离散元计算的合理性。理论计算和仿真模拟得到的搅拌阻力矩误差不超过1%,说明搅拌器转速为3r/h时,搅拌阻力矩的计算是可以忽略动载荷的。

表3 搅拌器的阻力矩Tab.3 Resistance Torque of Agitator
5 搅拌器阻力矩计算模型的修正
上述理论计算模型是在忽略动载荷的条件下推导的,为了更好的应用于工程实际,还需探究动载荷对搅拌器搅拌阻力矩的影响,并据此对计算模型进行修正。在这里我们仅探究转速为0.05r/min、0.1r/min、0.15r/min、0.2r/min、0.25r/min、0.3r/min 和0.35r/min的搅拌阻力矩。取各转速下物料稳定后的搅拌阻力矩,并用MAT‐LAB软件对其进行拟合,如图8所示。这里研究的是低转速情况下的搅拌阻力矩的计算模型,其粘性力不会改变,摩擦系数不会变化,由摩擦力产生的阻力矩不发生改变。转速的变化会影响物料对搅拌叶片的挤压力。这里我们采用多项式拟合公式为:

图8 转矩拟合曲线Fig.8 Fitting Curve of Torque

式中:kv—动载系数;ki—i次幂的系数;n—搅拌器转速,r/min。二次拟合的相关系数R2=0.9746,三次拟合的相关系数R2=0.9912,四次拟合的相关系数R2=0.9968。为了使计算公式简便且更贴合实际,这里取三次拟合公式。

立式发酵机搅拌器的阻力矩为:

当n≤0.05r/min,kv=1;当0.05 r/min (1)立式发酵机低速运转时,对搅拌器内物料的运动作了合理的假设,建立了适用于低速运转的立式搅拌器运转阻力矩的计算模型。 (2)对搅拌器模型进行缩放,通过π准则建立了相似模型和原模型的相似关系,运用Hertz−Mindlin with JKR 模型建立物料颗粒间的接触模型,根据筒体内物料的性质建立了离散元计算模型。通过与现场应用试验数据的对比,验证了计算模型和相似模型离散元仿真的合理性。 (3)用离散元仿真模拟6种转速下的稳定搅拌阻力矩,并根据仿真结果对理论计算模型进行修正。用多项式拟合搅拌转速与搅拌阻力矩的关系,得到了用于低速运转的立式搅拌器运转阻力矩的计算模型。6 结论
