基于信息融合及模糊FMECA的小子样系统可靠性增长设计研究

王保昌，周金宇，庄百亮

（1.江苏理工学院“结构/材料多尺度协同设计与制造”江苏省高校优秀科技创新团队，江苏 常州 213001；2.机械科学研究总院江苏分院有限公司，江苏 常州 213001）

1 前言

系统的可靠性增长研究工作是一个重复“试验—改进—再试验”的过程，通过试验暴露出系统的故障，分析故障原因并采取相应的改进措施，随后再进行试验，重复上述步骤，可以确保可靠性稳步增长，最终达到规定数值[1]。

系统故障分析常用的方法主要有故障树分析（FTA）和故障模式影响及危害性分析（FMECA），通过分析系统故障，给出相应的改进措施来提高系统的可靠性。

但是系统故障模式的分散性较强，失效或故障可检测的程度不一样，有的症状难以直接观察，故障发生的可能性难以得到准确描述等特点使得故障模式的质量评估带有很强的模糊性。在对故障模式做危害度评价的过程中，由于个体间认识的差异，给定量分析添加了很多主观色彩，而且随着影响因素的增多，各因素互相制约、互相影响，很难客观地给出综合评判结果[2]。此外，在小子样系统中，由于数据匮乏，难以对系统进行准确的可靠性评估[3]，给系统的可靠性增长工作带来了极大的困难。

针对上述问题，这里将基于相关函数的多源信息融合方法及模糊FMECA故障分析方法综合运用于小子样系统的可靠性增长设计研究中，解决小子样系统数据匮乏及模糊信息的影响，对系统进行准确的故障分析和评估，制定有效的改进措施提升系统的可靠性。

最后以某新型冲压机的可靠性增长设计为例对这里提出的方法进行了验证。

2 可靠性增长建模

2.1 Bayes模型

由于贝叶斯可靠性增长模型可以有效利用产品的试验数据和工程信息预测可靠性，符合小子样、复杂系统的特点，它从20世纪80年代以来有了长足的发展，是可靠性增长模型研究的重点。

考虑某个随机试验，在这个试验中，有n个不相容的基本事件B（ii=1，2，…n），记A为试验中可能发生的任一事件，在离散情况下的贝叶斯定理为：

式中：P（A│B）i—条件概率；P（Bi│A）—后验信息；P（B）i—先验信息。在连续条件下，贝叶斯定理表示为：

式中：θ—分布参数；X—观测数据样本；

Θ—参数取值空间；

π（θ）—先验分布密度函数；

π（θ│X）—验后分布概率密度；

（fX│θ）—参数θ给定之后，X的密度函数。

2.2 基于相关函数的多源信息融合方法

复杂系统的统计推断问题[4]与验前信息有很大关系，利用多源信息融合方法[5−6]融合多种验前信息，可以保证统计推断具有较高的置信度。这里采用基于相关函数的多源信息融合方法来构建融合验前分布。设系统的可靠性指标随机变量为T，概率密度为（ft│θ）。通过现场试验获得n个故障间隔时间数据X={t1，t2，…，tn}，此外有相似型号故障数据、仿真数据、专家经验等z个信息源t1（i），...，tn（i）（i=1，2，…，z），则：

式中：π（iθ）—每个信息源的验前分布，i=1，2，…，z；

π（θ）—所有信息源的融合验前分布；εi—权系数。

式（3）中需要根据相关函数计算权系数εi，令：

式中：u′—第i个信息源验后分布的期望；

uj—每个信息源验前分布的均值，j=1，2，...，z；

u—融合验后分布的期望；

b′ki、bk—未知常数，k=0，1，...，z。

通过每个信息源的验前和验后分布采用抽样技术分别产生z+1组随机样本，用每组样本的均值分别替代式（4）中的u′i及uj，从而对b′ki进行求解。

通过融合验后分布采用抽样技术产生z+1组随机样本，用每组样本的均值分别替代式（5）中的u，同时利用每个信息源验前分布的随机样本均值分别替代式（5）中的uj，从而解出含有权系数εi的bk表达式。

将求解出的b′ki及含有权系数εi的bk表达式带入式（6）中，求出含有权系数εi的相关函数表达式，随后将其带入式（7）中，通过对z组方程组进行求解，求出权系数εi的值。

式中：ηπiπ—相关函数；

—每组信息源验后分布的方差。

从信息论的角度，（一）方面，该方法在确定融合权重的过程中，充分考虑各单一验后分布与融合验后分布的相关程度，可以充分体现各来源验前信息的质量；（二）方面，该方法充分利用了多源验前信息，在融合验后分布基础上进行统计推断，增强了统计推断结论的稳健性。

3 基于信息融合的可靠性指标估计

3.1 模型假设

实践证明，机械产品的寿命分布以Weibull分布[7−8]、对数正态分布等为主要分布形式，这里假设系统寿命T服从双参数Weibull分布，其分布函数为：

概率密度函数为：

式中：t—测试时间；m、η—形状参数和尺度参数。

通过现场试验获得n个失效数据X={t1，t2，…，tn}，其中tk为失效时间，k=1，2，...，n。此时条件分布为：

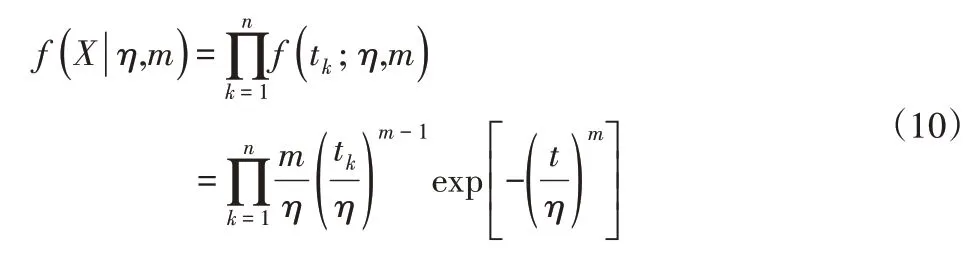
3.2 可靠性指标估计

假设有两组信息源，且样本数据均为独立同分布，每组参数m、η的先验分布分别为π（1m）、π（1η）及π（2m）、π（2η），每组信息源的联合验前分布为：

根据式（3）可以得到两组信息源的融合验前分布，其数学拟合式为：

根据式（2）求得参数m、η的联合验后分布为：

参数m、η的验后边际密度分别为：

式中：k1、k2—常数，其值可以通过下式求解；

在Bayes模型中，参数的估计可选用后验分布的某个位置特征量，如后验分布的众数、中位数、期望值或最大后验值[9]。

为了减少估计误差，这里采用后验均值作为参数的估计值，两参数的估计值分别为：

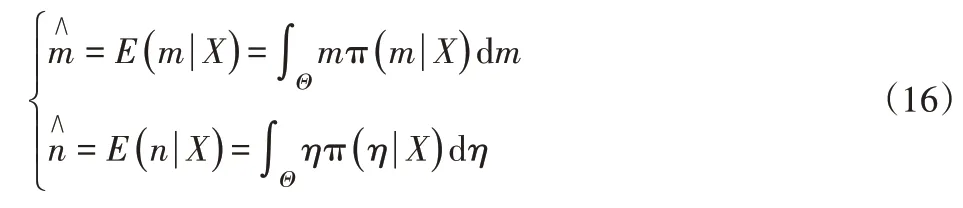
于是，可靠度和失效率的点估计分别为：

4 模糊FMECA故障分析及改进措施

在利用FMECA 对系统进行故障分析时经常会遇到大量模糊信息，在这种情况下难以对故障模式进行准确的综合评价。

针对此类情况可以将模糊理论与FMECA相结合，构成模糊FMECA[10]，通过模糊FMECA 分析解决模糊信息的影响，以改善FMECA方法的不足。

模糊FMECA分析的步骤为：

（1）建立因素集

因素集是影响评估对象的各因素集合，通常用字母U来表示，即

式中：Ux—第x个影响因素，x=1，2，…，n。

（2）建立评价集

式中：Vl—评价集的第l个等级，l=1，2，…，m。

（3）建立模糊因素评价矩阵

模糊综合评价一般由H人组成评价小组，小组中的成员分别对影响因素Uxk评出一个因素水平Vl。当H位成员中评定Uxk隶属于Vl的有Hxlk个人，就得到U的评价集为：

式中：rxlk—第x个影响因素的评价集，l=1，2，…，m；

k—第k个故障模式。

将得到的n个模糊评价向量依次排列组成矩阵，即为模糊因素评价矩阵

（4）确定各个影响因素权重集

设第k个故障模式的因素加权项为w，其权重集为：

（5）I级模糊综合评价

当权重集Wk和评价矩阵Rk已知时，就可以得到第k个故障模式的I级模糊综合评价，即：

式中：Bk—故障模式k的I级模糊综合评价向量。

（6）确定模糊危害度等级

为了能够得到更加清晰的评价结果，需要对Bk进行加权平均法处理，得到一个具体的数值Ck来表示故障模式k对系统的综合危害等级，即：

式中：VT—评价集V的转置向量。

（7）Ⅱ级模糊综合评价

Ⅱ级模糊综合评价中因素集的组成是I级模糊评价的各故障模式，保持评价集V不变，由评价小组重新确定各因素的权重向量W，按照I级模糊评判的思想进行，就可以得到Ⅱ级模糊综合评价。

在通过模糊FMECA方法对系统进行综合评价后，需要将各潜在故障模式按照危害度从大到小的顺序进行排序，按照此顺序先后采取相应的改进措施，提高系统的可靠性。

5 应用实例

某新型冲压机的主要系统组成，如图1所示。

图1 冲压机主要系统组成Fig.1 Main System Composition of Stamping Machine

该机经现场试验得到的故障间隔时间数据X1={92，310，445，283，606，408，224，383，534，379}，试验数据服从两参数Weibull分布。

此外有来自该机仿真数据及类似型号冲压机的故障数据，分别为Y1={185，402，124，553，398，672，530，375，490，208}，H1={230，102，423，502，610，439，420，275，198，401}。

下面按这里所述的方法对该冲压机进行可靠性增长设计研究。

5.1 原机可靠性指标估计

采用抽样技术分别对Y1、H1两组数据进行500 组的随机抽样，根据式（16）计算每组再生样本的尺度参数和形状参数值并进行分布拟合，通过观察两个参数的经验曲线、概率密度函数曲线的形状特点确立两组参数均服从Weibull分布。

通过参数估计，确定各参数的先验分布分别为：

式中：πY1(m)、πY1(η)—仿真数据Y1的形状参数和尺度参数的验前分布；πH1(m)、πH1(η)—类似型号冲压机故障数据H1的形状参数和尺度参数的验前分布。

根据式（11）可以分别得到两组参数的联合验前分布，其数学拟合式为：

利用这里所述的权系数求解方法，求得权系数ε1和ε2的值分别为0.917、0.083。于是融合验前分布为：

试验样本失效数据个数为10，根据式（10）求得条件分布为：

根据式（13）可以得到融合验后分布π（m，η│X1），随后利用这里所述的参数求解方法求得参数m、η的估计值分别为1.54、431.27，于是原冲压机的可靠度R（t）及失效率λ（t）的点估计为：

5.2 模糊FMECA分析及可靠性增长措施

在进行模糊FMECA 分析前，这里根据设计、制造和使用者的经验以及类似冲压机的维修信息，确立了机床每个零部件可能发生的故障模式，之后基于模糊FMECA对各种潜在故障模式进行了模糊综合评价，以故障模式C−0207 为例，其模糊评价过程为：

（1）确定该型冲压机的影响因素U为：U={故障概率，严重度，检测难易程度，维修难易程度}；

（2）这里设立5个评价等级，即V={1，2，3，4，5}；

（3）经过评价小组的评价，确认该故障模式的故障概率集R1={1.2，0，0，0，0}，严重度集R2={1，1，0，0，0，0}，难易程度集R3={0，0.4，0.4，0，0.3}，维修难易程度集R4={0.6，0.4，0，0，0}，评价矩阵R为：

（4）由评价小组确立的因素权重集W为：

（5）根据式（24）求得该故障模式的Ⅰ级模糊综合评价B为：

（6）根据式（25）求得该故障模式的模糊危害度C为：

式中：VT—评价集V的转置向量。

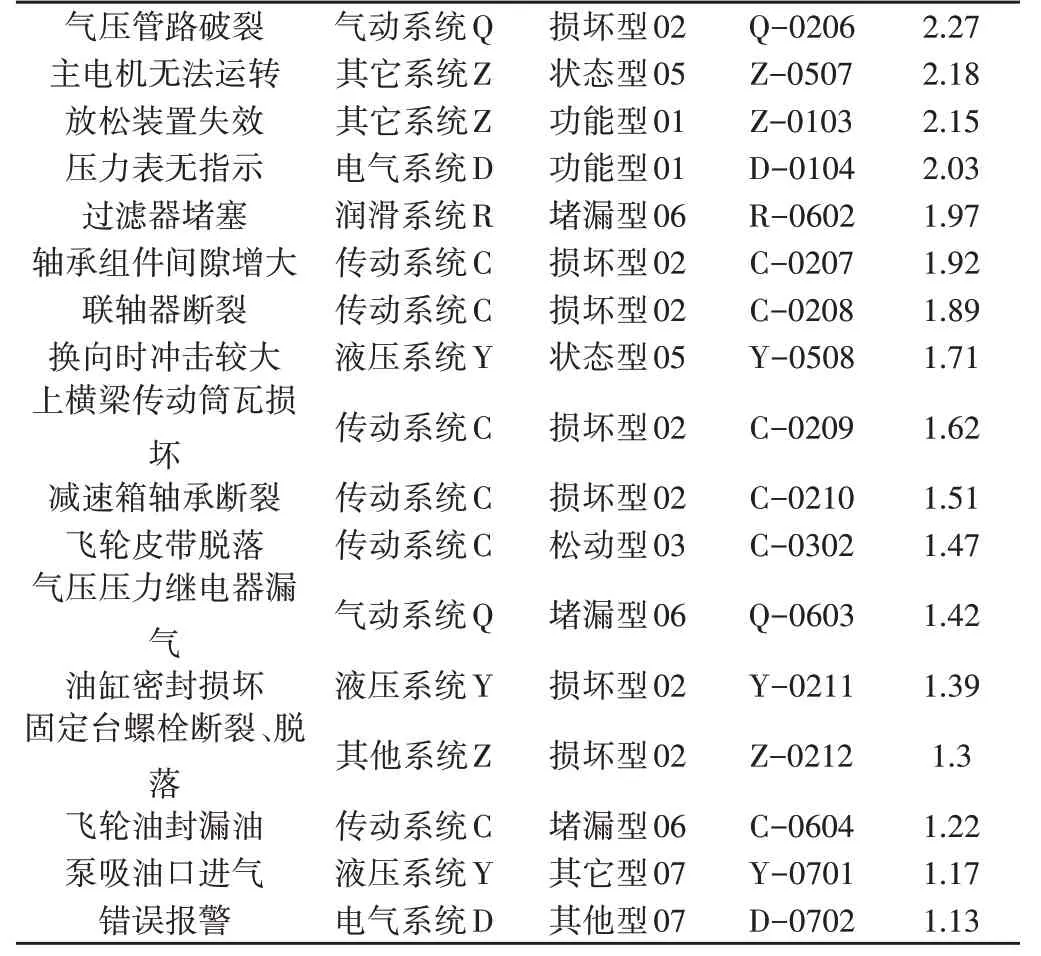
通过相同的方法获得全部潜在故障模式的模糊危害度，如表1所示。

表1 冲压机故障模式模糊危害度等级排序表Tab.1 Fuzzy Hazard Ranking Table of Stamping Machine Failure Mode

气压管路破裂主电机无法运转放松装置失效压力表无指示过滤器堵塞轴承组件间隙增大联轴器断裂换向时冲击较大上横梁传动筒瓦损坏减速箱轴承断裂飞轮皮带脱落气压压力继电器漏气油缸密封损坏固定台螺栓断裂、脱落飞轮油封漏油泵吸油口进气错误报警气动系统Q其它系统Z其它系统Z电气系统D润滑系统R传动系统C传动系统C液压系统Y传动系统C传动系统C传动系统C气动系统Q液压系统Y其他系统Z传动系统C液压系统Y电气系统D损坏型02状态型05功能型01功能型01堵漏型06损坏型02损坏型02状态型05损坏型02损坏型02松动型03堵漏型06损坏型02损坏型02堵漏型06其它型07其他型07 Q−0206 Z−0507 Z−0103 D−0104 R−0602 C−0207 C−0208 Y−0508 C−0209 C−0210 C−0302 Q−0603 Y−0211 Z−0212 C−0604 Y−0701 D−0702 2.27 2.18 2.15 2.03 1.97 1.92 1.89 1.71 1.62 1.51 1.47 1.42 1.39 1.3 1.22 1.17 1.13

从表中可以看出元器件的损坏以及液、气、油渗漏等问题占了很大的比例，因此，在选择设备零件的采购来源时应特别注意零件的质量，确保系统具有较高的初始可靠性。为进一步提升系统的可靠性，这里根据表中的潜在故障模式分别给出了相应的故障原因及改进措施，具体内容，如表2所示。

表2 冲压机故障模式原因及可改进措施表（续）Tab.2 Stamping Machine Failure Mode Reasons and Improvement Tables（Continued）

Y−0701管路松动D−0702检测系统发生故障紧固管路并定期开放气阀排气联系厂商设计人员检测维修

表2 冲压机故障模式原因及改进措施表Tab.2 Stamping Machine Failure Mode Reasons and Improvement Tables

D−0102 Y−0402 R−0504 Q−0205 Y−0601溢流阀平衡缸震动导出油管变形或Q−0505 C−0403 C−0506 Q−0206 1.旋转凸轮发生故障；2.计数器损坏1.阀的工作压力设定太低；2.阀体或密封件磨损产生内部泄漏设定值不当致紧固螺栓松开，现裂缝有杂质进入油管泄压阀阀芯卡死或弹簧失效变频器过流、过载、过压等故障1.制动力调整过小；2.制动带损坏气压压力过大、温度过高Z−0507 1.电机线路脱落或断线；2.冲床热继电器跳动或损坏Z−0103 1.放松电磁阀无动作；2.放松凸轮角度过小导致放松动作未完成D−0104 R−0602 1.管内污物淤积阻塞；2.扇形齿轮与小齿轮阻力过大密封损坏，油液中进入杂质C−0207组件间存在间隙，在冲击作用下间隙越来越大C−0208 Y−0508 C−0209振动导致传递扭矩不均1.换向时瞬时关闭、开启造成动能或势能相互转换时产生冲击；2.阀芯卡死润滑不良1.更换微动开关；2.检修更换1.重新调整设定压力；2.检查修复或更换新备件重新设定溢流阀参数紧固螺栓重新紧固并采取措施减小震动情况更换油管并定期清洁保证油液清洁并更换、维修泄压阀定期保养及备件更换1.适当调大制动力；2.更换制动带调整气压压力和温度，更换管路1.检查并上紧螺丝，连接线路；2.按下热继电器复位手柄，或更换热继电器1.更换电磁阀；2.调节放松凸轮角度，延迟放松时间，使冲床气动送料机放松夹板放松时张开足够的距离1.用钢丝疏通污染物2.调整配合间隙至适中更换密封件并保证清洁工作采用通过检验的、口碑好的品牌的轴承，此外，采取滑动轴承和滚动轴承混合使用的设计防止轴承问隙过大影响滑块下死点精度设置减震装置并保证润滑1.延长换向时间；2.设计并更换带缓冲的阀芯更换筒瓦并保证润滑

5.3 改进后新机的可靠性指标估计

对改进后的冲压机进行可靠性增长试验，得到的故障数据X2={394，630，589，830，230，1020}，此外实施改进措施后得到新机的仿真数据及类似型号冲压机故障数据分别为Y2={436，642，1123，346，598，632}，H2={639，348，423，1089，610，647}。

按照原机的可靠性指标计算方法求得改进后新机的形状参数和尺度参数分别为1.07、598.15，于是改进后新机可靠度R（2t）及失效率λ（2t）的点估计为：

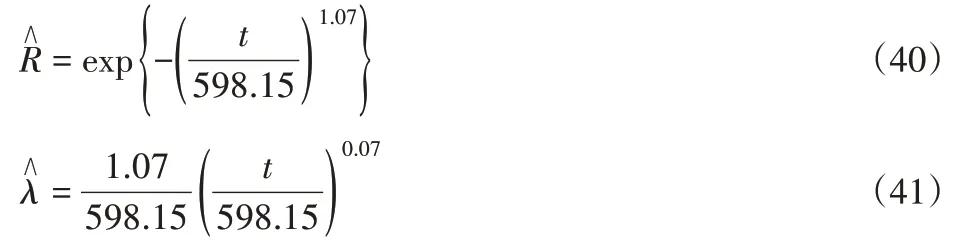
根据式（33）、式（39）和式（34）、式（40）绘制了该冲压机改进前后可靠度及失效率的曲线变化对比图，如图2、图3所示。

从图2中可以看出在时间间隔[0，300h]内改进前后冲压机的可靠度基本一致，当超过300h后，原机的可靠度开始急剧下降，最终在1300h时可靠度达到最低点，而改进后新机的可靠度下降较缓，直到2800h后达到可靠度最低点，可靠性远远超过了原机。

图2 冲压机改进前后可靠度曲线对比图Fig.2 Reliability Curve Contrast Diagram of Press Before and After Improvement

从图3中可以明确地看出在时间间隔[0，3000h]内，改进后新机的失效率基本浮动在（0.0015~0.0022）之间，比原机的失效率低了数倍，系统可靠性得到了极大的提升。

图3 冲压机改进前后失效率曲线对比图Fig.3 Failure Rate Curve Contrast Diagram of Press Before and After Improvement

6 结论

针对小子样系统数据少且存在模糊信息不易进行准确的可靠性增长分析和评估的情况，这里将基于相关函数的多源信息融合方法及模糊FMECA故障分析方法综合运用于小子样系统的可靠性增长设计研究中，并以某新型冲压机为例，通过模糊FMECA方法对冲压机的潜在故障模式进行了分析，给出了各潜在故障模式的故障原因及改进措施，结合信息融合方法先后将实施改进措施前后的仿真数据、类似型号冲压机故障数据与现场试验数据融合，根据Bayes方法对原机和新机的可靠性指标进行了评估，并绘制出它们的可靠度及失效率函数对比图，通过函数对比图来看，实施改进措施后的新机可靠性明显高于原机，极大程度的实现了系统的可靠性增长。

因此，这里所提出的方法是可行、有效的，对小子样系统数据少且信息模糊情况下的可靠性增长分析和评估具有一定的借鉴意义。