汽车EHB系统控制策略研究

李 娜，陈 勇，2

（1.北京信息科技大学机电工程学院，北京100192；2.北京电动车辆协同创新中心，北京100192）

1 引言

汽车是人们最重要的交通工具，随着汽车相关技术的发展，智能化已经是人们关注的焦点，也是汽车的发展方向之一。为了满足智能化汽车的功能需求，制动系统作为执行机构中的一个重要组成部分，应具有常规制动、时效制动、ABS、TCS、ACC等功能。汽车线控制动系统是用电控系统代替了传统的以液压为主的制动系统，大大提高了汽车制动时的安全性与稳定性[1]，线控制动系统目前分为电子液压制动系统EHB（Electro−Hydraulic Brake）和电子机械制动系统EMB（Electro−Mechanical Brake）。EHB系统有制动备份，因此比EMB系统更可靠[2]。国外对EHB系统的研究已相当成熟，博士公司的iBooster、大陆公司的MKC1等，国内文献[3]在线控液压制动系统的稳定性、响应特性等方面进行了大量研究。

汽车安全行驶是人们最关心的问题，EHB系统作为一种快速响应系统，执行机构的动态响应特性对制动控制效果起着至关重要的作用，响应速度越快、越稳定汽车行驶越安全。因此建立起EHB的液压系统模型、研究液压系统动态特性、评价液压元件性能、设定液压元件性能目标及制动系统主动控制算法都具有重要的意义。为了进一步研究EHB 系统的动态响应控制，根据EHB系统结构建立相应的数学模型，此外，基于前人的理论研究，提出了遗传算法优化PID控制和模糊自适应PID控制策略，利用AMESim 和Matlab/Simulink 软件联合仿真进行验证。这对研究车辆EHB系统动态响应特性具有一定的借鉴意义。

2 EHB系统数学模型

EHB系统是在传统液压制动系统的基础上增加了部分电器元件，主要由轮速、轮缸压力等传感器、电控单元和执行器机构等部分构成。控制单元和执行机构布置比较集中，使用制动液作为制动力的传递媒介，因此被称为集中式、湿式制动系统。传感器将所采集的制动信息传递给电控单元ECU，ECU计算处理制动信息，分析驾驶员制动意图并根据控制策略确定控制信号并发送至制动操作单元，制动液压力升高推动制动轮缸活塞进行制动[4]。

对EHB系统主要元件进行数学建模。

2.1 高速开关电磁阀

高速开关电磁阀控制着制动液在轮缸里的流入和流出，由基尔霍夫电压定律得：

由牛顿第二定律得：

式中：R—电磁阀电阻；U—电压；i—电流；δ—阀芯与定铁芯的气隙宽度；s0—阀芯与定铁芯的气隙横截面积；μ—真空磁导率；l—磁导体的有效长度；y—阀芯运动位移；N—电磁阀的线圈匝数；Ф—电磁阀磁通量；ms—阀芯总质量；Ks—电磁阀弹簧的弹性刚度；B—速度阻力系数；y0—电磁阀弹簧预紧力[5]。

2.2 制动管路

根据流体连续性方程知：

式中：V—管路的总体积；Ap—管路的横截面积；Ke—管路的体积弹性模量；d—管路的直径；L—管路的长度；ρ—制动液密度；Rf—层流的管路摩擦力。

2.3 制动轮缸

盘式制动器在轿车上应用广泛，其结构简单制动效果较好。在轮缸建立压力过程中，制动液推动轮缸活塞进行制动，以制动钳和活塞为研究对象，由流体连续性方程和牛顿第二定律得：

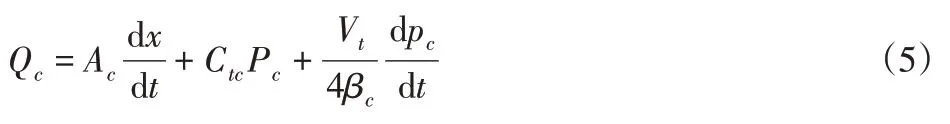
式中：Qc—制动液流量；x—活塞位移；x0—弹簧预紧量；Vt—制动轮缸的容积；Ctc—液压缸的总泄漏系数；Ac—轮缸活塞的有效截面积；Pc—制动压力；β—制动液的体积弹性模量；Fc—活塞所受制动液推力；mc—制动钳与活塞的总质量；Bc—活塞运动阻尼系数；Kc—弹簧的弹性刚度[5]。

2.4 EHB液压系统模型

建立单车轮液压制动系统模型，在增压过程中，忽略温度变化、制动轮缸的弹性变形等次要因素，由以上式子及相关式子通过拉氏变换可得以下EHB系统数学模型为：

式中：Ka—气体刚度系数；Ca—阻尼系数；A—蓄能器的横截面积。

3 模糊自适应PID控制实现

3.1 模糊自适应PID控制

PID控制有着鲁棒性好、可靠性高、适应性强的特点，同时具有精度低、抗干扰能力差等缺点[7]。模糊逻辑算法是智能控制中应用最广泛的算法之一，模糊自适应PID 控制以PID 算法为基础，用模糊规则进行模糊推理，以误差和误差变化率作为输入，是一种PID参数自整定的过程[8]。为了更精确的控制EHB系统，采用模糊自适应PID控制策略对轮缸压力进行控制，从而提高EHB系统的动态响应特性。

图2 模糊自适应PID控制系统结构图Fig.2 Structure Diagram of Fuzzy PID Control System

模糊控制器采用两个输入和三个输出，将误差e和误差变化率ec作为输入，其中误差e代表期望轮缸压力值与制动轮缸反馈实际压力的差值，将PID的三个参数比例系数Kp、积分系数Ki、微分系数Kd作为输出。误差e和ec的模糊论域分别为［−6 6］和［−1 1］，两者所对应的模糊子集为{NB，NS，ZE，PS，PB}，Kp的模糊论域为[0 1]，Ki和Kd的模糊论域为[−1 1]，三者所对应的模糊子集为{ZE，ZO，PS，PM，PB}。输入输出隶属度函数都采用三角函数[8]。

表1 Kp的模糊控制规则表Tab.1 Fuzzy Control Rule of Kp

表2 Ki的模糊控制规则表Tab.2 Fuzzy Control Rule of Ki

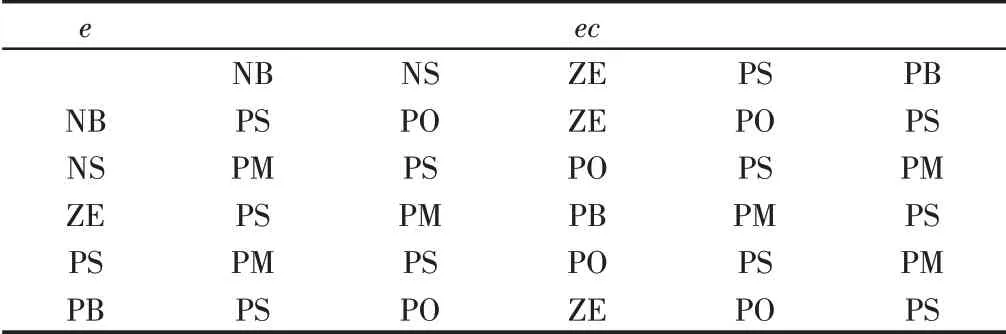
表3 Kd的模糊控制规则表Tab.3 Fuzzy Control Rule of Kd

在Matlab软件的Simulink模块中，设置AMESim联合仿真接口，根据上述模糊控制规则、隶属度函数及系统原理等，搭建模糊自适应PID控制系统，以期望轮缸压力值与制动轮缸实际压力的差值及差值变化率作为模糊PID系统的输入，联合仿真，从而实现模糊自适应PID对EHB系统轮缸压力的控制，如图3所示。

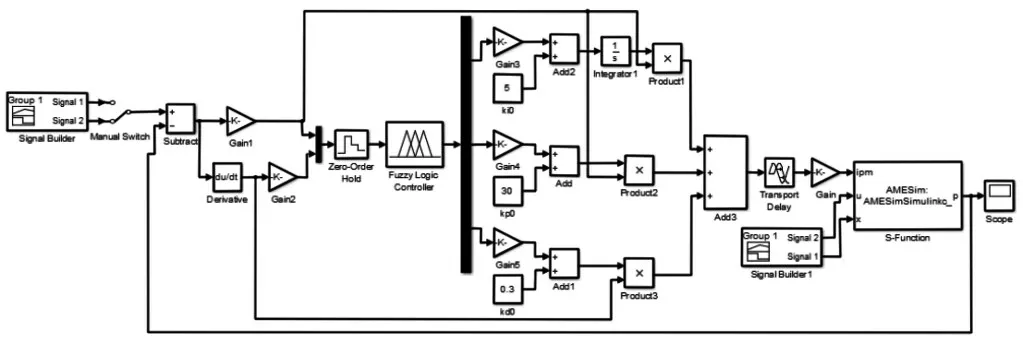
图3 模糊自适应PID仿真模块Fig.3 Simulation Module of Fuzzy PID Control

3.2 EHB系统的仿真模型

以单车轮制动系统为研究对象，根据汽车EHB系统结构及其原理在AMESim 中搭建单车轮制动系统模型。采用AMESim仿真系统，只需直接拖动模型方框到要仿真的系统中，设置参数即可。制动轮缸建模需综合考虑材料和机械特性，比较繁琐困难，将其简化，在AMESim 中利用阻尼元件与弹性元件，缸和活塞，以及一个可以做平动的质量块来搭建轮缸模型。在建模过程中，忽略了如液压介质的泄漏、制动轮缸的弹性变形、各个零部件的磨损、温度的可变性等影响系统的一些次要因素[6]，EHB系统模型的搭建，如图4所示。

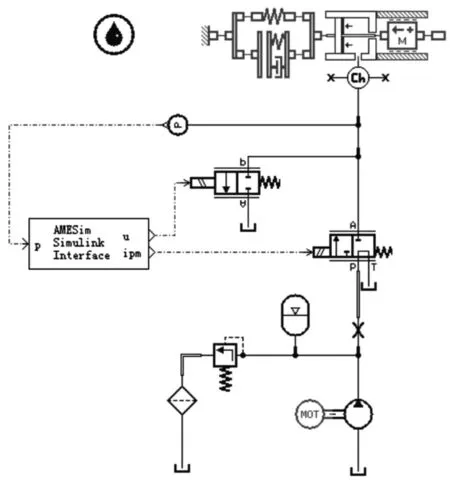
图4 EHB系统模型联合仿真模块Fig.4 Joint Simulation Module of EHB System

在AMESim软件仿真界面中根据仿真模型实际需要设置参数产生Simulink 联合仿真接口，在Simulink 环境中利用s−func‐tion功能产生与AMESim联合仿真接口，并将其它模块添加到仿真系统中，从而实现AMESim和Simulink的联合仿真。

遗传算法产生于20世纪六七十年代，它的主要思想来自生物遗传学的“优胜劣汰、适者生存”，是一种通过模拟自然进化过程来搜索最优解的方法[9]。

图5 遗传算法主要算法过程流程Fig.5 Main Algorithm Process Flow of Genetic Algorithm

AMESim软件中有专门的遗传算法优化模块，这为设计和研究带来了方便。利用AMESim中的遗传算法模块优化EHB系统模型中PID的三个参数，使得EHB系统轮缸压力能够最快达到期望轮缸压力且稳定性较好。

在AMESim中搭建好EHB系统模型后，由于PID三个参数值偏大或偏小都可能影响到轮缸压力曲线对目标压力的跟随性，根据AMESim的软件特点，在模型中用批处理方式观察PID三个参数对轮缸压力的影响进而确定三个参数的大概范围，在批处理过程中，三个参数的输入值如下：

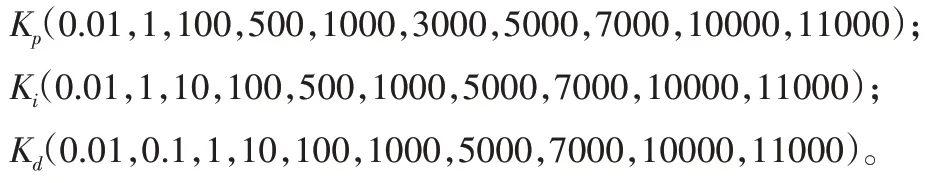
通过批处理的仿真分析，以轮缸压力跟随目标值效果为判定依据，舍去偏离目标轮缸压力较大的压力曲线所对应的PID三个参数的值，最终确定三个参数的大概范围为K（p1~3000），K（i1~1000），K（d0.1~1000）。在此范围内寻找最优PID三个参数值，任取三个参数的初始值为Kp=30，Ki=5，Kd=0.3。

为了改善系统的动态及稳定特性，需要对系统加入一些约束和要求，系统的参数设置，如图6所示。

图6 参数控制模块Fig.6 Module of Parameter Control

在AMESim软件中遗传算法优化模块中，以轮缸压力变化为约束条件，根据遗传算法参数值的一般选择范围，设置种群数量为30，种群再生率为0.8，为了使结果更精确，遗传算法的终止进化代数值取100，变异概率为0.03，突变幅值为0.2，如图7所示。经过AMESim系统计算仿真，遗传算法优化PID三个参数的最终值为：Kp=1591.45，Ki=1.0117，Kd=7.937。

图7 遗传算法参数设置界面Fig.7 Parameter Setting Interface of Genetic Algorithm

在遗传算法优化PID 参数控制策略中，EHB 系统单车轮模型，如图8所示。根据以上遗传算法优化结果设置PID的三个参数，即可实现该控制策略对EHB系统轮缸压力的控制。

图8 EHB系统仿真模块Fig.8 Simulation Module of EHB System

5 仿真分析

制动安全性是制动系统首先要考虑的，制动系统响应时间越短意味着制动距离越短[10]。以期望轮缸压力信号作为输入信号，在模糊自适应PID控制和遗传算法优化PID控制策略下分别输入不同信号，通过观察图像中轮缸实际压力到达期望轮缸压力值的快慢，来比较两种控制策略对提高EHB系统动态响应特性的有效性。

普通轿车行驶过程中制动轮缸压力一般为6MPa 至8MPa，最大不超过12.5MPa，在此压力范围内，任取4MPa、6MPa、8MPa和12MPa分别代表轻度制动、中低度制动、中高度制动和重度制动四种制动工况下汽车期望轮缸压力值，并在四种制动工况下对汽车轮缸压力进行仿真分析。

5.1 阶跃信号下的仿真分析

采用阶跃信号模拟车辆紧急制动工况，在第0s进行信号输入，以期望轮缸压力信号为输入信号，任取目标轮缸压力值6MPa和12MPa，仿真时间为1s，在遗传算法优化PID控制、模糊自适应PID控制和无控制策略情况下分别得出EHB制动系统增压过程中轮缸压力变化曲线，如图9、图10所示。

图1 EHB系统控制原理图Fig.1 Control Schematic of EHB System

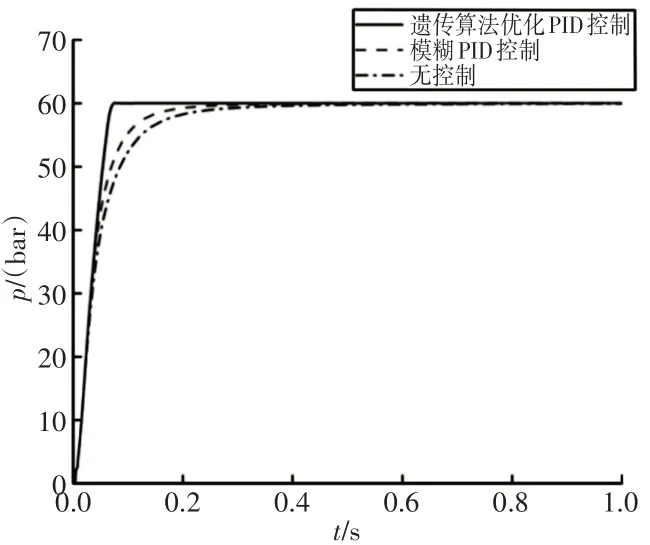
图9 目标轮缸压力为6MPa的仿真曲线Fig.9 Simulation Curves with Target Pressure of 6MPa

图10 目标轮缸压力为12MPa的仿真曲线Fig.10 Simulation Curves with Target Pressure of 12MPa

由图9和图10可知，轮缸压力超调量较小，控制效果较好，但不同控制策略下，系统响应速度差别较大。当不同大小的阶跃轮缸压力信号输入后，轮缸迅速增压，超调量接近于零。在遗传算法优化PID控制中，轮缸达到目标压力的时间约为0.1s，所用时间最短；在模糊PID控制和无控制下，轮缸达到期望压力的时间分别为0.2s和0.3s左右。

5.2 方波信号下的仿真分析

采用方波信号模拟理想状态下车辆行驶过程中突然制动又突然停止制动的工况，任取压力值为4MPa、频率为1Hz和压力值为8MPa、频率为0.66Hz的方波信号作为输入信号，仿真时间分别为2s和3s，得出EHB系统增压、保压和减压过程中轮缸压力变化曲线，如图11、图12所示。

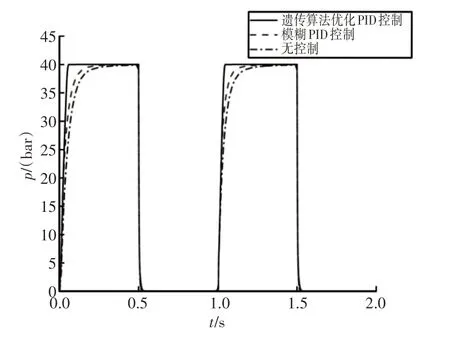
图11 压力4MPa、频率1Hz的仿真曲线Fig.11 Simulation Curves of Pressure 4MPa and Frequency 1Hz

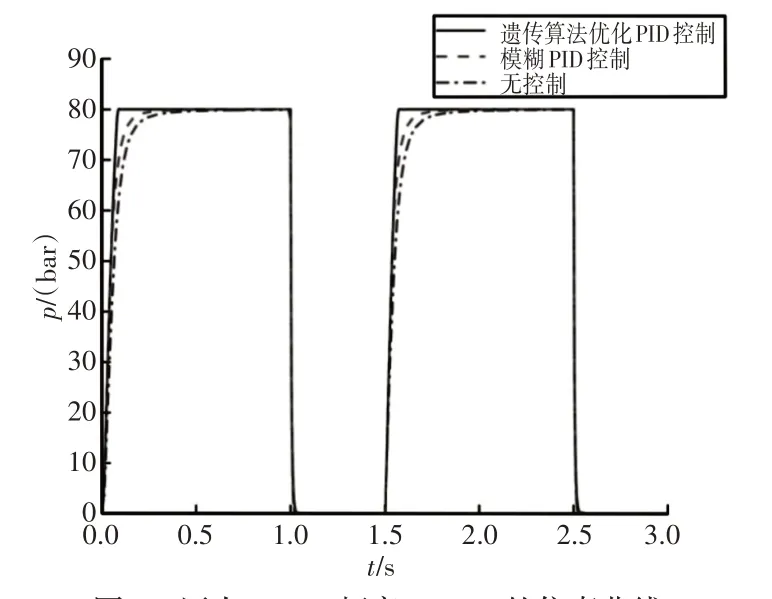
图12 压力8MPa、频率0.66Hz的仿真曲线Fig.12 Simulation Curves of Pressure 8MPa and Frequency 0.66Hz

由图11、图12可知，当输入不同压力、不同频率的方波信号时，两种控制策略下的轮缸压力曲线都能很好地跟随目标轮缸压力，轮缸增压过程比减压过程所用时间长。

在遗传算法优化PID控制中，轮缸压力达到目标压力最快，所用时间约为0.1s；在模糊PID控制策略下，轮缸达到期望压力的速度略慢一些，为0.2s左右；无控制策略下轮缸到达目标压力所用时间最长，为0.3s左右。

6 结论

建立了EHB 系统数学模型及AMESim 液压模型，分别研究了遗传算法优化PID 控制和模糊自适应PID 控制策略对汽车EHB系统响应特性的影响。结果表明：

（1）当输入阶跃信号和方波信号时，在遗传算法优化PID控制和模糊自适应PID控制下的轮缸压力对目标轮缸压力跟随性较好，轮缸压力超调量接近零，控制效果良好。

（2）在不同控制策略下EHB系统响应时间方面，与模糊PID控制相比，遗传算法优化PID控制所用时间减少约0.1s；与无控制策略相比，模糊PID控制所用时间减少0.1s左右。因此遗传算法优化PID控制和模糊自适应PID控制策略能够提高EHB系统的动态响应特性，并且前者所用时间最短，控制效果最好，这对以后研究提高EHB系统响应特性提供了理论依据。