基于DIP的沥青混合料车辙变形数值模拟
2022-04-28吕悦晶蒋云云周兴林
吕悦晶,蒋云云,周兴林,汤 文
(武汉科技大学汽车与交通工程学院,湖北 武汉 432000)
1 引言
车辙是影响沥青路面使用性能的主要问题,也是道路维修费用的主要来源之一。因此,大量的实验和研究集中于建立不同加载条件下沥青面层永久变形预测方法和模型上[1−2]。众所周知,用于道路建设的沥青混合料是由集料,沥青砂和孔隙组成的多相材料。沥青混合料的力学性能很大程度上取决于代表混合物骨架的集料级配。车辆在路面上移动而产生的应力主要通过粗集料相互接触所形成的接触点传递。因此,沥青混合料的内部结构对道路和基础设施工程具有重要的应用价值,对沥青混合料的内部结构进行研究是很有必要的。近年来,基于数字图像处理(DIP)或计算机X射线断层扫描技术,已经尝试用于获取沥青混合料的内部结构和力学建模的目的。如文献[3]采用DIP对20个不同岩石类型和尺寸的集料样品进行分析,并将分析结果与传统人工方法所得结果进行比较,DIP与人工测量结果具有很强的相关性,表明DIP法是颗粒形状测量的较好替代方法。文献[4]使用工业CT对砾石进行了研究,利用DIP对切片图像进行反色,中值滤波,降噪,二值化等集料特征的捕获,借助MIMICS实现了对集料的三维重构。文献[5]将DIP和有限元技术相结合,定性地分析了沥青混合料模型在间接拉伸模式下的受力状态。文献[6]利用CT扫描设备获得了沥青混合料的三维内部细观结构,即集料,砂浆和孔隙的空间分布,建立了沥青混合料的离散元模型,对沥青混合料的动态模量进行预测。
大多数研究集中在集料的细观结构重构,沥青混合料的动态模量预测上,到目前为止,从沥青混合料的细观角度研究沥青混合料车辙变形发展规律的相关研究较少。因此,这里拟使用DIP和有限元技术,在ANSYS中建立沥青混合料非均质有限元模型,分析沥青混合料的永久变形规律。
2 数字模型的建立
2.1 使用的数字图像方法
数字图像分割是将图像细分为与某种像素相一致的不同区域的过程,这种分割与图像分割的目的有关。此操作是区分图像中感兴趣的子区域的第一步,在本研究中,指沥青混合料中集料部分。图像分割应该满足以下条件:
(1)对于所选择的特征,检测到的区域应尽可能均匀;
(2)区域边界应与所采用的相似特征的变化兼容;
(3)被视为统一的区域不应进一步划分为次区域;
(4)小而复杂的区域不应与相邻的区域合并。
为了从车辙试件切片图像中识别沥青砂和集料,使用以下图像方法。(1)一种基于Otsu法的阈值分割算法;(2)Canny边缘检测算子实现了区域边界的检测。在集料边缘检测后,为了提高所用算法的性能,必要时还可以通过滤波器对图像进行处理。
2.1.1 数字图像的阈值分割
图像分割是把图像分成若干个有意义的区域的处理技术,是将各像素进行分类的过程。在沥青混合料车辙试件截面图像中,通常较轻质量的细集料与较深背景颜色的沥青砂分散在一起。为了对图像进行阈值分割,基于他们灰度上的差异将图像区分为目标和背景是可行的。通过假定合适的阈值,该图像被划分为具有不同灰度值的不同区域。每个区域仅包括其强度低于或高于阈值的一个像素。通过修改阈值,检测到的区域形状或数目也会发生变化。设置不同的阈值,图像有不同的分割方式。
为了确定阈值,需要对灰度直方图的形状进行分析。本研究借助文献[7]中车辙实验材料及结果数据,其集料级配,如表1 所示。沥青混合料车辙试件切片图像,如图1 所示。其灰度直方图,如图2所示。由于灰度直方图显示出强烈的双峰特性,集料和背景的灰度差较大,可以将谷底点所对应的灰度值作为阈值,然后根据该阈值进行分割,就可以将集料从图像中分割出来。

图1 车辙试件截面图像Fig.1 Cross−Sectional Image of Rutting Specimen

图2 灰度图像直方图Fig.2 Gray Image Histogram

表1 集料级配Tab.1 Complete Aggregate Gradatio
2.1.2 边缘拾取
边缘本质上是图像局部特性的不连续性、灰度或结构等信息的突变处。文献[8]提出的边缘检测算法是一种有效且性能良好的边缘检测算法,是在有噪声轮廓的情况下推导出的边缘检测最优化算子。该算法是分阶段实现的。如下所示:
(1)使用高斯滤波器对图像进行平滑,它主要用于降低噪声;
(2)计算梯度的幅值和方向;
(3)通过非极大值抑制法实现阈值化梯度幅度。它用于区分边界上的点;
(4)利用高低阈值处理、跟踪边缘得到集料轮廓;
在使用canny边缘检测算子处理截面图像时,可能会出现轮廓线不闭合的情况,可通过对图像进行多次膨胀再腐蚀的操作,如图3所示。分别为操作前后的集料边缘检测图。

图3 边缘检测图Fig.3 Edge Detection Diagram
相关研究表明[9],粒径小于2.36mm 细集料对沥青混合料的抗车辙能力贡献不大,为了提高计算机的计算效率,减少后续模型计算时长,将小于2.36mm的集料与沥青胶浆合并,得到的集料与沥青胶浆边缘轮廓,如图4所示。

图4 车辙试件边缘轮廓图Fig.4 Edge Profile of Rutting Specimens
2.2 几何模型
通过DIP,将处理后的沥青混合料边缘轮廓图导入到AN‐SYS,生成了沥青砂和粗集料的二相非均质有限元几何模型,如图3所示。从图中可看出集料形状与沥青混合料车辙试件中的粗集料的形状吻合良好,说明了DIP的适用性。
2.3 材料参数
沥青砂材料特性的表征对研究沥青混合料的车辙变形具有重要的意义。此外,温度和环境条件也会影响材料对荷载的响应。沥青砂在一定频率和温度范围内具有粘弹塑性,表征沥青砂的这种材料有多种方法,如复数模量[10],蠕变[11]等。文献[7]中以Burgers模型来表征沥青砂的材料性质,如表2所示。由于ANSYS中表征粘弹性材料的性质只有Prony级数。故需要将Burgers模型参数转化为Prony级数所对应的参数,转化过程如下所示:

表2 沥青砂的Burgers模型参数Tab.2 Burgers Model Parameters of Asphalt Sand

式中:E1,η1—Maxwell刚度系数和粘度系数;E2,η2—Kelvin 刚度系数和粘度系数;ε—应变;σ—应力。
ANSYS中内置的Prony剪切模量表达式为:

式中:αi—相对剪切模量松弛时间。
Burgers模型的本构方程:

以剪切模量表示式(3)时,

进行Laplace和Laplace的逆变换后可得剪切模量Prony级数表达式:
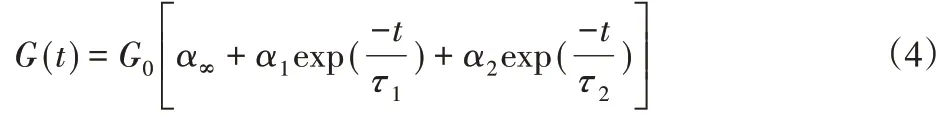
则可得到:

α1,α2,τ1,τ2—ANSYS 中粘弹性材料的输入值,本研究中视集料为线弹性材料,其弹性模量—55.5GPa[7]。
3 模型验证
由于二维虚拟车辙实验的加载方式不同于实验室车辙实验,参考相关文献的研究成果[12],采用静态荷载等效方法,在二维虚拟车辙实验中,车轮在试样表面上某一点上的累计加载时间被视为总加载时间,如式(5)所示。在60℃和0.7MPa,施加和车辙试件[13]相同的边界条件,如图6所示。即对非均质有限元模型的左右两侧施加X方向的约束,对底部施加X,Y方向的约束,对车辙试件加载60min,模型对沥青混合料车辙深度的预测。非均质有限元模型随时间变化的预测曲线,如图7所示。

图6 车辙深度预测云图Fig.6 Rutting Depth Prediction Cloud Map

图7 预测车辙深度−时间关系曲线图Fig.7 Predicted Rutting Depth−Time Curve

式中:T—车辙实验加载时间;t—累计加载时间。
从图6 中可以看到,在荷载作用区域,车辙深度最大值为−7.07276mm,随着荷载作用区域的距离增大,其车辙深度在不断减小,最小值为0.223647mm,说明远离荷载作用区域一定距离后,该沥青混合料截面发生一定程度的隆起变形,这是因为当轮载作用于沥青混合料试件时,其内部产生了剪应力,发生了剪切变形。在荷载作用下方,集料的质心位置发生了明显的移动,集料质心之间的间距减小。从图5可以看出,该非均质有限元模型的车辙深度预测值大于实测值,这是因为沥青混合料中粗集料形成的粗骨架承担着主要的抵抗外部变形的作用,然而数字试件中的集料比实验室试件的集料少,集料之间的接触嵌挤作用相对来说更小,预测值与实验值最大相差16%,说明用此非均质有限元模型研究沥青混合料的车辙变形规律是可行的。

图5 有限元模型图Fig.5 Finite Element Model Diagram
4 影响沥青混合料车辙深度的其他因素
4.1 沥青胶浆模量的影响
由于文献[7]中建立的沥青混合料离散元模型中只有粘弹性Burgers 模型参数,因此这里同时变化Burgers 模型参数的(0.2~1.0)倍的方式来表示沥青砂模量的变化,称为沥青砂的模量系数。通过改变沥青砂模量系数,得到模量系数—车辙深度关系曲线。从图中可以看到,对于同一条曲线而言,随着模量系数的增大,沥青混合料的车辙深度在不断的减小,在60℃条件下沥青胶浆模量系数0.2到0.4阶段最为明显。从40℃和50℃模量系数—车辙深度关系曲线中可以明显的观察到两者车辙深度有一个突变,且随着沥青胶浆模量系数的减小,其车辙深度差值在不断的扩大。而过了50℃后,其车辙深度差值相对较小,说明当温度超过沥青软化点时,沥青胶浆模量系数的减小,会加剧减小沥青混合料抗车辙性。
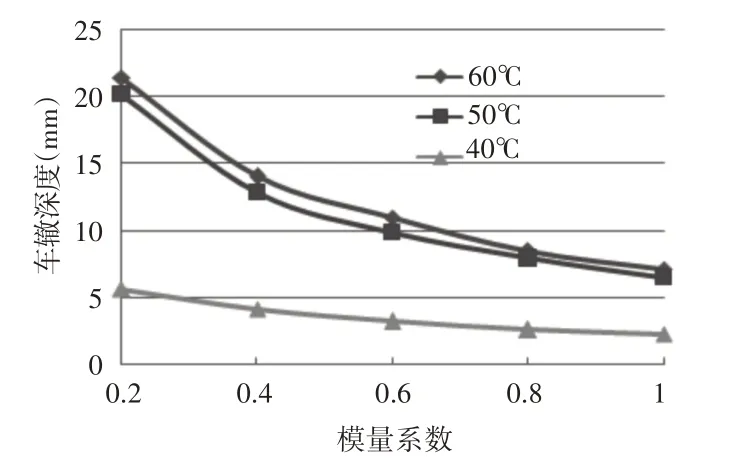
图8 模量系数−车辙深度关系曲线Fig.8 Modulus Coefficient−Rutting Depth Curve
4.2 粗集料模量的影响
下图列出了粗集料模量−车辙深度关系曲线。粗集料取值是依据文献[14]中集料范围所选取的,如图9所示。依次为35GPa,40GPa,45GPa,50GPa,55.5GPa。从图中可以看到,在同种温度条件下,提高集料的模量值,对沥青混合料的抗车辙能力影响不大。

图9 粗集料模量−车辙深度关系曲线Fig.9 Modulus−Rutting Depth Curve of Rough Aggregate
从40℃和50℃这两条粗集料模量−车辙深度关系曲线中可以看出,当温度达到了沥青砂的软化点,虽然其车辙深度也在不断的增加,其最大值为在60℃条件下35GPa到55.5GPa,集料模量增长了58.5%,其车辙深度也相应的下降了41.3%。这表明集料模量的增加不能有效的抵抗沥青混合料的整体变形,沥青砂作为沥青混合料中最柔软的一部分,可见提高沥青胶浆的模量可以更好的提升沥青混合料的整体的剪切模量,从而抵抗因轮载而产生的的沥青混合料永久变形。从实践的角度来说,提高集料的模量可能不能有效的提高沥青混合料的抗车辙能力。
4.3 骨料移动的影响
了解粗集料的移动情况有助于理解车辙产生的内在机理。待虚拟车辙实验完成后对不同加载时刻粗集料颗粒的质心位置进行统计,得到集料最大竖向位移变化,如图10所示。集料在加载过程中,竖向移动速率呈现出先增大后减小的变化,与车辙深度曲线呈现出相同的变化趋势。在40℃时,由于温度低于沥青砂软化点47℃,在加载初期,集料移动距离较小但移动速率较快,随着温度的升高,沥青砂变得柔软,沥青混合料的高温稳定性急剧下降,但由于集料接触点的增多,逐渐形成稳定的骨架结构,增强了其抗车辙能力,导致集料向下的移动速率下降。因此,选用密级配的集料级配在软化点以上时可以较好的提高沥青混合料的抗车辙能力,低于软化点时影响不大。
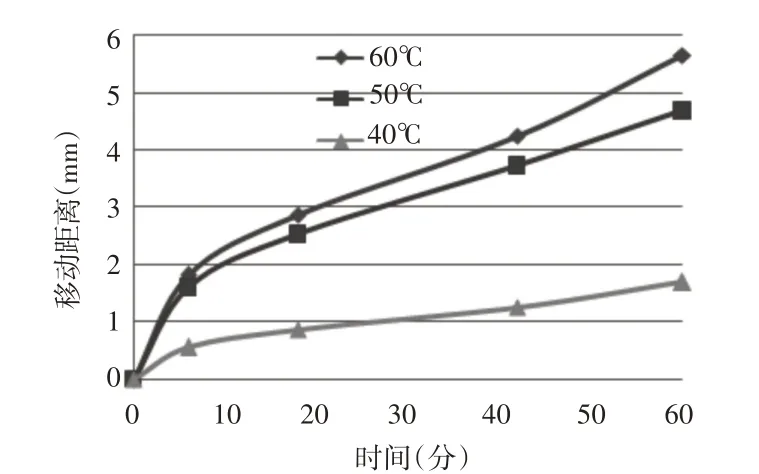
图10 时间−质心竖向移动距离曲线Fig.10 Time−Center of Mass Vertical Moving Distance Curve
5 结论
(1)本研究利用DIP,提取了集料的边缘轮廓,为后续分析车辙变形规律提供了基础。
(2)本研究所提出的非均质有限元模型可以预测沥青混合料的车辙深度。通过文献中的实验数据和非均质二维有限元模型的数值模拟结果,发现两者具有较高的相似性,证明了此非均质有限元模型的适用性。
(3)从非均质角度分析了沥青混合料车辙变形规律,为沥青混合料的设计提供了理论指导。通过分析得出,提高集料模量对其影响不大,低标号的沥青砂对沥青混合料的抗车辙能力的提升呈现出先增大后减小的趋势,密级配的集料级配就提升抗车辙能力而言与温度相关,在软化点以上时可以较好的提高沥青混合料的抗车辙能力,低于软化点时影响不大。
