自适应MCKD和ALIF的滚动轴承早期故障诊断
2022-04-28袁邦盛易灿灿
袁邦盛,肖 涵,易灿灿
(1.冶金装备及其控制教育部重点实验室,武汉科技大学,湖北 武汉 430081;2.湖北省机械传动与制造重点实验室,武汉科技大学,湖北 武汉 430081)
1 前言
滚动轴承是机械传动系统中的重要零部件,广泛应用于机械设备中。
滚动轴承的运行状况直接影响设备的生产效率和安全。在机械设备的实际运行中,如果不能及时识别滚动轴承的早期故障,故障的冲击会加速滚动轴承的损坏并最终导致重大事故,严重影响正常生产。因此,监测和诊断滚动轴承的运行状态对轴承早期故障研究具有重要的意义[1−3]。
Sawalhi在2007首次将最小熵反褶积(MED)[4]用于轴B承与齿轮的故障诊断中。文献[5]通过MED和VMD的方法成功提取风电机组发电机滚动轴承故障,但对较弱的早期轴承故障具有一定的局限性。因此针对MED的局限性,国内外许多学者做了大量的研究,文献[6]提出相关峭度反褶积(MCKD)算法,用以提高信号相关峭度值和信噪比,同时增强淹没在信号中的连续脉冲。目前,MCKD算法在大型滚动轴承故障诊断研究中得到了较多的应用,文献[7]将MCKD与谱峭度相结合对风电机组和热轧带钢轧机的振动信号进行诊断,提取滚动轴承的故障特征。文献[8]采用MCKD和经验模态分解(EMD),从强背景噪声中提取风力发电机组轴承早期故障特征。虽然EMD算法[9]可以将复杂信号分解为多个固有模态函数(IMFs),但该方法没有明确的理论基础,存在模式混叠、分解误差较大等问题,因此,基于EMD的轴承故障特征提取准确性不足。2016年文献[10]提出的自适应局部迭代滤波(ALIF)对非线性、非平稳信号具有较好的分解效果,将Fokker−Planck微分方程的基础解系作为滤波函数,设计了一种局部、自适应、稳定的迭代滤波方法。目前,ALIF算法在故障诊断领域得到了进一步的研究与应用,文献[11−12]将ALIF 与能量算子解调相结合应用于滚动轴承故障特征提取,唐贵基等人提出ALIF−HT方法应用于汽轮发电机组转子故障诊断。与EMD相比,ALIF可有效的抑制模式混叠现象。
由于MCKD滤波器参数(长度L、位移数M)的选取往往由人为经验确定,存在较大的偶然性和随机性,最终影响降噪效果。为了更准确地提取轴承故障特征,提出了一种自适应MCKD与ALIF相结合的故障诊断方法,通过分析故障轴承模拟信号和实测信号,表明该方法对轴承的早期故障特征具有较强的识别效果。
2 算法介绍
2.1 最大相关峭度反褶积
故障轴承高速运转,会产生周期性连续脉冲时间序列x(n),模拟噪声时间序列e(n)与系统响应为ℎ(n),构成滚动轴承故障的时间序列y(n):

MCKD的实质是通过寻找一个RIF滤波器ω(l),将采集到的故障信号y(n)恢复到原始输入信号x(n)即:

当相关峭度达到最大值时,MCKD迭代结束。原始信号进行MCKD运算后,冲击成分得到增强。相关峭度定义为:
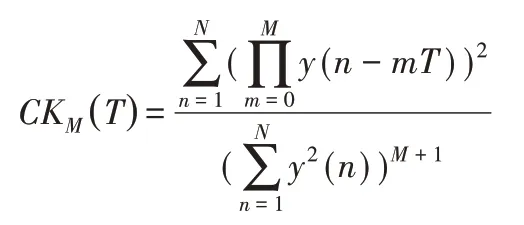
式中:M—位移数;T—冲击信号周期。
优化MCKD算法的目标函数:

其中,l=1,2,3…,L。
寻找最优滤波器ω(l),使MCKDM(T)最大,即:
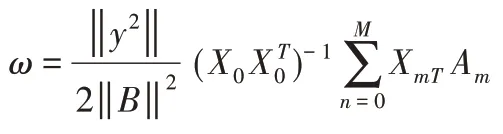
用矩阵形式来表示求解得到的滤波器结果如下:

其中,

MCKD算法具体流程,如图1所示。
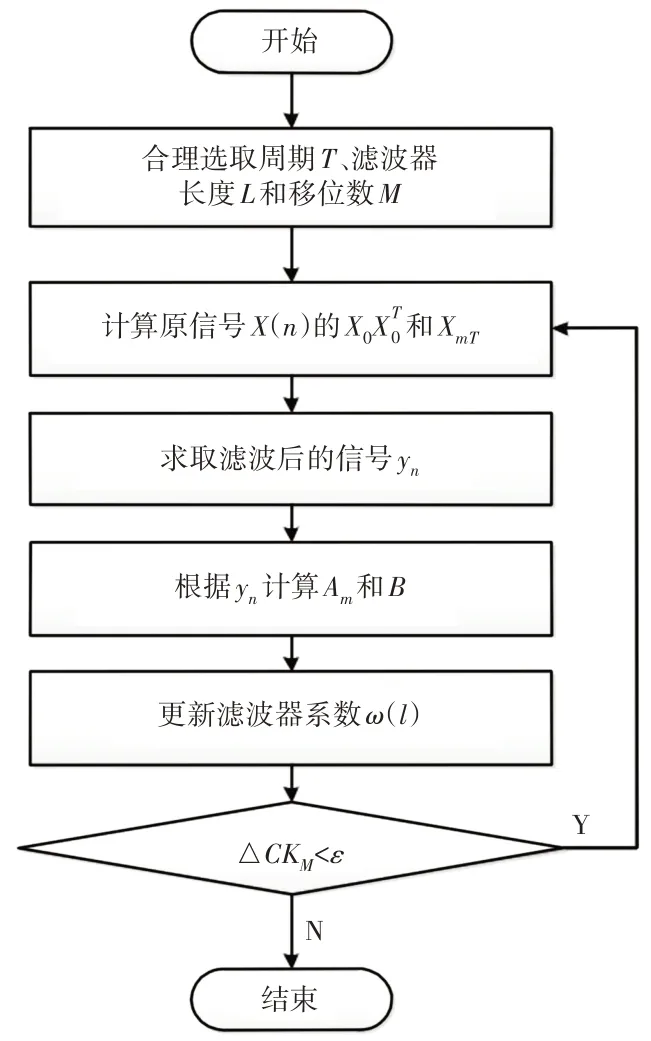
图1 MCKD算法流程图Fig.1 MCKD Algorithm Flow Chart
2.2 迭代滤波
IF分解算法应用迭代提取的思想来提取IMF。IF能够自适应地把一个复杂信号分解为多个IMF与一个趋势项之和[13]。该方法通过对原信号x(t)滤波构造滑动算子v(x(t))替换EMD方法的中值曲线求解过程。由x(t)和滤波函数ω(t)计算卷积得滑动算子:

ln由下式(4)得:

式中:N—信号的采样点数;k—待分解信号的极值点数;λϵ[ 1,3 ],λ是一个调优参数,取决于原信号的信噪比,信噪比越高,λ的取值就越大,通常固定在1.6左右[14]将一个正数舍入接近于零的最近的整数。
波动算子为:

满足迭代停止条件的波动算子μ(x(t))为IMF1,否则继续迭代。

式中:μi,n—第i次筛选得到的波动算子。过程如下:
(1)由式(3)得出滑动算子v(x(t))。
(2)由信号x(t)和式(4)计算滤波区间ln。
(3)由原信号x(t)与IMF1的差得:

以r1(t)为原信号,循环(1)~(3)过程,筛选出第2个IMF分量IMF2,重复m次迭代得n个符合要求的IMF分量(m≥n)。当剩余信号rn(t)具有趋势分量状态时,IF算法迭代结束。

2.3 自适应局部迭代滤波
ALIF方ALIF与现有的IF算法有两个主要方面的不同,一是ALIF 利用Fokker−Planck 微分方程构造具有紧支撑的光滑低通滤波器(FP 滤波器);二是根据信号本身逐点调整滤波器长度。弥补了固定的滤波函数自适应差、函数波形失真等问题。

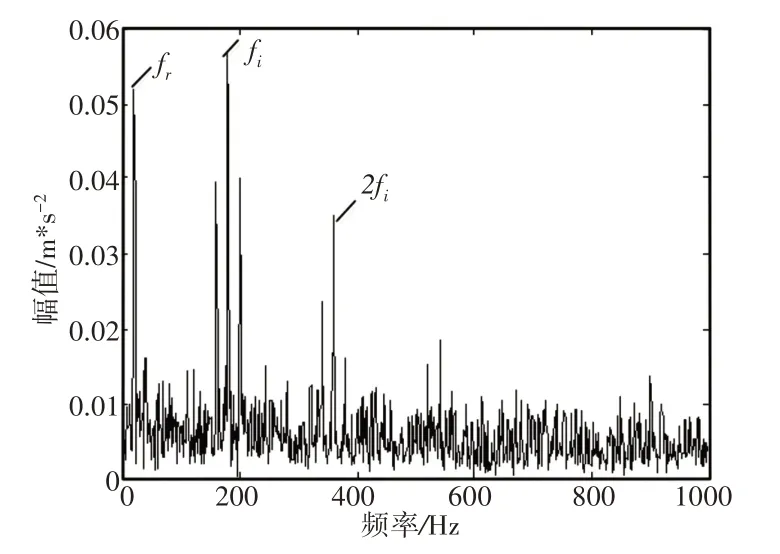
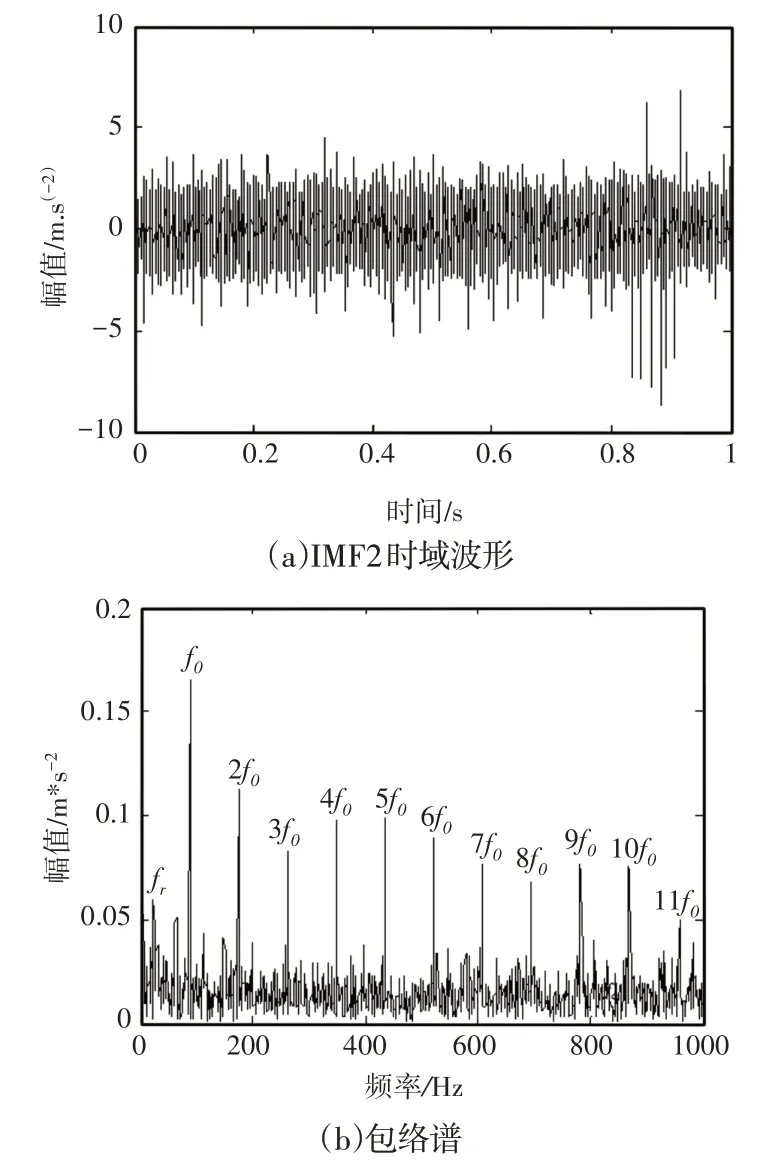
式中:h(x)和g(x)—光滑可导函数,且在[a,b]( 其中,a<0 式中:−α(h(x)p)x使Pt从端点a和b的两端向(a,b)的中心聚拢,同时,β(g2(x)p)xx从区间(a,b)的中心向两端点a、b移动。当两者达到平衡时有: 此时存在方程的解Pt满足: (1)∀xϵ(a,b),有p(x)≥0; (2)∀x∉(a,b),有p(x)=0; 方程的解全部都在区间(a,b)内,即滤波器函数ω(t)就是Fokker−Planck方程Pt的解。 由(a,b)的取不同的值,滤波器ω(t)就有不同的形状,从而实现ALIF方法对滤波函数的自适应。 (1)采用AMCKD对轴承振动信号降噪。MCKD降噪的关键在于滤波器长度L和位移数M的选择,M太小会导致在时域上冲击信号不均匀分配的问题,M太大会加大计算量,且易导致漂移,根据经验,M的范围为(3~8)。采用文献[15]提出的步长搜寻法,根据信号排列熵值越大,信号中高频冲击成分越多,信号复杂程度增加的原理对滤波器长度L和位移数M两个参数寻优。 (2)采用ALIF 算法分解经降噪处理后的信号,得到多个IMFs分量。 (3)求取每一个IMF分量的峭度值,依据峭度最大原则,挑选出峭度值最大的敏感IMF分量,对得到的敏感分量IMF进行Hil‐bert包络谱分析,算法流程图,如图2所示。即可从谱图中准确的识别滚动轴承故障特征频率。 图2 AMCKD−ALIF方法流程图Fig.2 AMCKD−ALIF Method Flow Chart 滚动轴承故障信号通常具有非线性和非平稳特性,包含大量的故障分量和噪声分量。根据Randall 提出的轴承故障仿真模型[16]。构建轴承故障仿真信号如下: 式中:s(t)—周期冲击分量;A0—谐振强度;fr—调制频率;φA,φω和CA可以是任意常数;C—衰减系数;T定义为两次冲击之间的平均时间T=1/fp;fp—故障特征频率;fn—滚动轴承系统的固有频率;fr—轴承的旋转频率;n(t)—高斯的白噪声分量。 各参数,如表1所示。采样频率设为20KHz,高斯白噪声方差为6,信号信噪比为−9.5。 表1 内圈故障模拟信号的参数Tab1.Parameters of the Inner Loop Fault Analog Signal 冲击仿真信号s(t)时域,如图3(a)所示。经加噪处理后的时域波形,如图3(b)所示。 由于高斯白噪声的干扰,x(t)中周期性冲击信号并不凸出。对仿真信号x(t)进行Hilbert 变换,从图3(c)包络谱中仅能清晰的看出信号的转频fr和内圈故障特征频率fi。 图3 轴承内圈故障仿真信号Fig.3 Bearing Inner Ring Fault Simulation Signal 对模拟的时间序列进行ALIF分解得到前6阶IMF1~IMF6的时域波形(见图4)并计算各IMF分量的峭度值,如图5所示。由图中可以看出经过ALIF处理后,在IMF2处峭度最大,依据峭度值最大准则对IMF2分量进行包络谱分析,结果,如图6所示。从包络谱中看出ALIF算法对信号具有一定程度降噪效果,信号的转频和故障频率fi的1倍频和2倍频比图3(c)更显著,可以清晰的看出2倍频的边频。 图4 仿真信号ALIF分解IMF1~IMF6Fig.4 Simulation Signal ALIF Decomposition IMF1~IMF6 图5 ALIF分解后IMF1~IMF6的峭度值Fig.5 The Kurtosis Value of IMF1~IMF6 After ALIF Decomposition 图6 IMF2包络谱Fig.6 IMF2 Envelope Spectrum 对模拟的时间序列进行AMCKD降噪处理,然后对降噪后的滚动轴承信号进行ALIF 分解,得的一组模式分量并计算IMF1~IMF6的峭度值,如图7所示。依据峭度值最大准则取IMF2作为敏感分量,如图8所示。在图9中的包络谱非常清晰的可看出轴承的转频fr和内圈故障频率的fi及其(2~5)倍频,故障特征被很好地提取出来;相比于图3与图6,AMCKD−ALIF 算法使强噪声信号的冲击成分变的更加突出,对噪声的抑制效果更加显著。因此,相比于ALIF方法,算法更能有效地提取轴承内圈早期故障特征信息。 图7 仿真信号经过MCKD降噪后的ALIF分解结果Fig.7 The Decomposition Result by ALIF of the Simulation Signal After MCKD Denoising 图8 ALIF分解后IMF1~IMF6的峭度值Fig.8 The Kurtosis Values of IMF1~IMF6 After ALIF Decomposition 图9 IMF2包络谱Fig.9 IMF2 Envelope Spectrum 为了验证该方法的有效性,对滚动轴承实验系统振动数据进行了分析。实验系统,如图10所示。 图10 滚动轴承试验系统Fig.10 Rolling Bearing Test System 实验装置由0.55kW 交流电机驱动。黄色箭头指向图10中可替换轴承的位置。本试验采用电火花加工方法对可更换轴承外环进行点蚀处理,模拟轴承外环的故障。利用美国CSI2130数据分析仪,对实验台右侧轴承垂直方向的加速度信号进行了采集。故障模拟试验台的参数和故障频率,如表2所示。 表2 实验参数和故障频率Tab.2 Experimental Parameters and Fault Frequency 传感器采集到高速滚动轴承外圈信号的时域波形,如图11(a)所示。 图11 轴承外圈故障信号Fig.11 Bearing Outer Ring Fault Signal 由于噪声干扰,时域图中无法看出周期性冲击信号,图外圈振动信号的包络谱,如图11(b)所示。 图中仅能清晰观察出故障频率fo,其(2~6)倍频周围出现了与故障特征频率无关的成分,不利于轴承故障诊断。 通过AMCKD−ALIF 算法对外圈滚动轴承故障信号进行AMCKD 降噪处理,然后对降噪后的滚动轴承信号进行自适应局部迭代滤波分解,依据最大峭度准则,获得峭度值最大的敏感分量IMF2,经过降噪后轴承外圈故障信号的噪声能量削减,凸显了故障冲击信号。 当对其信号进行包络谱分析时,包络谱幅值必然会降低,轴承外圈时域波形,如图12(a)所示。 图12 轴承外圈故障AMCKD−ALIF分解结果Fig.12 Outer Bearing Fault AMCKD−ALIF Decomposition Results 包络谱,如图12(b)所示。 AMCKD−ALIF 分解得到故障轴承转频和故障外圈频率及其(2~12)的倍频,与外圈故障特征频率一致,相比于图11(b),图12(b)包络谱中可以非常清晰的观察到转频及轴承的外圈故障特征频率及其各阶倍频,各阶倍频处无明显干扰频率,AMCKD−ALIF 能非常准确的对故障特征频率进行识别提取。 (1)通过自适应MCKD 对滚动轴承信号降噪,可以有效地提取信号中被噪声淹没的周期冲击成分,提升原始信号的峭度,突出信号中高频信息。 (2)对预处理后的轴承信号进行自适应局部迭代滤波(ALIF)分解并提取敏感分量,利用包络谱分析提取故障特征频率。 (3)自适应MCKD与ALIF方法能够准确的诊断提取轴承的早期故障特征信息。 对轴承故障特征提取、故障诊断相关领域的研究具有一定的参考价值。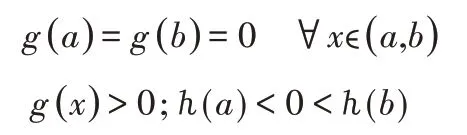

3 AMCKD−ALIF的轴承故障诊断方法

4 仿真信号分析








5 试验分析



6 结论
