基于FPGA 的超声动态聚焦延时参数压缩算法

王 平，梁家祺

（重庆大学电气工程学院，重庆 400044）

0 引言

传统超声成像通常采用延时叠加（Delay and Sum，DAS）的波束形成算法进行成像。DAS 算法原理简单且易于在硬件上实现，被广泛用于医疗诊断的实时成像[1]。同时，随着现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）技术的发展，有学者开始研究将FPGA 作为超声成像的主控芯片，将延时叠加等运算过程移植到FPGA 上实现[2]。在文献[3]中，KIDAV 提出了一种在FPGA上利用流水线处理回波数据最终实现超声实时成像的方案，但是在该方案中，对回波信号的聚焦处理采用的是定点聚焦方法，导致成像结果在焦点附近较为清晰，在远离焦点的边缘区域分辨率却严重下降，此外，该方案在近场处会产生成像盲区，严重影响了近场成像的质量。在文献[4]中，PAI-CHI LI 提出了分段聚焦方案，将扫描区域根据深度分成若干子区间，在每个区间内分别进行定点聚焦，以改善成像质量，但是该方法在近场处仍存在较大误差。在文献[5]中，BOHUMILA提出了动态孔径方案，通过改变对近场聚焦时的孔径大小，有效减小了近场盲区的大小，改善了近场成像的质量。

针对上述文献存在的问题，本文首先介绍超声聚焦的基本原理，之后介绍一种基于误差约束的超声延时参数压缩算法。该算法以逐点聚焦为基础，将聚焦延时参数相近的焦点作为一个分段，段内统一采用一组聚焦延时参数，其本质是分段算法的一种，但是通过在分段边界点的合理选取，使得聚焦延时参数的误差值被控制在一个限定范围之内。在该算法的基础上，本文结合动态孔径技术，在减小近场盲区的同时，进一步压缩聚焦延时参数的存储空间，减少算法的硬件资源需求。

1 超声动态聚焦基本原理

超声聚焦的本质为延时叠加（Delay And Sum，DAS），将各个阵元接收到的回波信号按照焦点到各个阵元之间的声程差进行延时后叠加。叠加后，有效信号相加，噪声信号相抵，从而达到加强焦点处的信号强度和提升信噪比的目的[6]。

动态聚焦是焦点跟随探测深度变化而变化的聚焦方式，各个阵元的延时时间也随焦点变化而改变。在数字动态聚焦系统中，各个阵元的回波信号经A/D（模数转换器）采集之后缓存在随机存取存储器（Random Access Memory，RAM）中，不同深度的回波信息按时间存储在RAM 的不同地址中，深度越深的回波其返回时间越迟，则对应地址值越大[7]。而扫描线上同一点到各个阵元的距离不同，若该点的回波信息在中心阵元对应的RAM 中存储在地址ADDRmid处，则同样是该点的回波信息在边缘阵元对应的RAM 中存储地址为ADDRmid+τ，其中τ即为延时参数。在FPGA 中，只要对超声聚焦参数进行预先存储，再根据扫描深度实时读取聚焦延时参数作为RAM 地址读取的附加值，最后将各个阵元RAM 的读取值相加即可完成数字动态聚焦[8]。然而，该方法下，中心阵元的每个地址值都需要一组配套的聚焦延时参数，存储这些聚焦延时参数需要消耗大量硬件资源。在N阵元线型阵列中，一条扫描线的回波数据需要RAM 深度为D=2（Fend-Fstart）fs/c，其中c为超声波介质声速，fs为采样频率，Fstart为起始聚焦深度，Fend为最大聚焦深度，若每个延时参数消耗2 Bytes 空间，则总共将消耗（2N×D）Bytes 空间，因为对称性减半也还需要（N×D）Bytes 的空间。若想减少资源消耗，则需要对聚焦延时参数进行压缩，使用时再实时解压输出，因此聚焦延时参数的压缩算法是能否在FPGA上实现动态聚焦的关键。

2 基于误差约束的超声延时参数压缩算法

本节将简单介绍一种基于误差约束的超声延时参数压缩算法。在N阵元阵列中，阵元分别编号0，…，N-1，阵元间距d，探测深度区间为[Fstart，Fend]，则区间内一点Fk做焦点时其到阵元i的延时时间ti,Fk为：

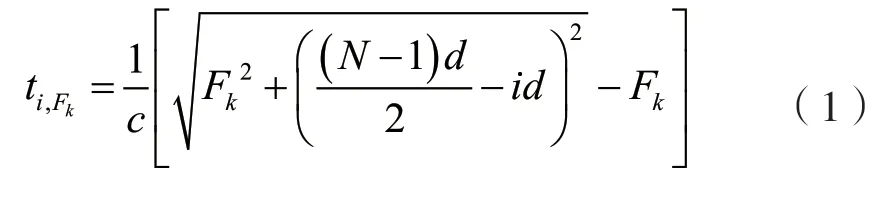
在该分段方法下，在任意一段聚焦区域[Fk，Fk+1]内，聚焦延时时间的变化量绝对值小于1/fs，各个通道的聚焦延时参数的递减量DECi，k只存在“ 0 ”和“ 1 ”两种情况，则各个通道在进入第k组分段时，其聚焦延时参数可表示为

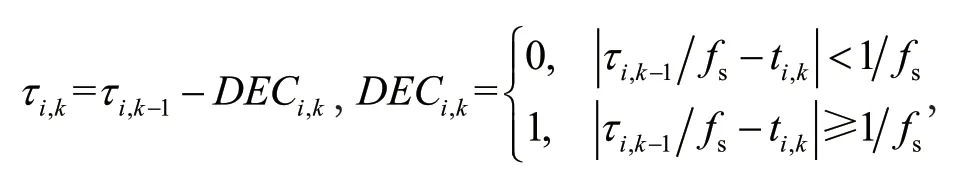
τi,0为各个通道聚焦延时参数的初始值，可通过式（4）进行计算：

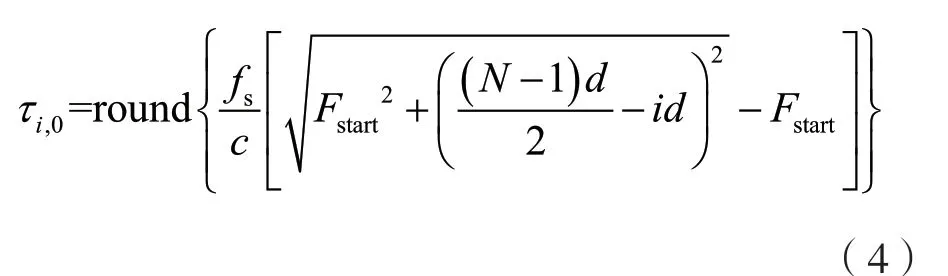
此时，只需要记录上述ADDRedge,k，DECi,k和τi,0三种信息，即可通过简单加减运算还原出所有聚焦延时参数。每个ADDRedge,k值占用2 Bytes 存储空间，数量为K；每个DECi,k值占用1 bit 存储空间，数量由于对称性减半为KN/2；每个τi,0值占用2 Bytes 存储空间，数量由于对称性减半为N/2。综上所述，压缩后的聚焦延时参数总计占用存储空间为（N+2K+KN/16）Bytes。

拥有自信，能让自身的智慧的灵光得以闪亮，创造出许多自己也意想不到的奇迹。小仲马在自己艰难的创作中并没有困为一时的挫折而放弃，而是凭借着自己的信心和才能去闯出了一番天地。巴鲁玛面临唾手可得的成功放弃了，选择了一条与大相径庭的充满挑战的道路勇敢的走下去，是心烛点亮了她的锦绣人生；也是心烛使她骄傲地面对人生。

3 结合动态孔径的超声延时参数压缩算法

动态孔径技术指随着探测深度改变，激活的阵元数也随之改变，其原理如下文所述。超声相控阵在形成波束时会对不同入射角的回波信号产生不同强度的响应，对于均匀线型排列的相控阵来说，其对不同入射角度θ的响应幅值归一化后的波束方向图可表达为：

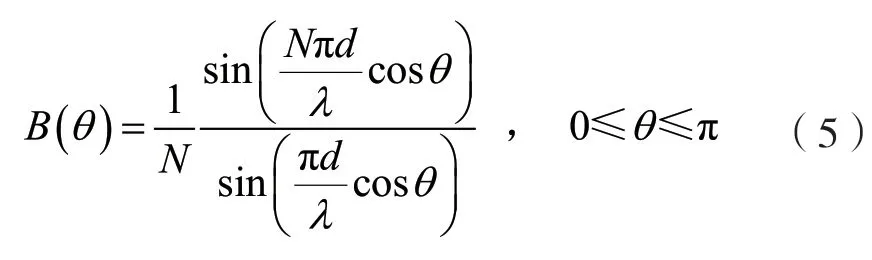
式中：N表示阵元数量，d表示相邻阵元中心距，λ表示入射波波长。其图像如图1 所示。

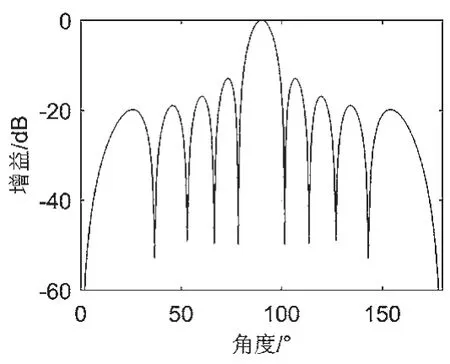
图1 波束方向图

取B=-3 dB 半功率点作为波束区域的边界，则两个半功率点之间的夹角为可视夹角。该角度意味着，不计超声衰减的情况下，在相控阵正前方可视夹角内，若存在一个向周围均匀发散的点震源，则会在该波束上留下一个可视影像，区域外的震源则无法留下可视影像，该扇形区域被称为可视区域。若保持阵元数不变，则相邻的扇形可视区域之间的近场会有一块扇形无法覆盖到的三角形盲区。通过改变N的取值可以改变可视夹角大小，阵元数量越少，孔径越小，对应的可视区域夹角就越大，则相应的相邻两条波束之间的成像盲区就越小。然而，可视区域夹角的增大会引起成像横向分辨率的下降，探测深度越深，横向分辨率下降就越严重，因此孔径大小的设置需要综合考虑对可视区域夹角和横向分辨率的影响。

为了减少近场盲区同时又不影响远场分辨率，可以采用动态孔径技术，即在近场只激活中心区域少量阵元，维持较小孔径，随着聚焦深度的增加，激活的阵元数也逐渐增加，直至增大到所能激活阵元数的最大值。不同探测深度对应的阵元开启数量的具体计算过程如下文所述。

将N=2n（n=1，2，…，Nmax/2）分别代入上述过程求得对应的可视夹角Δθn，则该波束可视区域单侧的边界线可表示为：

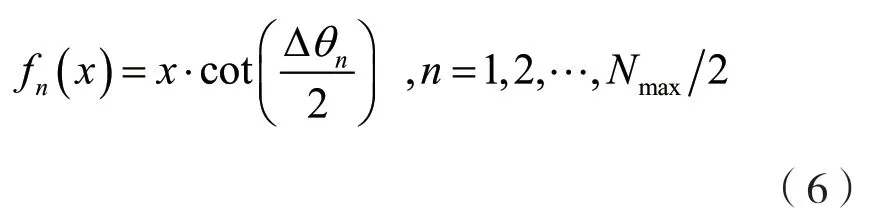
相邻波束中心距为db，一般情况下db=d，现x=db/2 可得一系列fn（db/2）值即为动态孔径分段边界深度。图2 展示了使用动态孔径技术前后的可视区域范围，图2（a）为使用前，图2（b）为使用后，由图可知，采用动态孔径技术之后，近场盲区区域面积将显著减小。

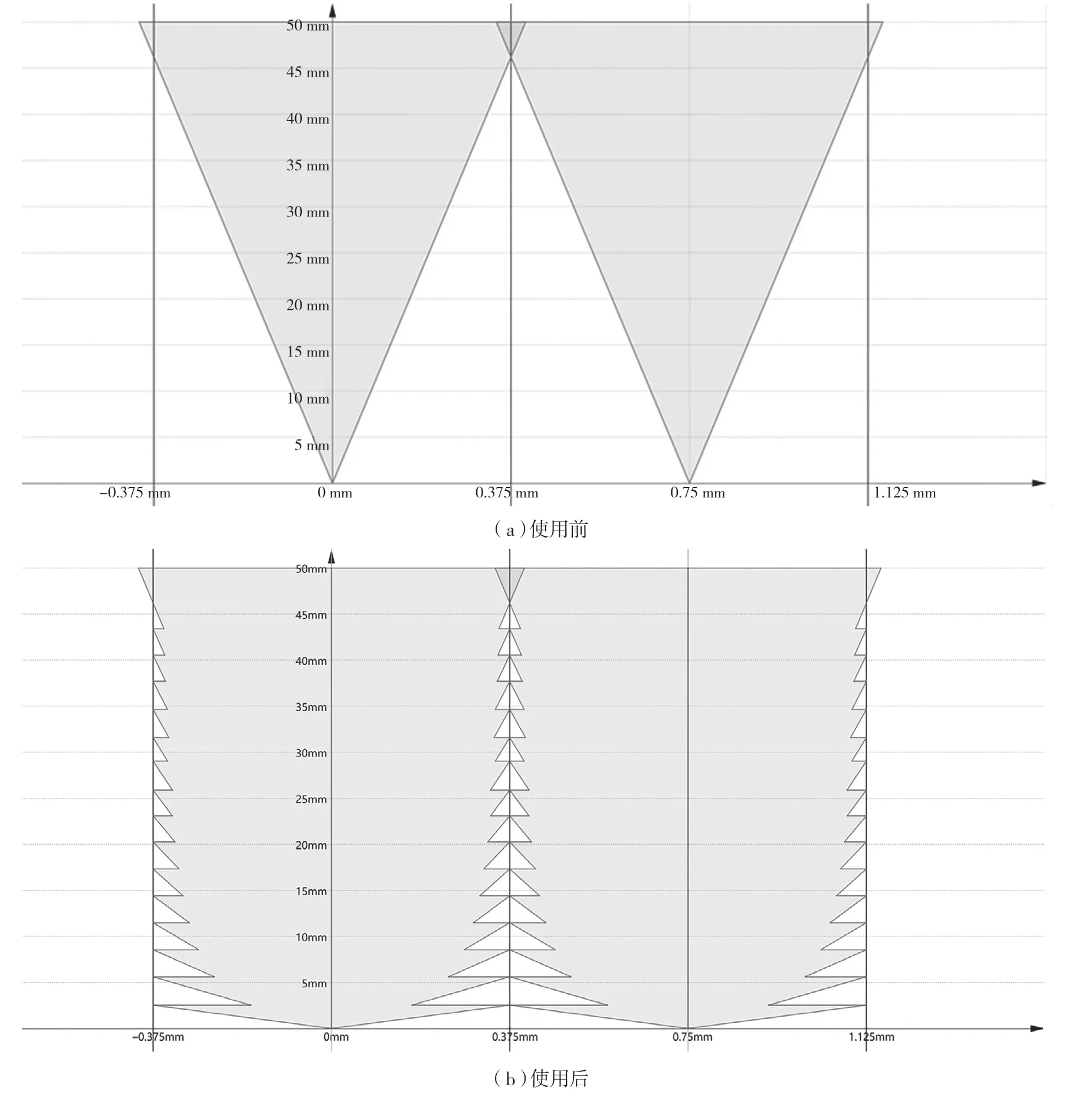
图2 使用动态孔径技术前后的近场可视区域

在第3 节的压缩算法中，算法对探测深度进行了分段，其分段特点为前密后疏，而各个阵元的递减信息中，递减值为“ 1 ”的区域主要集中在边缘阵元。若将动态孔径分段投影到第3 节算法的递减信息中，其结果如图3 所示。

图3 动态孔径分段在聚焦分段递减信息上的投影

图中紫色区块表示该通道在进入该分段时的递减值为“0”，即不发生递减，黄色区块表示递减值为“-1”，红色线段所围成的区域为激活的阵元区域。由图3 可知，在阵元激活区域外，存在大量的“-1 ”递减信息，这些信息由于对应阵元在该分段并未激活，都成了无效信息；而在阵元激活区域内，“-1 ”递减信息变得相对稀疏，存在进一步压缩的可能。

基于上述现象，本文提出一种结合动态孔径的聚焦延时参数分段压缩算法，首先按照上述过程计算出动态孔径分段边界值fn，则整个探测区间[f0,将被划分为Nmax/2 段，在每个子区间内，分别采用基于误差约束的超声延时参数压缩算法计算分段边界地址、激活阵元的递减值和阵元初次激活的初始聚焦延时参数值，即可还原出各个阵元需要的聚焦延时参数值。

该算法下用FPGA 实现动态聚焦和动态孔径的结构如图4 所示。

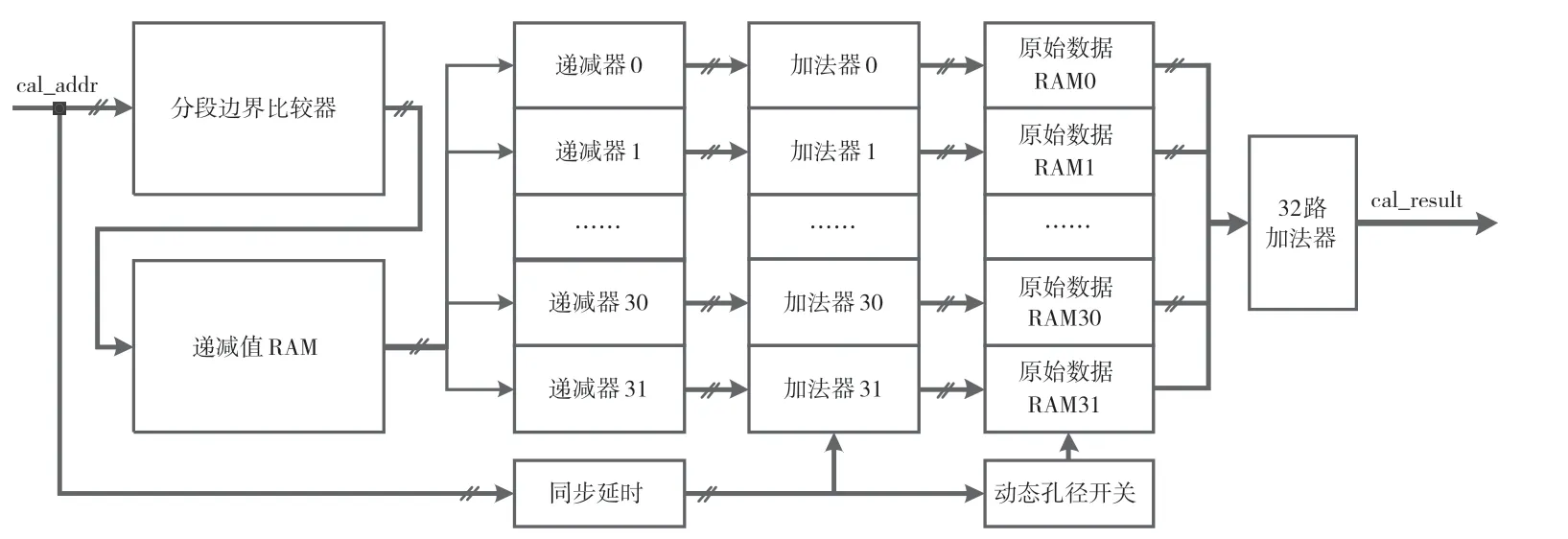
图4 动态聚焦和动态孔径模块的结构示意图

当外围电路发射超声并将回波信号经过A/D采集存储到FPGA 内各个阵元对应的原始数据RAM 后，系统进入波束运算模式。运算开始时，模块外部会使能一个计数器进行加计数，其计数值作为原始数据RAM 读取基础地址值cal_addr 输入模块，在分段边界比较器中和分段边界地址值ADDRedge,k进行比较得到所在分段k，再以k为地址值在递减值RAM 中检索该分段下的递减信息DECi,k传输到各路递减器当中；当cal_addr 值递增跨越ADDRedge,k值时在各路递减器中根据DECi,k值执行一次递减操作，实时得到各通道聚焦延时参数，再将聚焦延时参数和实时的cal_addr 值叠加就是焦点信息在各个通道原始数据RAM 中存储的地址位置，而动态孔径开关会根据该cal_addr 下激活阵元数为各个原始数据RAM 提供读取使能，只有开启的阵元对应的RAM 才能读取出数据；从原始数据RAM 中读取出相同相位的回波数据后，在最后的32 路加法器中叠加，即可得到聚焦结果，整个过程共计产生6 个时钟周期的数据延迟。

4 实验结果与分析

实际应用中，以广东汕头超声电子股份有限公司 的5L128-0.75×10-C58-P-110-2.0-D1型压电换能器探头为例。该探头可同时激活阵元数N=32，阵元中心距d=0.75 mm，声波频率fc=3.5 MHz，介质声速c=1 500 m·s-1，聚焦区间选定在[2，240] mm，采样频率设定为fs=50 MHz。在未采用压缩算法时，缓存一条扫描线的RAM 深度为15 455，则其聚焦延时参数占用的存储空间为N×J=494 560 Bytes，存储压力较大。

使用基于误差约束的超声延时参数压缩算法后，在同样条件下计算可得该算法的分段数K=307，分段序号和探测深度的关系如图5 所示。

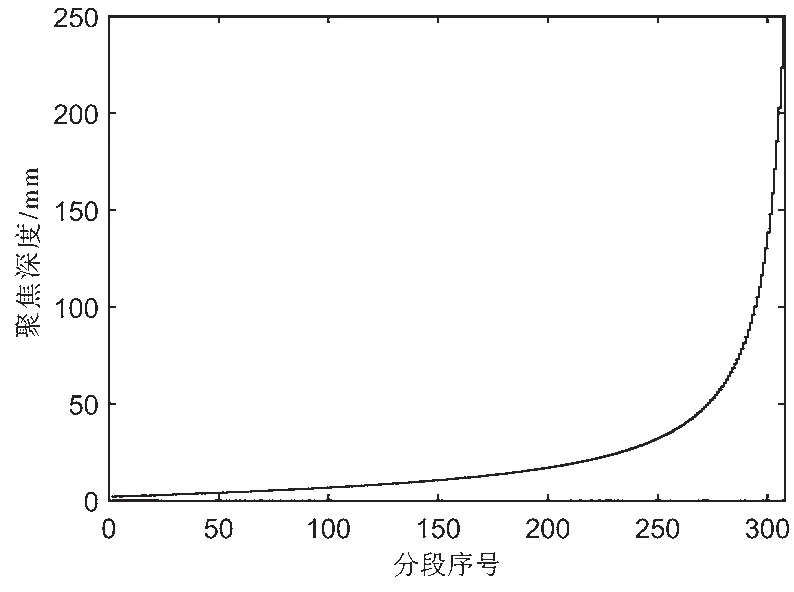
图5 聚焦深度和分段序号关系

该算法下，聚焦延时参数占用的存储空间为（N+2K+KN/16）=1 260 Bytes，压缩率达到了2.548‰，大大节约了对FPGA 硬件资源的使用。根据压缩后的ADDRedge,k、DECi,k和τi,0三种信息，各通道聚焦延时时间还原过程如下。

对于扫描线上探测深度区间内任意一点F，从接收到Fstart处的回波信号开始，对回波信号以采样率fs进行采样并将数据缓存进原始数据RAM 中，则该点F在假想中心通道RAM 中的对应地址为：

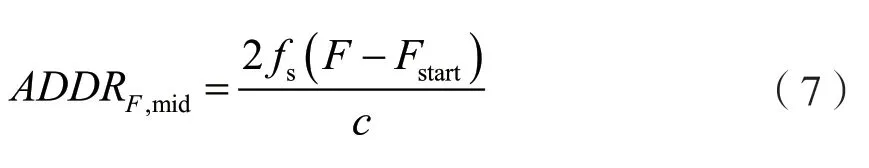
再将ADDRF,mid与各分段边界值进行比较，找到点F所处的分段序号kF，则该点到i号阵元的聚焦延时参数τi,F和聚焦延时时间ti,F分别为：

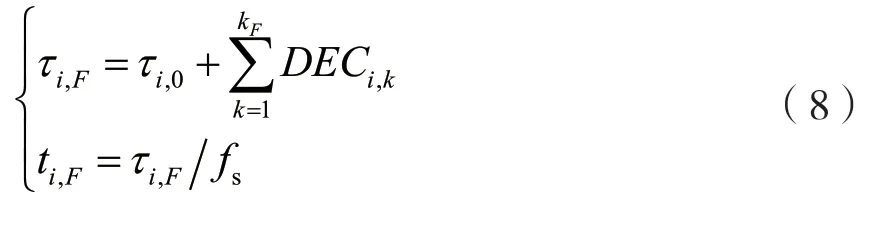
还原后的聚焦延时时间与原始聚焦延时时间的对比如图6 所示，图中自上而下分别为通道1 到通道16 的数据。

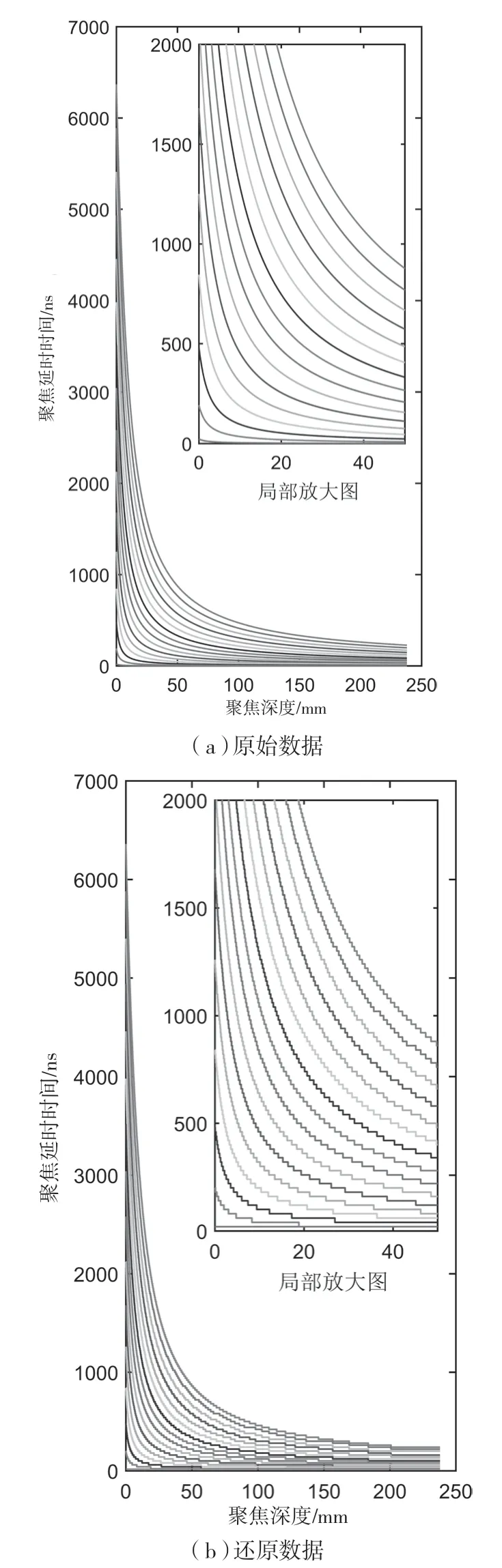
图6 各通道聚焦延时时间

原始数据和还原数据的差值如图7 所示，可得差值在区间[-20，20] ns 之内，符合预设的δ＜fs，误差在可接受范围内。

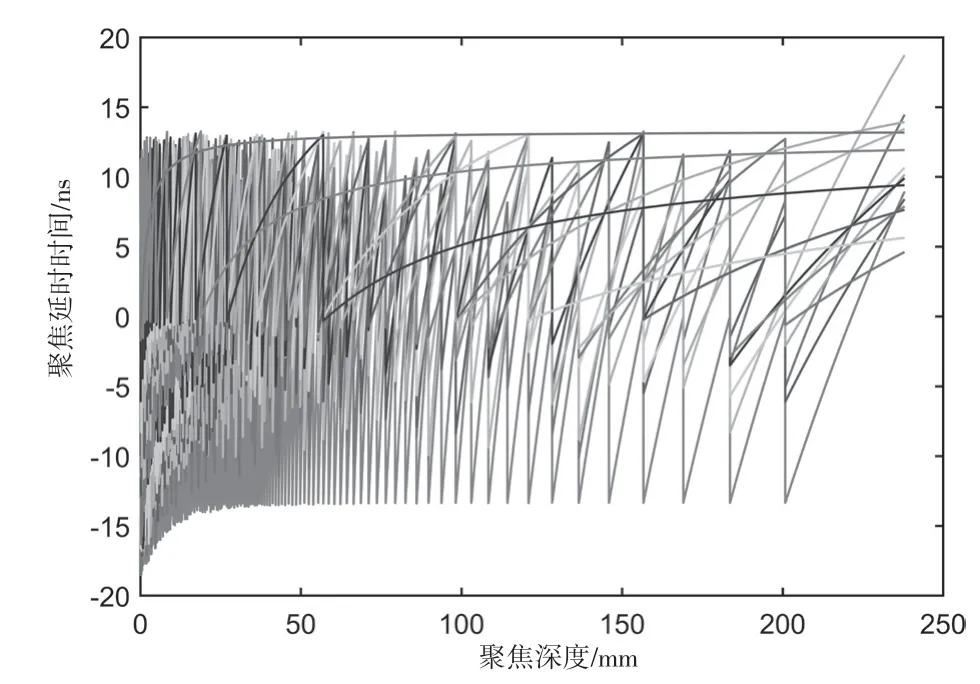
图7 原始数据和还原数据的差值

使用结合动态孔径的超声延时参数压缩算法后，在同样条件下计算可得各个动态孔径子区间的分段数如表1 所示。

由表1 可知，与基于误差约束的超声延时参数压缩算法相比，结合动态孔径的超声延时参数压缩算法分段总数显著减少，从原来的307 段下降到了94 段，同时每个分段中仅需记录已激活阵元的递减情况，所需存储空间将进一步减少。该算法下所需的存储空间如表2 所示。

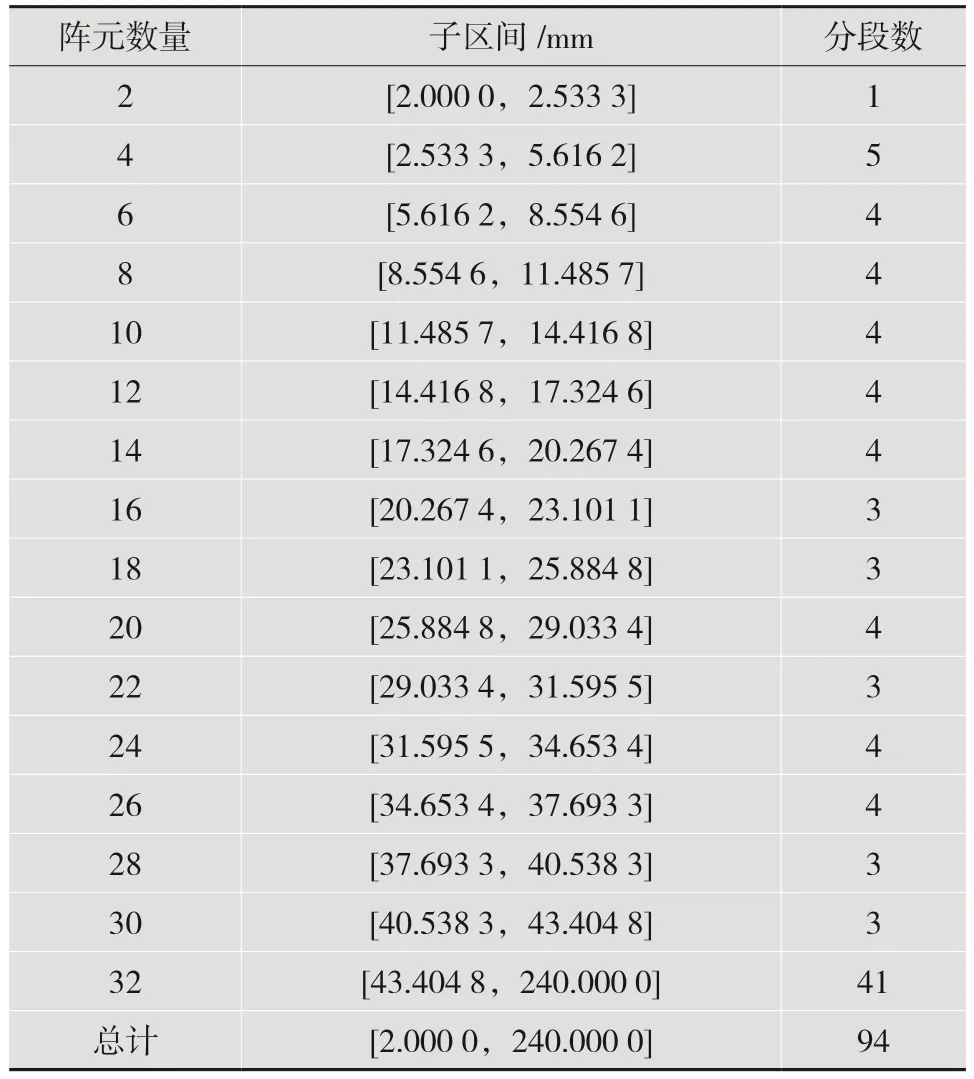
表1 各个子区间分段数

由表2 可知，在之前压缩算法的基础上，结合动态孔径的超声延时参数压缩算法所占用的存储空间再次压缩到了之前的28.15%，是不压缩数据量的0.717‰，极大缓解了聚焦延时参数的存储压力。

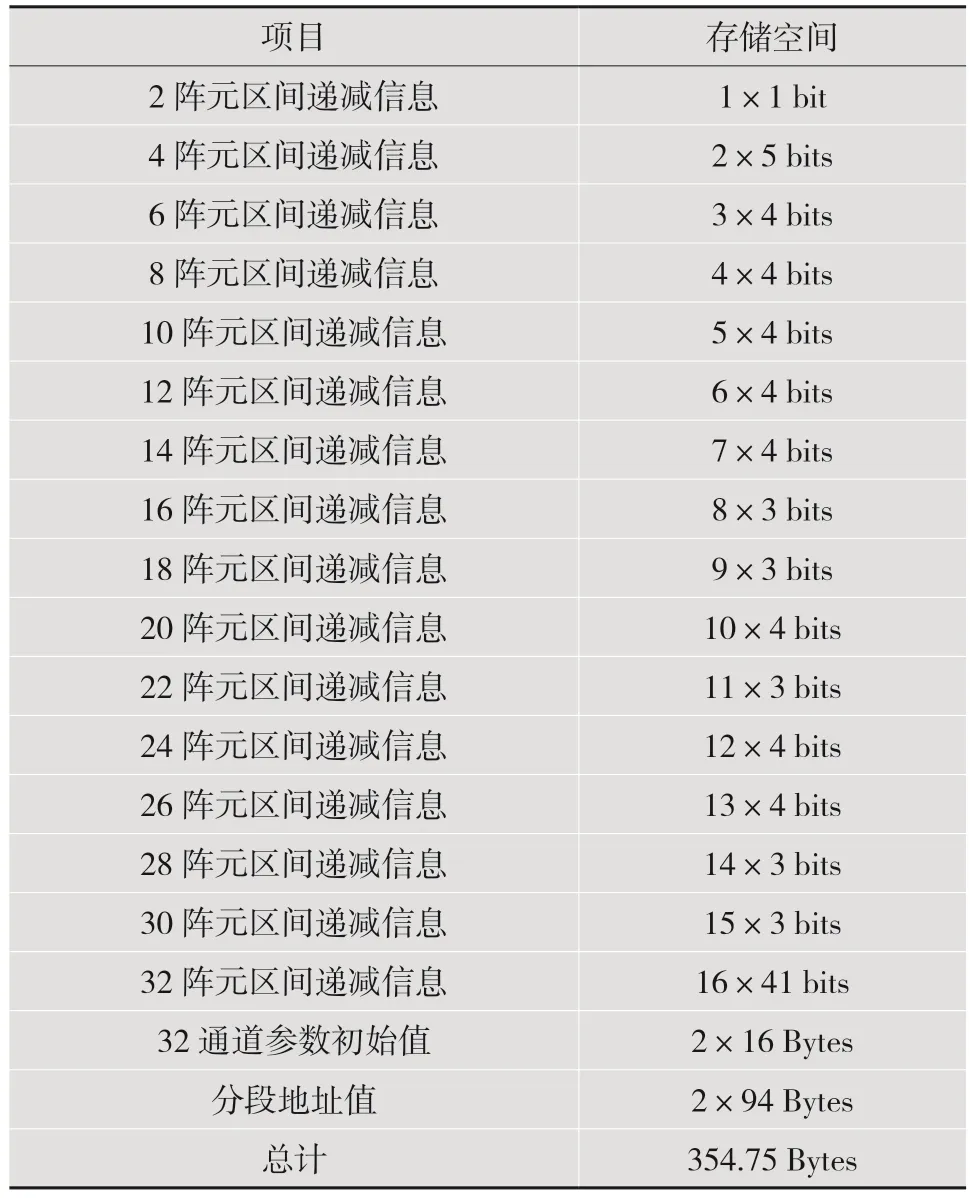
表2 结合动态孔径的超声聚焦压缩算法所需存储空间

5 结语

在实际应用中，以广东汕头超声电子股份有限公司的5L128-0.75×10-C58-P-110-2.0-D1型压电换能器探头为研究对象，存储动态聚焦参数所消耗的空间在不压缩的情况下为494 560 Bytes，采用基于误差约束的超声延时参数压缩算法后消耗的空间为1 260 Bytes，压缩比达到了2.548‰，采用结合动态孔径的超声延时参数压缩算法后消耗的空间为354.75 Bytes，压缩比达到了0.717‰，是第二种压缩算法的28.15%，有效缓解了聚焦延时参数的存储压力，为在FPGA 上实现超声成像提供了理论基础。