降雨对挡土墙黄土边坡长期稳定性影响的模型试验
2022-04-28胡兆江牟海斌张宇鹏李业彤
邹 愈,胡兆江,牟海斌,董 琪,张宇鹏,李业彤
(1.陕西科技控股集团有限责任公司,陕西 西安 710077;2.陕西科控实业发展有限公司,陕西 西安 710054;3.信息产业部电子综合勘察研究院,陕西 西安 710054;4.西安科技大学 建筑与土木工程学院,陕西 西安 710054)
0 引 言
黄土作为由风积搬运作用而形成的第四纪沉积物,具有大孔隙、湿陷性以及水敏性等特征[1-4],极大地影响了黄土边坡的稳定性。为了提高边坡稳定性,通常采用施工工艺简单、工程造价较低的挡土墙作为支挡结构。随着挡土墙服役时间的推进,挡土墙边坡的工程质量受到各类环境因素(降雨、温度、风蚀、行车震动等)的影响下而不断变化,出现诸如墙体倾斜、开裂、鼓胀等病害,影响着边坡工程的长期稳定性影响边坡稳定性的因素中,降雨作用对边坡的稳定性的影响显著[2-3]。
国内外专家学者通过数值模拟、室内试验、数值模拟及现场监测对挡土墙边坡工程的稳定性问题开展研究。肖雁征等从有限元数值计算角度利用特征点对加筋土挡土墙处理滑坡的稳定性进行研究,认为加筋后边坡稳定性得到提高,加筋土挡土墙能有效加固边坡的结论[5];宋鑫华等基于挡土墙的滑移失稳和倾覆失稳等失效模式,运用一次二阶矩法的基本原理,建立涉及到挡土墙高度、填料的内摩擦角等挡土墙稳定性影响因素的非线性功能函数,计算出可靠度指标[6];郑颖人等运用PLAXIS有限元程序对库水作用下坡体内浸润面的位置进行数值模拟,确定浸润面位置进行稳定性分析所存在的误差[7];彭贤清等利用有限元软件ABAQUS通过强度折减法对三维加筋挡土墙进行数值模拟,提出最优土工格室选型[8];赵叶江等依托高填方边坡工程对桩墙复合支挡结构,运用Midas GTS NX有限元软件建立相应的数值模型[9];蒋峰等对高陡边坡进行有限元的二维和三维数值模拟,分析变形发展的规律[10];严秋荣等在无支护和有支护(加设抗滑桩及挡土墙)的条件下开展了降雨对边坡稳定性影响的模型试验研究[11];袁杰等根据相似理论建立试验模型,对比阶梯型直墙结构和阶梯型拱墙结构在不同边坡坡度下的士压力、位移和水压力分布特征[12]。
前人的研究集中在建设期边坡的稳定性分析和评价,对运营期边坡的稳定性研究并不多见,考虑降雨入渗条件下运营期挡土墙边坡的研究更少。笔者选取西北地区运营期典型的挡土墙边坡,开展缩尺模型试验,研究挡土墙黄土边坡的侧向土压力、位移以及水压力随时间的变化规律以及空间分布规律,对长期稳定性进行预测,以期为黄土地区挡土墙边坡质量评价提供依据。
1 试验方案
1.1 试验材料
试验材料来自陕西省延安市宜川县五里坪黄土边坡,为采用砌石重力挡土墙治理的黄土边坡,试验中采用与边坡原型相同的花岗岩石料砌筑挡土墙,石块的平均直径缩小为10~15 cm,弹性模量在6.1~7.4×104MPa(表1)。

表1 基本物理力学指标Table 1 Basic physical and mechanical indexes
1.2 试验设备
试验模型箱1.8 m×2.5 m×1 m,由方形钢管焊接形成箱体框架,两侧为透明有机玻璃,方便观察雨水在坡体中的入渗现象和边坡内部的位移情况;前侧底部30 cm高为一固定的木板,其上钻有小孔以便渗入坡体中的雨水排出,上部1.5 m采用螺栓固定一可拆卸的木板,试验过程中折除木板使坡面临空;底部和背部为固定木板(图1(a))。
降雨设备直径为3 cm,一面钻有直径为1 mm的细孔,一端留进水口,试验过程中进水口与贮水容器相连,通过阀门控制降雨强度大小,雨水从淋雨器上的细孔滴出作用在坡面上,试验开始前需采用量筒校准降雨强度,与实际降雨强度相同(图1(b))。

图1 模型箱和淋雨器Fig.1 Model box and drencher
1.3 试验模型
五里坪黄土边坡原型高8.6 m,挡土墙背垂直,墙面倾角70°,墙顶宽55 cm,墙后填土面为通向坡上的道路,在垂直于挡土墙走向的剖面中墙后填土面水平,墙后填土为第三纪形成的Q3黄土。
试验为1∶10的缩尺模型试验,选用几何尺寸、密度和重力加速度为其本量纲,采用π定理进行相似关系换算,得到各变量的相似关系和相似常数(表2)。
降雨时间相似常数由Terzaghi固结理论计算[26],缩尺模型与边坡原型的几何尺寸不一样,在固定时间内的固结度需一致,因此根据Terzaghi固结理论
TVp=TVm
(1)
TVp为边坡原型固结时间因子;TVm为边坡模型固结时间因子,它们与固结时间的关系可表示为
(2)
(3)
Hp,Hm分别为边坡原型和模型的几何尺寸,CV为固结系数。可得降雨时间的相似比
(4)
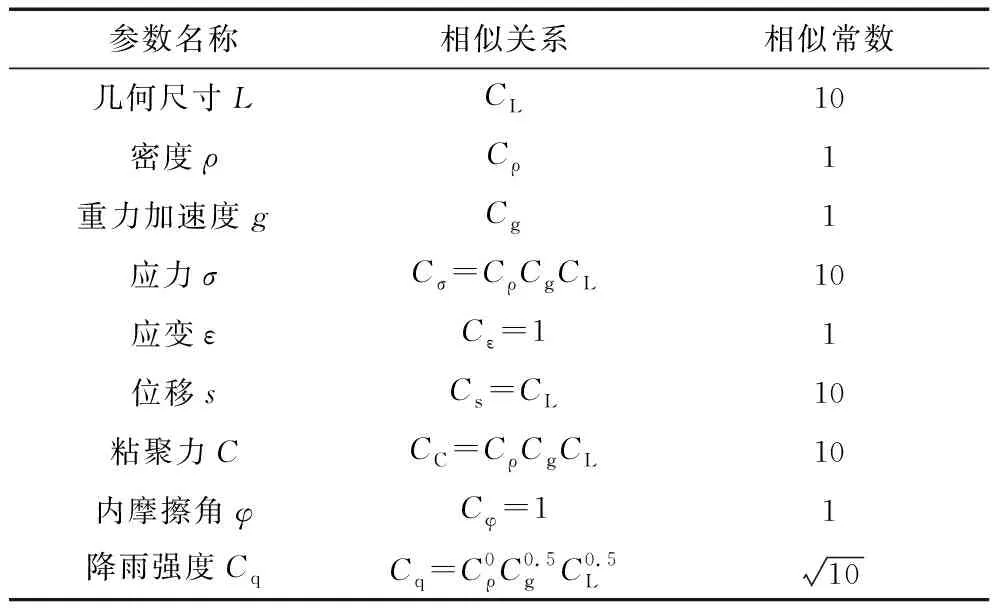
表2 相似关系及相似常数Table 2 Similarity relation and similarity constant
试验几何相似比为Cl=10,时间相似比Ct=100,此边坡原型已建成5 a,模型试验可在0.05 a内完成,即在18 d内完成。
模型填筑采用分层夯填的方法筑成,需将现场采运回的黄土粉碎,然后配制成含水率为19.8%的土样,按每层相同质量的土样填入模型箱并夯实至10 cm,同时采用10~15 cm直径的花岗岩石块砌筑挡土墙,直至夯填到特定高度。通过相似换算边坡模型的高度和挡土墙顶宽度减小了10倍,分别为116 cm和5.5 cm(图2)。

图2 挡土墙治理边坡模型Fig.2 Slope model with retaining wall
1.4 试验数据采集系统
沿挡土墙背竖直向下埋设土压力传感器P1,P2,P3,P4,P5相同,埋深分别为20,40,60,80,100 cm;埋设孔隙水压力传感器U1,U2,U3,U4,U5,埋深分别与P1,P2,P3,P4,P5。土压力传感器和孔隙水压力传感器与应变仪相连,将压力信号转换为数字信号再发送给电脑进行保存。沿挡土墙面中轴线布置5个位移标点,从上向下依次为S1,S2,S3,S4,S5。S1布置在挡土墙肩,S2,S3,S4,S5与S1的竖直距离分别为20,40,60,80 cm(图3)。
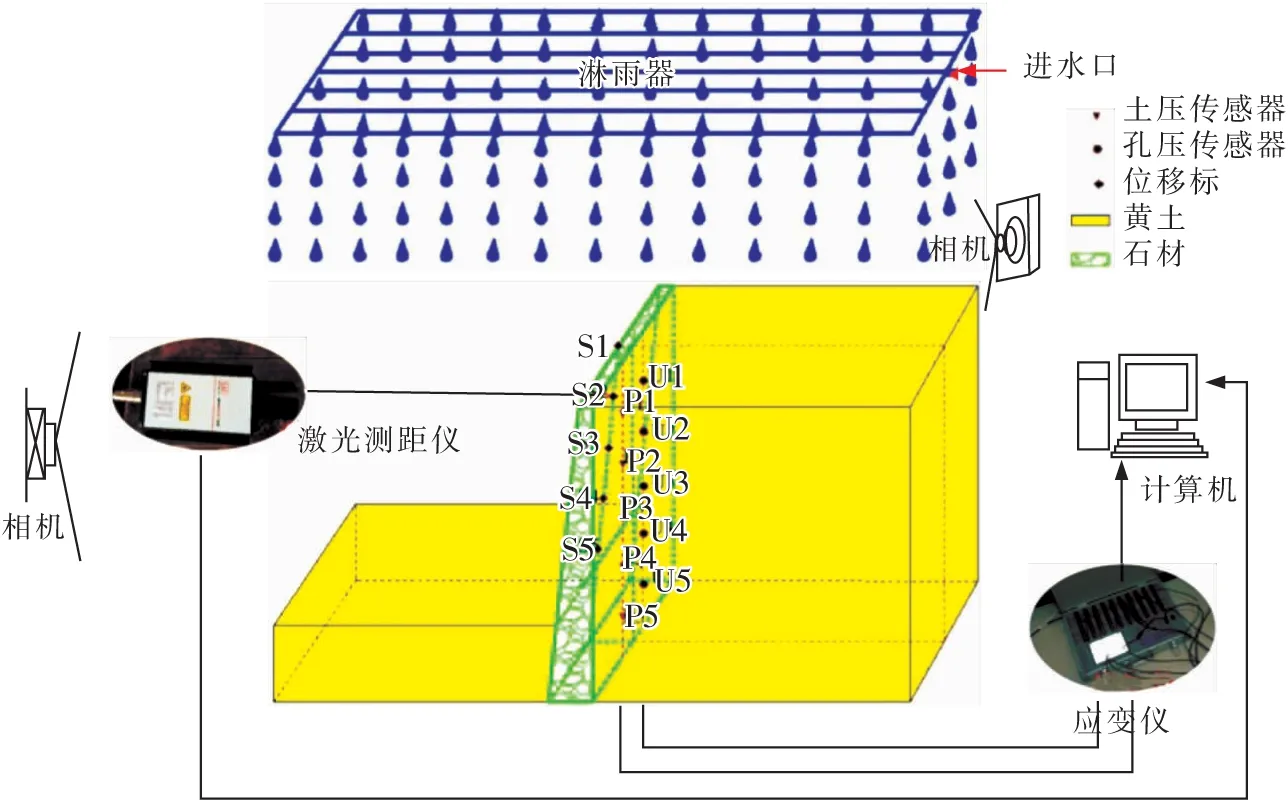
图3 数据采集系统布置Fig.3 Layout of data acquisition system
开启淋雨器进水口阀门,采用量筒在淋雨器下方承接1 min的雨量,与标准的雨量对比,若有偏差调整阀门大小以改变降雨强度大小,直到通过量筒承接的雨水量换算得到的降雨强度恰好与标准降雨强度(36.38 mm/h)相等。将淋雨器加到模型箱顶部,开始降雨试验,同时开启应变仪、计算机数据采集软件,计算机将自动记录试验过程中的土压力和孔隙水压力。试验过程中定时采用激光测距仪测读S1~S5标点的水平位移;并定时采用相机拍摄挡土墙的变形情况。按每次降雨持续2 h,每7.2 h降雨一次,重复3次为每年的降雨过程,试验 86.4 h模拟实际时间1 a,降雨停止的时间为干旱期。重复以上过程5次,模拟边坡在降雨影响下运行5 a。
2 结果与讨论
2.1 孔隙水压力变化
降雨过程中各测点的孔隙水压力除过U5点外均为负值,说明墙背后土体除过底部外均处于非饱和状态。总体上看,各测点的孔压在降雨过程中有一定程度的上升,而雨后其值又迅速地回落,所以表现出在雨季孔隙水压力的激烈波动现象(图4)。
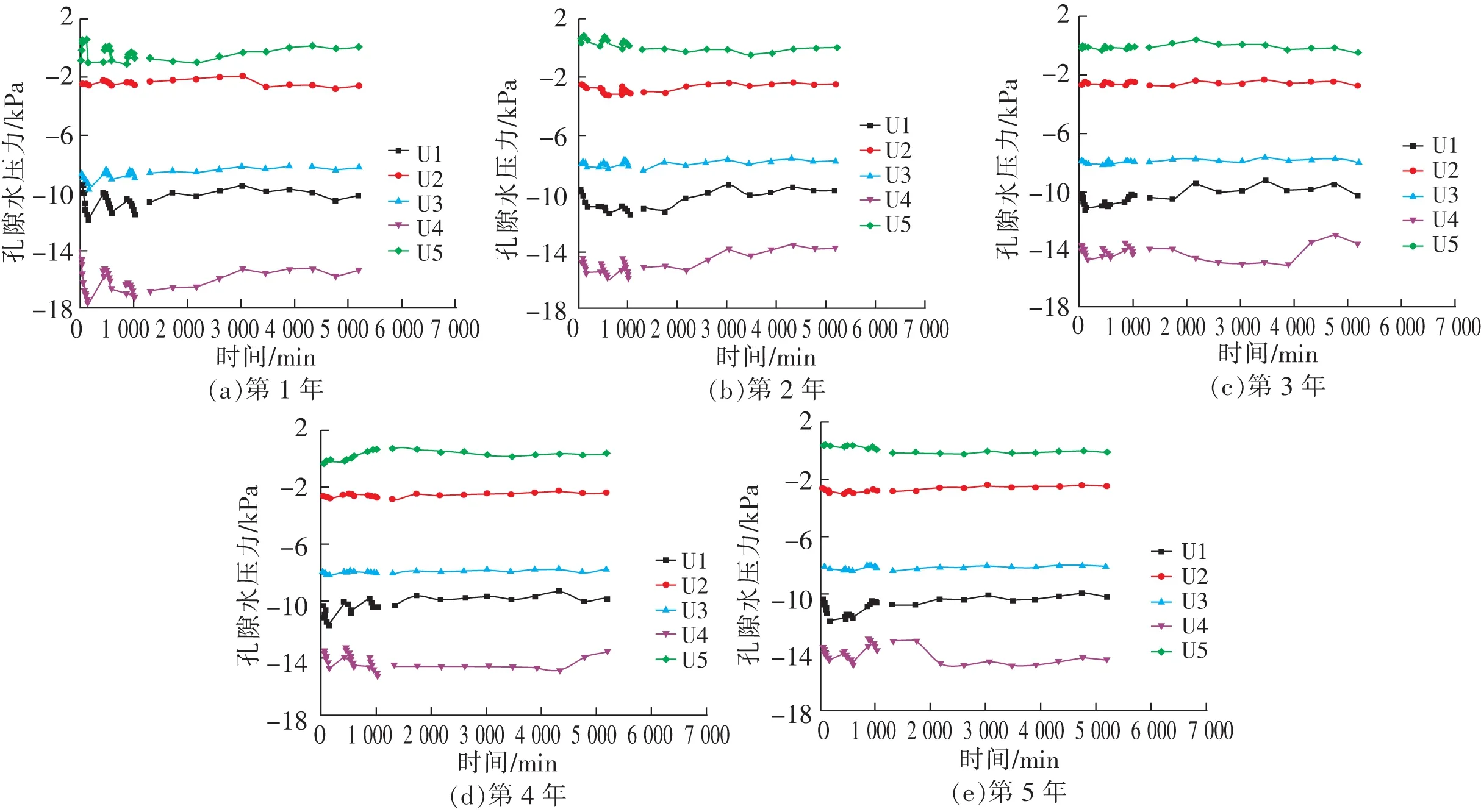
图4 孔隙水压力随时间的变化Fig.4 Variation of pore water pressure with time
U5点处于模型底部以上30 cm处,在整个试验过程中孔隙水压力值由略小于0 kPa上升到0 kPa附近,说明雨水下渗导致模型底部30 cm厚土层饱和,地下水位线位于U5点附近。U4点与U5点距离最近,意味着降雨过程中孔隙水压力值最容易受地下水位影响,所以可以发现在整个过程中其值波动最为激烈,随着降雨循环的进行其值总体上呈现出缓慢的波动性上升的规律,由第1年降雨前的-16 kPa上升到第5年末的-14 kPa左右,意味着雨水下渗使地下水位出现了一定程度的上升。U3点的孔隙水压力在第1年降雨中有一定的波动性上升,从-9 kPa上升到-8 kPa左右,后续的持续时间基本保持稳定不变,说明降雨引起地下水位上升的影响有限,其影响距离只能到U3点的位置,这个距离从地下水位到U3点约为40 cm。而U1、U2点的孔隙水压力在整个过程中只出现一定程度的波动,没有表现出规律性的变化,说明从边坡上部下渗的雨水并没有对这2个点的孔压造成影响,降雨对边坡表层的影响深度也很有限,影响深度不会超过4 m。
降雨影响下表层土体中的孔隙水压力沿深度呈直线增大的规律,但影响深度只有40 cm;40 cm以下到地下水位线附近孔压基本不受降雨的影响,沿深度呈现线性减小的规律,并且地下水位线附近孔隙水压力受降雨影响最明显;而地下水位线以下孔隙水压力沿度又呈线性增大的规律(图5)。
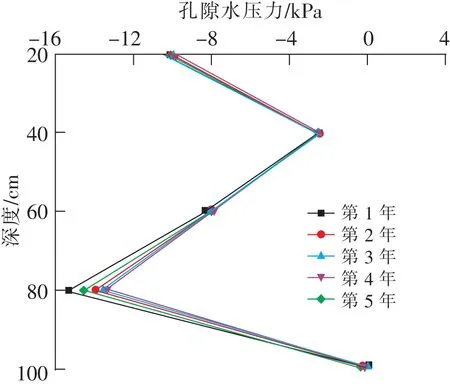
图5 孔隙水压力沿深度的变化Fig.5 Variation of pore water pressure along depth
2.2 墙背土压力变化
第1年P1,P2这2点处的土压力只有剧烈的波动,没有表现出规律性的变化,表明第1年降雨对浅表层墙背土压力产生的影响有限;而P3,P4这2点的土压力表现出缓慢增长的现象,这是由于表层土体由于雨水入渗造成自重增大引起的;而P5点的土压力在第1年降雨中出现了非常明显的减小,其值由1.3 kPa减小至0 kPa,是由于雨水入渗使底部土体软化,导致深层土体中的地应力释放(图6)。
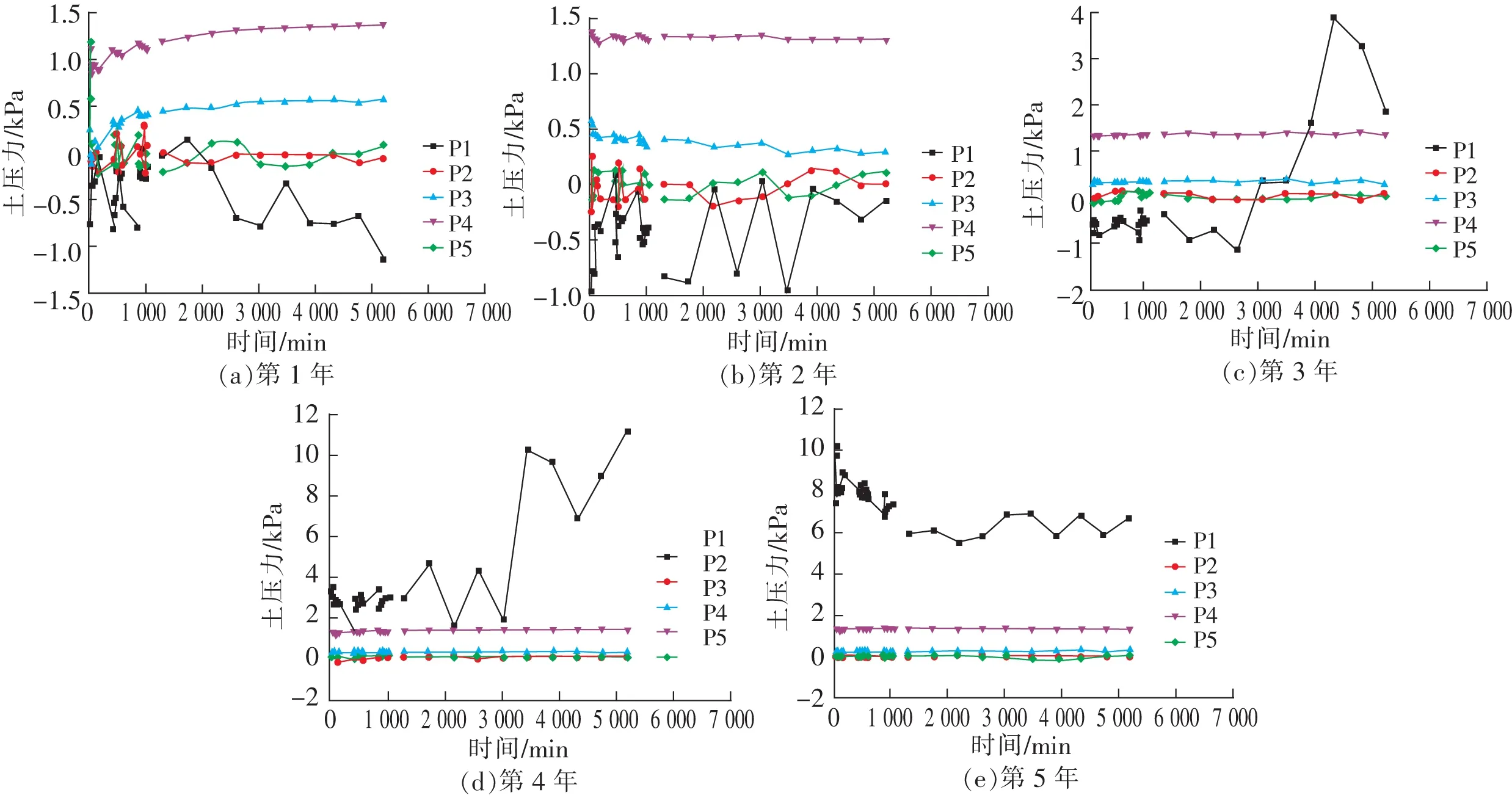
图6 墙背土压力随时间的变化Fig.6 Variation of soil pressure on wall back with time
第2年至第5年只有P1点的土压力出现明显的增减现象,其余各点的土压力处于稳定不变的状态,表明深部土体的土压力在第2年以后不再变化,也说明降雨对边坡深部土压力影响在时域上的有限性。第2年中,P1点的土压力在0 kPa附近波动,认为没有增减;而第3年至第4年中,P1点土力突然出现剧烈增大,由0 kPa增大到12 kPa左右,表明边坡顶部浅层土体在降雨入渗作用下达到了饱和,并向挡土墙背发生了流动,引起土压力剧烈增大。而第5年里,P1点土压力又逐渐回落,这说明挡土墙在墙背土压力作用下向前发生了倾斜,导致顶部土体流变产生的土压力得到了释放,因此表现为P1点土压力在第5年里出现回落。
表层向下20 cm处土压力随时间进行发生了剧烈增大,而下部土层中的土压力变变不明显,说明顶部土体发生了流变,从而出现了墙背土压力在坡脚高程以上随深度表现出顶部和底部大,而中间小的现象,这对坡脚偏上位置处(80cm深处)的墙体产生破坏的危胁(图7)。
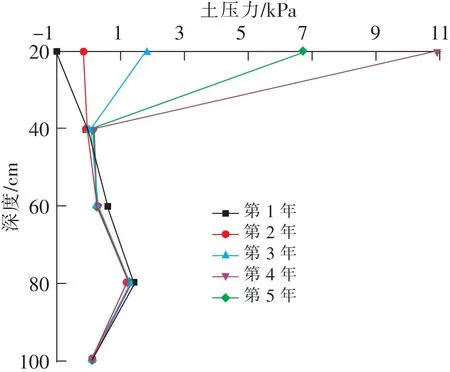
图7 各年末墙背土压力随深度的变化Fig.7 Variation of earth pressure on wall back with depth at the end of each year
2.3 墙面位移变化
降雨中各测点的位移波动剧烈,雨后波动相对平稳;在前3年中特别是第1年中,各测点的位移在降雨中均发生了明显的增大,而第4年和第5年中,各测点位移只有微小的波动,没有发生规律性的增减现象,说明边坡在前3年中处于降雨影响敏感期,第3年后基本处于平稳期(图8)。
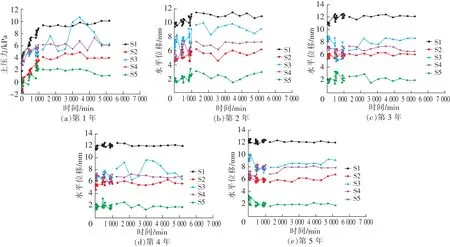
图8 关键点位移随时间的变化Fig.8 Variation of displacement of key points with time
通过对比各测点位移增长过程可发现,挡土墙肩处S1点位移增长最剧烈,第5年末时位移达到12 mm以上,而墙脚处S5点位移增长最微弱,只有2 mm左右,这说明挡土墙在降雨影响下向前发生了一定的倾斜。并且S3,S4点的位移值大于S2点,这说明墙体在S3,S4点还发生一定的凸起现象。
为了更清楚地表现墙体水平位移沿深度的变化,绘制了各年末墙面水平位移沿深度的变化(图9)。墙面水平位移在上部20 cm范围内和下部20 cm范围内表现为线性分布,而在40~60 cm深范围内发生了异常增加,说明墙面在此处发生了挤出性凸起,这正好与边坡原型现调查的破坏现象一致(图10)。这一现象的发生是由于相对单薄的墙体不能抵抗墙背中下部(S3处)较大的土压力,使墙体向前发生了挤出现象,表现为墙面向前凸起。这也给工程设计提出了一个警示,重力式挡土墙在设计中不但要考虑总体的抗滑稳定性,还要特别注意墙体中下部的抗凸起破坏验算。
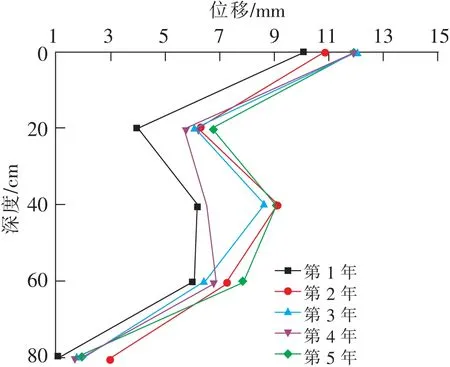
图9 各年末墙体位移随距坡肩垂直距离的变化Fig.9 Variation of wall displacement with vertical distance

图10 边坡挡墙墙面凸起破坏Fig.10 Convex failure of slope prototype
3 结 论
1)降雨入渗对边坡表层土的影响深度不会超过4 m;降雨入渗造成地下水位上升向上的影响距离只有40 cm左右,地下水位线附近的孔隙水压力受降雨影响最明显。
2)降雨影响下,边坡深部土体中的地应力发生释放,造成深部土压力出现减小的现象;而浅表层土体受降雨入渗影响向墙背发生流动,导致浅表部墙背土压力剧烈增大;长期受降雨影响下,挡土墙背土压力沿深度分布表现为顶部和底部大而中间小的规律。
3)挡土墙治理边坡在运行期的前3年,墙面各测点位移有明显的增大,而后续时间里基本不变,前3年挡土墙处于变形活跃期,而后进入相对稳定期。
4)重力式挡土墙设计中不但要关注挡土墙的整体稳定性,还要特别注意墙体中下部的抗凸起破坏验算。
