不同几何和换热条件下转子风阻的变化规律

马 乐，黄宏立，苏开放，梁腾和，张尧立，洪 钢*

(1.厦门大学能源学院,福建 厦门 361102;2.珠海市生产力促进中心,广东 珠海 519000)

近年来，超临界二氧化碳布雷顿循环因具有热效率高、设备紧凑、经济性好和应用前景广等优点成为研究热点.在超临界二氧化碳布雷顿循环系统回路中，涡轮机械是关键部件，其设计研究在超临界二氧化碳布雷顿循环中占有重要的地位[1-4].由于循环系统中的二氧化碳工质会泄漏到涡轮机械的转子-定子腔室内，所以转子在高速旋转时，工质与转子表面的摩擦作用会给转子带来一定风阻损失，使得整个机械的效率降低.风阻损失的能量以热的形式释放到环形间隙中，使得间隙内的温度升高,而高温环境对旋转机械的正常运行有非常大的危害.因此研究转子风阻大小和散热对旋转机械的设计和运行有着重要的意义.

对于同心旋转圆柱体结构，从Taylor[5]指出环形间隙内会出现涡状结构即泰勒涡开始，国内外许多研究者针对转子风阻和间隙内的换热能力进行了研究.Yamada[6-7]经过理论分析后，在低、高雷诺数下分别使用锭子油和水作工质，通过实验测试了不同转子半径和环形间隙宽度对转子摩擦系数的影响，得出了摩擦系数的经验关系式.Bilgen等[8]提出转子摩擦系数是间隙与转子半径比和旋转雷诺数的函数，并通过实验确定转子摩擦系数函数关系中的待定系数，得到了相关的经验关系式.Ren[9]利用数值模拟方法研究轴向流动对转子风阻的影响，得到了没有轴向流动和存在轴向流动时的转子摩擦系数经验公式.梁腾和等[10]利用数值模拟方法研究了转子粗糙高度、转速和气腔间距对转子风阻的影响；该研究侧重转子粗糙高度在中高压、高转速的条件下对转子风阻的影响，在气腔间距与转子半径比值范围为0.025 8～0.103的条件下，气腔间距对转子风阻不会造成明显影响.孙玉昕等[11]利用数值模拟研究同心旋转圆柱体间环形气隙内流体的对流换热情况，得到了不同泰勒数下流场的速度分布、温度分布和热流密度分布，发现环形间隙内的速度分布、温度分布和热流密度分布均与泰勒涡密切相关.Tzeng[12]通过改变转子转速和转子的加热功率，研究同轴旋转圆柱之间的环形间隙中的传热行为，并建立有关离心力、浮力参数与换热系数之间的经验关系式.

转子转速、间隙宽度与转子半径比值以及定子壁面换热条件分别代表影响转子风阻的速度条件、几何条件和热边界条件.之前的研究者在这几个方面做了大量的研究，但是并未对其现象与规律作进一步的解释.本研究从转子转速、间隙宽度与转子半径比值两个方面进行数值模拟，得到转子风阻变化规律，并从环形间隙内部流场泰勒涡的角度对结果进行解释；同时将边界传热和转子风阻进行耦合，研究了定子壁面换热条件对转子风阻的影响，并从热物性的角度对结果进行解释.

1 数值计算模型

1.1 物理模型

涡轮机械转子的损耗发生在转子和定子腔内.本研究针对这一部分进行建模.模型几何结构如图1所示，几何模型抽象成两个同心圆柱体，内圆柱面代表转子外壁面，外圆柱面代表定子内壁面.环形间隙内部充满5 MPa 二氧化碳工质，这一区域即为流体计算域.转子外壁面和定子内壁面均为精抛光后的光滑壁面.

1.2 数值计算方法与网格划分

以5 MPa二氧化碳为工质，在高速旋转的工况下会产生强烈的湍流.由于雷诺应力模型比单方程和双方程模型更加严格地考虑了流线型弯曲、旋涡和张力变化，对于复杂流动有更高的精度预测能力，所以根据所研究的实际工况，湍流模型采用雷诺应力模型.

由于计算域比较规整，本研究采用结构化网格.转子和定子壁面附近的流场比较复杂，因此对定子和转子壁面附近的网格进行了加密.采用壁面函数法处理近壁面流场，Y+值控制在30～200之间，第一层网格高度为0.025 mm，增长率为1.2.将内圆柱面设置为绝热旋转壁面来模拟转子旋转，两侧壁面设置为静止绝热壁面.外圆柱面根据工况条件设置为绝热壁面或对流换热条件下的壁面，其中设置为对流换热时需打开黏性释热选项.所有的壁面都设置为光滑壁面，壁面粗糙高度为0；转子半径和长度分别为25和200 mm.

为了保证计算的准确性，进行网格无关性分析.在间隙宽度为1.5 mm,转子转速为1.8×104r/min的工况下设置径向数量不同的网格层数，通过比较不同径向网格层数下的转子风阻大小来判断是否达到网格无关性的要求.如图2所示，径向网格层数分别设置为15，20，25，30.分析计算结果可得，以径向网格层数为30的模拟计算结果为基准，径向网格层数为25时转子风阻大小的误差不超过1%，满足网格无关性要求，因此下文采用径向网格层数25进行计算.

1.3 计算工况

模拟计算工况如表1所示，在其他条件相同时，分别考察转子转速、定子壁面对流换热系数、间隙宽度与转子半径比值对转子风阻的影响.本研究的计算工况将梁腾和等[10]工况中的最高间隙宽度与转子半径比值由0.103 拓展到0.40，用于分析间隙宽度变化对转子风阻的影响.

2 模型验证

为了验证模拟计算模型对风阻计算的适用性，本研究选取NASA Lewis研究中心Gorland等[13]的实验来进行建模，实验几何模型如图3所示.在模拟计算中，湍流模型为雷诺应力模型.设置10 600，16 608和18 560 r/min 3个工况和实验中的工况相对应，工质物性完全参照实验工质设定.对比实验数据与模拟数据，结果如表2所示.模拟数据和实验数据的误差在±7.14%以内，证明本研究使用的数值计算模型是合适的.

3 结果分析

3.1 转速对转子风阻的影响

间隙内的速度场对转子风阻影响很大.转速大小的变化会导致间隙内部的流动状态发生变化.间隙内的流动通常以Couette雷诺数(Reδ)来描述：

(1)

其中，ρ为密度，μ为流体动力黏度，u1为转子边缘速度，δ为径向间隙宽度.

摩擦系数计算式为：

P=Cfρπω3r14l,

(2)

(3)

其中，P为转子风阻，Cf为摩擦系数,r1为转子半径，ω为转子角速度，l为转子长度.先通过模拟计算得到转子风阻，再通过式(3)计算得到摩擦系数.将工况中的转速换算成Couette雷诺数.如图4所示，转子风阻随着Couette雷诺数的增大而增大，而摩擦系数则随着Couette雷诺数的增大而减小.

图5为速度分布图.其中，计算模型的X方向为轴向，取X=100 mm处径向位置的直线作为特征线.取特征线上的速度及其轴向分速度(u)来分析间隙内部径向的流场变化情况.间隙特征线上速度分布如图5(a)所示，可以看出：靠近转子和定子的边界层有很大的速度梯度，间隙中部的速度大小变化不大；随着转速的增大，间隙内部的速度分布变化不大.在图5(b)中可以看到在间隙内部存在涡状结构即泰勒涡.泰勒涡的强度可以用特征线上的轴向分速度的大小来表示，泰勒涡的强度随着转速的增大而增强.结合图4和5，泰勒涡的强度会影响摩擦系数的大小，且强度越大摩擦系数越小.

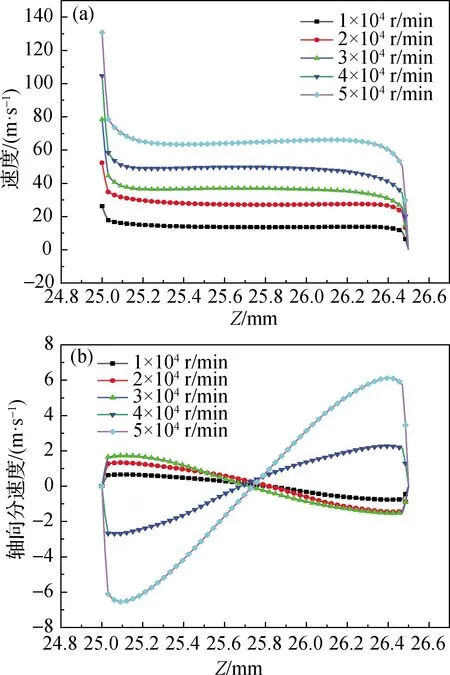
图5 不同转速下特征线上速度(a)和轴向分速度(b)的分布

3.2 间隙宽度与转子半径比值对转子风阻的影响

转子风阻和转子-定子结构的几何条件密切相关.常用间隙宽度与转子半径比值这个无量纲数来表示转子-定子结构的几何条件.

图6为在4×104r/min的转速下，摩擦系数随间隙宽度与转子半径比值的变化曲线.由式(2)可以看到，在转子-定子几何结构和转速相同的条件下，转子风阻只受摩擦系数的影响，此时摩擦系数和转子风阻的变化曲线是一致的.从图6中可见，摩擦系数随着间隙宽度和转子半径比值的增大而先减小后增大，在比值为0.20时摩擦系数达到最小值.

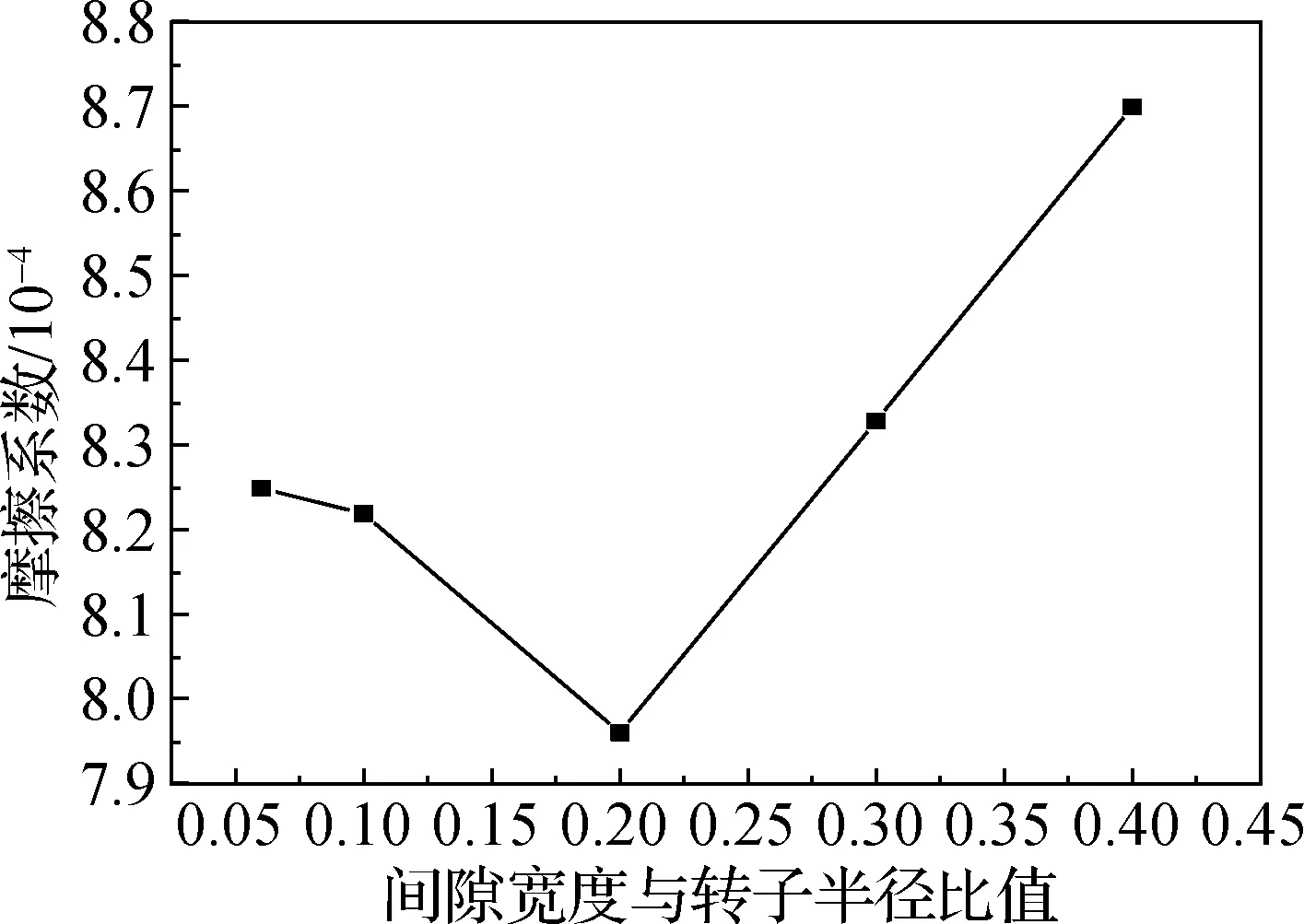
图6 摩擦系数随间隙宽度与转子半径比值的变化曲线

图7为不同间隙宽度与转子半径比值下特征线上轴向分速度的变化曲线，可以看出：随着比值的增大，泰勒涡的强度逐渐增强，在比值为0.20时泰勒涡的强度最大；比值超过0.20后，泰勒涡逐渐不规整，而且泰勒涡的强度也随着比值的增大而减小.由于泰勒涡的强度受转速的影响，研究相同转速工况下泰勒涡的强度对转子风阻的影响更有意义.结合图6和7发现泰勒涡的强度会影响摩擦系数的大小.由于泰勒涡的强度越大，对边界层的搅浑越剧烈，湍流发展得越充分，所以泰勒涡强度越大，摩擦系数越小，转子风阻也就越小.

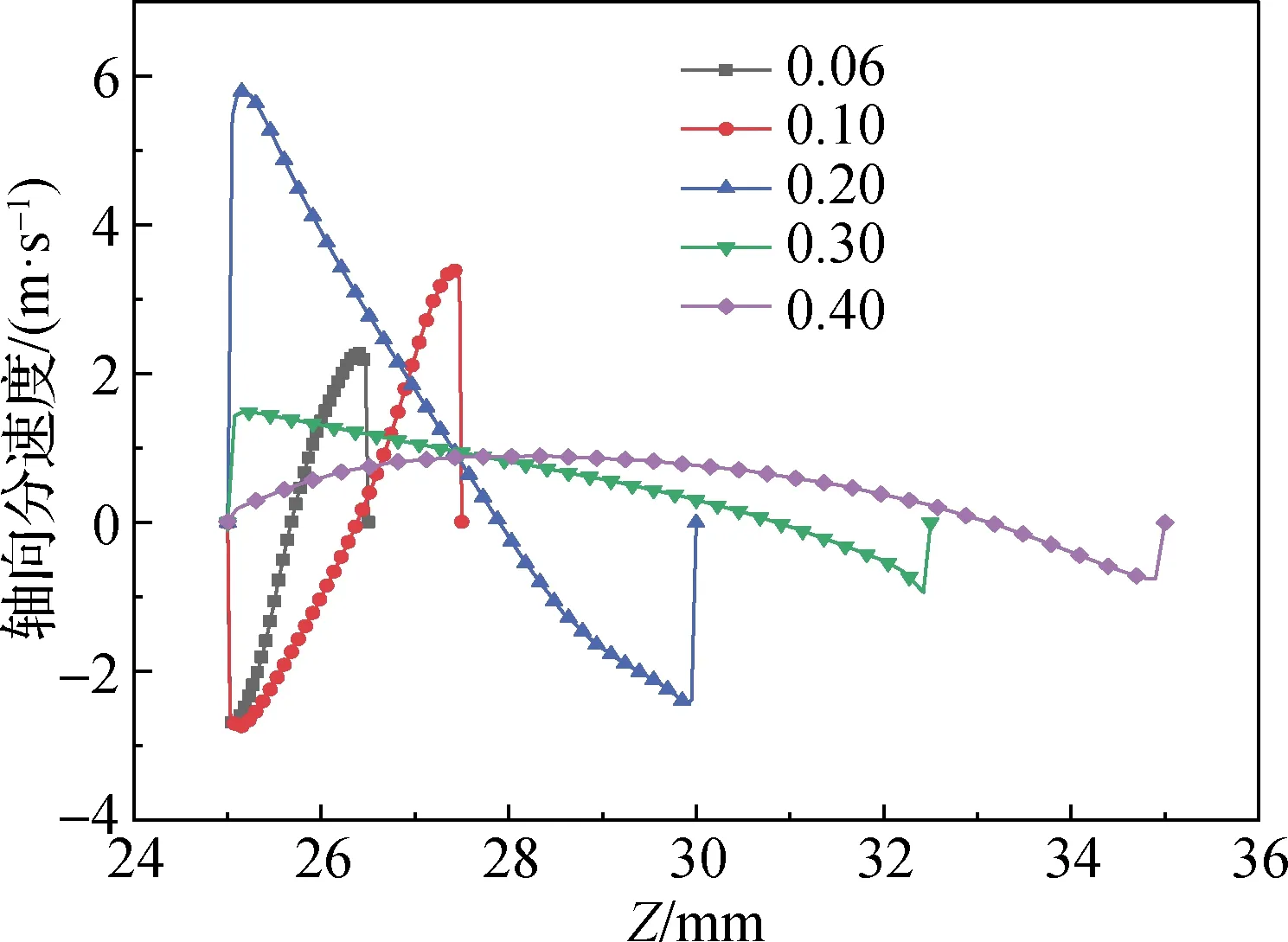
图7 轴向分速度随间隙宽度与转子半径比值的变化

3.3 定子壁面换热系数对转子风阻的影响

转子风阻会以热量的形式传递到转子与定子内部腔室中，导致腔室内部温度上升，而涡轮机械在温度过高的环境下运转是不允许的.因此探究定子壁面换热能力对转子风阻的影响是很有必要的.

图8为转速4×104r/min、初始温度25 ℃的条件下，转子风阻和间隙内平均温度随定子壁面对流换热系数的变化曲线，可以看出，在转子转速一定的情况下，随着定子壁面对流换热系数的增大，转子风阻逐渐增大，间隙内温度逐渐降低.这说明换热条件的改善会使得间隙内的平均温度大大降低，但是转子风阻会升高.

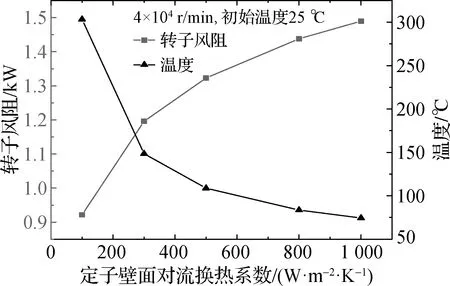
图8 转子风阻和间隙内平均温度随定子壁面对流换热系数的变化

为了探究换热条件影响转子风阻变化的原因，设置了新工况与表1中的工况6～10作对比.为了和前文中的工况作区分，新工况设置为R工况，数字和前文中的工况一一对应，如表3所示.新工况中将表1中工况6～10的对流边界条件设置为绝热边界条件，工质的物性设置为前文工况计算结果下平均温度的物性，再将计算结果和表1中的工况6～10的结果进行对比，结果如表4所示.

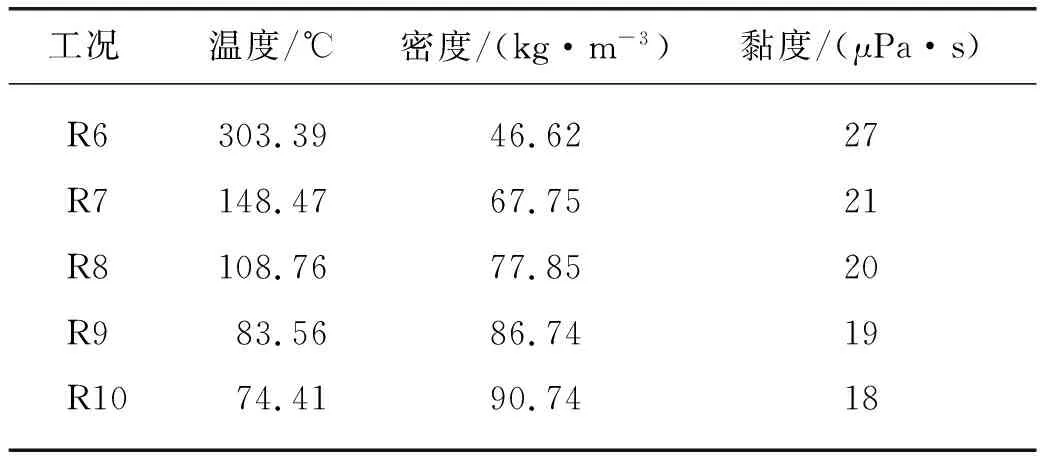
表3 R工况

从表4的对比结果来看，两种情况下结果相差非常小，误差都在2%以内.综上，定子壁面对流换热系数的变化主要引起了环形间隙内温度的变化，温度的变化使得工质热物性参数发生改变，从而导致转子风阻的变化.

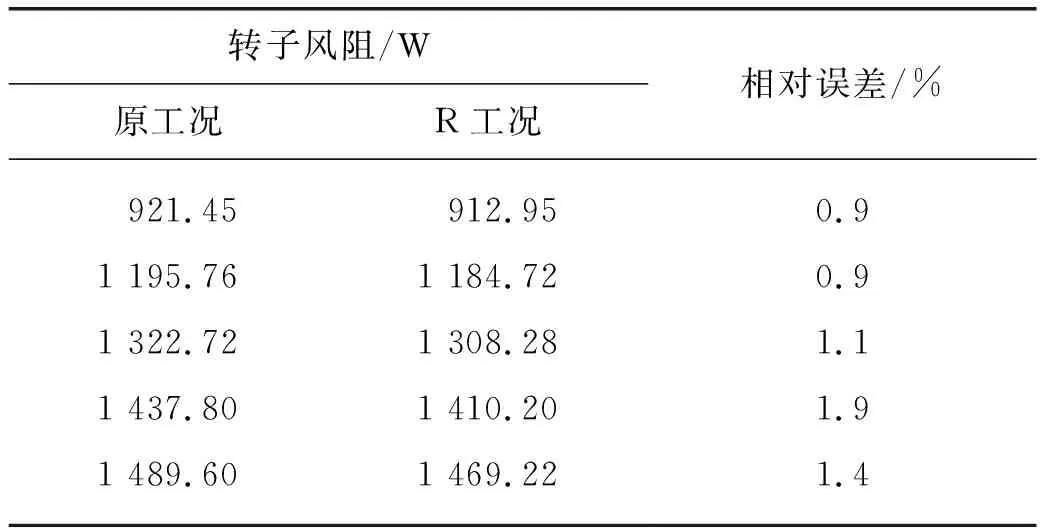
表4 结果对比

4 结 论

本研究以5 MPa、25 ℃下二氧化碳为工质对转子-定子结构进行建模，分析不同转速、不同间隙宽度与转子半径比值以及不同定子壁面换热系数下的转子风阻变化情况，得到以下结论：

1)模拟计算结果和NASA Lewis研究中心Gorland等的实验结果误差不超过±7.14%，说明所采用的数值模拟方法对于转子风阻问题的研究是适用的.

2)在转子-定子结构相同的情况下，转子风阻随着Couette雷诺数的增大而增大，而摩擦系数则随着Couette雷诺数的增大而减小，即转速越高，转子风阻越大，摩擦系数越小，泰勒涡的强度越大.

3)在转速相同的情况下，转子风阻和摩擦系数随着间隙宽度和转子半径比值的增大而先减小后增大，在比值为0.20时达到最小值.

4)转子风阻变化规律可以用泰勒涡的强度来解释，泰勒涡的强度越大，摩擦系数越小.

5)转子风阻随定子壁面对流换热系数的增大而增大.定子壁面对流换热系数的改变主要引起了环形间隙内温度的变化，工质热物性参数随温度的变化导致转子风阻的变化.