单相LCL型程控电流源最优控制策略

陈弈甫，吴一庆，张彦虎

（1.上海电力大学 电子与信息工程学院，上海 201306；2.杭州钱江电气集团股份有限公司，浙江 杭州 311200；3.阳光新能源开发有限公司，安徽 合肥 231600）

常规的开关电流源由全桥逆变器，L型滤波回路构成，适合用于小功率工作场景。但在需求大功率的场景下面临着效率低下，设备笨重等缺点[1]。由于LCL型逆变器的独特优势：（1）高频-60 db衰减；（2）提高滤波效率和效果，适合作为大功率下的输出电流滤波器。而它自身的缺点在于系统阻尼较小，容易在自身谐振频率下产生谐振。

常用的解决方案有以下2类：（1）无源阻尼；（2）有源阻尼。（1）在电容处串联电阻，以提高系统阻尼，但会带来系统损耗；（2）通过控制手段，等效实现增加阻尼的效果，如虚拟阻尼，以及广泛使用的电容电流比例反馈等。有学者通过设计控制器，将电流控制与有源阻尼设计为双环反馈[2]，达到了不错的效果。

也有学者提出将以上两者作为总体来设计的方法。如通过反馈逆变器侧电流（下称I1），电容电压（下称Uc），负载侧电流（下称I2）的全状态反馈解耦策略，实现了dq轴的解耦控制[3]；也有无需增加额外传感器，通过构建隆伯格观测器的全反馈控制策略[4]。而以上策略或是依赖于精确的传感器采样，或是依赖于精确的系统建模。一旦系统长时间运行出现参数漂移或采样发生零点漂移，会极大地影响系统的性能[4-5]。

最优控制理论原先用于航天控制与火箭制导领域的最小燃料损耗问题，而线性二次型控制（LQR）线性二次型高斯控制（LQG）作为一种最优控制，拥有众多优点，有学者研究在并网逆变器下使用基于卡尔曼滤波的LQG控制策略[6]。而在传统工业行业未能获得广泛使用，原因如下：（1）无稳定裕度；（2）无经典控制中极点配置。

本文提出一种基于滑模观测器的LQR与PI复合控制的控制策略，通过配置系统的主导极点，从而保证了系统的稳定性和动态响应性能，而其余极点可动，满足了最优型，并且具有一定的鲁棒性。

1 系统结构

1.1 系统建模与分析

为了分析滤波器对系统的影响，假定逆变器增益kpwm=1；忽略电感和电容上的寄生电阻，根据基尔霍夫电压电流定律，可以得到单相LCL滤波器部分的微分方程：

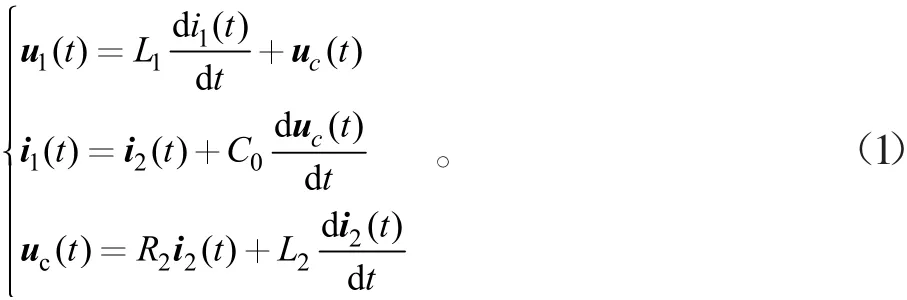
为了实现对电流的精确控制，通过式（2）的广义二阶积分器（SOGI）构建超前90度的正交分量构成两相。

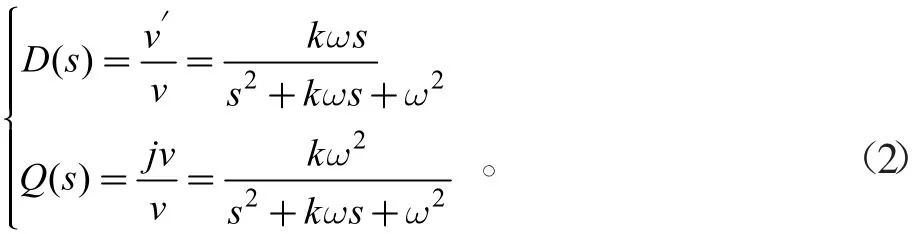
为了兼顾系统滤波和动态响应，工程上K一般取将得到的正交分量与原始量进行旋转变换，便能得到同步旋转坐标系下的微分方程。

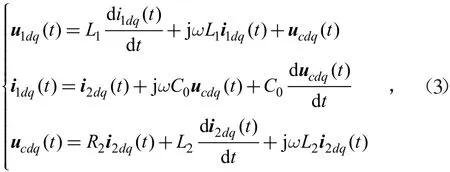
式中，u1dq（t），ucdq（t），u2dq（t），i1dq（t），i2dq（t），分别为dq同步旋转坐标系下逆变器侧电压，电容电压，负载电压，逆变器侧电流和负载电流；w为系统的角频率。

由该微分方程可构建状态空间方程。

其中：

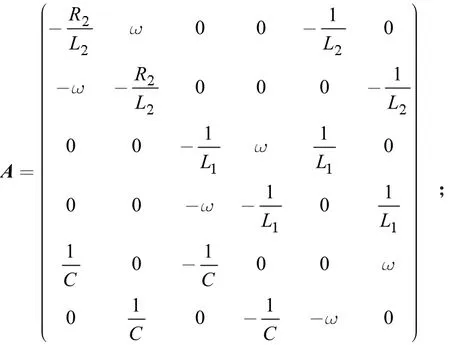
为了在DSP中实现数字控制，需对模型进行离散化，由于采样频率高，可以近似认为采样数值在一个采样间隔内不变，故使用零阶保持器（ZOH）离散。

其中：

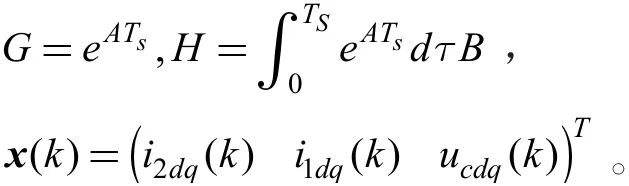
为使建模精确，必须考虑控制器的控制时延。本文采样规则为对称采样规则，周期采样下溢重载；调制方式为单极性倍频调制。

由文献[7]可以得出控制器的时延为Tc，Tc为一个控制周期，则

LQ控制实质上为一种全状态反馈控制，任何常值扰动都会对系统造成稳态误差。而PI调节器由于含有积分环节，根据内模原理可以消除静态误差。将二者联合使用，便能达到期望的动态性能和无静差。

其中：

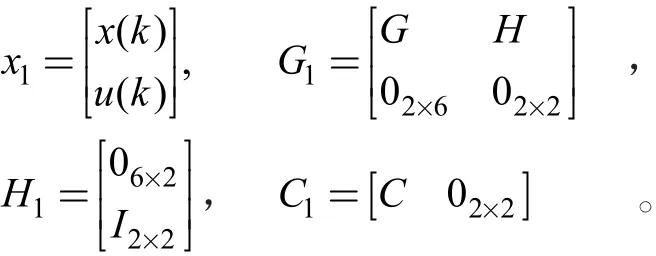
对以上模型分析，可得为了研究电流源的带载能力，将电阻R2按照0.01Ω至100Ω，每隔10Ω一次绘制离散域零极点图，如图1所示。其中：引入一拍延时的一对极点始终位于圆心，不随阻值的增加而变化；LCL滤波器自身固有的极点3对，在电流源轻载时靠近单位圆，容易引发电流环震荡；随着阻值的增加，单位圆实轴上的一对极点逐渐向圆心运动，但剩下的2对极点的运动轨迹如图1所示，最终将回到单位圆附近。故必须采用阻尼控制手段，让系统的极点配置在适合的位置，满足电流源的性能指标。

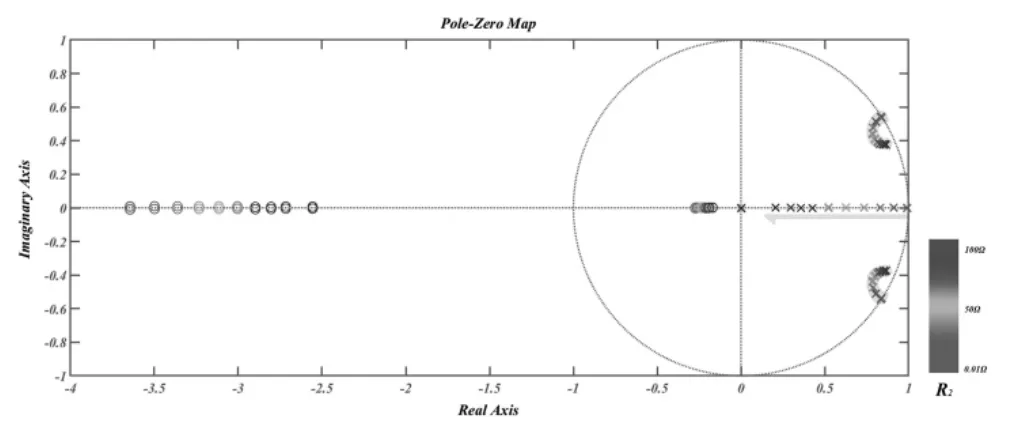
图1 带载变化时系统开环零极点图

1.2 控制器结构设计

在本文所提出的控制器结构中，外环由积分器构成，用于消除稳态误差与阶跃扰动，结构图如图2所示。矩阵Γ为静态解耦矩阵，用于校正状态反馈响应；整个控制器需要设计的参数只有K1与K2。

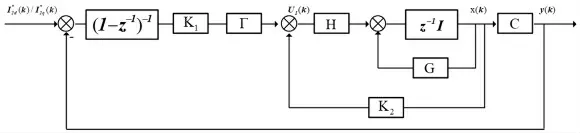
图2 伺服系统控制结构

将离散积分器的输出作为一个状态量，以K1作为反馈系数，得到PI控制器状态方程：

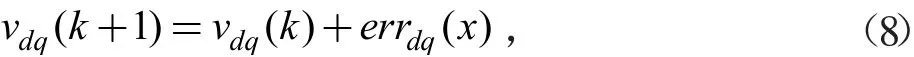
其中：

系统的控制率：

便可获得增广后的闭环系统：

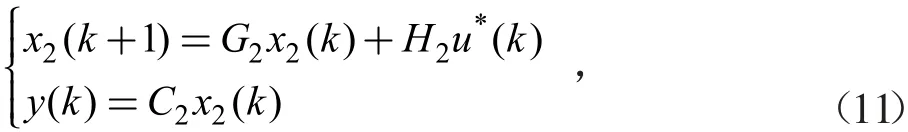
其中：

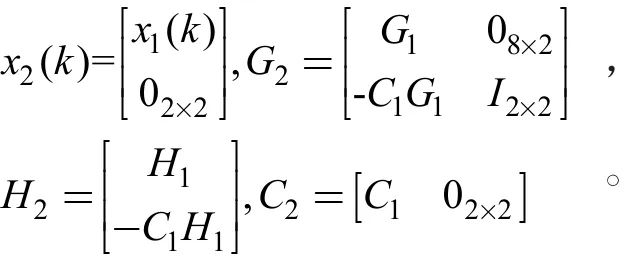
1.3 具有规定衰减速率的LQR控制器

经典控制理论设计控制系统，按照最优控制的观点，难免有根据经验试凑的嫌疑；而且控制器的结构在设计之初便以确立，形式上通常不是最优的。根据得到的离散线性系统，设计出二次型性能指标，使得控制系统实现控制任务时性能指标最小，这就是线性二次型最优控制。

而工程更加关心系统的品质指标，如主导极点分布、衰减速度、阻尼比等系统指标。

在一个二阶系统中，系统的极点由无阻尼振荡角频率。同时，这对极点也决定了系统的稳态响应与暂态响应。同样的，在一个高阶系统中，系统的动态性能也是主要由其闭环主导二阶极点对决定的。通过将除主导极点对以外的极点配置为远离主导极点的非主导极点，就可以使得高阶系统的响应性能接近由期望的主导极点决定的二阶系统。在设计高阶系统的时候，就是利用了这一基本原理来确定系统的控制参数，使系统具有期望的闭环主导极点对[8]，这样就可以近似地利用二阶系统的性能指标来设计系统。

以主导极点的衰减速度作为边界，建立如下二次型性能指标函数

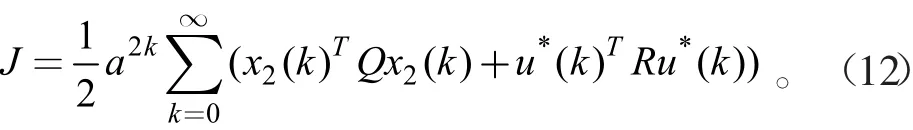
通过坐标变换x¯→akx，u→aku，可得坐标变换后的状态空间矩阵

与标准定常系统调节指标：

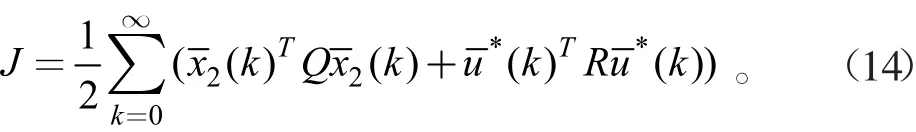
则对应的黎卡提方程为：

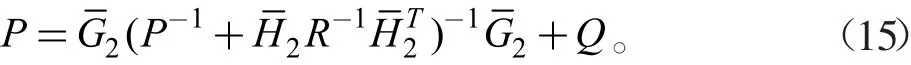
相应的最优反馈矩阵：

则最优控制序列为：

本文考虑结合两者的优点，提出具有规定衰减速度的离散系统的控制方案，同时能保证系统满足最优性。

2 仿真实验对比

2.1 仿真结果

按照计算的结果在simulink搭建模型并进行仿真，对比了传统双电流环PI结构与本文提出的控制策略的对比，可以得到图3和图4的数据对比。仿真所用数据如下，母线电压100 V，开关频率20 kHz，负载电阻1Ω，逆变器侧电感L1与负载侧电感L2为0.6 mH，滤波电容1 uF。在0.2 s时突变指令信号，由40 A降至20 A，在0.4 s时切除一半负载，由1Ω降至0.5Ω。

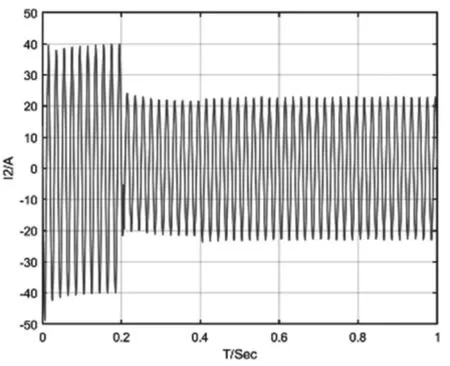
图3 双PI闭环输出电流波形

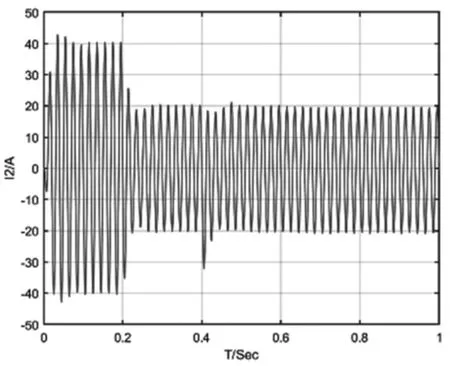
图4 PI+LQR输出电流波形

2.2 策略对比

由图3、图4可以看出，2种控制策略都基本能实现电流控制，两者的电流响应时间相近，大约为80 ms，但在响应过程中，双PI控制的超调量明显大于本文策略下的值，而且对控制指令跟踪的精度也有着较为明显的差距。