概率论在实变函数教学中的应用
2022-04-27郑前前杨文杰
郑前前,杨文杰
(许昌学院数理学院,河南 许昌 461000)
1 古典概型理论构建
本文通过概率论相关知识加深学生对测度相关知识的理解,进而利用测度解决一些概率问题。概率论发展初期主要的研究对象为古典概型,具有样本空间有限性及发生等可能性特点,下面我们讨论测度论在古典概型中的应用。
同理,随机事件B发生的概率为:


根据以上理论,同样可以得到

总结可得
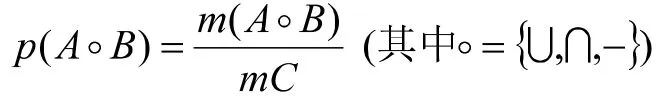
进而此方法也可以推广到有限交、有限并、条件概率等情况。
《中国储运》由《中国学术期刊 ( 光盘版 ) 》、《中国期刊网》(《知网》)、中国期刊全文数据库、CEPS中文电子期刊数据库、中国核心期刊(遴选)数据库全文收录。
此外,我们考虑更特殊的有限集、可数集及不可数集之间的概率问题,不妨设全集为实数集和为实数集R的子集且根据勒贝格测度可知这里假设的高阶无穷小,那么事件在实数集R的概率为


例如,一盒子里装有4 个小球,其中有3 个是白色小球,1 个黑色小球。从其中取球2 次,每次任取1 个。设事件A为“第1 次取到的是白球”,事件B为“第2 次取到的是黑球”。(1)作放回抽样情况下,求事件A,B的概率,事件A,B同时发生的概率。(2)作不放回抽样情况下求 。
解:(1)易知此题为古典概率问题,将球进行编号,1,2,3为白球。4 为黑球。


以上就是理论测度论解决古典概率的一般方法展示。
通过以上理论构造,我们发现在经典概率问题中,一些概率运算可以通过本文提出的理论进行简单运算,当然可能会使计算过程更为复杂,但本文的主要落脚点在于如何简化或者更容易使学生理解测度的定义及意义。古典概型问题的样本空间都是有限的,故其测度均为零。但零测度并不意味着集合为空,即概率为零时,事件并不一定不会发生或者存在。如此就可以把古典概型问题和其测度统一,两者相辅相成,从而克服实变函数教学中的困难。加深学生对所学知识的理解。同时我们规定

这也说明了在有限集、可数集、不可数集之间鸿沟的不可跨越性,即有限个有限集的并还是有限集,可数个可数集的并集还是可数集,不可数个不可数集的并还是不可数集。另外随机变量及其分布也可按照以上规则进行定义。
2 几何概型理论建立
几何概型的概率问题主要体现在测度的大小,同时测度往往不为零,其概率问题可以归结为简单函数的勒贝格积分,即一个随机事件可以表示为


下面考虑非负简单函数 勒贝格积分原理为

以上方法的引入也是几何概型理论的推广,黎曼积分无法积分的狄利克雷函数。在概率论中也是如此,所以几何概型的积分也可以进一步推广到勒贝格积分上。因为勒贝格积分都可以转化为简单函数的积分,以下我们就以简单函数为例说明勒贝格积分在概率中的应用。

令


通过以上例子可知勒贝格积分在几何概型分布函数理论中也可以得到广泛的应用,利用勒贝格积分函数和简单函数之间的关系,然后通过简单函数得到积分面积及其概率,总之在概率论中一些常见的概率问题都可以通过勒贝格积分进行解决,甚至更为简单、方便。
3 总结
实变函数作为数学分析的后续拓展课程,其理论同样适用于数学分析理论的应用领域。如概率论中几何概型的概率、期望及方差的计算。都可以使用勒贝格积分进行计算。以上理论的建立为实变函数论的教学方式形象化提供了理论依据。同时也是勒贝格积分广泛应用的一个经典案例,为学生进一步深度理解实变函数提供了可能。
