对水声定位滤波算法记忆衰减方式的改进

马建业 ，郑东健

(1.河海大学 水利水电学院，江苏 南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，江苏 南京 210098；3.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098)

水工建筑物的安全监测工作有助于把握工程的工作状态，评估其安全程度[1]。在智慧水利[2]的基本框架中，建筑物的安全监测工作处于基础的感知层[3]，由于水工建筑物工作环境的特殊性，有很大一部分长期位于水下，安全监测工作存在诸多困难。自动化的安全监测设备不仅有利于提高监测工作的安全性和便捷性，实时掌握水工建筑物的安全状态，而且有利于对运行管理提出指导性建议[4]。监测设备的水下定位具有基础性和关键性的作用，对水下定位算法的研究有利于提高水下建筑物安全监测工作的准确性和便捷性。

无线电磁波和光波等会在水下迅速衰减，无法在水下定位系统中使用。声波在水下可以远距离传播，是水下信息传播的主要载体[5]，水下定位大多为水下声学定位。在通信、导航、目标跟踪等过程中，不可避免地存在着由干扰因素引起的误差，例如水下声学定位中的水声环境噪声干扰误差、量测误差及系统误差等[6-7]。为在一定程度上抑制干扰噪声还原真实数据，数据滤波往往是目标定位系统中的重要组成部分。在众多的滤波算法中，最小二乘法（Least squares,LS）和卡尔曼滤波算法是应用较为广泛的两种经典算法[8]。其中，卡尔曼滤波因其能对现场采集数据的实时更新、便于计算机编程及其特有的数据融合功能等优势应用最为广泛，被认为是最佳的线性滤波器。在解决水声定位等非线性问题时，往往应用其非线性形式：扩展卡尔曼滤波（Extended Kalman Filtering,EKF）和无迹卡尔曼滤波[9]。传统卡尔曼滤波有一明显缺陷，即不准确的系统数学模型和噪声统计模型及由于计算机计算长度有限或是方法本身的近似处理而产生的误差会进行积累，从而使得误差矩阵失去正定性甚至对称性，导致滤波算法无法达到理论上的收敛。邱恺等[10]根据所提出的卡尔曼滤波过程的稳定性对滤波发散现象进行了较为清晰的定义。衰减记忆卡尔曼滤波[11]是解决此类问题的一个重要手段，衰减因子对滤波算法的性能影响较大，不适宜的衰减因子不仅对发散现象没有明显的抑制作用，而且还会加剧滤波算法的发散。关于衰减因子的取值，目前有两种常见的方法：一是传统的选取方法，即根据实际情况选取一个定值[12]，对环境的变化缺乏适应性，且受主观因素影响较大；二是采用自适应衰减因子[13]，使衰减因子在每一步的预测中都处于变化之中，这在一定程度上提高了衰减因子选取的灵活性。自适应衰减因子的确定主要有两种形式：函数型[14]和概率型[15-16]。自适应衰减因子虽提高了因子选取的灵活性，但仍需要主观确定全部或部分参数，且对滤波过程是否需要进行记忆衰减的判断未作出深入探讨。针对此问题，本文对水声定位算法中的扩展卡尔曼滤波进行了改进，其核心是在对滤波算法是否发散进行判定的基础上，以观测值为标准对记忆进行衰减。

1 算法描述

1.1 水声定位算法

传统水下目标定位几何算法可分为3 类[17]，本文选择较为简单的基于信号到达时间的（Time of Arrive,TOA）水声定位算法。如图1 所示，设观测节点A、B、C的坐标分别为（x1,y1）、（x2,y2）、（x3,y3）。定位目标T的坐标设为（x,y）。T与3 个观测节点之间的距离由所记录的信号到达时间计算：

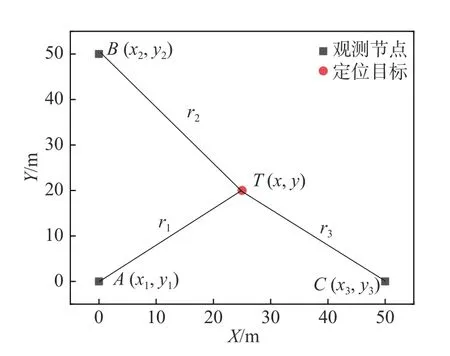
图1 目标定位算法示意Fig.1 Schematic diagram of positioning algorithm

式中：c为信号传播速度；ti为信号到达各观测节点的传输时间。

TOA 水声定位算法的基本原理如下所述，在定位目标T与观测节点A、B、C时间同步的条件下，移动目标节点T作为信号源发射测量信号的同时，发送一个同步信号给各观测节点，观测节点通过记录信号到达时间，计算定位目标与观测节点的距离。

根据几何关系，T的位置坐标可由式（2）计算：

式中：ri为目标节点与各观测节点之间的距离。

1.2 改进的衰减记忆卡尔曼滤波算法

在整个水声定位过程中，目标的真实位置是不可知的，无法以此为标准作出是否需要进行记忆衰减的判断。观测值理论上包含了真实位置的信息，可以用于判断滤波是否存在异常的发散现象。对衰减记忆卡尔曼滤波算法进行了改进，式（3）是本文对算法改进的数学表达。

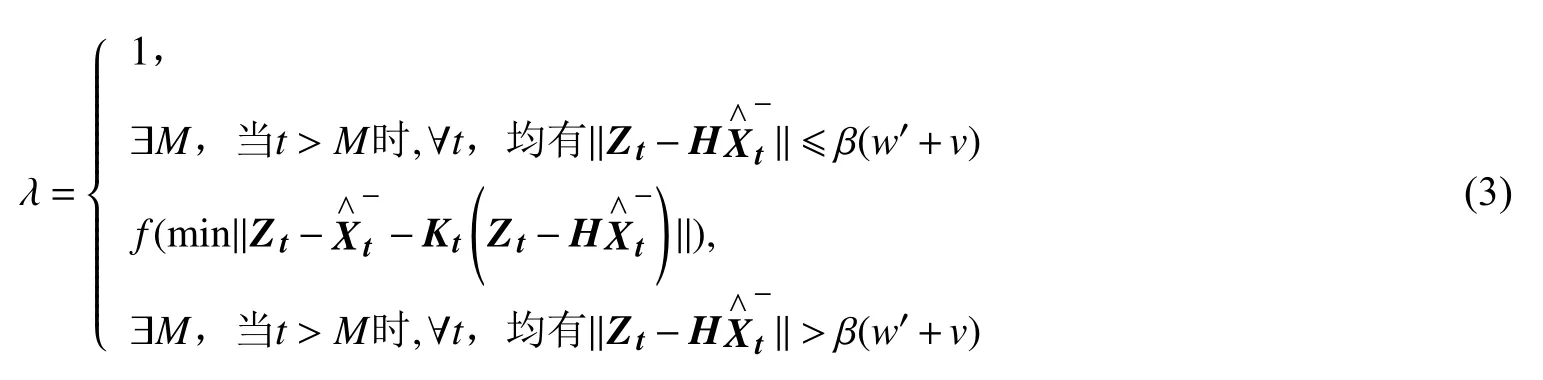
式中：λ为衰减因子；‖•‖为矩阵范数，在本式中其具体涵义为取矩阵各元素绝对值的最大值，可以较为容易地验证此定义下的矩阵范数满足正定性、齐次性和三角不等式；f表示以括号中的表达式为目标，对衰减因子进行寻优处理；H为转移矩阵，其作用是将状态域中的各元素转换到观测域参与计算；M为时间点；w’为预测模型的等效标准差，是根据观测方程式（2）和预测模型标准差w，并依据一般函数的误差传播定律求得的；v为观测模型的标准差；β为储备系数；式中其余字母含义与传统衰减记忆卡尔曼滤波算法中的定义一致。

如式（3）所示，本文对传统算法的改进主要包括：作出是否需要进行记忆衰减的判断；以观测值为标准，对记忆进行衰减。本文考虑到传统滤波发散判定方法的局限性[18]，采取以滤波过程稳定性[10]为基础的判断标准，该判断标准可以合理剔除正常的发散，如由于初始值设置不准确而导致的局部发散和观测野值等。

2 水下目标跟踪仿真试验

2.1 系统模型

本文以TOA 水声定位算法为例（图1），在平面区域进行仿真试验，3 个观测节点呈等间距的L 型布置，间隔为d=50 m。定位目标在运动过程中周期性地发出声信号，观测节点根据接收到的信号对定位目标的位置进行计算。

设3 个观测节点的坐标分别为A(0,0)、B(0,d)、C(d,0)，定位目标的坐标为T(x,y)。根据式（2）所述的定位原理，可得定位目标的坐标如式（4）：

式中：t1、t2、t3分别对应A、B、C接受目标信号的传播时间。

仿真试验的结果分析和比较标准采用式（5）所示的定位目标预测状态向量与实际状态向量之间的均方根误差表示。

2.2 参数选定

对滤波过程中参数的合理选定，不仅能够使仿真试验更加接近真实信号，增加仿真试验结果的可信度，还会对滤波效果产生明显影响，不合理的参数甚至会导致滤波发散。文献[19]讨论了影响扩展卡尔曼滤波的4 个因素，并给出了其选择原则。

被定位目标的初始状态X0对滤波效果有较大影响，合理的初始状态可以减小定位误差，加快滤波收敛，最好控制相对误差在12%以内。状态的初始噪声协方差矩阵P对滤波效果影响较小，可任意取一个非零矩阵，如单位对角矩阵。模型本身的噪声协方差矩阵Q取值越小越好。对于观测噪声的协方差矩阵R，工程上一般是在滤波前先测定噪声协方差，然后再用于后续的滤波。

根据文献[20]所述，短基线水声定位过程中，测量值的误差通常指传输时间误差，且具有随机性，脉冲前沿测量误差和时钟误差共同构成了时延误差，时钟误差可以通过精度较高的设备进行校对来避免，可忽略不计；而脉冲前沿的测量误差与信噪比相关，根据误差理论可知，由信噪比引起的时延误差符合统计规律，服从均值为0 的正态分布。

文献[7]提出了计算时延均方差的明确公式：

式中：W为可接收的信号带宽；Sn为信噪比（dB）。

根据1 kHz～1 MHz 标准水听器的行业标准[21]所述：“在实际测量条件下检测信噪比，其值应不小于30 dB”，而中心频率为200 kHz 的DYW-200-G 水声换能器的工作带宽为10 kHz。综合以上信息，本文选定时延均方差的数量级在10-4和10-6之间。

理论分析得出的模型本身的噪声和观测噪声均为高斯白噪声，这个条件在实际工程未必得到满足，并且各类环境误差和系统误差也是不可能完全被消除的。这些在滤波过程中未考虑到或是设定不准确的噪声误差可能会随滤波过程而逐渐积累，这也是需要引入衰减记忆滤波算法的一个重要原因。根据文献[7]对主流短基线水声定位系统的精度分析，其定位误差一般不超过3 m。故除常规噪声设置外，为仿真模拟系统数学模型不准确的情况，在状态转移过程中增加模型变化矩阵Bt。

式中：Xt为t时刻的真实状态；Ft为t时刻的状态转移矩阵。

2.3 仿真试验工况设置

仿真试验中涉及3 种不同的工况：（1）理想工况。初始状态X0、状态转移矩阵F、状态初始噪声P、模型本身噪声Q和观测噪声R等5 个参数均已准确设置。（2）实际工况。系统数学模型设置不够准确，存在一定的定位误差，且误差在主流水声定位系统的精度范围之内。（3）异常工况。初始状态X0设置不合理，与实际状态的相对误差超过12%，观测值存在一定的野值。

3 种工况下的模型本身噪声Q和观测噪声R，均分别设置为Q=diag(0.012m2)，R=diag(0.0022m2)，其中，diag 表示对角矩阵，其后括号里的数值为方差，矩阵维数分别与各自模型相适应。系统数学模型的不准确通过模型变化矩阵进行仿真。其他仿真参数设置如下：（1）理想工况。初始状态X0=S0（S0为定位目标实际初始状态），状态转移矩阵F准确，模型变化矩阵Bt为0。（2）实际工况。初始状态X0中各元素与S0（S0为定位目标实际初始状态）中各元素的相对误差均小于12%，状态转移矩阵F不准确，模型变化矩阵Bt非0，且标准差不超过3 m。（3）异常工况。初始状态X0中各元素与S0中各元素的相对误差均大于12%，状态转移矩阵F准确。观测值在预测过程中的个别时间点存在野值。

3 仿真试验结果与讨论

3.1 衰减记忆方法的合理性验证

实际情况下，由于目标真实状态无法获取，故无法根据目标状态真实值与最终预测值之间的均方根误差 δ1判别系统是否存在发散趋势。故本文认为状态的初步预测值与观测值所反映的状态之间的均方根残差δ2一定程度上可以反映目标状态真实值与最终预测值之间的 δ1变化趋势，可据此来选择是否需要进行记忆衰减。

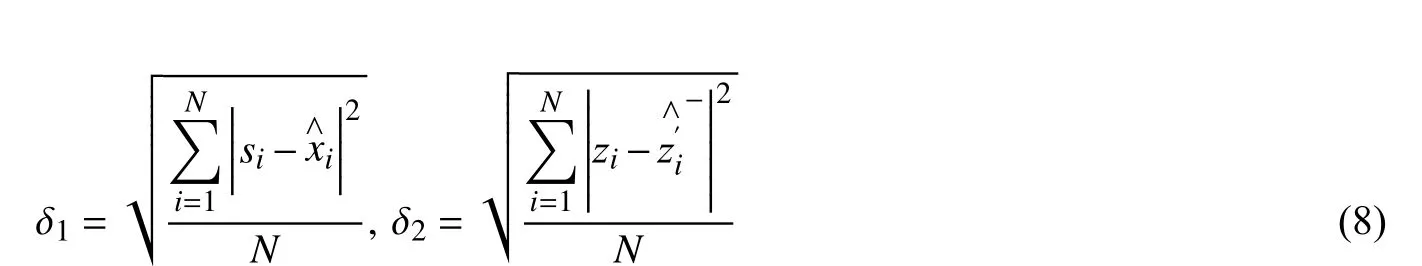
式中：si为目标各状态分量的真实值；为目标状态最终预测值；zi为观测值；为目标状态初步预测值在观测域的各等效分量，由观测方程计算得到。

根据实际工况，选取预测模型噪声协方差矩阵Q=diag(0.012m2)，观测模型标准差R=diag(0.022m2)，预测模型变化矩阵为均值为0 m、标准差为2.5 m 的随机矩阵，在此条件下进行水下目标定位仿真试验，记录δ1和δ2，两者趋势关系在图2 中得以体现。

从图2 中可以看出，两类均方根误差的变化趋势基本相同，且 δ2对 δ1有一定程度上的放大效果。试验结果表明，可根据目标状态的初步预测值与观测值之间的离散程度来判断系统是否有发散趋势，并以此作为是否需要进行记忆衰减的判断依据。作为是否需要进行记忆衰减的判断依据，δ2的大小可能与衰减因子具体数值的选取具有一定的相关性。并且衰减因子的引入主要是为了解决由误差累积所引起的系统发散问题，从这个角度分析，衰减因子还可能与预测时长具有一定的相关性，已有研究成果也利用了此种关系[14]。

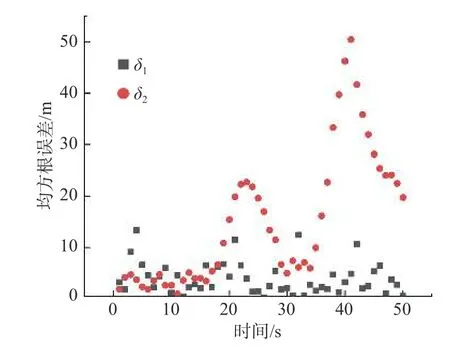
图2 均方根误差变化趋势对比Fig.2 Comparison of RMSE change trends

为此，本文在预测模型噪声协方差矩阵为Q=diag(0.012m2)，观测模型协方差矩阵为R=diag(0.022m2)，预测模型变化矩阵的均值为0 m、方差为0.05 m2的随机矩阵的条件下，进行水声定位仿真实验，记录目标状态初步预测值与观测值之间的残差，并经过归一化处理后，求得 δ2。根据目标状态真实值与最终预测值之间的均方根误差最小的原则，进行衰减因子的寻优，并对试验结果进行了相关分析。

计算结果表明，最优衰减因子与两个变量之间的双尾显著性分别为-0.053 和0.186，其绝对值均大于0.05，这表明显著性不高；且相关系数分别为0.275 和-0.190（表1），其绝对值均小于0.3，这表明无相关性。故本试验中，难以用确切的函数表达式将 δ2和预测时长两个变量与衰减因子联系起来。

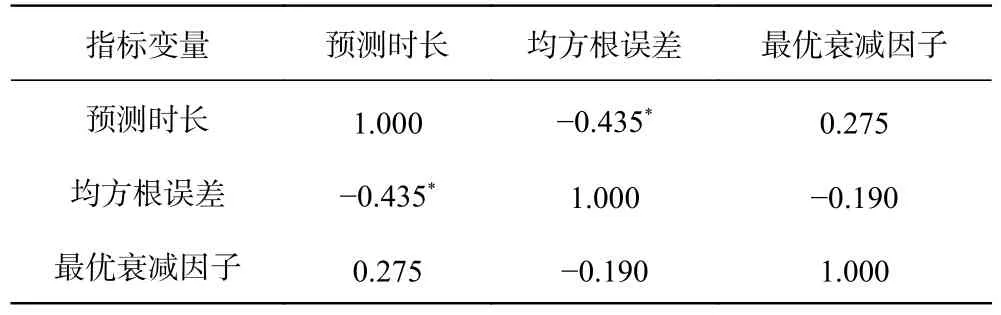
表1 衰减因子相关分析Tab.1 Correlation analysis of attenuation factors

综合分析以上两部分的试验结果，本文提出如式（3）所示的衰减因子选取的改进算法，其主要步骤是根据目标状态的初步预测值与观测值之间的离散程度，对滤波算法作出是否有发散趋势的判定后，以观测值为标准对记忆进行衰减。

3.2 对比试验

为验证改进的算法（Improved fading memory Kalman filter algorithm,IFMKF）性能，本文在3 种工况条件下，在水声定位仿真试验中，对其与传统衰减记忆滤波卡尔曼滤波算法（Traditional fading memory Kalman filter algorithm,TFMKF）和指数型加权自适应衰减记忆卡尔曼滤波算法（Exponential weighted adaptive fading memory Kalman filter algorithm,EWFMKF）的定位精度进行比较。TFMKF 算法中的衰减因子，根据文献[12]的研究结果，选定为1.23。EWFMKF 中参数b，按照文献[14]所述，取0 到1 之间的数值。分别记录水下目标跟踪过程中定位过程的坐标位置均方根误差。

图3 是理想工况下的3 种算法的均方根误差比较。在水声定位中，当各类参数均准确或接近准确设置时，水声定位工况接近理想工况，滤波过程稳定，没有发散现象，无需进行记忆衰减。从图3 可见：3 种定位算法在30 s 之前的均方根误差大小及变化趋势基本相同，但在之后的定位过程中，由于TFMKF 和EWFMKF 两种滤波算法进行了记忆衰减，反而对定位精度产生了负面影响。从表2 中可见IFMKF 的累计定位均方根误差均小于TFMKF 和EWFMKF，定位精度分别相对提高19.4%和21.4%。

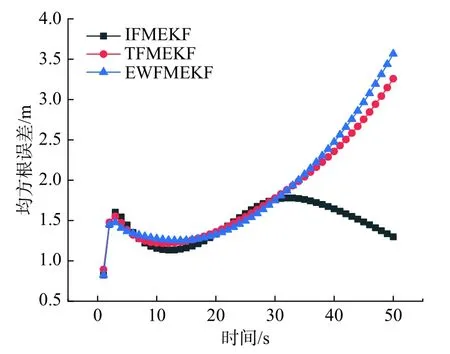
图3 理想工况下3 种算法的均方根误差比较Fig.3 RMSE comparison of the three algorithms under ideal conditions

图4 是实际工况下的3 种算法的均方根误差比较。在水声定位中，当各类参数均欠准确或不准确设置时，水声定位工况接近实际工况，滤波过程不稳定；随着滤波过程的推进，误差会进行累积，造成定位精度的发散，属于异常发散，需要进行记忆衰减。本文在此种工况下，设定系统状态转移模型设置不够准确，模型变化矩阵Bt的元素为1～2 m 间均匀分布的随机数。初始状态设置也与实际状态存在6%的相对误差。从图4 可以看出，3 种算法在水声定位过程中的均方根误差变化趋势基本相同，大小存在差异。从表2 可见，IFMKF 的累计定位均方根误差均小于TFMKF 和EWFMKF，定位精度分别相对提高78.4%和48.8%。由于仿真试验中设定系统状态转移的数学模型不准确，而观测模型准确设置，故可能会导致定位精度提高百分比较大，但精度提高的整体趋势不变。

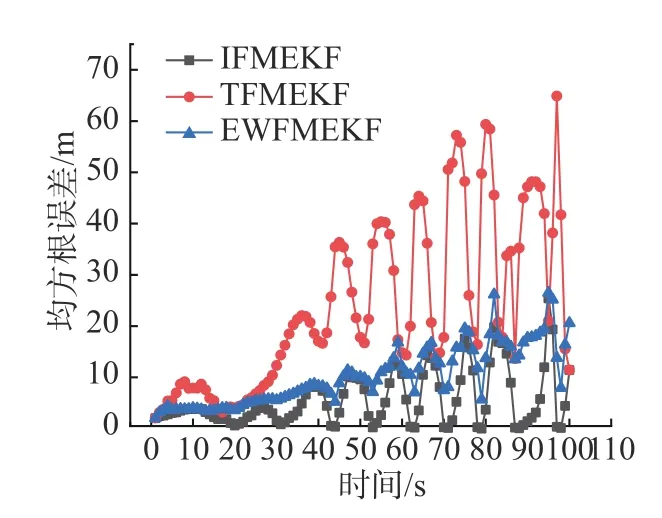
图4 实际工况下3 种算法的均方根误差比较Fig.4 Comparison of RMSE of the three algorithms under actual working conditions

表2 不同记忆衰减方法的累积定位均方根误差Tab.2 Cumulative root mean square error of different memory attenuation methods

图5 和6 是异常工况下3 种算法的均方根误差比较。在水声定位中，除初始状态外，当各类参数准确或近似准确设置，且观测值存在个别野值时，水声定位工况接近异常工况；虽然在个别时间内，定位结果与实际位置存在较大误差，但滤波过程稳定；随着滤波过程的推进，误差不会进行累积，不需要进行记忆衰减。本文在此种工况下，设定系统初始状态与实际状态存在20%的相对误差，在15 s 时刻，观测值出现一个异常的野值。

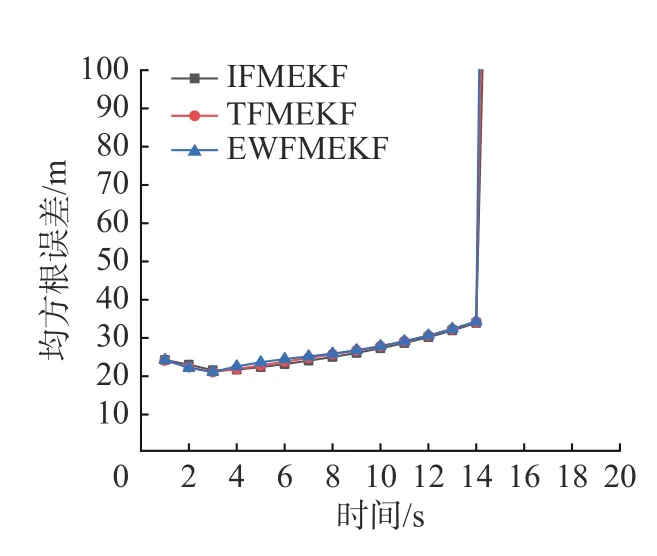
图5 异常工况下3 种算法观测野值出现前的均方根误差比较Fig.5 Comparison of the RMSE of the three algorithms before the occurrence of outliers under abnormal conditions

从图5 可以看出：在野值出现前，由于初始状态的不准确设定，定位误差在初始的6 s 内出现了小幅度的增大，但又很快得到了抑制，属于正常的发散现象，不需要进行记忆衰减；而3 种算法在这段时间内的定位精度及变化趋势基本相同。

从图6 可以看出：在野值出现之后，TFMKF 和EWFMKF 两种滤波算法与IFMKF 相比使得定位误差陡然升高，对水声定位精度产生了负面影响。需要剔除野值，不应以此判断滤波发散。相较于其他两种方法，由于IFMKF 以整个滤波过程为判断依据，故在有观测野值的工况下，定位误差没有急剧上升，定位效果更优。由于观测野值出现后，定位误差的陡然升高，故定位精度不具有可比性，因此异常工况试验条件下的试验结果在表2 中不再进行精度比较。

图6 异常工况下3 种算法的均方根误差比较Fig.6 RMSE comparison of the three algorithms under abnormal conditions

4 结语

本文对水声定位中的扩展卡尔曼滤波算法进行了改进，为水声定位中的扩展卡尔曼滤波算法的记忆衰减方式提供了一种新的思路和方法。改进算法以定位过程中观测值与初步预测值之间的差值为判断依据，以滤波过程的稳定性为判断原则，作出是否需要进行记忆衰减的判断后，以观测值为标准进行记忆衰减。将改进的算法应用于3 种不同工况的水声定位仿真试验中。仿真结果表明，较TFMKF 和EWFMKF 两种算法，改进算法的记忆衰减方式更为准确和灵活，能有效避免对算法是否需要进行记忆衰减的误判，定位效果和定位精度得到了提高。