基于EDMD与改进KPCA算法的机械设备故障诊断方法*

金樟民 方学宠 娄益凡 张富齐

1温州市特种设备检测院 温州 325000 2武汉科技大学 武汉 430081

0 引言

随着现代化进程的加快，以起重机、发电机等为代表的旋转机械作为工业设备的关键组成部分，正朝着集成化、智能化等方向发展，并在绿色制造、冶金加工、交通运输等领域发挥着重要作用[1]。由于复杂的系统结构以及恶劣的运行条件，其内部的关键零部件在工作中出现故障的概率越来越高。机械设备故障诊断技术作为保证设备安全可靠运行的重要措施，不仅可以准确地对各种异常状态做出判断，还可以预测故障原因并对此提出相关对策及建议[2]。因此，及时有效地对机械设备运行状态进行监测和诊断，对于提高其使用效率，避免重大安全事故发生等方面具有重大意义[3]。

通常，利用振动信号分析方法对机械设备故障信号进行处理是最常用也是最有效的手段。在此方法中，识别和提取信号特征是整个故障诊断的关键[4]。经验模式分解（以下简称EMD）是一种自适应分解信号的算法，用于分析来自非线性系统的非平稳信号[5]。虽然EMD在工程领域已被广泛应用，但是其在对信号进行分解时易出现模式分量混叠和端点效应等问题[6]。集成经验模式分解（以下简称EEMD）是Wu Z H等[7]提出的一种利用高斯白噪声辅助的模式分解算法。该算法通过随机在待分析信号中添加不同幅值的白噪声，并计算均值得到相对应的模态分量，从而改善模式混叠的现象。由于EEMD在去噪时可能会导致部分分量上的有效信息被淹没，故其也存在信号失真的情况[8]。动模式分解（以下简称DMD）是一种基于数据驱动的模态分解算法，在其固有的空间结构中可以将复杂流场分解为一系列简单的表达[9]。DMD虽然结合了时空降维和本征正交分解的优点，但对复杂含噪信号的分解能力却有一定的欠缺[10]。扩展的动模式分解（以下简称EDMD）[11]作为DMD的扩展算法，是一种逼近Koopman算子谱特性的数值方法，观测函数的选择是EDMD应用于非线性问题的基础。本文从动力系统模型出发，通过李导数将观测函数提升，使观测函数成为多项式形式。这种多项式形式的变换是精确的，并且它提供了一组足够的可观测函数。与传统的DMD方法相比，EDMD更适用于更广泛的非线性动力系统，除此之外，EDMD保留了底层动力系统的物理可解释性，并且可以很容易地集成到现有的数值库中。基于上述分析，为了更准确地提取强噪声背景下微弱的故障信号特征，本文采用EDMD对机械设备的振动信号进行分解，获得能够表征机械设备实时状态的特征分量，进而进行后续分析。

核主成分分析法（以下简称KPCA）是一种常用的数据分析方法[12]。作为主成分分析法（以下简称PCA）的改进算法，其利用核函数的特点，克服了PCA在处理非线性数据时信号特征信息容易丢失的问题，具有很好地非线性特征提取能力。KPCA算法虽然保留了样本的全部特征信息，但却未保留样本的类别信息，导致其最后未能达到最好的分类效果。为此，针对KPCA在分类问题上的缺陷，引入改进的KPCA算法。该算法在KPCA所得结果的基础上，通过提取的特征向量的类内聚集程度和类间离散程度来描述样本的类别信息，在保留了较好降维效果的同时，更好地实现了后续样本特征的聚类分类。

综合以上分析，本文在动模式分解和核主成分分析的基础上，提出基于EDMD与改进的KPCA算法的机械设备故障诊断方法。首先利用EDMD对振动信号进行分解，得到一系列多元模式分量，并删除会对特征提取产生干扰的无关分量和计算多个统计学特征，然后通过改进的KPCA算法对这些保留下来的样本数据进行降维和聚类，从而达到监测和诊断机械设备故障的目的。

1 理论描述

1.1 扩展的动模式分解算法（EDMD）

1.2 改进的核主成分分析算法（improved KPCA）

由上式可知，特征值ξi压缩了原始信号中所包含的信息，故可通过特征值和特征向量来对故障模式进行分类。

设一个非线性映射函数φ（x），并将原始特征集W=[w1,w2,…,ws]T转化为核特征集 W′ =[φ(w1),φ(w2),…,φ(ws)]T。其中s为样本数量。则核特征集的协方差矩阵F表达式为

式中：ε为第i类样本的数量，βaij为第i类里第j个样本的第a维分量。根据式（18）和式（19），可得样本类别可分离程度为

当Ja的值越小时，说明样本类别的可分离程度越高，对样本分类的贡献程度越大。为了说明提取的特征向量与样本类别向量之间的相关程度，定义其表达式为

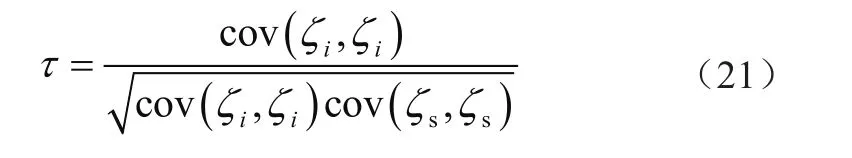
式中：τ为相关程度系数，ζi为提取的特征向量，ζs为原特征集中的样本类别向量。

若τ绝对值趋近于1，则表示2向量相关性越强；若τ绝对值趋近于0，则表示其相关性越弱。因此，根据τ的值，保留对样本分类贡献程度高的特征向量，减少无效样本的干扰，提高后续对故障分类的精度。

本文所述方法的整体流程如图1所示。技术路线主要包括4个步骤：1）通过加速度传感器采集齿轮箱的振动信号；2）对采集到的振动信号进行EDMD分解，获得能够表征齿轮箱实时状态的有效IMF分量；3）对有效IMF分量进行时域、频域上的特征提取，主要提取平均值、最大值、最小值、有效值、方根幅值、峭度、歪度、频率重心、频率方差、频率均方、频率均方根、频率标准差12个统计学分量，形成高维特征矩阵；4）采用KPCA对上述高维特征矩阵进行数据降维，实现对齿轮箱不同故障模式的聚类识别。

图1 整体流程

2 数值仿真分析

在不失一般性的前提下，首先进行仿真分析，验证本文所提方法在信号分解方面的稳定性。本节设置的仿真信号模型为

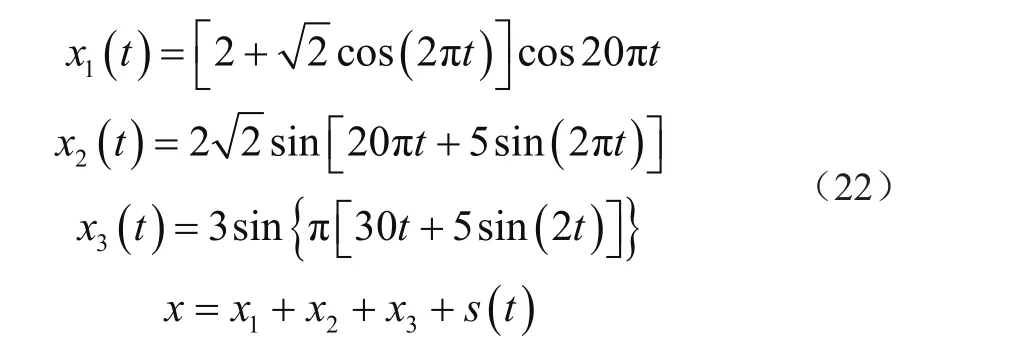
为了模拟真实的液压泵故障信号，将3个仿真信号组成一个具有调幅-调频性质的随机混合信号。同时考虑到噪声分量，加入SNR=10 dB的高斯白噪声来模拟实际情况。则该混合信号的时域图和各模式分量图如图2所示。

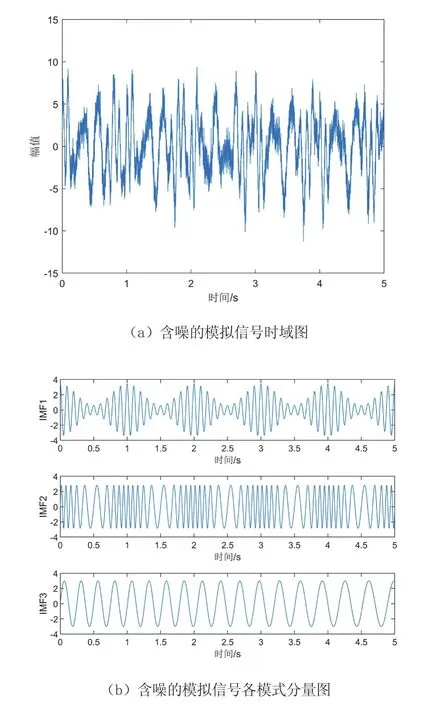
图2 含噪的模拟信号时域及模式分量图

分别利用EMD、EEMD以及MEMD对该仿真信号进行处理，各方法提供的分解结果如图3所示。

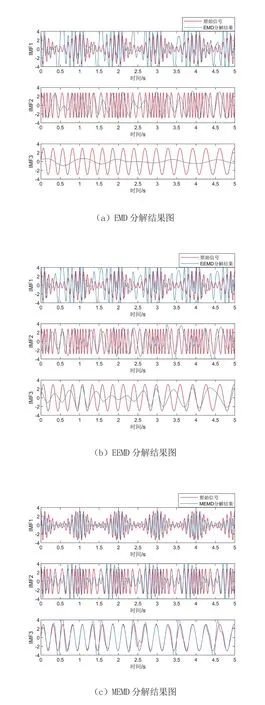
图3 EMD、EEMD和MEMD分解结果与原始信号对比

从图3可知，EMD与EEMD受噪声分量的干扰较大，各信号分量不能很好地被识别出来。MEMD提高了对多分量信号特征提取的能力，在保证分解稳定性方面具有一定的优势。其提供的IMF2和IMF3的形态特征仍与原始输入信号有较大差别。为此，利用EDMD算法对数值仿真信号进行处理，分解后的对比结果如图4所示。由图4可知，EDMD将模拟混合信号中的各模式分量完整地分解出来，所提取的脊线特征与原始信号相比有着更高的相似度，很好地解决了其他分解算法在处理复杂含噪信号时存在的解析能力较差的问题。

图4 EDMD分解结果与原始信号对比图

通常，均方根误差（以下简称RMSE）反映了信号分解结果与真实值之间的误差程度，误差值越小，表明信号分解的精度越高，故可将RMSE作为评定这一分解过程精度的标准。上述各分解算法所得结果与原始信号真实值之间的RMSE值如表1所示。通过表1中数据可知，EDMD分解后的结果与原始信号的偏离程度最小，可以将其作为识别和提取机械设备故障特征频率的可靠性工具。

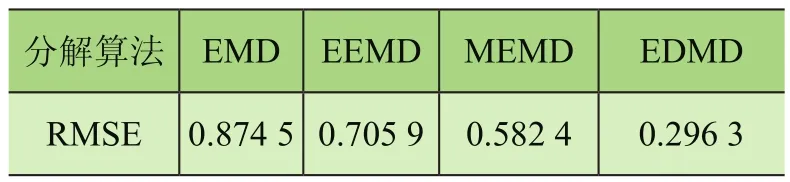
表1 各算法分解结果的RMSE值

3 实验研究

为了验证本文所提方法的有效性，采用齿轮箱故障模拟综合试验台的实验数据进行分析。平台装置选择单极齿轮传动，以2 000 Hz的采样频率采集齿轮振动信号，电动机型号为YDF801-4，高速轴的转速为363 r/min。实验装置及其结构图如图5所示，其中采集信号的振动加速度传感器安装在图中2处的轴承座上。相关试验装置参数如表2所示。测试时，分别采集多组齿轮正常、周节误差和磨损等3种状态下的样本数据，然后对这些数据进行模式分解，并剔除噪声分量，最后通过降维和聚类分析区分出不同的齿轮故障特征。

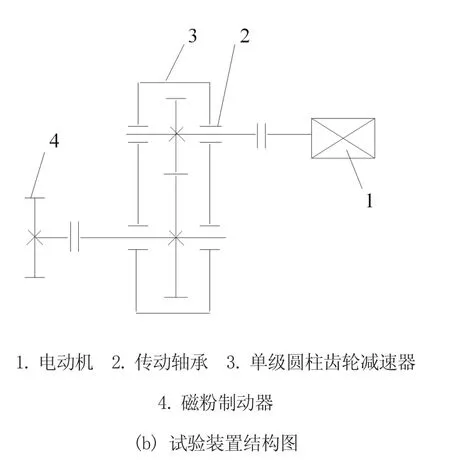
图5 实验装置及其结构图

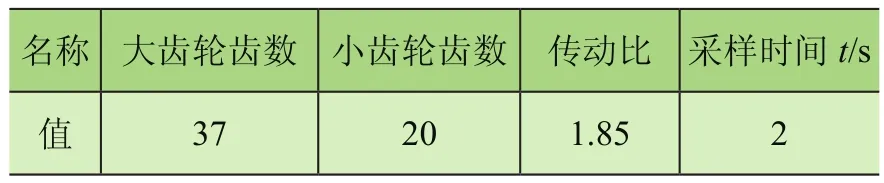
表2 试验平台装置相关参数

图6中分别给出了其中1组齿轮正常状态、周节误差和磨损故障信号的时域图和频域图。

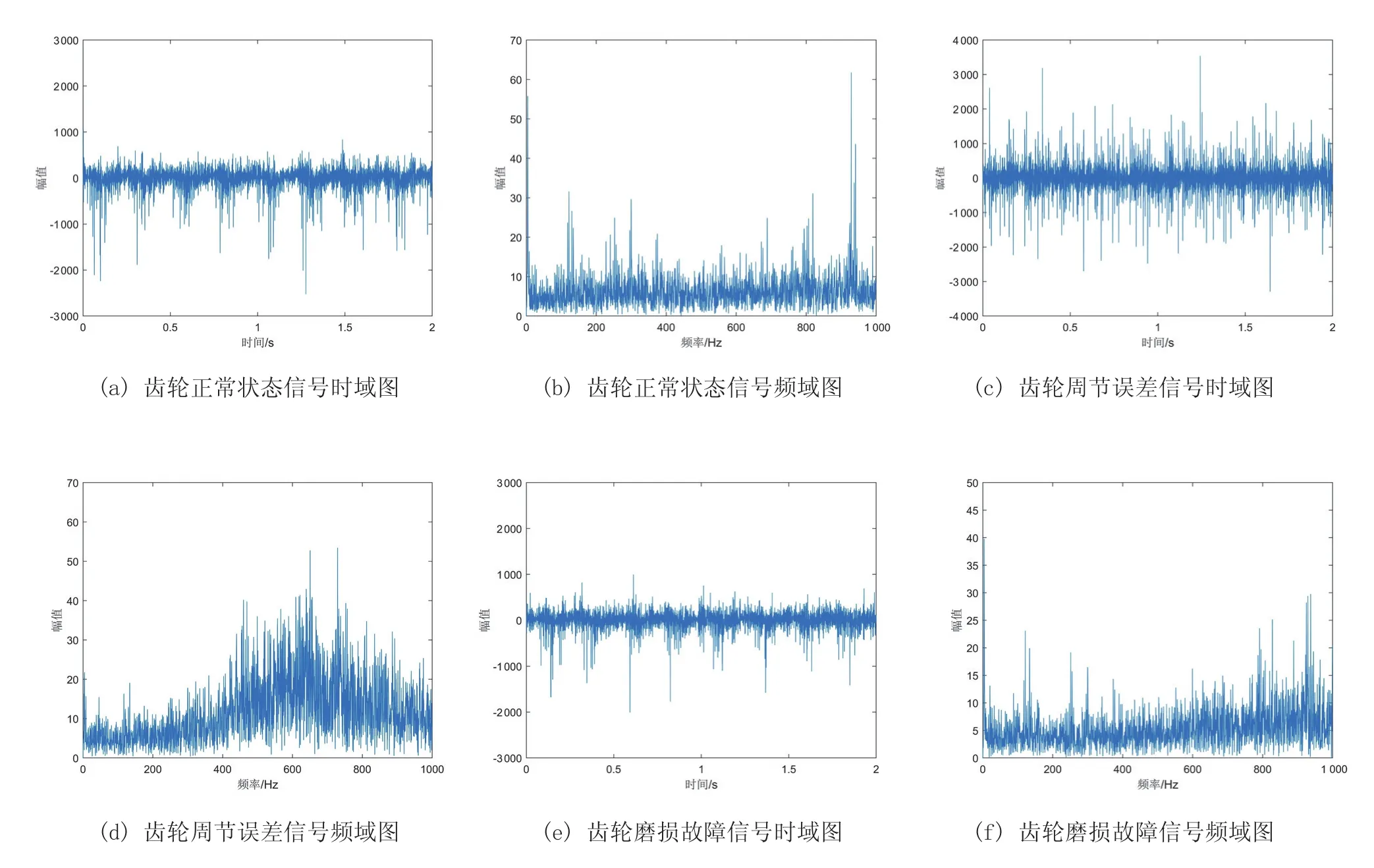
图6 齿轮不同状态信号时域和频域图

通过上述频谱分析可知，齿轮不同状态信号的频域特征不明显。因此，使用扩展的动模式分解（EDMD）对以上3种振动信号进行分解。所得分解结果如图7所示。

图7 齿轮不同状态信号分解图

对经EDMD分解后的不同模式分量进行相似度分析，去除冗余信号的IMF分量，获得能够反映齿轮箱实时状态的有效IMF分量；接着计算有效IMF分量的时频域12个特征参数，从而形成高维特征矩阵，然后利用改进的KPCA算法对得到的高维空间数据进行降维预处理和特征聚类分析，处理后所得三维聚类图如图8所示。

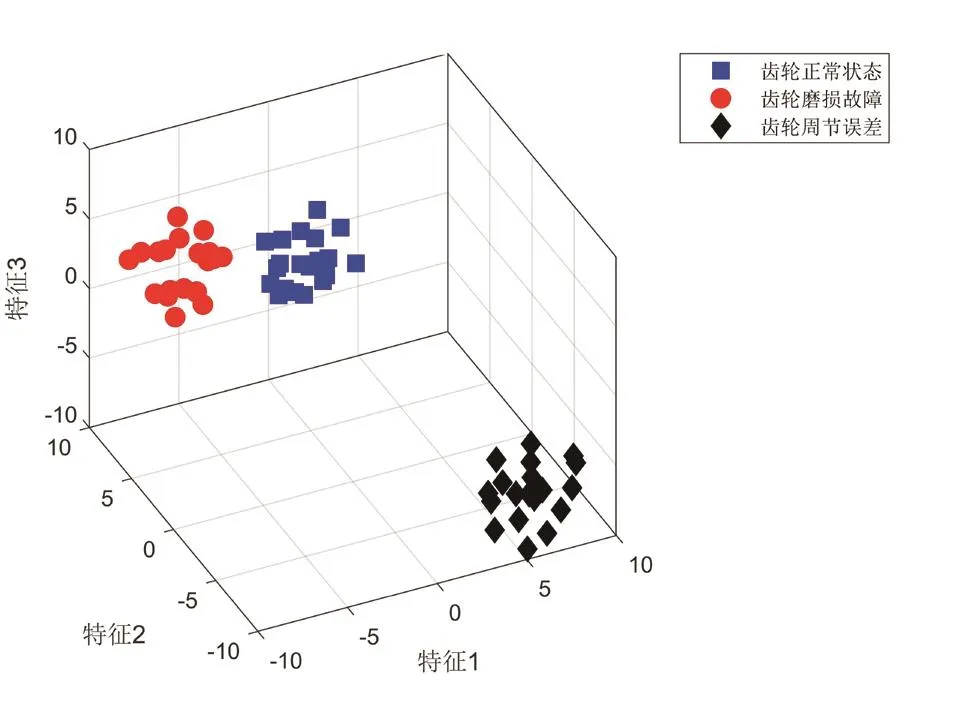
图8 改进的KPCA算法对齿轮故障的聚类结果

为了进一步验证本文所提出方法在机械设备故障特征辨识方面的优越性，直接运用传统的LPP和LLE算法对原始数据计算统计学特征并进行降维和样本聚类。各算法所得结果如图9所示。同时根据以上聚类结果，分别计算了各算法在聚类数据上的正确率，其结果如表3所示。

表3 3种降维算法的聚类正确率 %

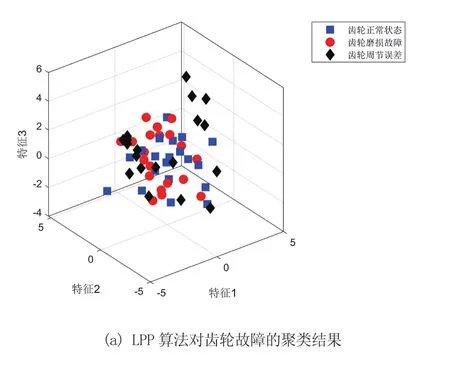
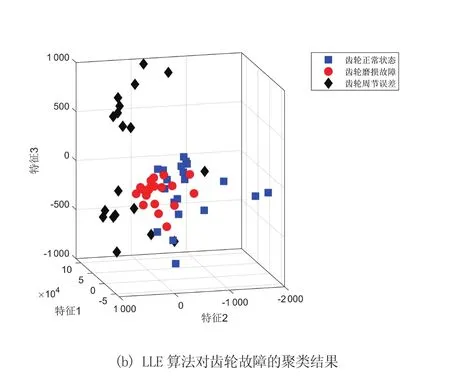
图9 其他降维方法对齿轮故障的聚类结果

通过图8、图9以及表3中的数据可以看出，相比于其他2类算法，本文提出的改进EDMD和改进KPCA算法具有最高的聚类正确率，其在降维预处理和特征分类方面的能力有了显著提升，可以成为一种有效地设备在线监测和数据分析的手段。

4 结论

1）通过EDMD对采集到的机械设备振动信号进行分解，解决分解过程中因分量时频特性差异所带来的模式混淆的问题，提高了分解结果的准确性。

2）利用改进的KPCA算法，对分解后有用分量的高维数据特征进行降维处理，在最大程度保留信号特征信息的情况下，让数据结构变得更加精简，然后依靠其在非线性问题处理上的优势对低维样本进行聚类，从而显著提高对机械设备故障判别的正确率。

3）将所提出方法运用到试验台所采集的齿轮故障信号分析中，试验证明该方法满足了对机械设备状态监测和故障诊断的适用性要求。