基于分子动力学模拟的石墨烯镁基复合材料力学行为*

明知非 宋海洋 安敏荣

(西安石油大学材料科学与工程学院,西安 710065)

镁合金因其低密度被视为最轻的工程结构金属材料,但因较差的塑性变形行为限制了其广泛应用,因此增强镁合金的综合力学性能已经成为当前材料领域的研究热点.本文采用分子动力学模拟方法,研究了在拉伸载荷下石墨烯对金属镁变形行为和力学性能的影响.研究结果表明,石墨烯的嵌入能够明显提升金属镁的强度和杨氏模量,并对其塑性变形阶段的第二次应变强化产生较大影响.研究指出,石墨烯镁基(GR/Mg)复合材料和纯镁的塑性变形行为相同,在塑性变形过程中均发生了从密排六方到体心立方再到密排六方结构的相变.石墨烯嵌入位置对GR/Mg 复合材料上下两部分镁基体的塑性变形行为有较大的影响.当石墨烯嵌入高度较小时,石墨烯下方的镁基体塑性变形能力较强,容易发生位错滑移,而当石墨烯嵌入高度较大时,石墨烯上下方的两部分镁基体的塑性变形能力相当,它们的塑性变形行为趋于同步.此外,本文对镁基体的相变机制也进行了详细分析.本文的研究结果对于设计高性能的石墨烯金属基复合材料具有一定的理论指导意义.

1 引言

镁及镁合金作为最轻的工程结构金属材料,具有许多优异的性能,在航空航天、汽车和医疗等领域具有广阔的应用前景,被誉为21 世纪的绿色结构材料[1].然而,镁及镁合金存在塑性差、高温强度低等缺点,这严重限制了镁及镁合金的广泛应用.因此,如何有效地提高镁及镁合金的塑性变形能力,增强镁及镁合金的综合性能,是拓宽镁及镁合金应用前景的关键问题.近年来,越来越多的研究人员都致力于探寻新型结构的镁及镁合金,并提出一些增强镁及镁合金力学性能的有效方法[2,3].Song和Li[4]首次从理论上提出了晶体/非晶双相镁合金纳米结构模型,该策略可以有效地改善金属镁的塑性变形能力,通过合理设计非晶相和晶体相的匹配关系可以获得综合力学性能优异镁合金.Wu 等[5]采用磁控溅射技术首次成功制备出了非晶/晶体镁基超纳双相薄膜材料,研究指出该材料具有超高的强度(3.3 GPa)和良好的塑性.Ding 等[6]研究了稀土镁合金的变形行为,研究发现,稀土元素的加入可以有效激发镁中锥面 〈c+a〉 位错滑移系产生更多位错滑移,从而提高镁合金的综合性能.虽然目前人们在提高镁合金力学性能的研究中取得了一系列研究成果,但与人们预期的要求仍然有着较大差距,镁合金在工业上的应用仍有很大的局限性.

石墨烯由于其优异的力学性能,被认为是最理想的金属基复合材料的增强体,受到了国内外学者的广泛关注,并取得了丰硕的研究成果[7−13].Kim等[14]以单层石墨烯为成分合成了高性能的石墨烯铜基复合材料和石墨烯镍基复合材料.Rezaei[15]研究了石墨烯金属纳米层复合材料的力学行为,研究发现,石墨烯的加入显著提高了复合材料的强度和韧性.Wang 等[16]通过分子动力学模拟方法,研究了铝基体中单层石墨烯在单轴拉伸下的力学性能.结果表明,石墨烯层能有效地阻断界面间位错的扩展,从而显著提高复合材料的刚度和强度.目前,人们对石墨烯增强金属基复合材料力学性能的研究主要集中在面心立方(face centered cubic,FCC)结构的金属材料,而对于具有密排六方结构(hexagonal close packed,HCP)的镁及镁合金的研究仍然不足.Zhou 和Liu 等[17]采用分子动力学模拟方法对石墨烯镁基(GR/Mg)复合材料在单轴拉伸作用下的力学性能进行了研究,指出石墨烯的嵌入可以显著增强金属镁的力学性能.Xiang 等[18]采用多步分散法制备了GR/Mg 复合材料,发现石墨烯的嵌入使得复合材料的极限抗拉强度、杨氏模量和延伸率都明显提高.当前,虽然对GR/Mg 复合材料力学性能的研究已经取得了初步成果,但GR/Mg 复合材料的微观变形机制和强化机理仍不清楚,有待进一步揭示.本文采用分子动力学模拟方法研究了石墨烯对金属镁在拉伸载荷下的变形行为和力学性能的影响,阐明了石墨烯嵌入位置对GR/Mg 复合材料力学性能的影响规律.本文的研究结果为进一步设计高性能的石墨烯镁金属基复合材料提供了一定的理论依据.

2 模拟方法和模拟过程

运用LAMMPS[19]软件,采用分子动力学模拟方法研究了在单轴拉伸载荷下石墨烯嵌入位置对GR/Mg 复合材料变形行为和力学性能的影响.Du等[20]在实验中制备GR/Mg 复合材料时发现,石墨烯会呈现择优沉积,沉积于镁合金基面上.因此,构建了金属镁基面(即YZ平面)与石墨烯平行的GR/Mg复合材料模型进行研究,模型尺寸为14.4 nm ×21.4 nm × 37.4 nm 的GR/Mg 复合材料模型,如图1(a)所示.嵌入的石墨烯在Y和Z两个方向的尺寸分别为15.3 nm 和37.4 nm,石墨烯结构如图1(b)所示.为了阐明石墨烯嵌入位置对GR/Mg 复合材料力学行为的影响,构建了5 个石墨烯嵌入高度(h)分别为0.1L,0.2L,0.3L,0.4L,0.5L的模型,其中L为GR/Mg 复合材料在X方向上的尺寸.为了方便起见,用GRx/Mg (x=0.1,0.2,0.3,0.4,0.5)描述不同嵌入高度的复合材料模型.GR/Mg复合材料模型含有大约531000 个原子.镁基体在X,Y,Z方向晶向分别为[0001],,石墨烯在Z方向上为锯齿型取向.在模拟中,所有模型的Y和Z方向均采用周期边界条件,而X方向采用自由边界条件,并通过Nose-Hoover 方法进行温度控制.在模拟中,沿模型的Z方向施加拉伸载荷,应变率为109s–1.

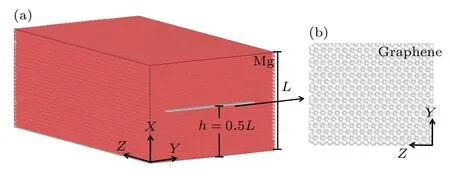
图1 (a) GR/Mg 复合材料的初始模型;(b) 嵌入石墨烯的原子快照图,其中红色原子为镁原子,灰白色原子为碳原子Fig.1.(a) The initial model of GR/Mg composites;(b) the atomic snapshots of embedded graphene.The red atom is magnesium atom,and the gray and white atom is carbon atom.

在分子动力学模拟中,势函数的选择是获得合理结果的关键因素.用组合势来描述原子间的相互作用,镁原子之间的相互作用采用Sun 等[21]开发的经验嵌入原子方法势来描述,碳原子之间的相互作用采用自适应分子间反应键序势[22]进行描述,镁原子和碳原子之间的相互作用采用Lennard-Jones 势[23]来描述.在施加拉伸载荷之前,所有的模型首先采用共轭梯度能量最小化算法达到一个平衡结构.采用可视化工具(OVITO)[24]分析施加拉伸变形过程中微观结构的演化规律,采用共同邻域分析法(common neighbor analysis,CNA)[25]分析原子的局部晶体结构.在使用CNA 分析GR/Mg复合材料的结构时,分别用红色、蓝色、绿色和灰色分别代表HCP 结构原子、体心立方(body centered cubic,BCC)结构原子、FCC 结构原子、无序结构原子和碳原子.

3 结果与讨论

3.1 石墨烯对GR/Mg 复合材料力学性能的影响

为了研究石墨烯对金属镁力学性能的影响,图2 给出了具有不同石墨烯嵌入高度的GR/Mg复合材料的应力-应变曲线.众所周知,材料的应力-应变曲线可以反映材料在载荷作用下的整体力学响应.从图2 可以看出,纯镁和GR/Mg 复合材料的应力-应变曲线均分为三个阶段,且它们的整体变化趋势相似.对于所有模型来说,应力在曲线的开始阶段随应变线性增加,服从胡克定律.应力-应变曲线初始弹性阶段的斜率为材料的杨氏模量.从图2 可以看出,相比于纯镁来说,GR/Mg 复合材料的杨氏模量和第一峰值应力分别提高了大约27.5%和36.5%,这主要是因为石墨烯的杨氏模量和峰值应力(423.17 GPa 和102 GPa)均比单晶镁所对应的值(0.49 GPa 和1.7 GPa)要高很多.研究也指出,石墨烯嵌入位置对GR/Mg 复合材料的杨氏模量和峰值应力的影响较小.当材料的应力达到第一峰值后,随着应变的进一步增大,应力急速下降,表明材料进入塑性变形阶段.在塑性变形阶段,纯镁的流动应力明显比GR/Mg 复合材料的平均流动应力要低,如图2 所示.也就说是,无论石墨烯嵌入高度如何改变,石墨烯的引入都可以明显增强金属镁的力学性能,这主要由于石墨烯具有较高的杨氏模量、屈服应变和屈服强度.从图2 也可以观察到,纯镁和GR/Mg 复合材料的应力达到第一峰值应力之后,随着应变的继续增加,应力都重新呈现上升的趋势,出现了应变强化现象.在应力再次达到峰值之前,GR/Mg 复合材料的应力-应变曲线几乎重合,不依赖于石墨烯的嵌入位置.当应变继续增加,达到约0.18 时,纯镁和GR/Mg 复合材料的应力均达到第二次峰值应力.在经历一个较小的应力下降之后,所有模型的应力均再次开始上升,标志着材料又一次进入了应变强化阶段.从图2可以看出,GR/Mg 复合材料在该应变强化阶段的应力-应变曲线随着石墨烯嵌入高度的不同开始发生了偏移.上述研究结果表明,石墨烯嵌入位置只是在第二峰值应力之后才对GR/Mg 复合材料的塑性变形行为有较大的影响.

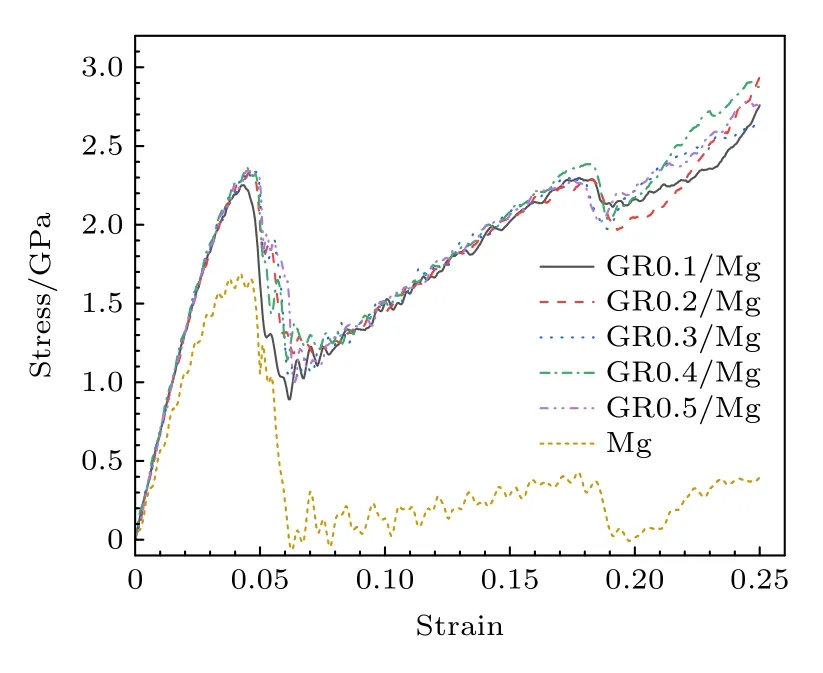
图2 GR/Mg 复合材料和纯镁的应力应变曲线Fig.2.The stress-strain curves of GR/Mg composites and pure magnesium.

为了阐明石墨烯在GR/Mg 复合材料塑性变形过程中所发挥的作用,图3 给出了GR0.5/Mg复合材料在拉伸过程中嵌入石墨烯和镁基体各部分的应力-应变曲线.从图3(a)可以看出,镁基体的屈服应力和屈服应变分别为1.69 GPa 和0.045.然而,嵌入的石墨烯在GR/Mg 复合材料拉伸过程中的屈服应力和屈服应变大约为93.35 GPa 和0.18,如图3(b)所示.也就是说,石墨烯的屈服应力和屈服应变均远大于镁基体对应的屈服值.研究发现,嵌入的石墨烯在所施加的应变范围内并未出现碳-碳键的断裂.此外,从图3(b)也可以看出,石墨烯在应变达到0.18 之后,其应力趋于一稳定的值.因此,GR/Mg 复合材料应力-应变曲线的波动趋势主要受镁基体变形行为的影响,特别是应变0.18 以后的塑性变形曲线,这从图2 也可以看出,单晶纯镁的应力-应变曲线的变化趋势与GR/Mg 复合材料在定性上是一致的.

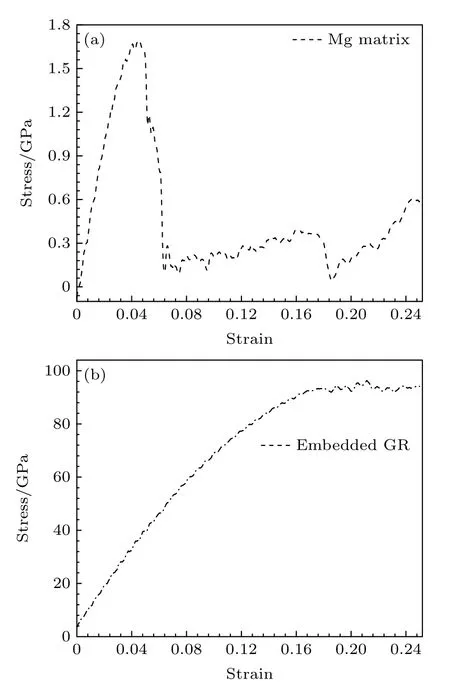
图3 GR0.5/Mg 复合材料在拉伸过程中镁基体 (a)和嵌入石墨烯 (b)的应力-应变曲线Fig.3.The stress-strain curves of magnesium matrix (a)and embedded graphene (b) in the GR0.5/Mg composites.

为了研究石墨烯对金属镁塑性变形行为的影响,图4 给出了纯镁在不同应变下的原子结构图.图中FCC 结构原子、BCC 结构原子、HCP 结构原子和其他结构原子分别显示为绿色、蓝色、红色和白色.从图4(a)可以看出,当应变为0.049 时,纯镁中发生了从HCP 到BCC 结构的相变.这主要是由于在本文中载荷方向平行于纯镁的基面,纯镁初始塑性变形阶段难以发生基面滑移,因此纯镁通过HCP 到BCC 的相变这一过程释放了局部集中的应力,从而导致了应力的迅速下降(如图2 所示),这与An 等[26]的研究结果是一致的,这也说明纯镁的相变过程是一个应力驱动的过程.随着应变的逐渐增大,在纯镁的局部区域,越来越多的HCP结构原子转变为BCC 结构原子.当应变增加到0.056 时,此时HCP→BCC 的相变停止,BCC 相中开始形成与原始基体晶粒取向不同的HCP 结构的新晶粒,如图4(b)中圈出部分所示,这与Chen等[27]的研究结果相一致.也就是说,在这个过程中发生了BCC→HCP 的相变.随着应变的继续增大,BCC→HCP 的相变持续进行,导致了BCC 结构的原子逐渐消失.当应变达到0.062 时,BCC 相几乎全部转变为HCP 相,新的HCP 相呈现狭长的带状,部分BCC 原子与无序原子结合组成了新HCP相与基体HCP 相之间的晶界,如图4(c)所示.在新的HCP 相形成的同时,由于新形成的HCP 相的施密特因子较大,因此在新相中出现了大量不全位错滑移留下的堆垛层错的痕迹[28].此后,晶界不断运动,新HCP 相的宽度逐渐增加,HCP 基体逐渐消失.当拉伸应变达到0.185 时,新旧晶粒晶界迁移趋于结束,原始基体逐渐消失,金属镁的应力此时达到第二次峰值,如图4(d)所示.当应变达到0.190 时,如图4(e)所示,晶界相互作用并逐渐消失,导致了部分应力的释放,因此应力出现了较小的下降.随着进一步施加载荷,纯镁第二次进入塑性强化阶段.当应变达到为0.218 时,新晶粒几乎完全取代了原始的晶粒,如图4(f)所示.

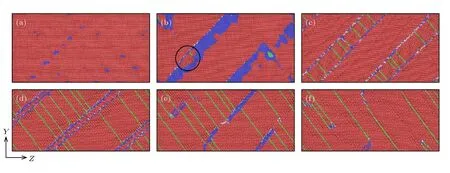
图4 纯镁在不同应变下的原子快照图 (a) ε=0.049;(b) ε=0.056;(c) ε=0.062;(d) ε=0.185;(e) ε=0.190;(f) ε=0.218Fig.4.The atomic snapshots of pure magnesium under different strains:(a) ε=0.049;(b) ε=0.056;(c) ε=0.062;(d) ε=0.185;(e) ε=0.190;(f) ε=0.218.

正如上文所述,GR/Mg 复合材料的应力达到第二峰值以后,其流动应力发生了偏移.为了研究石墨烯嵌入高度对GR/Mg 复合材料在该阶段塑性变形行为的影响,图5 给出了GR/Mg 复合材料的平均流动应力随着石墨烯嵌入高度的变化曲线.本文定义每个模型在第二峰值应力之后的应力平均值为该模型的平均流动应力.从图5 可以看出,GR/Mg 复合材料的平均流动应力首先随着石墨烯嵌入高度的增加而增加,当嵌入高度达到0.4L时,GR/Mg 复合材料平均流动应力达到最高,随后GR/Mg 复合材料的平均流动应力又出现了下降趋势.该研究结果意味着随着石墨烯嵌入位置的变化,GR/Mg 复合材料的镁基体的塑性变形行为可能发生了改变.

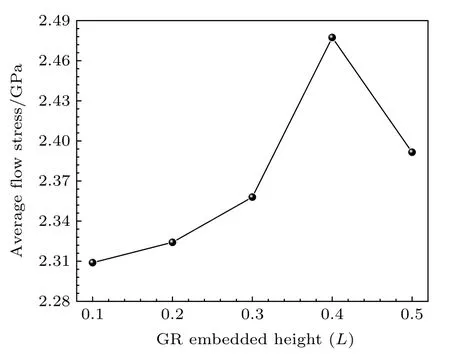
图5 GR/Mg 复合材料的平均流动应力随石墨烯嵌入高度的变化曲线Fig.5.The curve of the average flow stress of the GR/Mg composites with different graphene embedded heights.

同纯镁类似,GR/Mg 复合材料中的镁基体在塑性变形过程中同样产生了HCP→BCC 的相变,且随着拉伸应变的增加,BCC 相中会形成与原始基体晶粒取向不同的新HCP 相.与纯镁不同的是,嵌入的石墨烯将镁基体沿X轴方向分为上下两部分,在塑性变形过程中,取向相同的HCP 结构的新晶粒几乎同时在两部分镁基体中形核,最初生成的HCP 相并未穿透石墨烯,而是在各自部分的镁基体中扩展,这主要是由于嵌入石墨烯的对相变的阻碍作用[29].为了研究GR/Mg 复合材料在第二峰值以后的塑性变形行为,图6(a)—(c)给出了石墨烯嵌入高度分别为0.1L,0.3L,0.5L的GR/Mg 复合材料在应变为0.177 下的原子快照图,其中每个图的上方的图为俯视图,下方的图为侧视图.图中FCC 结构原子、BCC 结构原子、HCP 结构原子和其他结构原子分别显示为绿色、蓝色、红色和白色.从图6 可以看出,当应变达到0.177 时,GR0.1/Mg和GR0.3/Mg 复合材料上半部分新晶粒还在继续扩张,而下半部分中相邻晶界已经开始发生合并,特别是GR0.1/Mg 复合材料,如图6(a)圆圈部分所示.然而,GR0.5/Mg 复合材料上下两部分新晶粒晶界迁移速度基本一致,如图6(c)所示.可见,石墨烯嵌入位置对新晶粒长大有一定影响,嵌入位置距下表面越近,石墨烯下表面的新晶粒晶界的迁移速度越快.

为了阐明GR/Mg 复合材料在第二峰值应力后平均流动应力随石墨烯嵌入高度变化的内在机制,图6(d)—(f)给出了GR0.1/Mg,GR0.3/Mg,GR0.5/Mg 复合材料在应变为0.225 时的原子快照俯视图,其中每个图的上方和下方的图分别对应于复合材料中石墨烯上下两部分镁基体的原子快照图.如图6(d)和图6(e)所示,GR0.1/Mg 和GR0.3/Mg 复合材料下部分镁基体中的FCC 堆垛层错比上部分的更为密集.也就是说,复合材料下部分镁基体更容易发生位错的滑移.然而,当石墨烯插入高度达到0.5L时(此时,上下两部分镁基体的尺寸相同),GR0.1/Mg 复合材料上下部分镁基体中的FCC 堆垛层错排布基本均匀,且数量较少,如图6(f)所示.研究表明,石墨烯不仅对基体中位错滑移和相变产生阻碍,而且石墨烯嵌入位置还会影响复合材料上下两部分镁基体的塑性变形难易程度,嵌入的位置距下表面越近,复合材料下部分越容易发生位错的滑移.也就是说,GR/Mg 复合材料下部分镁基体塑性变形行为对石墨烯嵌入位置的依赖性是复合材料平均流动应力发生转折(如图5 所示)的主要原因.

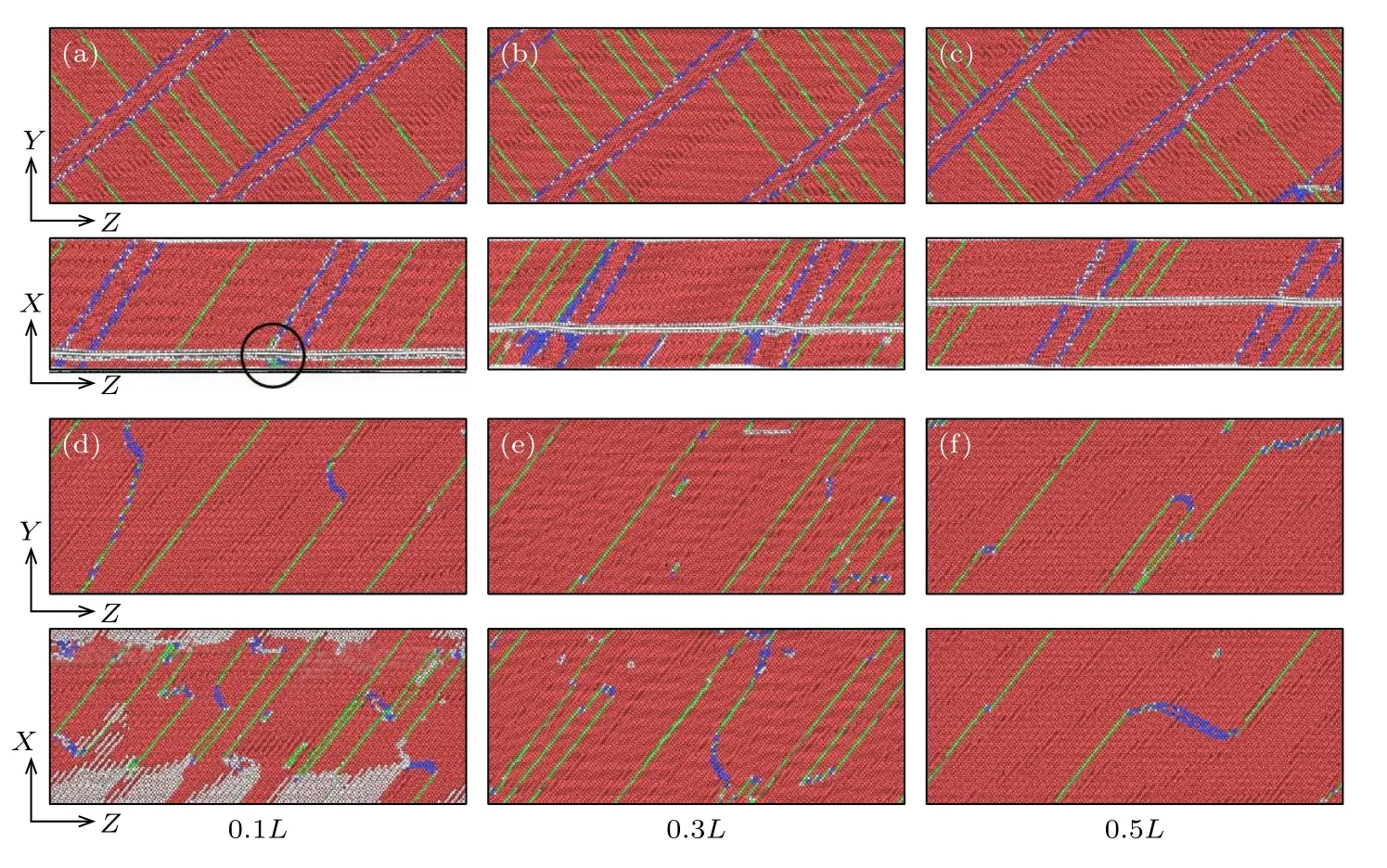
图6 GR/Mg 复合材料在不同应变下的原子快照图Fig.6.The atomic snapshots of the GR/Mg composites at different strains.

为了阐明石墨烯与镁基体之间的相互作用,以GR0.5/Mg 复合材料为研究对象,对其在塑性变形过程中的塑性变形细节进行了分析.图7(a)和图7(b)给出了GR0.5/Mg 复合材料在不同应变下的位错分析图.从图7(a)和图7(b)可以看到,当应变达到0.056 时,在镁基体中的石墨烯界面附近出现了位错的形核和滑移,但随着应变的增加,位错仅在镁基体的上下两部分晶体内进行运动,并未穿过石墨烯,石墨烯对位错的运动显示了明显的阻碍效果.图7(c)和图7(d)给出了GR0.5/Mg 复合材料在不同应变下BCC 结构相分布图.从图7(c)和图7(d)可看出,当应变达到0.051 时,镁基体上下两部分中均产生了HCP→BCC 的相变,但基体中产生的BCC 相被石墨烯阻隔,HCP→BCC 的相变同样只能在各自的区域内进行,表明石墨烯对镁基体中相变过程具有阻碍作用.应该指出的是,GR0.5/Mg 复合材料在塑性变形过程中,HCP→BCC的相变和位错滑移是同步进行的,如图7 所示.

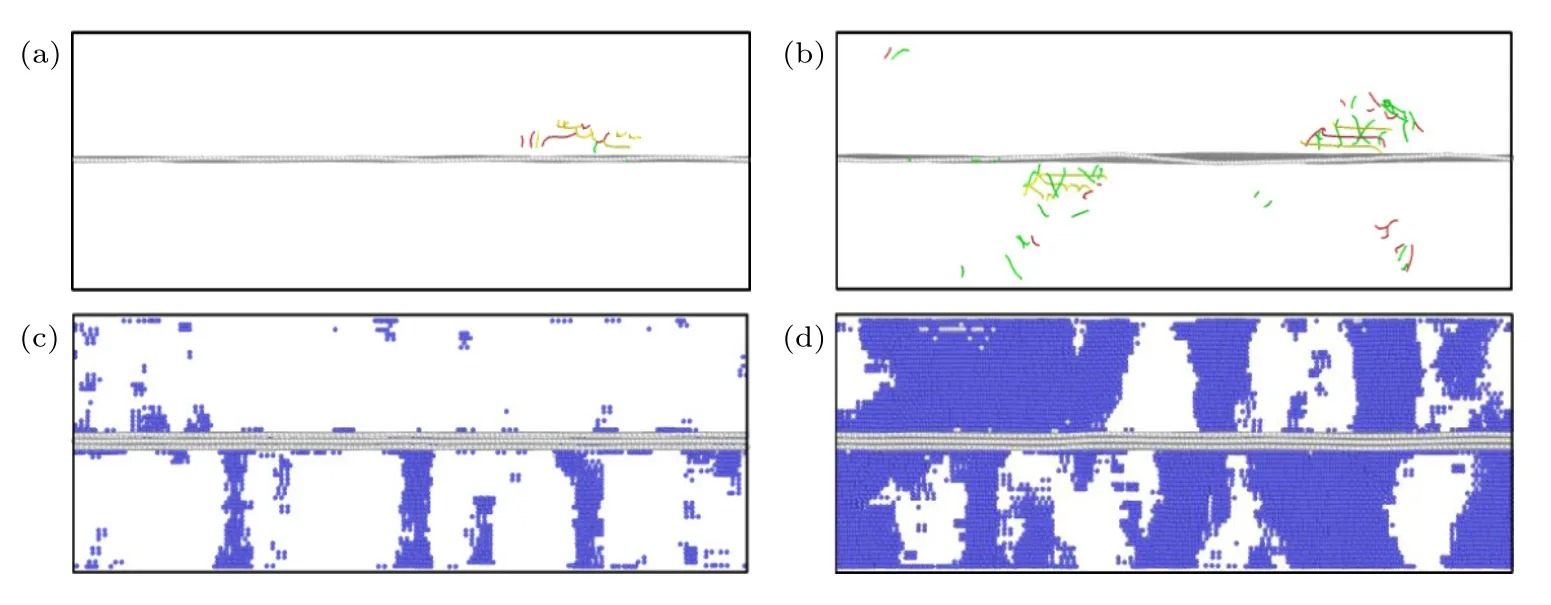
图7 GR0.5/Mg 复合材料在不同应变下的结构快照图 (a) ε=0.056;(b) ε=0.062;(c) ε=0.051;(d) ε=0.056Fig.7.The structure snapshots of the GR0.5/Mg composites at different strains:(a) ε=0.056;(b) ε=0.062;(c) ε=0.051;(d) ε=0.056.

此外,选取石墨烯插入高度为0.5L的模型,研究了石墨烯Y方向的尺寸对GR/Mg 复合材料力学行为的影响,这里选择的石墨烯的尺寸分别为5.11 和10.22 nm.图8 给出了不同石墨烯尺寸的GR0.5/Mg 复合材料的应力应变曲线.研究结果表明,GR/Mg 复合材料的杨氏模量、屈服强度和塑性流动应力均随着石墨烯尺寸的增大而增大.这一方面是由于高性能石墨烯的含量增大,根据复合材料混合定律,GR/Mg 复合材料的力学性能会增强;另一方面随着石墨烯尺寸的增大,石墨烯阻碍镁基体中相变扩展和位错滑移的面积越大,从而能够更好地增强GR/Mg 复合材料的力学性能.从图8 也可以看出,GR/Mg 复合材料应力应变曲线的变化趋势几乎相同,不依赖于嵌入的石墨烯的尺寸,也就是说石墨烯尺寸并没有改变GR/Mg 复合材料塑性变形机制.

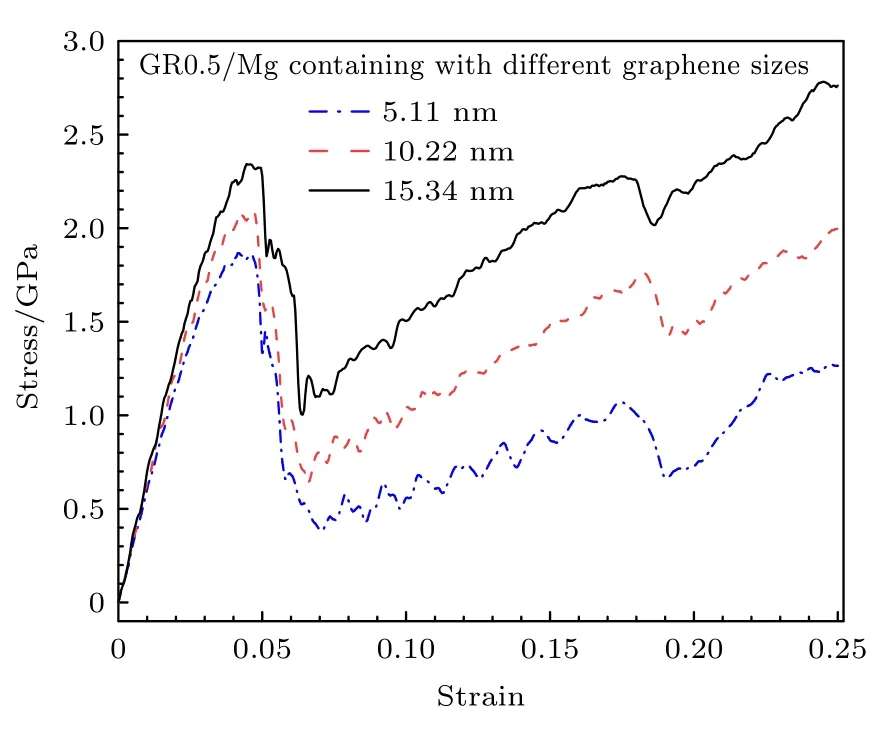
图8 不同石墨烯尺寸的GR0.5/Mg 复合材料及纯镁的应力应变曲线Fig.8.The stress-strain curves of the GR0.5/Mg composites with different graphene sizes and pure Mg.

3.2 镁基体的相变机制

为了揭示GR/Mg 复合材料在塑性过程中HCP 和BCC 相之间的相变机制,图9 给出了镁基体HCP→BCC 相变的原理图.图9(a)用黑线表示HCP 单位晶格,用红色原子表示HCP 晶格单元中的上下底面的原子,蓝色原子表示晶胞内中间层原子.HCP 结构的(0001)基面按照...ABABAB...的方式堆垛.在加载过程中,基面上的原子首先发生了重排,晶格夹角从最初的60°转变到70.5°,如图9(b)和图9(c)所示.随后,HCP 结构的基面变形为非等边六边形,其中A 层原子被拉伸,而B 层原子向A 层原子运动形成的菱形中心移动,最终演变为BCC 结构的(110)面,如图9(d)—(f)所示.复合材料在塑性变形后期,其第一次相变产物BCC 相的(101)面在应力驱动下转变为HCP 相的(0001)面,从而发生了HCP→BCC 相变的逆过程(BCC→HCP 相变).为了比较两次相变导致的镁基体位向的变化,图9(g)给出了GR0.5/Mg 复合材料在应变为0.059 的局部原子结构图,其中方形框内为放大部分为镁基体中HCP 转变为BCC相的原子图,圆形框则显示了BCC 转变为HCP相的原子图.为方便起见,将最初的镁基体HCP相定义为α1-Mg,HCP→BCC 相变后的BCC 相定义为β-Mg,而将BCC→HCP 相变后的HCP 相定义为α2-Mg.从图9(g)可以看出,α1-Mg 和β-Mg 的取向关系为(0001)HCP||(110)BCC,而β-Mg与α2-Mg 的取向关系为(101)BCC||(0001)HCP,这与An 等[30]的研究结果一致.因此,GR/Mg 复合材料经过HCP→BCC→HCP 的相变,α2-Mg 新晶粒的基面与原始α1-Mg 基体的基面之间形成了约121.5°的夹角,与拉伸方向形成了58.5°的夹角,因此其施密特因子增大,从而有利于位错的成核与滑移.

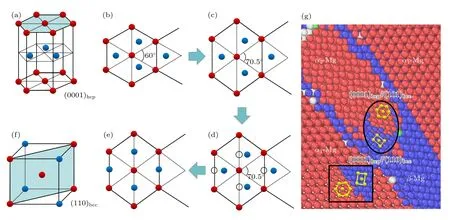
图9 (a)—(f) 镁基体中HCP→BCC 相变的原理图;(g) GR0.5/Mg 复合材料在0.059 应变下的原子结构图Fig.9.(a)–(f) The schematic diagram of phase transformation of HCP→BCC in magnesium matrix;(g) the GR0.5/Mg composite with BCC structure at strain 0.059.

4 结论

本文采用分子动力学模拟方法研究了GR/Mg复合材料在拉伸载荷下的力学行为,分析了石墨烯嵌入位置对GR/Mg 复合材料力学性能和塑性变形行为的影响.研究发现,石墨烯的嵌入显著提升了金属镁的力学性能,相比于纯镁来说,GR/Mg复合材料的杨氏模量和第一峰值应力分别提高了约27.5%和36.5%,这主要是因为石墨烯具有很高的杨氏模量和峰值应力.研究表明,石墨烯嵌入位置对GR/Mg 复合材料的杨氏模量和峰值应力的影响较小,但会明显影响GR/Mg 复合材料第二峰值应力之后的塑性变形行为.GR/Mg 复合材料塑性变形后期的平均流动应力首先随着石墨烯嵌入高度的增加而增加,当嵌入高度达到0.4L时,平均流动应力达到最高,随后又出现了下降趋势.GR/Mg复合材料呈现的这种现象可以从石墨烯上下两部分镁基体的塑性变形行为得到解释,当石墨烯嵌入高度较小时,GR/Mg 复合材料的下部分镁基体塑性变形能力较强(下部分镁基体中出现了大量不全位错滑移留下的堆垛层错的痕迹),而当石墨烯嵌入高度较大时,GR/Mg 复合材料上下两部分镁基体的塑性变形能力相当,上下两部分镁基体趋向于发生较为同步的塑性变形行为.研究也指出,在本文的载荷条件下,镁基体在塑性变形过程中均发生了从HCP 到BCC 再到HCP 结构的相变,且该变形行为不依赖于石墨烯的嵌入位置.最后,本文对镁基体的相变机制也进行了详细分析.本文所得结果可为设计高性能的石墨烯金属基复合材料提供先期的科学预测和有益借鉴.