基于CV-RMMP重构算法的水声稀疏信道估计

张海霞,杜子俊,王景景

(青岛科技大学 信息科学技术学院,山东 青岛 266061)

声波在水下环境中具有良好的传播特性,是目前应用最广泛的水下通信方式。但水声通信存在可用带宽有限、传播时延大、多径衰落等问题[1-3]。正交频分复用(orthogonal frequency division multiplexing,OFDM)将信道划分为若干正交子信道进行信息传输,提高了数据传输速率与频谱利用率[4-6],成为高速水声数据传输研究热点之一。信道估计技术可以通过估计信道状态信息提高接收端数据解调的正确率,对OFDM水声通信系统具有关键作用。但由于水下信道复杂,要完成信道估计需要大量子载波传输导频信息,造成频谱资源严重浪费。

压缩感知(compressed sensing,CS)理论打破了奈奎斯特采样定理的局限性,它提出当信号在某个域中稀疏[7-9]时,可以使用更少的采样点来准确地重建稀疏信号。由于水声信道具有稀疏性[10-11],将压缩感知用于水声信道估计可通过少量导频数据就能估计出信道参数,从而提高频谱利用率,基于CS的水声信道估计也引起了学者的重视。重构算法是压缩感知的关键技术,目前已有的重构算法主要包括凸优化类算法、组合优化类算法和贪婪迭代类算法。其中贪婪迭代类算法效率较高且较易实现,更适用于对实时性要求较高的水声信道估计。匹配追踪(matching pursuit,MP)算法与正交匹配追踪(orthogonal matching pursuit,OMP)算法都是经典的贪婪迭代算法[12-13],其基本思想是迭代地找到信号的支撑集,每次迭代会从词典中选择与残差信号最匹配的一个原子。但这种单个候选集的选择模式存在缺陷,会使问题陷入局部最优解。有学者提出了多路径匹配追踪(multipath matching pursuit,MMP)算法,在每次迭代中选择不同原子放入多个候选集中,提高了算法的重构性能[14],但也增加了算法的复杂度。大多数贪婪算法需要准确知道信道稀疏度才能正确停止迭代,但是在大多数实际情况下无法满足要求。稀疏度自适应匹配追踪(sparsity adaptive matching pursuit,SAMP)算法提出了一种不需要稀疏度的算法,但仍需知道信道噪声水平才能设置合适阈值来停止迭代[15],且该阈值设置对算法重构精度影响很大。

针对上述算法对信道先验信息(例如稀疏性或噪声级别)依赖性和复杂度高的问题,本工作提出一种基于交叉验证[16-17]与正则化[18]相结合的多径匹配追踪算法(multipath matching mursuit based on cross validation and regularization,CV-RMMP)算法,将其用于水声稀疏信道估计。

1 系统模型

水声信道是一个时变多径信道,其信道冲击响应为

其中,C为水声信道中多径数目,Ai(t)和τi(t)分别表示t时刻第i条路径的复增益和时延。水声信道可以看作频率选择性慢衰落信道,此时信道的相干时间远大于OFDM符号周期,可以认为在一个或几个OFDM符号内信道是时不变的。式(1)可表示为

对h(τ)以系统采样周期Ts采样得离散时不变信道模型为

其中,M为信道长度。水声信道的稀疏性即体现在[h0,h1,…,h M－1]中非零元素个数很少,其非零值个数K(K≪M)即为此信道稀疏度。假设系统有N个子载波,发送信号经过水声信道后得到的系统传输模型矩阵形式可表示为

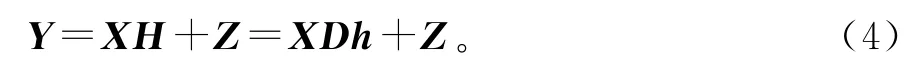
其中,矩阵X＝diag(x(0),x(1),…,x(N－1))表示OFDM符号携带的数据,Y＝[Y(0),Y(1),…,Y(N－1)]T为接收的数据符号,H＝[H(0),H(1),…,H(N－1)]T为信道频域响应,Z＝[Z(0),Z(1),…,Z(N－1)]T为高斯白噪声,D为N×M维的DFT变换矩阵,表示如下

在OFDM系统的接收端,接收到的导频信号用于信道估计。假设发送端插入导频数量为P,则接收端接收导频信号可表示为

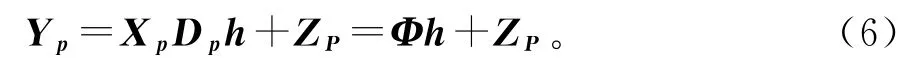
Yp为接收到的P×1维观测向量,Φ＝XpDp为P×M维测量矩阵,Yp,XP,FP在接收端均为已知。由于信道的稀疏性,h中的多数成分为零,非零项代表不同时延的幅度值。估计这个信道就是找出这些时延并计算这些非零值的大小,信道估计问题就转为在获取观测向量Yp和已知训练序列构成的测量矩阵Φ的情况下,利用合适的重构算法重构出未知的水声信道时域冲激响应h。

2 基于CV-RMMP算法的水声信道估计

本工作对MMP算法的稀疏度依赖和复杂度方面进行了优化,提出了一种CV-RMMP重构算法并将其用于稀疏水声信道估计。

2.1 MMP算法

在传统贪婪迭代算法中,每次迭代仅选择一个原子。如果在一次迭代过程中选择了错误的原子,则接下来的迭代过程都是基于此错误的选择,所得最终支撑集将是错误的。MMP算法则选择多个候选集,并在迭代完成后,基于残差最小化在所有候选集中选出最终支撑集,此策略增大了搜索范围,提高了原子被正确选择的概率,比传统单个候选集的选择模式精度更高。MMP算法步骤如图1所示。

图1 MMP算法Fig.1 MMP algorithm

其中K为稀疏度,k为迭代索引,J是每个候选集的候选路径数,为第k次迭代候选集的集合,为第k次迭代的第i个候选集,表示第k次迭代的第i个候选集的h估计值,表示第k次迭代时第i条路径的残差。

2.2 CV-RMMP算法

2.2.1 正则化

由图1中的迭代步骤可知,MMP算法的每一次迭代过程中,都会选择J个原子分别放入不同候选集中,如多叉树一样,在每次迭代中基于根节点分出多个子节点,这种方式比单个候选集的原子选择模式可靠性更高,但计算复杂度也随之上升。因此,本文采用一种基于正则化删除部分候选路径并约束候选集数量的方式降低复杂度。

对于第k次迭代的第i条路径,通过求残差rk－1i与测量矩阵Φ的每个原子(Φ的列向量)的内积绝对值,来计算相关系数:

首先在集合Γ中寻找满足条件的子集Ωk:

然后在Ωk中寻找具有最大能量的集合Ωmax:

Ωmax本质为Γ的子集,用Γ*表示,与Γ相比,Γ*通过正则化删除部分相关性小的原子,在保证重建性能的前提下降低了计算复杂度和存储开销。此外,如图2所示,通过设置最大候选集数量Nmax来进一步降低复杂度。

2.2.2 交叉验证

根据交叉验证的理论[16-17],将接收向量YP分为重建向量和交叉验证向量。测量矩阵Φ也被分成两个子矩阵,即Pre×M维重构矩阵Φre和Pcv×M维交叉验证测量矩阵Φcv,其中P＝Pcv＋Pre。相应的得到一个重建方程

和一个交叉验证方程

式(10)用于贪婪算法重建稀疏信号,式(11)用于确定停止条件。其中。矩阵Φ由Φre和Φcv组成。对于稀疏的水声信道,是未知的K稀疏信道向量。使用表示第k次迭代中的估计信道矢量,则第k次迭代中的CV残差表示为

当不使用交叉验证时,第k次迭代的残差定义为

图2 CV-RMMP算法Fig.2 CV-RMMP algorithm

图2为提出的CV-RMMP算法详细步骤。如步骤1所示,在使用交叉验证时,无需根据信道稀疏度或噪声级别设置最大迭代次数或重构阈值,而仅需要最大迭代次数即可。通常可以将Ncv的值设置为大于稀疏K的值,实际应用中可以通过使用同步帧来粗略地估计该设置值。

如图2中步骤4,CV-RMMP算法首先利用2.2.1节介绍的正则化得到集合Γ*,相比于 图1 MMP算法中的集合Γ,通过引入正则化对已选索引值进行二次筛选,删除部分能量小的路径,在保证重建性能的前提下降低了计算复杂度和存储开销。根据2.2.2节介绍的交叉验证原理,将MMP算法中的接收向量YP分为重建向量和交叉验证向量;将测量矩阵Φ分为重构矩阵Φre和交叉验证测量矩阵Φcv。利用重建向量和重构矩阵进行迭代估计,第k次迭代完成后得到相应的估计值,之后利用和交叉验证向量以及交叉验证矩阵计算第k次迭代的CV残差,如步骤20。Ncv次迭代结束后选出最小CV残差,此残差对应的迭代次数记为kcv,找到第kcv次迭代对应的信道估计值,即为所求最终信道估计值。

3 仿真结果及分析

在本节中,将研究本工作所提出的CV-RMMP算法的性能并将其与其他估计算法的性能进行比较。首先,通过BELLHOP软件仿真生成信道冲激响应,表1给出了主要仿真参数,其中海洋环境参数参考冬季浅海设置。OFDM系统的参数如下:子载波的数量N＝512;导频的数量为P＝128,插入方式为随机插入导频;调制方式采用16QAM。对MMP和CV-RMMP算法,设置J＝5,Pcv＝30,Nmax＝50。使用MATLAB R2018a在由2.90 GHz Intel Core i5 CPU和4 GB内存的计算机上进行仿真。

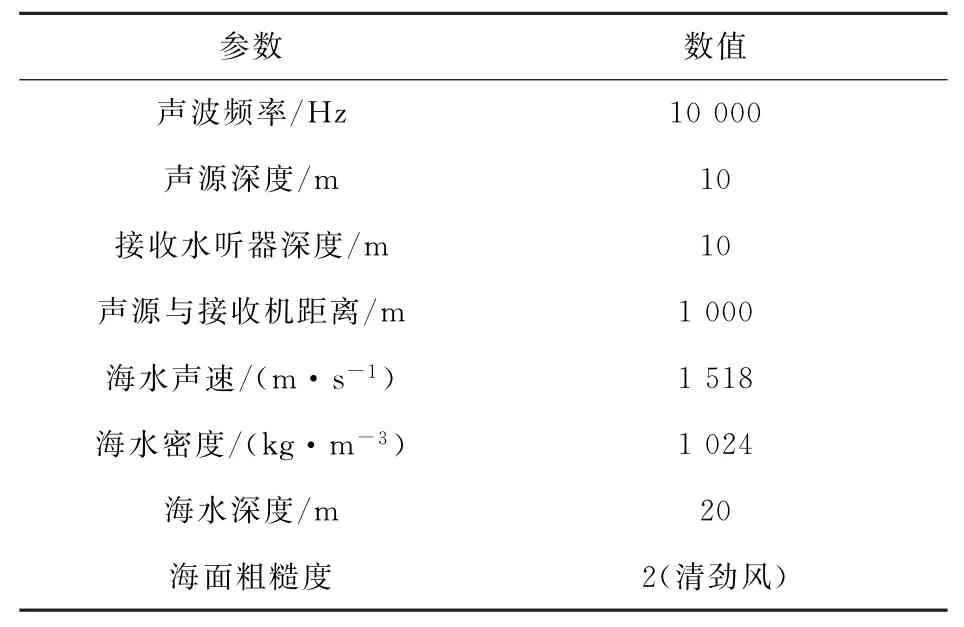
表1 BELLHOP仿真主要参数Table 1 Main parameters of Bell Hop simulation

OMP为经典贪婪迭代算法,该算法需要准确知道信道稀疏度才能正确停止迭代;SAMP算法在OMP算法基础上,通过设置合适的阈值和步长来确定迭代停止条件,该算法虽然不需要稀疏度,但仍需知道信道噪声水平才能正确停止迭代;上述两种算法均为单候选集的原子选择模式,容易陷入局部最优,MMP算法通过选择多个候选集方式解决此问题并提高了算法估计精度,但仍存在稀疏度依赖和复杂度高的问题;本研究提出的CV-RMMP算法通过结合交叉验证和正则化对MMP算法进行优化,可以使算法在未知稀疏度情况下恢复稀疏信号。为了验证所提算法在水声信道估计中的估计性能,如图3和图4所示,本研究分别比较了4种算法在稀疏度K＝7和K＝15两种情况下不同重构算法的误码率(BER)。可以看出,在两种情况下,随信噪比增加所有算法的误码率降低。在相同的信噪比下,CV-RMMP和MMP表现出了最好的误码率性能,而SAMP算法的最低。尽管CV-RMMP算法不需要关于稀疏度K的先验信息,但仍能达到与MMP算法相近的重构性能。此仿真证明CVRMMP算法具有很高的鲁棒性,可以恢复稀疏信号,而无须事先了解稀疏度和噪声水平等先验信息。

图3 SAMP、OMP、MMP和CV-RMMP算法BER比较(K＝7)Fig.3 SAMP,OMP,MMP and CV-RMMP algorithm BER comparison(K＝7)

图4 SAMP、OMP、MMP和CV-RMMP算法BER比较(K＝15)Fig.4 SAMP,OMP,MMP and CV-RMMP algorithm BER comparison(K＝15)

图5为信噪比20 dB、K＝7情况下,随迭代次数增加,重构误差、残差ε和CV残差εcv的变化。可以看出,残差单调递减,因此在没有事先了解稀疏度和噪声水平的情况下无法确定停止迭代的时间,所以残差不能用作正确终止算法的指标。同时,CV残差与重构误差具有相同的趋势,都在Ncv＝7处取得最小值。所以CV-RMMP算法可以根据CV残差得到重构信号,该仿真进一步验证了CV的合理性。

图5 重构误差σ、残差ε和CV残差εcv随最大迭代次数Ncv的变化Fig.5 Reconstruction errorσ,residualε,and CV residualεcv change with the maximum number of iterations Ncv

本工作以算法估计一次水声信道的平均运行时间代表算法的计算复杂度,表2给出了在信噪比20 dB、K＝7情况下SAMP、OMP、MMP和CVRMMP算法平均运行时间,其中SAMP步长为4。可以看出,MMP算法复杂度远高于OMP算法,这是由于其基于多个候选集的原子选择模式导致的。CV-RMMP算法的仿真时间低于MMP算法,这是由于CV-RMMP算法通过正则化和限制候选集数两个策略降低了MMP算法的计算复杂度,但优化后的算法仍存在多个候选集,所以在时间复杂度上要高于单候选集的OMP算法。

表2 SAMP、OMP、MMP和CV-RMMP算法平均运行时间比较Table 2 Comparison of average running times of SAMP,OMP,MMP and CV-RMMP algorithms

4 结 语

本工作结合水声信道具有稀疏性的特点,通过对水声OFDM通信系统的分析,提出了一种高度实用的CV-RMMP算法。该算法利用交叉验证确定迭代停止条件,无需事先了解信道稀疏度或噪声水平就可以重建信号;引入正则化来进一步筛选候选集,降低了算法的复杂性及存储开销。仿真实验表明,CV-RMMP算法优于现有的OMP算法和SAMP算法。可在未知信道稀疏度的情况下,以更少的重构时间达到与MMP相似的重构性能。