基于观测器的时滞离散时间马尔可夫跳变系统有限时间H∞控制
2022-04-27魏雪雪刘凝哲刘西奎李艳
魏雪雪,刘凝哲,刘西奎,,李艳
(1. 山东科技大学 数学与系统科学学院, 山东 青岛 266590;2.中国矿业大学(北京) 机电与信息工程学院, 北京 100083;3.山东科技大学 电气信息系,山东 济南 250031)
马尔可夫跳变系统(MJSs)是一类由多个子系统组成的混合系统,每一个模态对应一个确定的子系统,模态间的切换由马尔可夫随机过程决定[1-6]。MJSs可以用来建模具有结构突变的动力学系统,在实际中有着广泛的应用,如Dong等[7]研究了具有传感器饱和的离散时间马尔可夫跳变系统的故障检测问题;Shi等[8]利用李雅普诺夫函数理论和凸多面体技术,研究了不确定离散时间奇异MJSs的故障检测滤波器设计问题;Liu等[9]提出了一种新的基于动态输出反馈的异步控制器,研究了网络化MJSs的异步H∞控制问题。此外,MJSs在网络[10-12]、采样[13-15]、滑模[16-18]、容错[19-21]等控制系统中也有着重要的应用。对于MJSs,其稳定性研究是一项最基本的问题。然而,由于时滞广泛存在于各种系统之中,导致系统性能变差,甚至不稳定。因此,具有时滞的MJSs引起了学者的广泛关注,取得了众多的研究成果,如Du等[22]研究了具有时滞的MJSs的异步控制方法;Zhuang等[23]研究了带有时变时滞的中立型MJSs的非脆弱时滞反馈控制问题;Fang等[24]通过设计一种新型的切换滑面函数,研究了带有时滞的非线性MJSs的滑模控制问题;更多关于时滞MJSs的研究成果可见文献[25-29]。
众所周知,李雅普诺夫稳定性理论研究无限时间间隔上系统的渐近稳定性。然而,在许多实际应用中,需要更加关注系统在有限时间间隔内的暂态性能,例如,过大的瞬时电压会对电力系统造成损坏[30];海浪会对欠驱动船舶的航向角造成影响,使得船舶偏离预设路径[31];扰动会影响有限时间内航天器的姿态[32]。基于上述类似问题,Dorato[33]在1961年首次提出有限时间稳定(finite-time stability,FTS)这一概念。不同于李雅普诺夫意义下的稳定性,FTS描述的是有限时间区间上系统的暂态性能,即在固定的时间间隔内,系统的状态不会超过某个确定的阈值,已经取得许多关于FTS的研究成果[34-38]。在实现系统FTS后,需要抑制干扰对系统的影响,而H∞控制可以解决此问题。因此,学者在FTS的基础上又引入了H∞控制,以确保闭环系统有限时间稳定且干扰满足一定的抑制水平,从而得到了有限时间H∞有界的概念。如Chen等[39]研究了具有区间时变时滞的离散时变系统的有限时间H∞控制问题,Ju等[40]研究了事件触发下线性中立半马尔可夫跳变系统的有限时间H∞控制问题,Liu等[41]研究了状态相关不确定系统的有限时间H∞滤波问题。虽然已经取得许多有限时间H∞控制的研究结果,但是对于离散时间马尔可夫跳变系统(DMJSs)的有限时间H∞控制问题有待研究,这是本文研究的主要内容。
此外,上述的研究成果都是在假设系统状态可测量的情况下进行的,然而在实际中,由于技术、成本等因素的影响,系统的状态不一定可以完全得到。而基于观测器的控制器则可以克服此困难,所以最近几年,基于观测器的控制方法受到了学者的广泛关注。如Tan等[42]研究了量化和随机网络攻击下基于观测器的互联模糊系统的有限时间H∞控制问题,Gao等[43]研究了基于观测器的不确定离散时间非齐次马尔可夫跳变系统的有限时间H∞控制问题,Zhang等[44]研究了基于观测器的离散时间齐次马尔可夫跳变系统的有限时间H∞控制问题。然而,鲜有文献对基于观测器的DMJSs的有限时间H∞控制问题进行研究。本文将考虑基于观测器的时滞DMJSs的有限时间H∞控制问题,即设计基于观测器的状态反馈控制器使闭环误差系统有限时间有界且满足规定的干扰衰减水平。
1 定义和系统描述
记号:Rn,Rn×m,N分别表示n维实向量,n×m维实矩阵和非负整数集;A>0(A<0)表示A是正定(负定)矩阵;E{·}表示某种概率测度P的数学期望;*表示矩阵中的对称项;diag{…}表示块对角矩阵;σmin(A)和σmax(A)分别表示矩阵A的最小和最大特征值;MT和M-1分别表示矩阵M的转置和逆矩阵。如果矩阵的维数没有说明,则认为矩阵与代数运算是相容的。
考虑如下时滞DMJSs:
x(k+1)=A1(rk)x(k)+Ad1(rk)x(k-d)+
B1(rk)u(k)+C1(rk)v(k)+[A2(rk)x(k)+
Ad2(rk)x(k-d)+B2(rk)u(k)+
C2(rk)v(k)]w(k),
(1)
y(k)=D(rk)x(k)+G(rk)u(k),
(2)
z(k)=D1(rk)x(k)+Dd(rk)x(k-d)+
G1(rk)u(k)+G2(rk)v(k),
(3)
x(n)=φ(n),n∈{-d,…,0},
(4)
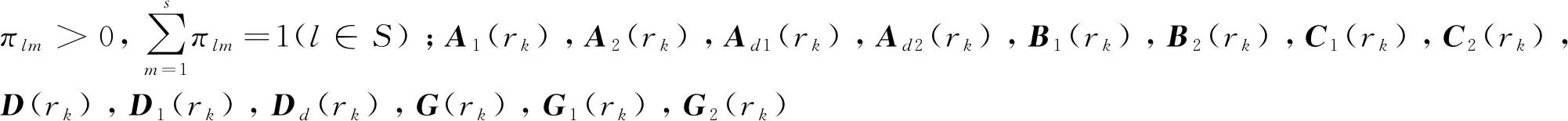
外部干扰v(k)满足
(5)
定义如下基于观测器的状态反馈控制器:
(6)
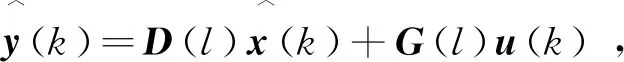
(7)
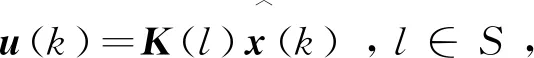
(8)
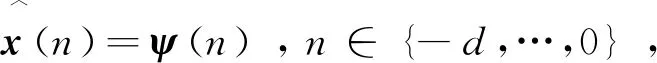
(9)
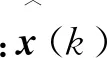
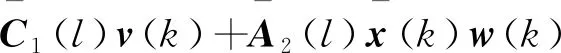
(10)
G2(l)v(k),
(11)
式中
定义1如果系统(10) (u(k)=0,v(k)=0)满足
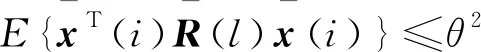
(12)
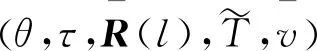
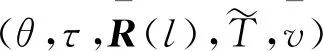
(13)
引理1(舒尔补引理)[45]对于实矩阵N,MT=M,RT=R>0,有
本文的主要目的是设计一个形如式(6)—(9)的基于观测器的状态反馈控制器,保证闭环误差DMJSs (10)和(11)有限时间H∞有界。
2 有限时间H∞控制分析
本节讨论系统(1)—(4)的基于观测器的有限时间H∞控制问题,以线性矩阵不等式的形式给出闭环误差系统(10)和(11)有限时间有界,且控制输出z(k)和外部干扰v(k)满足条件(13)的充分条件。
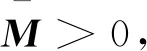
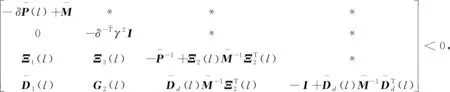
(14)
(15)
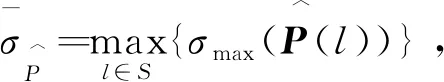
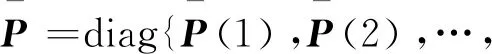
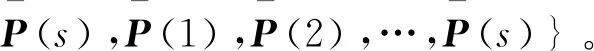
证明定义如下Lyapunov-Krasovskii函数
经计算,可得
V(k+1,rk+1=m)-V(k,rk=l)=
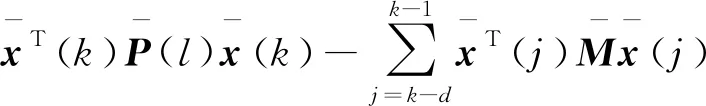

(16)
其中
根据引理1,可以证明条件(14)等价于
<0。
(17)
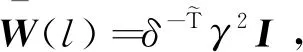
(18)
对条件(18)应用引理1,可以得到

(19)
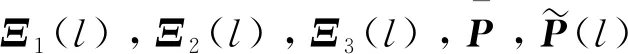
<0。
(20)
根据条件(16)和(20),得
E{V(k+1,rk+1=m)-V(k,rk=l)}<
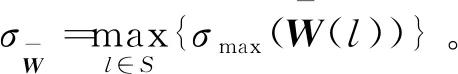
从而
E{V(k+1,rk+1=m)}<δE{V(k,rk=l)}+
(21)

E{V(k)}<δkE{V(0,r0=h)}+
(22)
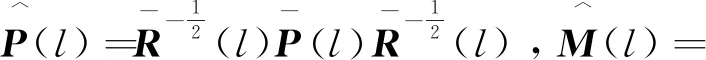
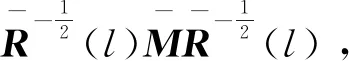
i∈{-d,…,0} ,则
(23)
(24)
根据条件(22)—(24),得
由条件(15)可得
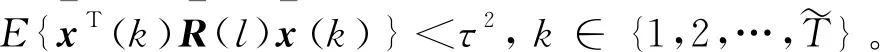
考虑上述Lyapunov-Krasovskii函数,则有
E{V(k+1,rk+1=m)}<δE{V(k,rk=l)}-
(25)
E{V(k,rk=l)}<δkE{V(0,r0=h)}-
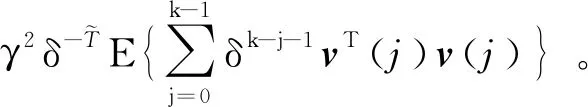
(26)
因为V(k,rk=l)≥0,k∈N,在零初始条件下,根据条件(26)可以得到
(27)
又δ≥1,根据条件(27)
(28)
注1当w(k)=0时,定理1即为文献[44]的定理3;当w(k)=d=0时,定理1即为文献[43]的定理2。
3 有限时间H∞控制器设计
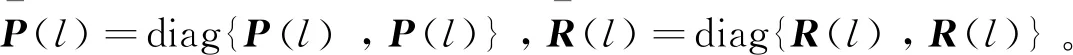
定理2考虑时滞DMJSs(10)和(11),如果存在标量δ≥1,η>0,τ>0,ξ1>0,ξ2>0,γ>0, 矩阵J>0,正定矩阵X(l),矩阵Y(l)、F(l)和非奇异矩阵Z(l),对任意l∈S,使得下式成立
D(l)X(l)=Z(l)D(l),
(29)
(30)
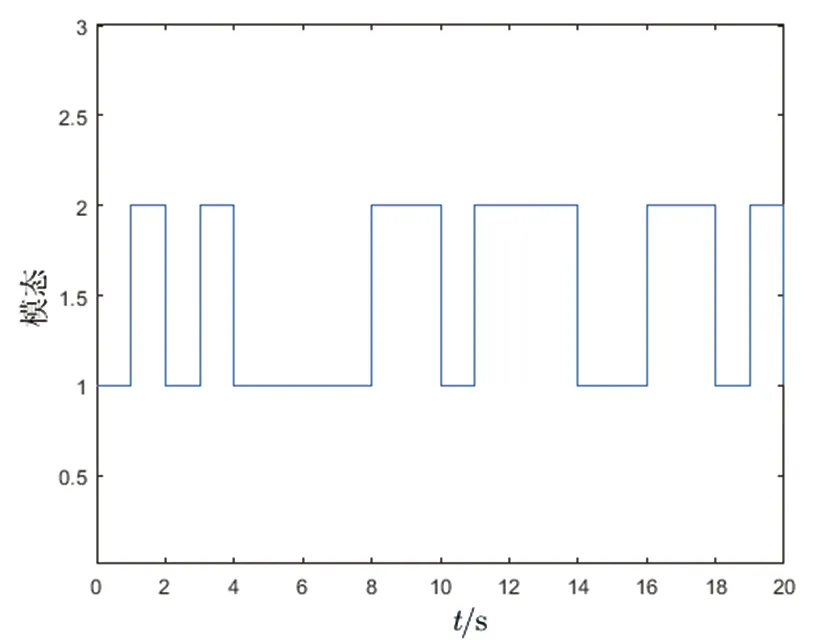
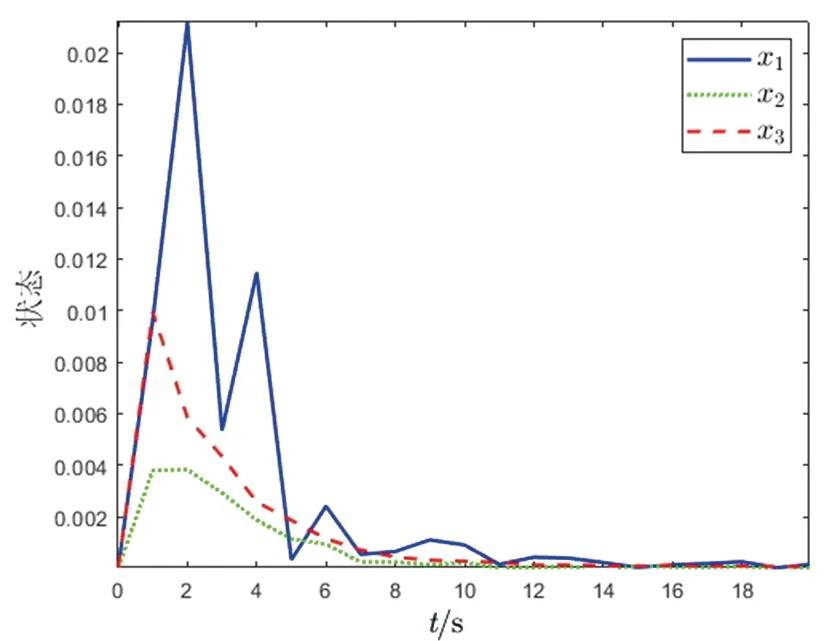
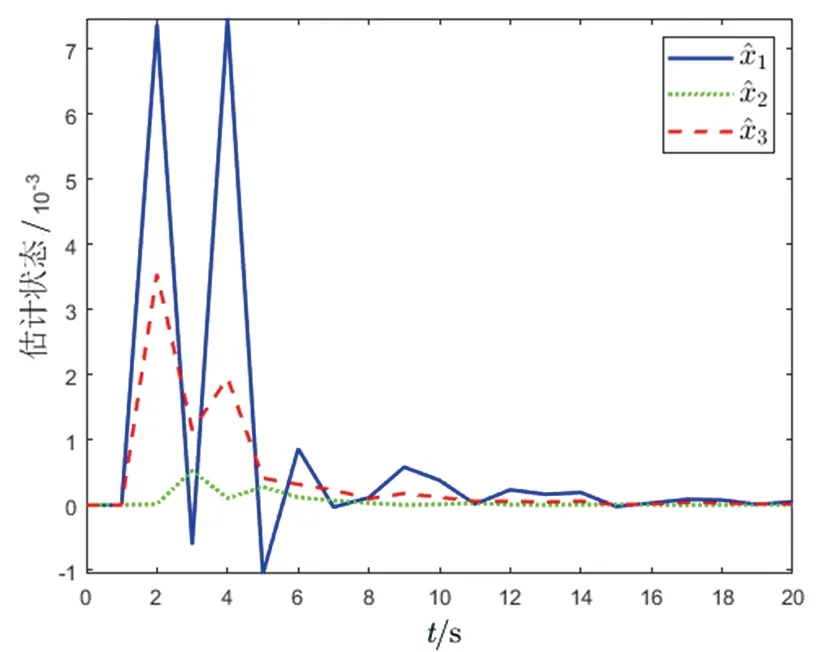
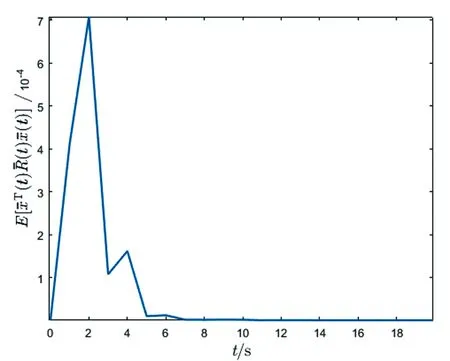
ηR-1(l) (31) ξ1R-1(l) (32) (33) (34) 因此,条件(29)和(30)能保证(14)成立。 (35) 注2当w(k)=0时,定理2退化为文献[44]的定理4;当w(k)=d=0时,定理2即为文献[43]的定理3。 注3条件(29)无法用线性矩阵不等式的方法求解,为了解决这个问题,将(29)转化为条件 (36) 式中λ是给定的足够小的常数。 根据引理1,条件(36)等价于下列线性矩阵不等式 (37) 注4条件(30)和(33)不是严格的线性矩阵不等式,但是,如果固定参数δ,上述条件就可以转化为基于线性矩阵不等式的可行性问题。因此,定理2中的可行性问题可以转化为下述具有固定参数δ的可行性问题: min(τ2+γ2) s.t. LMIs (30)—(33)和(37)。 注5基于上述讨论可知,当δ=1时,如果可以求得可行解,则可以证明本文所设计的有限时间H∞控制器可以保证时滞DMJSs有限时间有界和有限时间稳定。 本节将通过改进的害虫种群结构动态模型[46]证明本文所提方法的有效性。由于天敌数量、环境温度的突然变化,害虫种群的出生率、死亡率会发生改变,假设这些突然变化满足马尔可夫跳变规律;另一方面,害虫种群当前的数量受到过去数量的影响,将过去数量的影响描述为时滞。因此,改进的害虫种群结构动态模型可描述为形如(1)—(4)的系统,其中x1(k),x2(k),x3(k)分别表示在k时刻幼年害虫、未成熟害虫和成熟害虫的数量;u(k)表示人为对害虫种群数量的干预,如引进捕食者、喷洒杀虫剂等;v(k)表示从其他区域迁移至此区域的害虫的数量;z(k)表示该区域害虫的总数量;w(k)表示该区域的气温、降雨量等因素。 考虑具有两个模态的害虫种群结构动态模型,系数矩阵为 模态1: G(1)=1,G1(1)=0.06,G2(1)=0; 模态2: G(2)=1,G1(2)=0.05,G2(2)=0。 图1 τ和γ的局部最优界 图2 初始模态为1的系统(10)的切换信号 由定理2得τ=150.414 6,γ=105.952 6,反馈控制增益及观测器增益分别为: 图3 系统状态的响应 图4 估计状态的响应 图的演化 本文通过构造李雅普诺夫函数并结合线性矩阵不等式,设计了基于观测器的时滞离散时间马尔可夫跳变系统状态反馈控制器,给出了闭环误差系统有限时间有界并满足H∞性能指标的充分条件。此外,利用本文提出的设计方法可以研究离散时间模糊系统的有限时间H∞控制问题。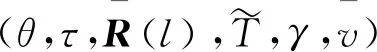


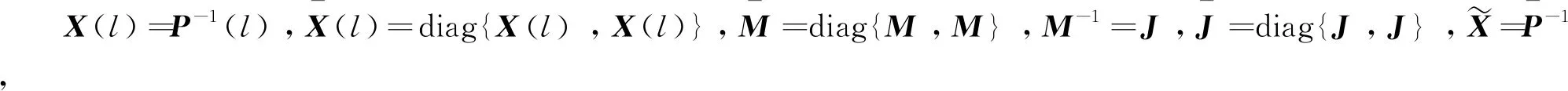
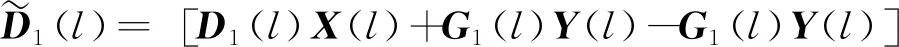
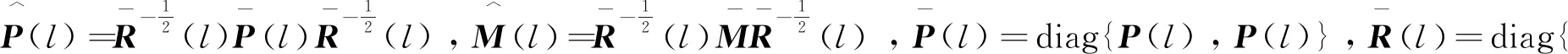

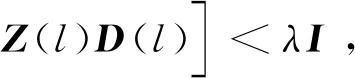
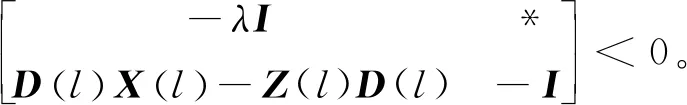
4 数值算例
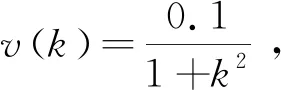

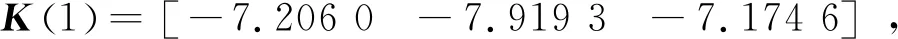

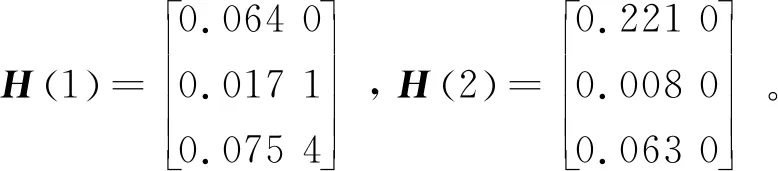
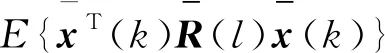
5 结束语
