十字滑环防自转机构间隙对涡旋啮合特性的影响

2022-04-27李冰，杨超，李超

流体机械 2022年3期

李冰，杨超，李超

（兰州理工大学石油化工学院，兰州 730050）

0 引言

涡旋式压缩机由于具有高效低噪等优良特性，被广泛应用于工程实际各领域。随着应用领域的拓宽，国内外学者对涡旋压缩机的相关研究也随之深入，涡旋压缩机的泄漏是影响压缩机性能的关键因素之一，目前，李力等[1]建立了涡旋压缩机针对径向间隙的泄漏数学模型，计算分析了压缩机热力过程和不同的径向间隙对压缩机泄漏的影响；杨骅等[2]全面的分析并比较了近几年来在涡旋压缩机泄漏方面模型的优缺点，提出了今后涡旋压缩机泄漏研究的方向；刘兴旺[3]分析了涡旋盘几何参数间的相互关系，提出了几何参数影响摩擦损失功率和泄漏损失功率；李超等[4]针对回转半径固定式曲轴结构的涡旋压缩机进行研究，得出了存在较大的自转角时，涡旋齿长时间运转容易疲劳断裂的结论；强建国[5]通过通用型线理论，用有限元模拟研究分析了涡旋齿的作用载荷、应力和变形的基本规律；宋红滚[6]归纳了涡旋压缩机的研究概况，分析几何公差等方面的国内外研究现状，对涡旋压缩机的装配特点和影响装配的关键几何公差进行了重点分析；刘红燕等[7-8]分析并找出了机构误差对切向泄漏间隙、泄漏量及泄漏率的影响。

这些已有的研究对提高压缩机性能和指导工程设计起到了积极推动作用。然而，由于实际加工制造和装配等因素，涡旋压缩机防自转机构间隙的客观存在，使得动涡旋产生自转运动，引起了动静涡旋径向啮合间隙发生改变。径向间隙变大会增加泄漏损失，而径向间隙减小会产生摩擦，导致涡旋齿侧壁面间应力增大。这严重影响了整个系统的稳定运行和使用寿命，因此，本文对十字滑环防自转机构配合间隙对涡旋压缩机系统稳定性影响进行了分析研究，确定了该间隙可允许的最大范围，可为涡旋压缩机的设计提供理论参考。

1 动静涡旋径向间隙数学模型

1.1 单一型线理论基础

涡旋压缩机的型线种类有很多种，但在工程实践中应用最为广泛的涡旋型线是圆渐开线。以渐开线展角φ作为参变量，圆的渐开线型线方程在直角坐标系下可表示为[9]：

1.2 静涡旋盘内外侧型线方程

涡旋齿内外侧型线的起始点发生线与x轴形成2个大小为α的夹角，结合公式的推导过程可知静涡旋齿内外侧壁面型线参数方程为：

1.3 正常工作时动涡旋盘的型线方程

动涡旋盘是由静涡旋盘旋转180°且相对偏置一定距离得到的（偏置距离为主轴偏心距Ror），则：

动涡旋盘基圆中心的坐标值（m，n）分别为：

正常工作时，动涡旋盘的内外壁面型线方程为：

式中 2——下标，动盘；

i，o——下标，涡旋齿内侧和外侧型线。

1.4 动涡旋盘发生自转后型线方程

当坐标顺时针旋转时相当于坐标系逆时针旋转。参见图1，以动涡旋盘基圆中心O2建立的直角坐标系X'O'Y'，通过顺时针旋转角度θ'得到直角坐标系X"O"Y"。设坐标平面上任意点C，在X'O'Y'坐标系下的坐标为（x'，y'），在 X"O"Y"坐标系下的坐标为（x"，y"）。

图1 坐标系逆时针旋转Fig.1 Counterclockwise rotation of the coordinate system

经分析可知，处于2个坐标系下的坐标具有下列关系：

代入静涡旋齿内外侧壁面方程，可得到动涡旋盘发生自转时的内外壁面型线方程为：

其中，动涡旋盘发生自转时的外壁面型线方程可知展开角与自转角的关系式：

式中 a——基圆半径；

φ——渐开线展角；

α——渐开线发生角。

1.5 自转角与啮合位置的变化关系

如图2所示，已知O1A1与x轴的夹角为φ1，O2A2与x轴的夹角为φ2，O2B1与 x'轴的夹角为，O2B2与x'轴的夹角为，则点C，D，E在静涡旋盘内侧渐开线上，即φ＝φC、φ2＝φD且φ1＝φE。点 C'，D'，E'在正常工作的动涡旋盘内侧渐开线上，即点C"，D"，E"在动涡旋盘发生自转后的外侧渐开线上，即

图2 涡旋齿自转运动示意Fig.2 Schematic diagram of rotary motion of the scroll tooth

假设动盘发生顺时针自转θ'后，动盘上任意一点E'到达啮合点C"位置的同时，原啮合位置处的点C'到达点D"位置。判断动盘自转的变化规律，就是确定点C"与点C的位置关系。

据坐标系逆时针旋转方程可知E'与C"的关系：

根据RtΔO1A1E'与RtΔO1AE"全等，可知A1E'＝AC"，同理 AC'＝A2D"。

因为E'和C'都在正常工作时的动涡旋盘外侧渐开线上，则φE＞φC。根据几何关系可知切线A1E'＞AC'，且AC"与AC在同一条直线上，即此时自转后啮合位置仍处于平行于动静涡旋盘中O1，O2连线的切线AC上，但间隙缩小。

所以AC'＝AC"，即点C"与点C重合，可推出假设成立，则动涡旋盘顺时针自转θ'后点E'到达啮合点C。

1.6 不同展开角对应的最大自转角θ'

当时θ'＝θ'max，静涡旋盘内侧渐开线与发生自转时的动涡旋盘外侧渐开线刚好卡死（即啮合），此时这2条渐开线有且仅有一个啮合点C，则点C的坐标存在以下关系：

通过Matlab运算可知，该隐式方程有2个不同解，根据实际情况，选取最小的解为可允许的最大自转角，其中，顺时针为负，逆时针为正。

1.7 径向间隙变化量的确定

由于防自转机构的干涉，导致自转后啮合点位置不能彻底到达点C，即同处在切线AC上，但C"与C无法重合。

则径向间隙的变化量可以通过联立以下公式求出：

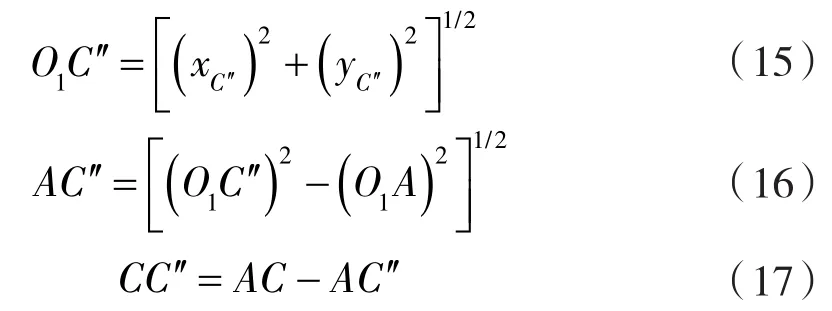
则自转后的最小啮合间隙：

最小间隙变化量为：

2 滑环间隙与径向间隙的关系

2.1 十字环与动涡旋盘的结构和运动关系

如图3所示，将静坐标XO1Y选在支架体上，其坐标原点与电机转子中心重合。因为动涡旋盘的十字滑环槽与十字环凸键A，B相连，所以十字环的中心与动涡旋盘在Y方向的运动保持同步，且只能在Y方向上进行往复运动。

图3 动静盘与十字环相对运动Fig.3 Schematic diagram of relative motion between orbiting and stationary scroll discs and the Oldham ring

2.2 十字滑环允许的最大自转角

Om到十字环的距离可以算为：

Om到O2的距离为：

因为滑槽和十字环间隙很小，则可近似看作：

2.3 滑槽间隙与径向间隙的关系

结合实际，十字滑环防自转机构能够有效防止涡旋压缩机产生自转，可知十字滑环间隙产生的最大自转角不能大于涡旋齿可允许的最大自转角，即的取值范围为。则十字滑环槽的间隙最终确定了径向间隙的变化量。

2.4 自转后的压缩腔容积变化

如图4所示，设压缩腔顺序编号由里到外分别为第一压缩腔、第二压缩腔以及第三压缩腔。

图4 某啮合时刻所形成的压缩腔室示意Fig.4 Schematic diagram of the compression chamber formed at a certain meshing time

3 Matlab实例计算

已知基圆半径为 a＝3.5 mm，回转半径 Ror＝6.49 mm，渐开线发生角α＝0.643 rad，十字滑环内外径分别为120，142 mm。通过动盘基圆中心O2的位置判断m和n的正负符号。

设定主轴转角为0时吸气结束开始压缩，根据上述推导的公式进行迭代运算，可知3个压缩腔变化趋势相似，所允许的最大自转角随着主轴转角的变大而缩小。

由于第三压缩腔渐开线发生线长度最大，即在相同的自转角度下，第三压缩腔转动的弧度最长自转的距离最大，所以需确定第三压缩腔渐开线展角与其对应的最大自转角。

如图5所示，第三压缩腔中啮合点C可允许的最大自转角θ'max求解出了2个值，正负值表示自转的方向。

图5 第三压缩腔最大自转角变化规律Fig.5 Variation law of maximum rotation angle of the third compression chamber

依据实际要求，本文寻找的是动静涡旋盘可允许转动的最小值，则图中求解值2即为动涡旋可允许的最大自转角θ'max随曲轴转角的变化规律。

主轴旋转280°时的最大自转范围如图6所示。从图5中可以看出，当主轴转角大于280°时开始反方向旋转，则可推出动静涡旋齿在主轴转角到达280°左右时，可允许的自转弧度最小。所以，动涡旋齿可允许的最大自转角的弧度为-0.000 51，即当主轴顺时针旋转280°时，可允许的最大自转角最小为0.029 2°，则是十字环凸键与动涡旋盘背面滑环槽间隙所造成的自转角应处于[0，0.029 2°）。