音波管长度对射流振荡器性能的影响
2022-04-27吾特库尔努尔买买提刘学武张瑞丹闫朋泽胡大鹏
吾特库尔·努尔买买提,刘学武,张瑞丹,闫朋泽,胡大鹏
(大连理工大学 化工学院,辽宁大连 116024)
符号说明:
d——音波管宽度,mm;
f——射流振荡频率,Hz;
h——劈距,mm;
K——射流振荡器总压保持率;
L——音波管长度,mm;
l——直段长,mm;
m——射流振荡器出口质量流率,g/ms;
mi—— 一周期内射流振荡器入口射流质量,g;
mr—— 一周期内射流振荡器出口回流质量,g;
Pe——射流振荡器激励口处总压,MPa;
Pi——射流振荡器入口总压,MPa;
PO——射流振荡器分支出口总压时均值,MPa;
POS——射流振荡器出口静压,MPa;
R——射流附壁切换周期占比(射流切换时间与振荡周期的比值);
s——位差,mm;
T——射流振荡周期,ms;
w——喷嘴宽度,mm;
α——一周期内射流振荡器出口回流率(射流振荡器出口回流质量与入口射流质量的比值);
ΔP——两激励口的质量加权平均总压的差值,MPa;
ε——射流膨胀比(射流振荡器入口总压与出口静压的比值);
θ——出口流道张角,(°);
ρk——出口截面第k个网格处的气体密度;
vk——当地气速;
Ak——第k个网格面积;
ptk——分支出口截面第k个网格外边界节点总压。
0 引言
基于 Coanda效应[1]的流体振荡器[2-4]能将稳定射流转化为脉冲射流,且因其设计简单,耐用而被广泛应用于流量控制[5]、切割[6-7]、流动分离控制[8-9]、石油钻井[10-11]等方面。自激励射流振荡器[12-13]是利用元件内部特殊的结构实现稳定的脉动射流,音波式射流振荡器[14-15]就是其中之一,主射流在激励口产生的扰动作用下,交替从2个出口流出,产生稳定的脉动射流,可用于静止式气波制冷机[16-17]的气体分布。TESAR[18]提出了一种无运动部件的混合合成喷射致动器,可通过调节音波管的长度来调节射流振荡频率;胡大鹏等[19]通过实验与数值模拟相结合的方法研究了几何尺寸对音波式射流振荡器射流流动特征的影响,发现音波管长度、劈距及位差均存在使射流稳定振荡的范围,且几何尺寸之间存在耦合关系;FEIKEMA等[20]通过数值计算及实验对射流振荡器进行了研究,发现2个激励口的动量通量比的平方根是诱导射流切换的一个重要参数;陈祖志等[21]发现音波式射流振荡器几何因素对射流总压损失均有影响,振荡腔几何尺寸存在最优值;之后,李俊龙[22]结合能效指标对音波式射流振荡器进行了几何优化。
目前,音波式射流振荡器的研究多集中于几何结构与内部流场特性和振荡性能的关联,而对几何及操作参数与能效指标关联的研究相对缺乏。实际应用过程中发现,射流振荡器应用于气波制冷机气体分配时,回流现象的存在会将气波管内已制冷的气体直接倒吸进射流振荡器内,排气口排出的冷气量减少,导致气波制冷机制冷效率降低[23]。
本文在几何尺寸优化后的音波式射流振荡器的基础上,通过CFD模拟研究不同操作参数及音波管长度对射流振荡器的性能指标及回流特性的影响进行分析,为音波式射流振荡器的实际应用提供理论及模拟支持。
1 CFD数值模拟
1.1 计算模型及性能指标
音波式射流振荡器的几何结构如图1(a)所示,其中音波管长度L为上激励口逆时针到下激励口的距离。计算模型的ICEM(Integrated Computer Engineering and Manufacturing code)结构化网格划分如图1(b)所示,独立性分析确定网格最大尺寸0.2 mm,将喷嘴附近网格加密,沿流动方向渐疏。
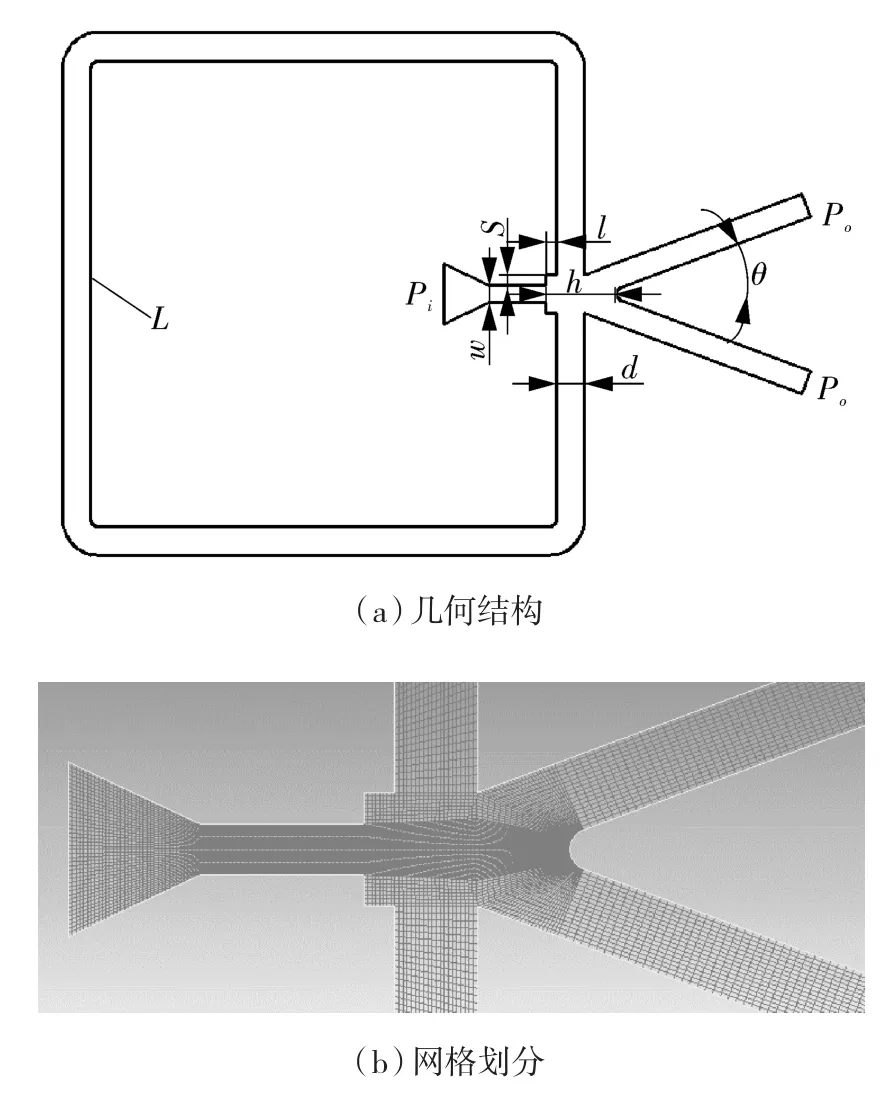
图1 音波式射流振荡器几何结构及网格划分Fig.1 Geometric structure and mesh division of sound wave jet oscillator
在以往的研究中[21],仅用振荡指标及能效指标衡量振荡器的性能。振荡指标指的是射流振荡器是否容易实现稳定振荡,用射流振荡频率f及射流附壁切换周期占比R(射流切换时间与振荡周期的比值)衡量;能效指标用振荡器分支出口流道总压时均值Pout,与振荡器入口总压Pi的比值 K 来衡量,称为总压保持率[22],K 越接近 1,损失越小。
由于总压包括气流的静压和动压,所以分支出口流道时均总压与气体质量相关。Pout的求算过程为:射流稳定附壁时,分支流道出口各个Δt时段,对出口各网格流出质量流量与网格节点总压的乘积积分,再除以该时间段内总的质量流量,即:
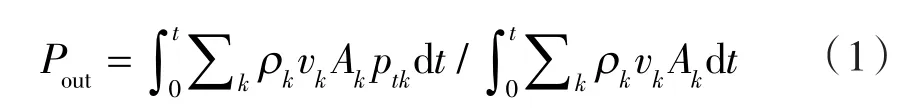
射流振荡器存在回流现象(图2中出口流道),故定义回流比α衡量射流振荡器回流特性,其计算式为:


图2 射流振荡器某一时刻流体迹线Fig.2 Fluid trace diagram of jet oscillator at a certain moment
1.2 数值模拟方法
模拟了不同音波管长度下,音波式射流振荡器的性能。为兼顾普遍性,将其余几何参数优化后的音波式射流振荡器作为研究对象,其尺寸为:喷嘴出口宽w=2.5 mm,劈距h=10 mm,位差s=1.5 mm,直段长 l=1.5 mm,音波管宽度 d=4 mm,出口流道张角θ=20°。射流振荡器入口为压力入口;出口为压力出口;其余均为固壁边界条件;介质为理想气体。
射流振荡器内流体为超音速,可压缩强湍流流动,可采用求解时均Navier-Stokes方程的Reynolds平均法。由于喷嘴射流湍流的各向异性,采用两方程Realizable k-ε湍流模型,以有限体积法对控制方程进行离散。扩散项选取计算效率高、二阶精度的中心差分格式,收敛较快。对流项为各向异性,为避免数值振荡,采用迎风格式中的Roe通量差分分裂的MUSCL格式进行离散,以二阶全隐式时间步进行迭代。
2 模拟结果及分析
本文模拟了 Pi=0.36 MPa、POS=0.18 MPa、流量为 2.55 kg/s;Pi=0.36 MPa、POS=0.12 MPa、流量为2.89 kg/s及 Pi=0.24 MPa、POS=0.12 MPa,流量为1.86 kg/s即入口总压一定(0.36 MPa)不同膨胀比(ε=2和3)及相同膨胀比(ε=2),不同操作压力水平(Pi=0.36 MPa 和 Pi=0.24 MPa)时,音波管长度对射流振荡器振荡性能、能效指标及其回流特性的影响。
2.1 音波式射流振荡器内流场分布
图3示出音波管长度318 mm时,1个周期内射流振荡器内各关键时刻总压云图。

图3 射流不同状态时射流振荡器内总压云图Fig.3 The total pressure nephogram in the jet oscillator when the jet is in different states
射流经喷嘴射入振荡器,在Coanda效应作用下,射流附于一侧壁面,从一个出口流出;同时,音波管内产生相应压缩波及膨胀波,传至音波管另一侧,射流在此扰动下进行附壁切换。
正是音波管两激励口处压差的存在,才能维持射流的稳定附壁及切换。图4示出射流振荡器入口总压Pi、一出口处的总压Po(上出口流道)、激励口(下激励口)总压Pe及两激励口总压压差ΔP随时间的分布。Pe变化趋势与Po保持一致,且呈周期性变化,当Pe值增大到一定值时,即ΔP≥0(下激励口总压≥上激励口总压)时,射流开始切换到上出口壁面,当ΔP达到最大值时,出口处射流的总压也达到最大值,这时射流稳定地附于上壁面。

图4 射流振荡器Pi,Po,Pe及ΔP随时间的变化Fig.4 Variation of Pi,Po,Peand ΔP of jet oscillator with time
图5示出不同时刻音波管内沿程总压分布,将上激励口取作音波管长度的起点,沿逆时针分别为 1/4L,1/2L,3/4L,下激励口为 L。t1~t2时刻对应射流由下出口流道内侧壁面到下出口流道外侧壁面转换,直到t3时刻,射流稳定地附于下壁面外侧,t4~t5时刻对应射流由下附壁面逐渐向上壁面切换,t6时刻射流处于分流劈处,此时音波管内的压力分布相对均匀,两激励口的压差最小,t7时刻为射流稳定附于上壁面,其形态与t3时刻时相同,只是变化趋势相反。
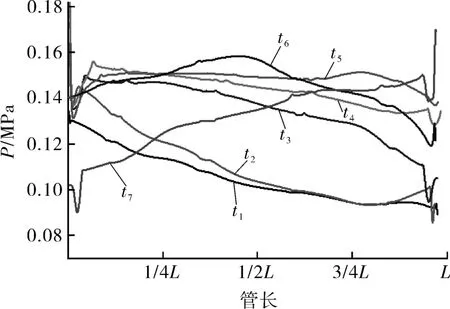
图5 不同时刻音波管内总压沿管长分布Fig.5 Distribution of total pressure along the length of the tube at different moments
从不同时刻音波管内总压随时间的变化可看出,当射流稳定附于下壁面时,由于上激励口处的流体压力较大,在该处产生一道激波并沿音波管传递至下激励口,同时,由于下激励口压力较低,产生一道膨胀波沿音波管传递至上激励口,此行为引起两激励口压差ΔP符号变化,使射流开始切换。
2.2 音波管长度对射流振荡器振荡性能的影响
音波管内激波与膨胀波传播引起射流稳定振荡,因此,音波管长度对射流振荡器是重要的几何参数之一。模拟了L=148~318 mm音波式射流振荡器在不同膨胀比及操作压力时射流振荡器的性能的变化。
图6示出不同膨胀比及操作压力下,射流振荡频率f随音波管长度L的变化。由图可看出,f均呈现与音波管长度成反比的变化趋势,且大膨胀比ε时,f随音波管长度的变化斜率大于小膨胀比时的斜率。

图6 射流振荡频率f 随音波管长度L的变化Fig.6 Variation of jet oscillation frequency f with the length L of the sound wave tube
当L相同时,ε为3时射流振荡频率最大,当L=158 mm时达到频率466 Hz,大操作压力下ε为2次之,此时f最大能达到391 Hz,小操作压力下ε为2时f值最小,f最大值为371 Hz。这是由于当ε较大时,激励口处产生的激波及膨胀波强度相对较大,能在音波管内高速传播,且到达另一侧激励口时,激波及膨胀波的衰减很小,能够强有力的推动射流切换。
当L小到一定程度时,f的值不会再大幅度增加,且在模拟中发现,当ε为3,L为148 mm时,射流在两出口之间振荡的同时,在同一出口流道中会剧烈摆动,导致出口总压不稳定。这是由于当膨胀比较大,L较小时,音波管内波强度较高,传递至另外一侧激励口时,引起剧烈扰动,导致主射流的稳定性降低。由此可以看出,音波管长度不是越短越易获得稳定的高频脉动射流。
图7示出射流附壁切换周期占比R随音波管长度L的变化,随着L的增大,R均呈现下降趋势,且斜率逐渐减小,这是由于随着L的增加,射流振荡周期逐渐变长,射流切换时间占比减小。
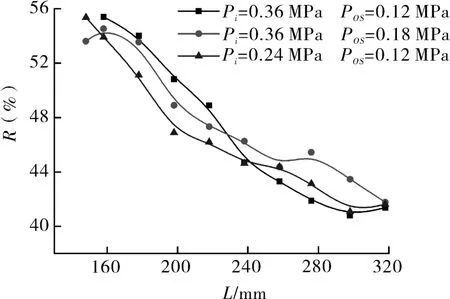
图7 射流附壁切换周期占比R随音波管长度L的变化Fig.7 The variation of the ratio of the attachment switching period R of the jet with the length of the sound wave tube L
2.3 音波管长度对射流振荡器能效指标的影响
图8示出不同膨胀比及操作压力下,射流总压保持率K随管长的变化。L相同时,小膨胀比、小操作压力下K值最大,小膨胀比、大操作压力次之,大膨胀比时K值最小。以L=158 mm时为例,K值从大到小依次为74.89%,73.83%和62.30%。由此可知,膨胀比对K的影响较操作压力大,膨胀比越大,K值越小。
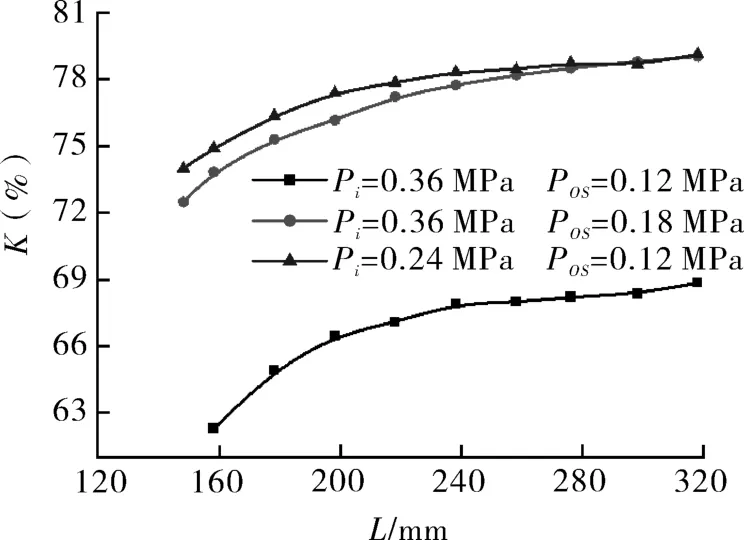
图8 射流总压保持率K随音波管长度L的变化Fig.8 The variation of the total pressure retention rate K of the jet with the length L of the sound wave tube
Pi为0.36 MPa,膨胀比ε分别为2和3时,随着音波管长度的变化,K均呈现逐渐增加的趋势,且增加趋势逐渐减缓,在L=318 mm处达到最大值79.01%(ε=2)和68.84%(ε=3)。当L由158 mm增加到318 mm,K值都增加了6%左右。膨胀比ε为2时,不同操作压力下,K随L的增长幅度基本一致,在L为298和318 mm时K值相同。
取射流稳定附壁时即上文在计算PO所选取的T/2时间内,两激励口的质量加权平均总压的差值为ΔP,图9示出ΔP/Pi随L的变化,不同操作压力及膨胀比时,ΔP均随L的增大而增大,与K值具有相同的变化趋势。L相同时,大膨胀比时ΔP/Pi的值最大,小膨胀比、小操作压力次之,小膨胀比、大操作压力最小。膨胀比较操作压力而言对ΔP/Pi的影响更大。这说明,当膨胀比较大时,在两激励口之间形成高强度的激波及膨胀波,使得两激励口处的压差更大,射流切换更加迅速,这在图7有所体现:L>238 mm时,大膨胀比下ΔP/Pi随L的增大急剧增大,而此时大膨胀比时的R值急剧减小。
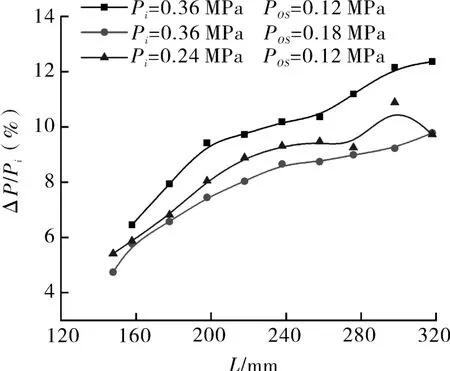
图9 射流振荡器两激励口ΔP/Pi随音波管长度L的变化Fig.9 Variation of ΔP/Piat the two excitation ports of the jet
从图8,9中分析,膨胀比相同时,射流振荡器的K值与ΔP/Pi有明显的关联性,ΔP/Pi越大,即激励口相对压差越大,其推动力越大,射流中间转换耗能越少,K值越大;而大膨胀比时,射流从喷嘴喷出时,速度激增,撞击到分流劈时,所消耗的能量大于小膨胀比时的耗能,再加上沿程的摩擦损失,使得最终出口处的总压保持率K下降。
2.4 音波管长度对振荡器回流特性的影响
图10示出振荡器一出口质量流率m随时间的变化,正值部分为流体从出口流出,负值部分为流体经出口回流至振荡器内。
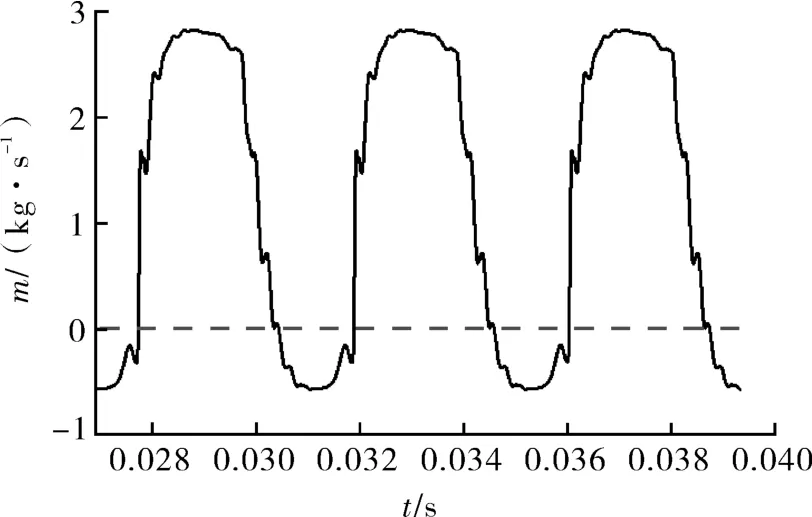
图10 射流振荡器出口质量流率m随时间的变化Fig.10 The variation of the mass flow rate m of the jet oscillator outlet with time
图11示出回流率α在不同膨胀比、及不同操作压力时随音波管长度L的变化,α随L的增大均呈现逐渐增大的趋势,其中ε=2时增长斜率逐渐降低,ε=3时增长斜率在不断增高。α随L的增大而增大是因为随着L的增加,进入音波管的气体流量逐渐增多,进入振荡腔的气体量减少,腔体内的静压越低,需要从外界卷吸更多的气体来维持压力平衡。在模拟的L的范围内,α的增长有所不同,小膨胀比小操作压力时α从1.99%增长到5.03%,小膨胀比,大操作压力时α从1.2%增长到4.95%,大膨胀比时α从1.63%增长到4.30%。
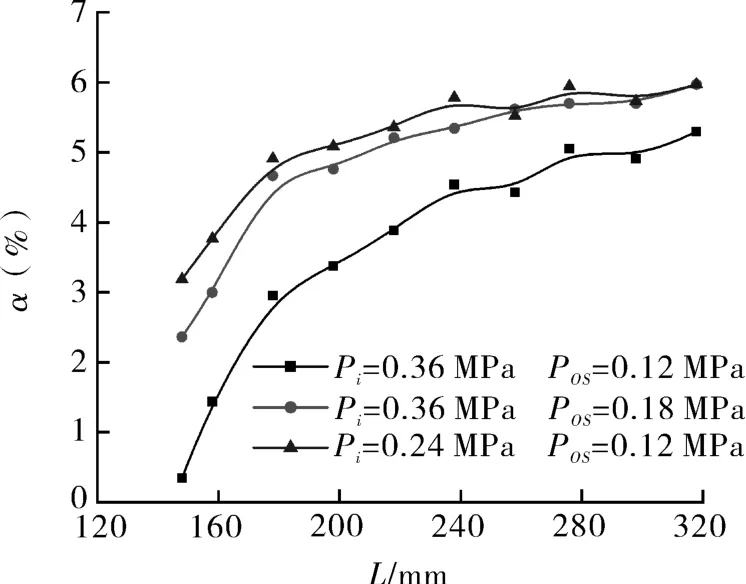
图11 射流振荡器出口回流率α随音波管长度L的变化Fig.11 Variation of the reflux rate α of the jet oscillator with the length L of the sound wave tube
对比3种操作情况,可发现小膨胀比、小操作压力时振荡器的回流率最高,小膨胀比、大操作压力次之,大膨胀比时的回流率最小。以L=238 mm为例,3个值由大到小分别为4.86%,4.55%和4.10%。
3 结论
(1)射流振荡频率f及射流切换周期占比R均与音波管长度成反比,膨胀比较大和操作压力较大时,振荡频率较大;当L小到一定程度时,f的值不会再大幅度增加,且会导致射流不稳定振荡。
(2)随着音波管长度L的增加,K均呈现逐渐增加的趋势,且增加趋势逐渐减缓;L相同时,膨胀比小、操作压力小时K值较大;膨胀比相同时,射流振荡器的K值与ΔP/Pi有明显的关联性,ΔP/Pi越大,K值越大;而大膨胀比时,K的大小还与射流的沿程损失有关。
(3)回流率α随音波管长度L的增大呈现逐渐增大的趋势,其中膨胀比ε=2时增长斜率逐渐降低,膨胀比ε=3时增长斜率在不断增高;3种压力条件下,小膨胀比、低压力水平时的回流率最高,小膨胀比、高压力水平次之,大膨胀比时的回流率最小。
(4)射流振荡器出口支路气体回流是维持控制口压差的主要原因之一,2个控制口ΔP/Pi的值又影响着射流的总压保持率和附壁切换周期占比。回流率相同时,大膨胀比时两控制口ΔP/Pi最大;相同的ΔP/Pi小膨胀比时,更易获得附壁切换周期小、总压保持率高的振荡射流。
