基于试验设计-遗传算法的开关电磁阀响应特性优化*

李红 谢鼎盛 张泽涵 储江伟

（东北林业大学，哈尔滨 150040）

主题词：开关电磁阀 动态响应特性 试验设计 遗传算法

1 前言

机械直连的液压制动系统已无法满足汽车电动化、智能化的发展要求。线控制动系统的制动踏板不直接通过液压回路与车轮制动分泵相连，能够实现再生制动能量回收。作为线控制动系统的关键部件，开关电磁阀的性能直接影响汽车的制动效能。文献[3]利用新型材料设计了一种菱形位移放大结构式驱动器，可有效控制电磁阀开启及关闭时间。文献[4]、文献[5]研究了控制电路在不同驱动策略下开关电磁阀的流量响应特性，多路混合驱动、复合脉冲宽度调制（Pulse Width Modulation，PWM）控制策略可以改善电磁阀开关响应特性，但高频驱动电压使线圈温度场发生变化，导致内阻波动。文献[2]、文献[6]利用电流精确控制电磁阀开度，实现电磁阀流量非线性的可控性，但小电流驱动状态下，阀口流量波动较大。针对高速开关阀流量控制存在的死区和饱和区，文献[7]利用脉宽调制和脉频调制方式实现流量的线性化。文献[8]、文献[9]分别利用粒子群优化算法和智能PWM控制算法实现了电磁阀的快速开关特性及电磁线圈的低能耗要求。

上述文献几乎都是从新型材料驱动器或智能驱动策略角度改善电磁阀的动态响应特性，本文结合设计经验建模，从试验设计角度研究电磁阀动态特性，以某车型适配的一款常开电磁阀为研究对象，建立其AMESim模型，并利用开关电磁阀响应测试台验证所建模型的有效性，基于建立的AMESim 模型，明确电磁阀阀芯动作机理，利用控制变量法分析弹簧刚度、线圈电阻及阀芯总质量对流量特性的影响，提出一种基于试验设计-遗传算法的优化方法，有利于改善电磁阀动态响应特性。

2 计算模型建立

2.1 高速开关电磁阀模型

高速开关电磁阀由阀芯、阀座、动铁、静铁、回位弹簧、隔磁管、密封圈等零件组成，是线控液压系统中工作特性最复杂的元件，如图1所示。常开式电磁阀通电时，阀芯及动铁在弹簧力、液压力、电磁力和摩擦力作用下下移，进、出油口关闭；断电时，阀芯及动铁在弹簧力及摩擦力作用下上移，进、出油口连通。常闭式电磁阀工作原理类似，其区别是通电时电磁阀打开。

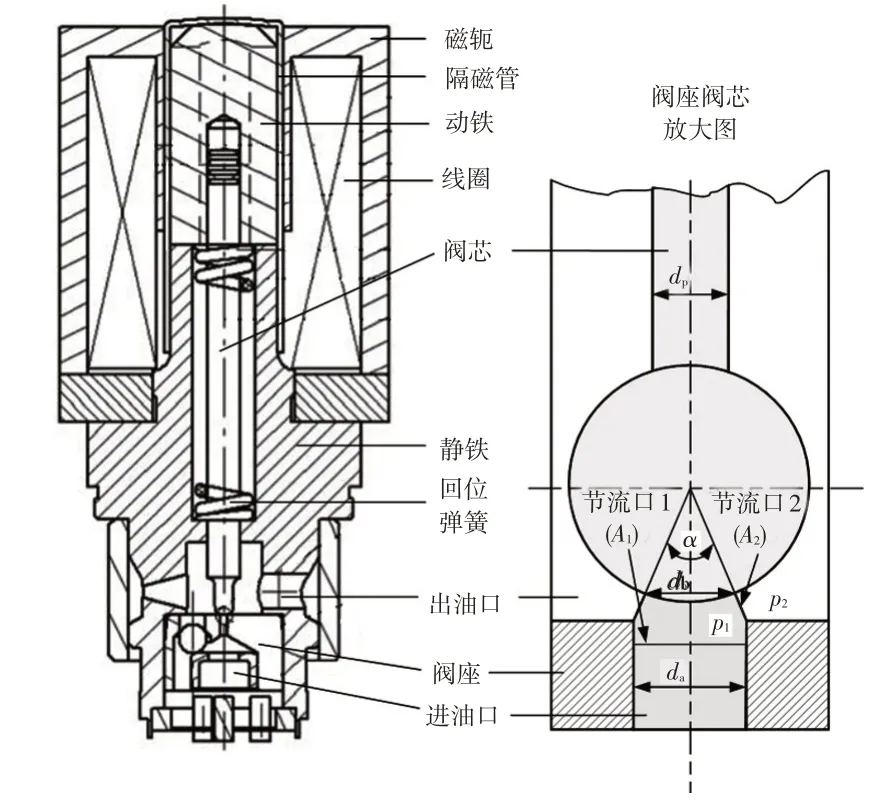
图1 开关电磁阀结构

2.1.1 电磁力

电磁阀线圈通入电流后产生电磁力，通过插值法实时计算电磁阀电磁力，利用有限元方法获得了电流-阀芯位移-电磁力的关系，如图2所示。

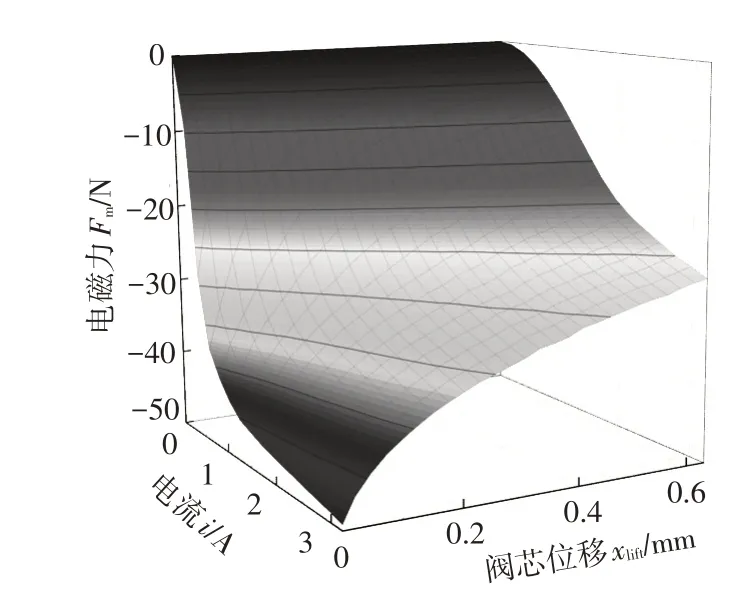
图2 电磁力-阀芯位移-电流关系

电磁阀线圈的电压求解公为：

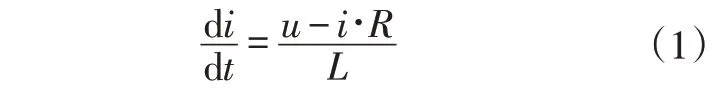
式中，为线圈电压；为线圈电阻；为线圈电感。

2.1.2 液体作用力

阀芯工作中受到的液体作用力包括液压力和冲击力，在其求解过程中以图1进油口中制动液为控制对象，其内、外的压力分别为、，液压力为：

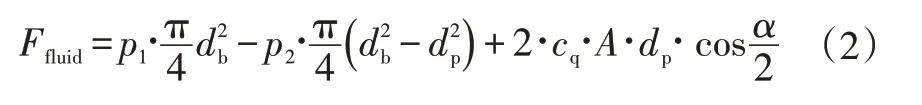
式中，为的有效作用面积直径；为阀杆直径；为流量系数；min{,}为过流面积；、为节流口1、2处的面积；为流向角。

2.2 动铁及阀芯的运动学方程

线圈不通电时，阀芯处于最大位移处。通电后，电磁阀阀芯及动铁在弹簧力、液体作用力、滑动摩擦力及电磁力作用下运动，运动学方程为：

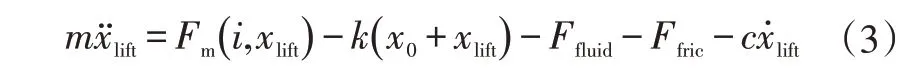
其中，摩擦力为：

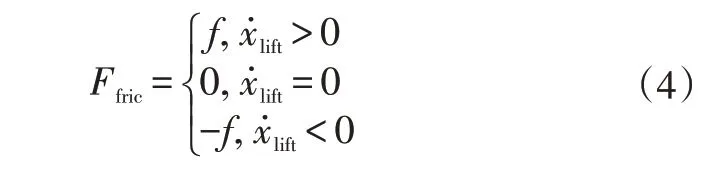
式中，为阀芯及动铁质量；为回位弹簧刚度；为弹簧预压缩量；为阀芯动摩擦力；为阻尼系数；为阀芯位移。

3 电磁阀AMESim模型验证

3.1 测试系统

鉴于AMESim 中所有的模型都经过了严格的测试和试验验证，本文基于AMESim软件建立了开关电磁阀的物理模型。以某车型适配的一款常开电磁阀为研究对象搭建了测试平台，验证所建物理模型的有效性。开关电磁阀响应特性测试台如图3 所示，由电磁阀阀体、轮缸、压力传感器、直流电源、传感器供电电源及上位机组成。

图3 开关电磁阀响应特性测试台

3.2 测试过程

利用直流电源控制电磁阀线圈通电电流，开关电磁阀响应特性测试流程如图4所示。

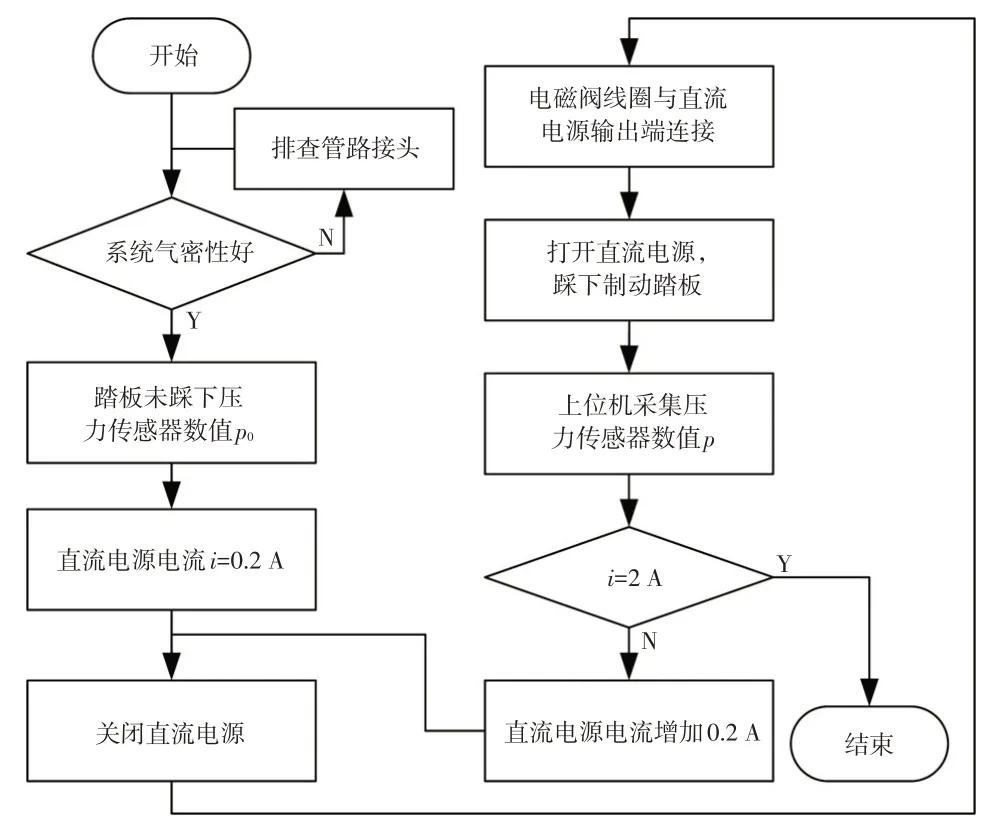
图4 测试流程

3.3 结果分析

试验过程中：直流电源电流设定为0.6 A时，踏板克服空行程后无法踩下，此时上位机采集的压力传感器读数为13 kPa；直流电源电流设定为0.4 A 时，踏板可踩下，此时压力传感器读数为335 kPa。上述数据表明，电磁阀线圈给定电流值在0.4～0.6 A范围内某一数值时电磁阀关闭。根据测试流程，重新设定直流电源电流初始值和增量分别为0.401 A、0.001 A，直到传感器压力约等于，该电流即为电磁阀关闭需求电流，表1 记录了直流电源电流设定值为0.591～0.598 A时压力传感器测量的电磁阀出口压力。

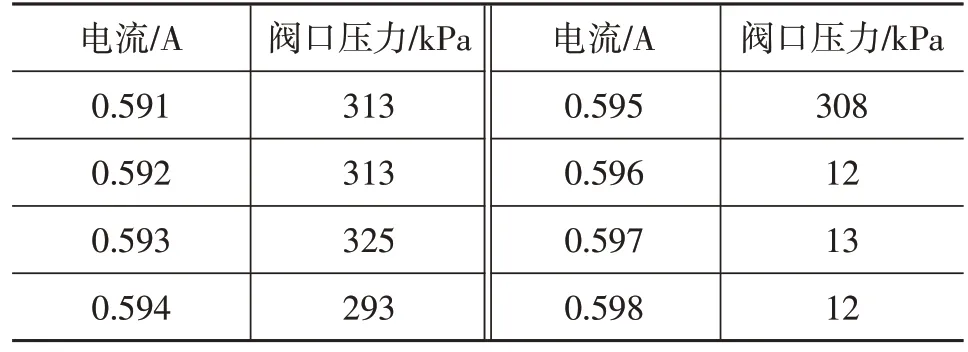
表1 开关电磁阀出口的压力

仿真模型中电磁阀的出油口直接与油箱相连，采集的是电磁阀出口流量，电磁阀线圈通电电流由0.595 A增大到0.596 A时，阀口流量由0.790 L/min 降低到0，此时电磁阀关闭。由表1 可知，线圈通入电流增大到0.596 A时，阀口压力降为12 kPa。上述数据表明，基于AMESim软件建立的常开电磁阀模型有效。

4 电磁阀流量特性分析

4.1 阀芯动作机理

以建立的常开式电磁阀AMESim模型为基础，分析电磁阀阀芯动作机理，电磁阀结构参数如表2所示。

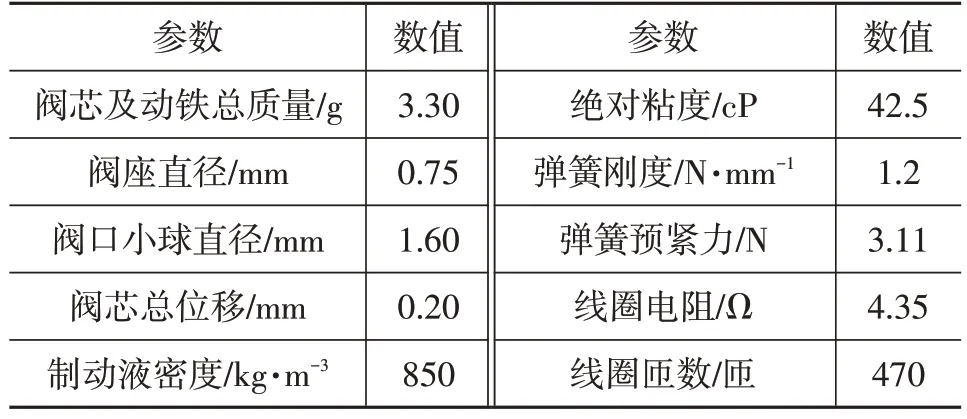
表2 开关电磁阀参数

为了研究电磁阀参数对出油口流量特性的影响，假设电磁阀进油口压力为1 MPa，控制电路给定周期为0.2 s 的PWM 信号，电磁阀阀口流量特性曲线如图5所示。

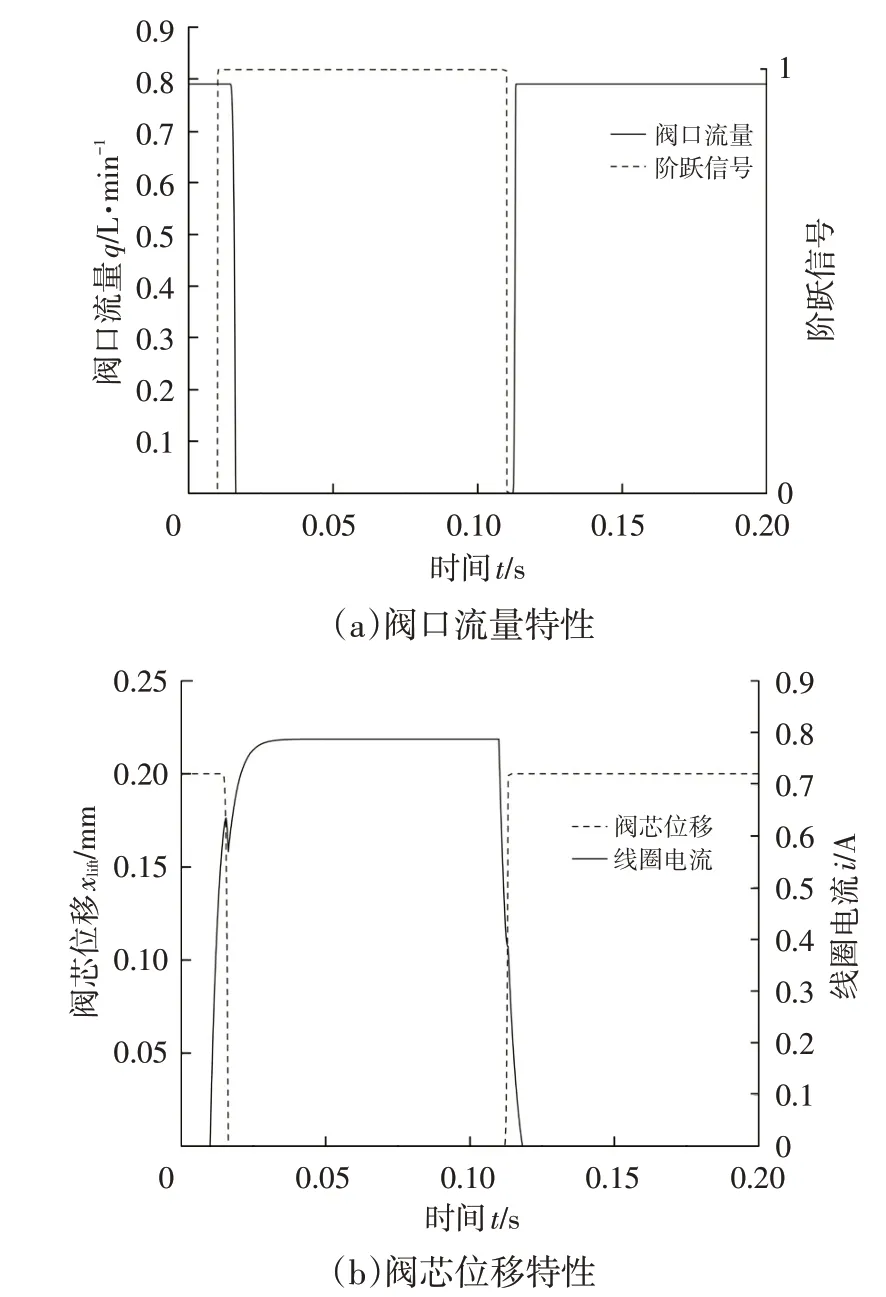
图5 开关电磁阀阀口特性曲线

第0～0.01 s范围内，控制电路信号给定值为0，阀芯处于最大位移处，阀口流量为0.79 L/min。第0.01～0.11 s范围内，电磁阀给定信号值为1：由于线圈电感的作用使得第0.01～0.014 4 s 内线圈电流逐渐增大，但此时电磁力不足以克服阻力使阀芯运动，阀芯仍处于最大位移0.20 mm 处，阀口流量无变化；第0.014 4～0.016 5 s 内阀芯位移由0.20 mm 减小至0，工作气隙的变化使线圈内产生反电动势，线圈电流减小，直到阀芯完全落座后反电动势降为0，随后线圈电流继续增加。第0.11～0.20 s时间段内，控制电路信号给定值为0，线圈内电流逐渐减小：第0.11～0.111 9 s内，阀芯受到的电磁力大于弹簧预紧力，阀口流量仍为0；第0.111 9～0.113 9 s 内，弹簧预紧力与电磁力合力推动阀芯远离阀座，当阀芯位移由0 增大到0.20 mm 时，电磁阀完全打开，阀口流量达到0.79 L/min。

4.2 结构参数对阀口流量的影响

忽略电磁阀运行环境差异的影响，由式（3）可知，电磁阀的弹簧特性、阀本体结构及电磁部分均会对阀口流量特性产生影响。本文提取弹簧刚度、阀芯动铁总质量及线圈电阻3个参数，利用控制变量法研究阀口的流量特性。控制变量法是在蒙特卡洛方法中用于减小方差的一种技术方法，可通过对已知量的了解减少对未知量估计的误差。本文采用单一变量控制法对不同弹簧刚度、阀芯动铁总质量及线圈电阻条件下阀口流量随时间变化的特性进行仿真。

设电磁阀进油口压力为1 MPa，阀芯动铁总质量为3.3 g，线圈电阻为6 Ω，当弹簧刚度分别为1 N/mm、4 N/mm、7 N/mm时，出油口流量随时间的变化特性如图6 所示。阀口流量分别在第20.7 ms、第21.2 ms 和第22.5 ms 由0.79 L/min 降为0，电磁阀吸合时间分别为10.6 ms、11.1 ms 和12.4 ms。随着弹簧刚度的增大，响应时间逐渐变长。

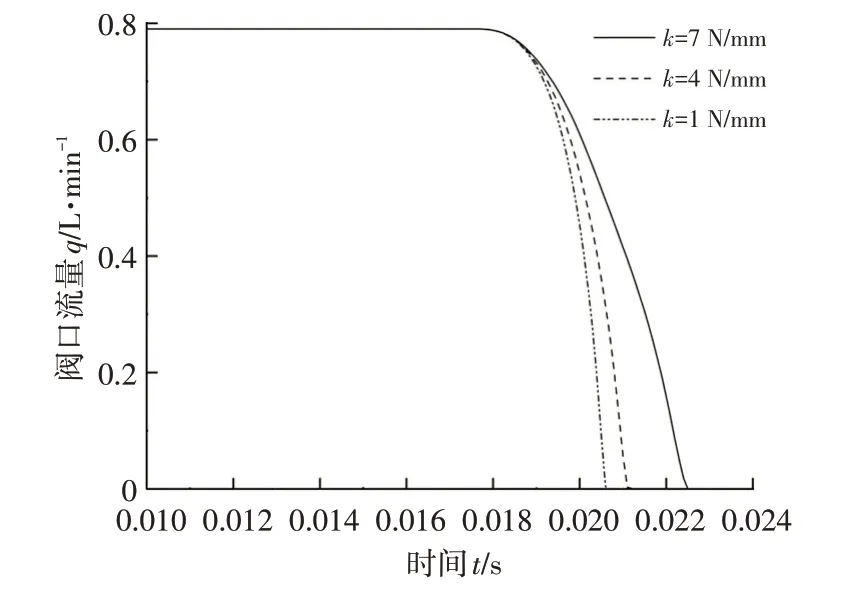
图6 弹簧刚度对阀口流量的影响

设电磁阀进油口压力为1 MPa，线圈电阻为6 Ω，弹簧刚度为1 N/mm，当阀芯动铁质量分别为3.3 g、6.3 g、9.3 g 时，出油口流量随时间的变化特性如图7 所示。阀口流量分别在第20.7 ms、第21.5 ms 和第22.1 s 由0.79 L/min 降为0，电磁阀吸合时间分别为10.6 ms、11.4 ms和12.0 ms。电磁阀吸合时间随阀芯动铁总质量的增大而延长。

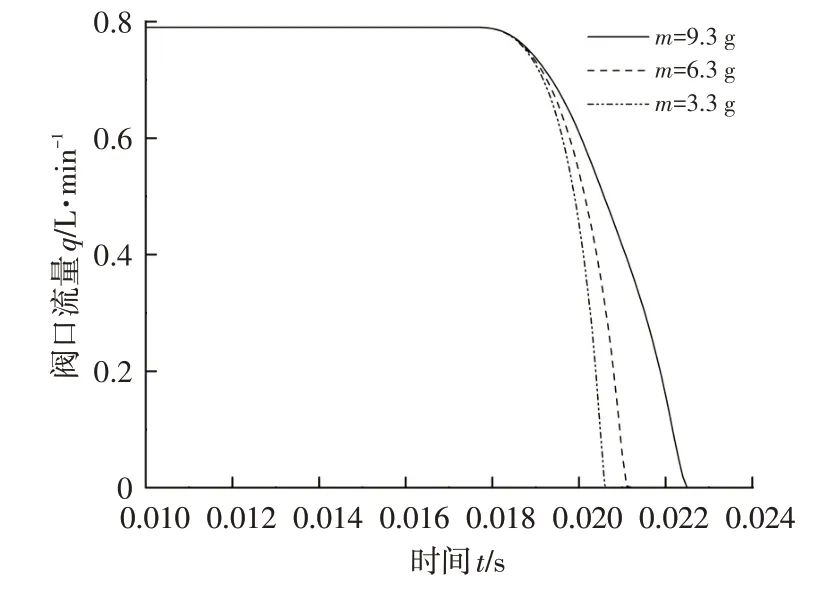
图7 阀芯质量对阀口流量的影响

设电磁阀进油口压力为1 MPa，阀芯动铁总质量为3.3 g，弹簧刚度为1 N/mm，当线圈电阻分别为4 Ω、5 Ω、6 Ω 时，出油口流量随时间的变化特性如图8 所示。在第15.9 ms、第17.2 ms、第20.5 ms时电磁阀阀芯落座，阀口流量降为0，电磁阀吸合时间分别为5.8 ms、7.1 ms、10.4 ms。随线圈电阻的增大，电磁阀吸合时间延长，响应速率变慢。

图8 线圈电阻对阀口流量的影响

利用单一变量控制法对电磁阀吸合时间的影响因素分析可知，电磁阀吸合时间对线圈电阻的灵敏度较大。

5.DOE-GA算法优化设计

5.1 理论分析

试验设计（Design of Experiment，DOE）是研究和处理多因子与响应变量关系的一种方法，通过建立响应与因子之间的函数关系，找出总体最优的改进方案，可用以下模型表征：

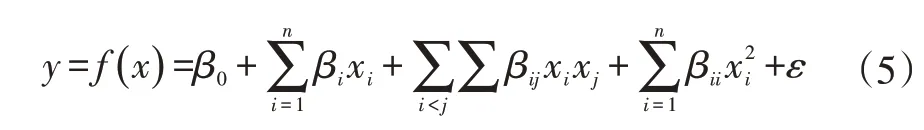
式中，为响应量；、β、β、β为系数；x、x为因子；(0,)为误差。

遗传算法（Genetic Algorithm，GA）以群体中的所有个体为对象，利用随机化技术对一个被编码的参数空间进行全局寻优，可简化为：

式中，为基本空间。

电磁阀的吸合、释放时间直接影响制动轮缸压力的变化率。本文利用DOE-GA 算法将电磁阀动作时间从阀的特性指标中提取出并作为最小化目标参数。选择弹簧刚度、线圈电阻、阀芯动铁总质量为优化参数，设定阀芯吸合和释放响应时间总和最短为优化目标。考虑到汽车实际工况和电磁阀特性，设定线圈电阻、阀芯总质量及弹簧刚度的约束区间为：

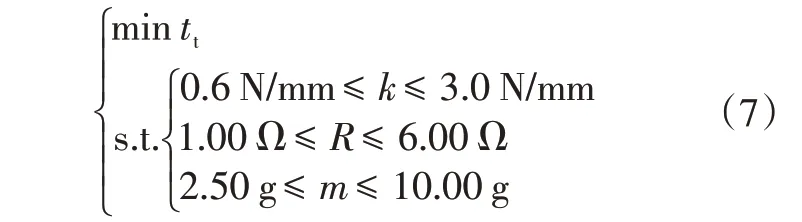
图9 详细阐述了优化过程，以电磁阀AMESim 模型为验证平台，通过DOE 获取弹簧刚度、线圈电阻、阀芯动铁总质量与阀芯吸合和释放时间的响应曲面模型，利用遗传算法对进行全局优化，寻找最佳个体，获取最佳弹簧刚度、线圈电阻和阀芯总质量。

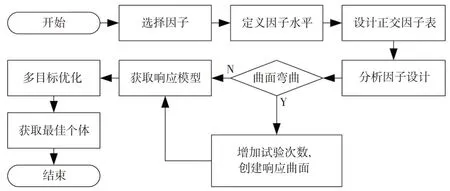
图9 DOE优化流程

5.2 变量因子正交试验规划

变量因子取电磁阀弹簧刚度、线圈电阻及阀芯总质量，响应变量为电磁阀吸合时间及释放时间。变量因子的限值如表3 所示，鉴于变量因子小于4 个，本文采用中心复合有界设计方法得到变量因子正交表，如表4所示。

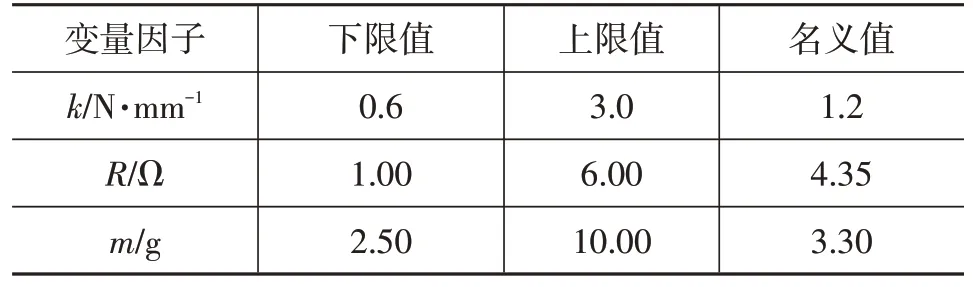
表3 变量因子两水平限值

5.3 响应曲面拟合及效果评价

针对表4，基于电磁阀模型得到如图10所示的试验结果，采用最小二乘法建立电磁阀吸合时间、释放时间与弹簧刚度、线圈电阻及阀芯动铁质量间的二阶响应曲面模型：

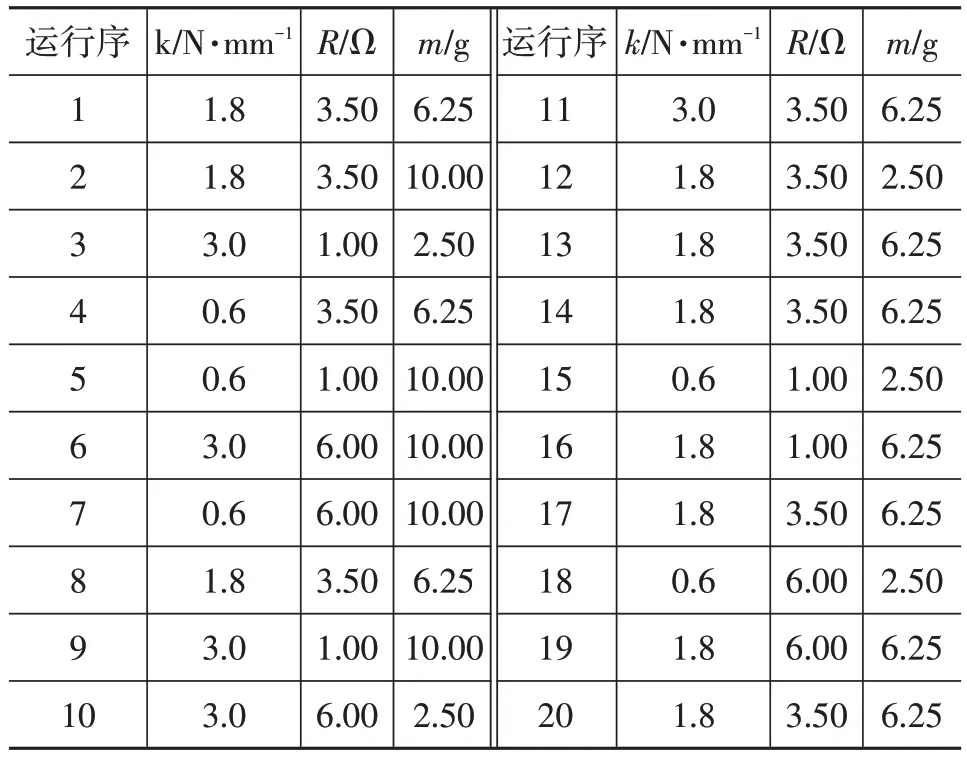
表4 三因子正交表

图10 正交试验结果

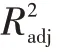
式中，为观测值的总数量；为模型中的项数（包括常数项）；为变异系数。

文中响应变量、的修正决定系数分别为99.88%、97.49%，说明响应曲面=(,,)及=(,,)的拟合精度较高。

5.4 优化结果分析

5.4.1 构造目标函数

以电磁阀吸合及释放的总响应时间最短构造目标函数，将电磁阀性能最优的实际问题转化为求函数极小值的数学问题：

式中，λ(=1,2)为响应量的重要度，本文取λ=1，表征、的重要度相同。

5.4.2 全局寻优

本文采用遗传算法对目标函数进行全局寻优，寻找最佳个体，获取最优变量因子。算法的迭代过程如下：

a.对解的基本空间进行编码。遗传算法在进行搜索前先将表示成遗传空间的基因型结构数据。

b.随机初始化种群。本文设定初始种群规模为50，由遗传算法通过初始种群生成函数随机产生。

c.计算种群的适应度。依据目标函数编写适应度函数，计算种群中个体的适应度，将适应度排序后编号。

d.生成子代。根据种群适应度均匀选择父代，父本中5%的精英个体直接遗传到下一代，杂交概率为80%。

e.适应度值评估检测，选择优良后代。计算交换产生的新个体的适应度，从交换后的群体中选出适应度好的个体，使它们有机会成为新的父代，繁衍下一代。

f.中止条件判定。依据设定的中止条件判定是否中止进化，若满足中止条件（本文设定的适应度函数值的偏差为10），则退出进化输出优化结果，否则跳转至步骤d。

图11 所示为电磁阀响应量遗传算法优化曲线，代数-适应度曲线表征在迭代38次后优化算法收敛，阀芯吸合和释放响应时间总和的最佳适应值为9.2 ms，此时变量因子弹簧刚度、线圈电阻及阀芯动铁质量分别为0.6 N/mm、3.84 Ω、2.5 g。

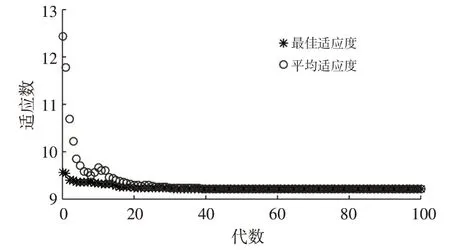
图11 遗传算法优化结果

为检验优化算法的有效性，本文将变量因子的优化值及名义值分别配置到模型中，电磁阀阀口流量响应时间如表5所示。

表5 优化前、后结果对比

由表5可知，优化后电磁阀吸合时间缩短14.1%，释放时间缩短5.1%，有效地提高了电磁阀的动态响应特性。上述结果表明，DOE-GA算法处理多变量交互作用下电磁阀响应特性优化问题具有可行性。

6 结束语

本文以常开式电磁阀的AMESim模型为研究对象，通过开关电磁阀响应测试台验证了所建模型的有效性。基于试验设计的建模方法，采用最小二乘法建立电磁阀吸合时间、释放时间与变量因子的高精度响应曲面二阶模型，利用遗传算对电磁阀结构参数进行优化，优化后电磁阀吸合时间缩短14.1%，释放时间缩短5.1%，有效地提高了电磁阀的动态响应特性。