丰盈“＝”内涵 发展代数思维

罗善彪 王珍丽

代数是一个推理运算的过程，需要学生应用数学符号、字母来研究运算规律，发现数学本质。代数是算术的一般化，许多算术内容蕴含着丰富的代数思想。算术思维侧重于通过数量的计算而求解，是一种比较直观的思维方式;代数思维则侧重于关系，表现为学生在具体情境中能把未知数当作已知数、与已知数共同参与运算的思维能力。在小学阶段培养学生代数思维已成为广泛共识。本期，我们来讨论如何培养学生的代数思维。

有研究表明：学生容易解决像“7+8=□”或“6+□=13”的等式问题，却很难解决像“17=8+□”或“5+□=9+4”的等式问题，其主要原因是学生适应顺向的算术思维，而不适应逆向的代数思维。究其原因，学生往往认为等号表示“运算结果”“要求计算答案”等，而不能從“对称”“平衡”“等价”的角度来理解等号的内涵，不能按“左右对称”或“两边平衡”“两边等价”来理解等式的意义。

基于上述分析，在小学阶段特别是小学低年级段，适当拓宽学生对等号内涵的理解，强化学生对等式的认识，促进学生建立等价模型，有利于学生早期代数思维的萌发，能为后续代数思维的学习和应用打下基础。笔者以北师大版数学教材为例，谈一谈相关教学设想和实践。

一、丰盈“=”认知，建立等价模型

学生第一次认识“=”，是在认识了部分数字（人教版数学教材安排在认识了1～5之后，北师大版数学教材安排在认识了0～10之后），有了基本的数感、符号意识和抽象能力之后，通过“比大小”的活动，与“>”和“<”等数学符号一起认识的。

教材呈现下图，引导学生按“一一对应”的思想方法比较小兔、篮子、胡萝卜、小猴、秋千的数量，进而引出“=”“<”和“>”，旨在使学生经历由物到数的抽象过程，认识到“=”表示两个量相等，进而抽象为表示两个数相等，帮助学生初步建立左右两边都是单一成分的“平衡”模型。

黄兴丰教授的研究表明：学生对等式中等号的理解可以划分成三个阶段，分别为指示阶段、动作阶段、等价阶段，处于不同理解阶段的学生，在分析和解决等式相关问题时的表现完全不同，同时，这三个阶段虽有区别，但并不是完全割裂的，它们在一定条件下可以自由转化，并能跳跃式发展。参照上述研究成果，在进行“=”的初始教学时，教师可以尝试直接从等价层面引导学生认识“=”，即在教学中反复引导学生用“一一对应”来体会和理解“=”表示“等价”的含义。教学过程略写如下。

“一只小兔和一个篮子对应，我们就可以将其看成一只小兔和一个篮子是等价的，用数学的方法表示是1=1”;

“两只小兔和两个篮子对应，我们就可以将其看成两只小兔和两个篮子是等价的，可以写成2=2”;

……

这样教学，能使学生认识到两个不同质的物品在量上可以等价，抽象成数可以相等，转化为数学符号就是“1=1”“2=2”等，进而从本质上认识“=”，建立“等价”模型。

二、重构等式引入，体会等价意义

学生对“等式”的认识是伴随着“加减法的初步认识”一同发展的。刘加霞教授的研究表明：现行各版本教材所设计的“加法的初步认识”情境，一般先呈现部分与部分的聚合，即“合并”情境;而“减法的初步认识”情境一般是一元动态情境，即“取走”情境。这两种情境虽然比较契合正整数加减法的现实意义，容易被学生掌握和理解，但不能很好地解释等号的等价意义，不利于学生代数思维的培养。史宁中教授对此有相关建议，他指出：加法的初步认识应该采用相等模型引入，而不是变化型（或合并型）。基于此，在教学“加法的初步认识”时，教师可以做如下教学改进：除了遵从教材原意正常引入“3+2=5”的等式，还可以对“试一试”中的教学素材进行情境重构，引导学生体会等号的等价意义。

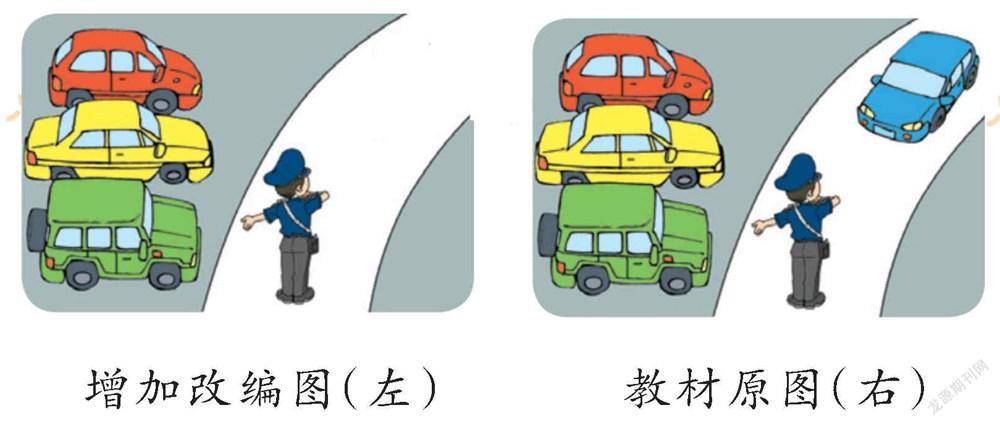
例如，教师可以同时出示如下两幅情境图，然后提出相应问题：左右两幅图中的车一样多吗？怎样才能使两边的车一样多呢？

通过这两幅图的比较，学生可以直观感知到，左边也要再开来一辆车，才能使两幅图中的车一样多，即两幅图中车的数量相等。像这样自然而然地渗透等号的等价意义，可以很好地解释“3+1=4”，帮助学生跳出“等号是运算符号、等号右边表示运算结果”的思维定式，感悟等号的本质含义。

教学中，我们除了可以对这幅情境图进行重构，其他的情境图包括减法的引入情境，都可以进行类似的重构，以深化学生对等式和等号的理解和认识，促进学生代数思维的萌发。

三、丰富等式类型，培养等价意识

纵观小学数学教材，学生从第一次认识等号、第一次学习加法开始，直到四年级（人教版教材是五年级）学习方程时，才出现“等式”这个名词，而且在这四年左右的时间中，教材也没有呈现等式的描述性概念。学生对“算式”“等式”等概念认识模糊，理解不深刻，直接导致学生对“代数式”的不认可和不理解，进而发展为对代数思维的不接纳。其直接原因就是学生对等号的认识不全面，理解不深入，从而陷入认识误区：等号就是一个运算符号，等号的出现相当于预示着某个运算结果的产生，等式就是算式，等式中的等号只是表示要做某运算等。

基于上面的分析，我们在教学中除对“=”加强理解，对“算式”“等式”等概念提前渗透之外，还要强化对“等式”的变式引入，以丰富学生对等式类型的认识，培养学生的等价意识。如在加减法等式成功引入后，我们可以对教学情境图做一些变形修改，或借助数的分解知识，形成“5=3+2”“1=5-4”“8=1+3+4”等形式的等式，促进学生树立数与式等价的意识。

另外，在教学“加法表”“减法表”时，我们可以借助表格引出“5+5=3+7”“9-3=7-1”“4+2=9-3”等两边都有算式的等式结构，甚至还可以引出多个算式连等的长等式，以此培养学生整体认读等式的习惯，促进学生以算式作为一个整体的等价模型的建构。

在后续较复杂的计算教学中，我们可以有意识地呈现各种类型的等式，加深学生对等价模型的理解，还可以利用“递等式”的运算方式，尝试进行“恒等运算”，如“304÷5-254÷5=（304-254）÷5=50÷5=10”（此题的解答过程，若按常规的“递等式”形式计算，就是一种运算程序;若写成这样的长等式，则可以表示一种恒等变化），为后续学生自主运用等式的性质解方程做铺垫。

（作者单位：罗善彪，宜昌市教育科学研究院;王珍丽，枝江市南岗路小学）

[此文系湖北省教育学会“十四五”立项重点课题“小学数学教学中渗透代数思想的案例研究”的研究成果。课题编号：A03-01]

责任编辑  刘佳