数学问题情境化设计策略
2022-04-27夏小刚张晶
夏小刚 张晶

情境化问题是学生核心素养形成、发展和表现的载体。核心素养取向下的小学数学教学应该以情境化问题为载体,让学生在特定的情境中运用数学思维解决问题,实现数学素养的发展。但在数学问题的情境化设计中,普遍存在“重虚拟情境、轻真实情境”“重学生自主探究、轻教师启发引导”等现象。导致这些现象的原因,从根本上可以归结为数学问题情境化设计中的意义缺失。为此,本文将从学习意义的视角,探讨数学问题情境化设计的基本策略。
一、学习意义:数学问题情境化设计的纽带
学习是学习者主动追寻意义与创造价值的过程。追问学习的意义,是数学教育的应有之意。“意义”是一个有多种含义的概念。在现代汉语中,意义有两个层面的含义:一是语言文字或其他信号所表示的内容;二是“价值,作用”,如“一切存在的事物都是有意义的”等。在心理学上,意义则被看作是一种“心理表征”或“意义表征”,即个体在组织和理解内容时内心生成的内容框架。对于数学问题的情境化设计而言,“有价值、有作用”的重要前提在于情境化问题能引发学生的认知冲突,促进学生数学思维的发展。
学习意义是联结数学问题情境化设计要素的纽带。具体地说,就是立足于学生的现实,将学生主动的意义建构链接到情境素材、问题表征、数学任务、设计意图等要素的整合中,使其在情境化问题探索中得到意义确认与价值认同。由此形成的情境化问题蕴含着教师的教学期待:学生在情境化问题的观察、探究、猜想、验证与证明的活动中,构建知识,发展思维,促进数学素养的生成。然而,当嵌入的情境内容外在于学生的生活经验时,那些被教师认为具有价值的情境化问题,却不一定对学生构成意义。下面,笔者以“居民用水”问题为例说明。
某城市制定了居民用水标准,超标部分加价收费。如果在标准水量内,每立方米的水费是1.4元,超标部分每立方米的水费增加100%。该城市小明家有三口人,五月份用水15立方米,交水费25.2元。该城市三口之家每月用水量最高标准规定为多少立方米?
这是一个涉及小数四则混合运算的情境化数学问题。其中,“居民用水”是情境,算出“该城市三口之家每月用水量最高标准”是任务。然而,“该城市三口之家”的文字表述,容易导致学生对“家庭每月用水量最高标准”的理解不清,譬如,与“三口之家”相比,“四口之家”每月用水量最高标准是否就不一样呢?“五口之家”呢?无疑,这种说法与城市居民生活用水普遍实行的“一表一户”收费制相抵触。换言之,该情境化问题由于其嵌入的情境内容与学生的生活经验不太一致,难以对学生小数四则运算知识的应用产生积极作用。
上述问题情境化设计中的意义缺失,折射出数学认识观所带来的制约和影响。事实上,随着强调纯数学的基础主义向拟经验主义的转变,人们认识数学的关注点转移到了数学的应用。正如学者谢明初所说,欧几里得几何的价值之一是欧几里得运用了公理化方法,而公理化方法正是由人们在做数学过程中所使用的演绎推理发展而来,也就是说,公理化方法是在人的经验基础上产生的。他还提出,数学的价值在于,它为居住在地球上的人类的利益服务。在这种数学认识观的影响下,数学知识似乎具有了自明的有用性,只要掌握了这些知识,便可以将它们运用到各种不同的情境中去认识世界、解决问题。基于此,在情境化问题设计中,当源自人类经验活动的数学知识被排斥在学生的经验世界之外,或者说,当学生的经验世界被排斥在情境化问题认识活动之外,学习意义的缺失将不可避免。
二、基于学习意义的数学问题情境化策略
学习意义在问题情境化设计中的重要意义,凸显了对教师设计情境化问题的基本要求,即只有立足于学生的生活经验、活动经验和思维经验,数学问题情境化设计才能将学生的数学认识与探究活动置于学生的经验世界中,产生数学学习的意义。为此,笔者将从学生的生活经验、活动经验和思维经验等视角,探析数学问题情境化设计的基本策略。
1. 对接生活经验,还原知识的经验性内容
数学问题的情境化,强调将数学问题置于数学知识发生发展的经验性情境中。对接学生的生活经验,旨在让学生的生活经验在情境化问题中能够以经验性内容的方式存在,并被数学活动“唤醒”,成为学生观察、探索、猜想、验证和证明等操作性活动的背景和条件。
如在“认识分数”教学中,一位教师设计了这样一个情境化问题:2瓶雪碧,1个苹果,想把这些东西平均分给2名小朋友,怎样分才公平呢?学生带着愉快的生活体验,兴致盎然地进入学习分数的状态中。当学生思考将1个苹果平均分给2名学生,发现“半个、半块、一半”不能用以前学过的数来表示时,引发了学生强烈的认知冲突,使他们深刻地认识到分数源于生活需要。在通过平均分苹果得到这个苹果的[12]之后,教师设计了“用笔涂出图形(花瓶图形、脸谱图形)的[12]”的情境化问题。上述活动中,无论是苹果的分配还是“涂图”活动,都是学生在生活中经历过的活动和熟悉的认知对象,这些生活经验不仅可以激发学生学习的积极性,增进学生对分数概念的理解,而且可以丰富学生的数学活动经验。
数学问题的情境化设计,目的在于促进学生的数学认识,发展学生的数学素养。然而,皮亚杰指出:“认识既不是起因于一个有自我意识的主体,也不是起因于业已形成的,会把自己烙印在主体之上的客体;认识起源于主体与客体之间的相互作用,这种认识发生在主体和客体之间的中途。因而同时既包含着主体又包含着客体……”学习是由经验所引起的行为或思维的比较持久的变化,因此,对接学生的生活经验,聚焦学生的“学习经验”,成为数学问题向经验性内容转化的关键。
2. 立足活动经验,整合情境化问題中的知识与技能
张奠宙教授认为,数学并不完全是从现实生活情境中直接产生的,人们除了依靠日常生活经验,还必须通过一些感性或理性的特有的数学活动,才能把握数学本质、理解数学意义。无疑,直接联系日常生活经验的数学活动,或通过创设问题情境所开展的间接数学活动,都属于“特有的数学活动”范畴,学生的数学活动经验是在这些特有的数学活动中产生的。数学素养是“学生在今后的生活、学习和工作中所需要的数学知识与技能(PISA)”,而数学素养的发展离不开数学活动经验的积累,因此,立足于学生的数学活动经验,整合情境化问题中的知识与技能,成为数学问题情境化设计的一种重要方式与方法。为此,教师需要在数学问题情境化设计中优化素材,毕竟,好的素材能唤醒学生原有的数学活动经验,帮助学生主动运用经验去解决新问题。
如在《平行四边形的面积》教学中,一位教师立足于学生的活动经验,将平行四边形面积的计算方法与技能进行整合,设计了如下情境化数学问题:
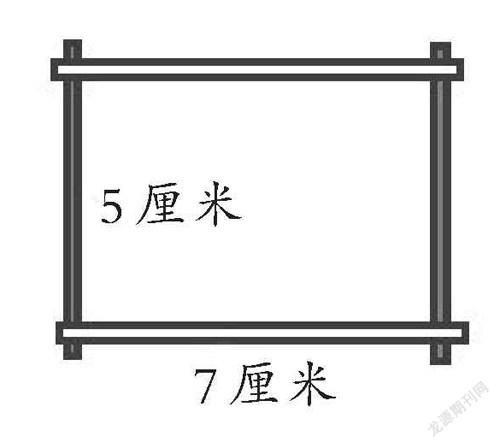
①如下图所示,这个长方形的长是7厘米,宽是5厘米,它的面积是多少?如果拉动长方形的对角,会变成什么形状?面积会发生变化吗?
②将原长方形和新平行四边形准确地画在教师提供的方格纸上,通过数方格的方式来确定图形的面积是否发生了变化。
……
学生利用方格纸、小木棍等素材,通过数方格大致估算了图形的面积,并在小组内交流计算平行四边形面积的方法,进而发现周长相同的长方形和平行四边形的面积不同。在此基础上,教师进一步引導学生通过“裁剪拼补”探究平行四边形面积的计算方法。其中,周长与面积之间关系的探究活动,不但暴露了学生的原有经验,引发学生思维碰撞,也让学生的数学核心素养在探究中萌发。
3.结合思维经验,赋予情境化问题所需要的难度水平
赋予情境化问题什么样的难度水平,取决于教学任务的需要。一个好的情境化问题,应该体现教师对其难易度的良好把控。这就需要教师调整解决情境化问题所需要的知识和技能,既不能让问题的解决显而易见,也不能让问题的解决非常复杂或需要新知的加入。为此,教师可以结合学生的思维经验,通过以下两种基本方法,赋予情境化问题所需要的难度水平:第一,强化(或削弱)问题情境的数学特征;第二,增加(或减少)问题所依存的背景信息的复杂性。其中,“强化(或削弱)”“增加(或减少)”反映了教师对教学内容的教学加工,其教学加工的强弱程度,取决于教学任务的靶向需求和学生已有的思维经验。如在“长方形的周长”教学中,一位教师设计了这样的问题:用篱笆围一块长方形菜地,已知菜地宽80米,长100米,需要用篱笆多少米?显然,学生直接用长方形周长公式就能计算篱笆的长度。为了增强问题的数学特征,教师将问题中的数学信息“长100米”改为“长比宽多10米”,这样,要计算篱笆的长度,就得先求出菜地的长。教师同时改变了问题情境的数学信息和背景信息,得到一个新问题:用篱笆围一块长方形菜地,已知菜地宽80米,菜地一面靠墙,并且宽与长的比是3∶4,需要用篱笆多少米?这三个数学问题的情境化设计,使其数学特征愈加凸显。
另外,数学问题情境化设计必须重视学生思维过程的组织:一方面,提供感性材料,通过问题情境化设计,将抽象化为具体、一般化为特殊;另一方面,注重情境化问题设计的层次性和递进性,由此形成的情境化“问题链”不仅要有利于不同思维经验的学生参与,而且要使学生在思考逻辑递进问题的过程中得到思维经验的拓展。不过,情境化问题的难易水平是否贴近学生的思维经验,是否符合学生思维发展的需要,是一个具有很大主观性的问题。教师要通过调查、分析典型学生把握学情,增强自身的教学判断力。
(张晶,贵州师范大学博士生,琼台师范学院教师)
[本文系全国教育科学“十三五”规划课题“面向核心素养的数学问题情境教学测评模型研究”的研究成果。课题编号:XHA180286]
责任编辑 刘佳
