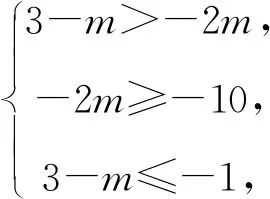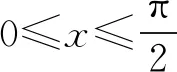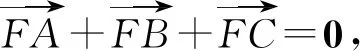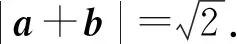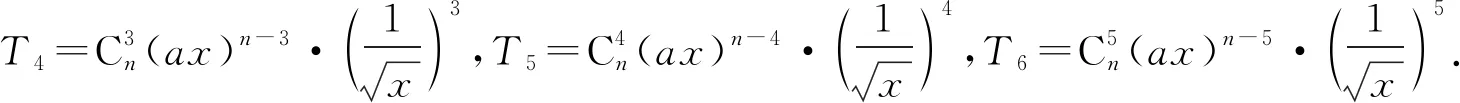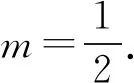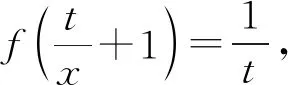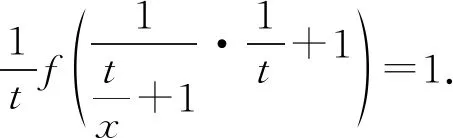2022年高考模拟试题(二)
2022-04-26李小蛟
李小蛟
(四川省成都市树德中学 610091)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).

A.0 B.1 C.-1 D.2
2.集合A={x|-2m
A.3 B.7 C.15 D.63
3.某学生设计了一个随机点名的程序,其流程如图1.RAND表示[0,1]内产生的随机数,[x]表示不大于x的最大整数,如[3.2]=3.每一次输出的值代表某位同学的学号(0-39号).要使每个同学被抽到的概率相等,则“?”处应填入的内容是( ).

图1
A.a=[9a] B.a=[10a]
C.a=[3a] D.a=[4a]
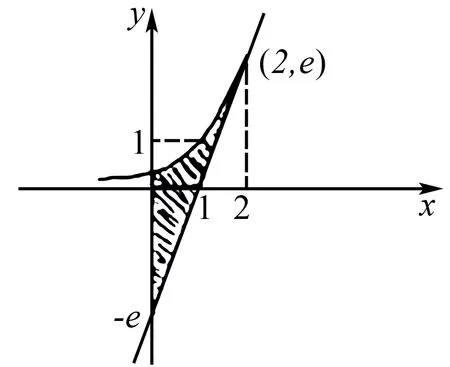
4.函数f(x)=ex-1,过(2,f(2))作关于y=f(x)的切线l,求y=f(x)与l与y轴所围成的图形的面积为( ).
5.f(x)=cosx+2|cosx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是( ).
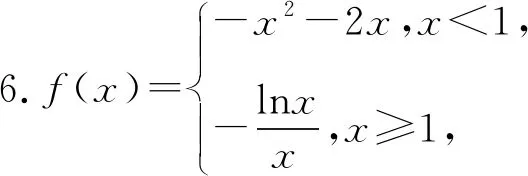

A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
8.下列说法中,错误的有( ).
(1)空间中到定点的距离等于定长r的点的集合,构成半径为r的球.
(2)M是两条异面直线m,n外一点,则过点M且与m,n都平行的平面有且只有一个.
(3)α,β,γ是三个不同的平面,l,m,n是三条不同的直线.若α∩β=l,β∩γ=m,α∩γ=n,则l∥m∥n.
A.0个 B.1个 C.2个 D.3个
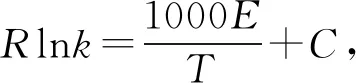
A.14.2J/(mol·K) B.12.9J/(mol·K)
C.13.6J/(mol·K) D.10.8J/(mol·K)
10.a,b,c为单位向量,且a·b=0,(a-c)·(b-c)≤0,则|a+b-c|的最大值为( ).

A.b>a>cB.c>a>b
C.c>b>aD.b>c>a


二、填空题(本大题共4小题,每小题5分,共20分.)





三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.)
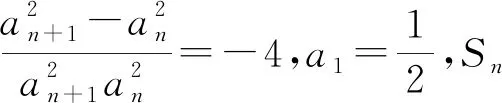
(1)求{an}的通项公式;
(2)求Sn.
18.(理科)如图2,AB=AD=2,△ABD为等腰直角三角形.ΔABF为正三角形.E,F分别位于平面ABD两侧,EC⊥平面ABD,且EC中点G在平面ABD上,CD=BC,二面角B-EC-D为60°,EC=2.
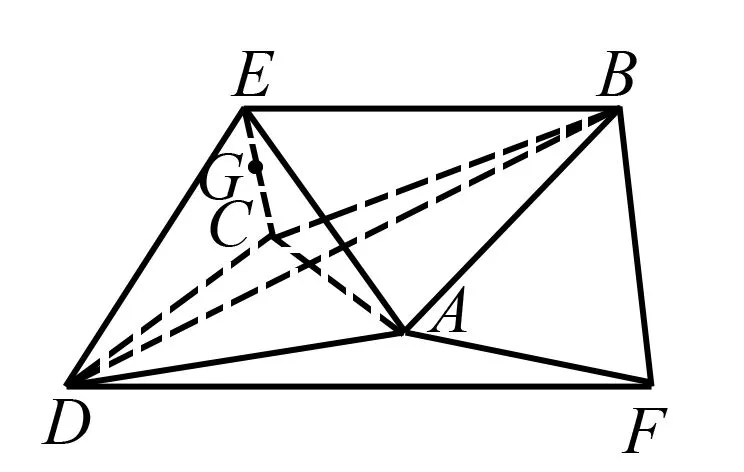
图2

(2)在(1)的条件下,求多面体EABGDF体积.
(文科)在如图3所示的多面体中,ABCD是正方形,A,D,E,F四点共面,AF∥面CDE.
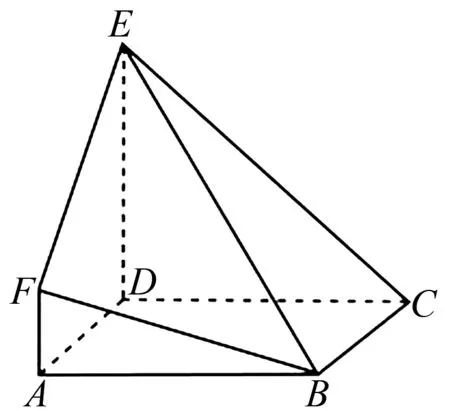
图3
(1)求证:BF∥面CDE;
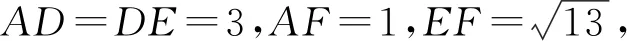
19.(理科)2020年初,新型冠状病毒在中国肆虐横行.为防止疫情进一步扩散,人人居家防疫,出门戴口罩.同时,为缓解口罩供不应求的情况,多数企业纷纷转战口罩生产.然而,不合格的口罩非但无防护作用,还会引起皮肤过敏等一系列不良反应.为了调查某企业生产的口罩质量,调查人员在该企业第一天内生产的口罩中随机抽取了40个,通过检测获得了各个样品的质量指数Z,并绘制成以下表格.

质量指数[1.5,2.5)[2.5,3.5)[3.5,4.5)[4.5,5.5)[5.5,6.5)[6.5,7.5)[7.5,8.5)频数16810942
(1)求该批样品质量指数的平均值(同一组数据用该组数据的中点值表示).
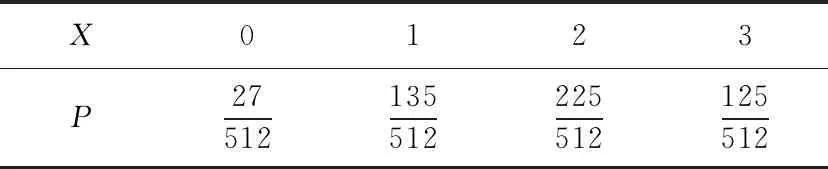
(2)调查人员又在该企业第二天生产的口罩中抽取了3个,其中质量指数在[1.5,2.5)的个数为X.求X的分布列和期望.(将第一天生产的口罩中各质量指数的频率视为概率)
(3)进一步调查表明,在正常生产状况下,该企业一天中生产的口罩指数Z可近似地看作服从正态分布N(μ,2.25).期中μ近似为(1)问中求出的平均值.
①在正常生产条件下,求P(3.5 ②第二天抽取的3个口罩中,检测出了质量指数在(0.5,9.5)之外的口罩,于是调查人员判断当天生产状况出现了异常,需进一步检查.请根据相关数据说明该判断的合理性. 参考数据:P(μ-σ (文科)某医疗机构承担了某城镇的新冠疫苗接种任务.现统计了前8天每天(用t=1,2,…,8表示)的接种人数y(单位:百)相关数据,并制作成如图4所示的散点图: 图4 (1)由散点图看出,可用线性回归模型拟合y与t的关系,求y关于t的回归方程(系数精确到0.01); (2)根据该模型,求第10天接种人数的预报值;并预测哪一天的接种人数会首次突破2500人. (1)求椭圆C的方程, 21.已知函数f(x)=(x-1)lnx-x+1. (1)求f(x)在(1,f(1))处的切线方程以及f(x)的单调递增区间. (2)f(x)在(1,+∞)内零点为x=x0,曲线y=f(x)在(x0,0)处切线方程为y=g(x).证明:f(x)≥g(x). (1)求C1的极坐标方程; (2)设点M,N在C1上,点P在C2上(异于极点),M,N,P在第一象限.若O,M,P,N四点依次在同一条直线l上,且|MP|,|OP|,|PN|成等比数列,求l的极坐标方程. 23.【选修4-5:不等式选讲】设a,b,c为正实数,证明: 参考答案 2.B.(1)若A=φ,则3-m≤-2m,得m≤-3.又m>-4,m∈Z,故m=-3. 3.D.由b=[10b]可知0≤b≤9.又因为S=10a+b,所以0≤a≤3.而[x]表示不大于x的最大整数,所以a=[4a]才满足要求. 4.B.因为f′(x)=ex-1,所以f′(2)=e. 所以直线l方程为y=ex-e.所以f(x)与切线的图象如图5所示,所围图形即阴影. 图5 5.A.因为f(x)=cosx+2|cosx|,x∈[0,2π], f(x)=cosx+2cosx=3cosx. 所以当1 8.D.①构成的是半径是r的球面,而不是球,故错误;②在直线m上取一点P,过P作直线l//n,则直线m,l确定一个平面α,取M∈α,则过点M不能作平面同时与m,n平面平行,故错误;③正方体中相交的两个侧面同时与底相交,但得到的三条交线并不平行,故错误. 解得1000E=21000. 13.画出满足条件的区域,如图6: 图6 2x+y的最小值为1,即y=-2x+a与满足条件的平面区域有交点时的最小截距为1. 所以y=m=-1. 又因为AC≤BC,所以由正弦定理知: sinB≤sinA. (2)bn=4an-1·an·an+1, 设F(1,y0,z0)(z0<0), 平面ABD法向量n(0,0,1), (2)由EC⊥平面ABD, 所以VEABGDF=VE-ABGD+VF-ABGD (文科)(1)由ABCD是正方形,可知AB∥DC. 而AB⊄面CDE,所以AB∥面CDE. 又AF∥面CDE,AB∩AF=A, 所以面ABF∥面CDE. 又BF⊂面ABF,所以BF∥面CDE. (2)因为AF∥面CDE,AF⊂面ADEF, 面CDE∩面ADEF=DE,所以AF∥DE. 在线段ED上取点G,使得EG=2, 于是DG=1=AF,而AF∥DG. 所以四边形ADGF是平行四边形. 于是EF2=EG2+FG2,即FG⊥EG,则AD⊥ED. 因为四边形ABCD是正方形,有AD⊥DC, 而DC∩DE=D,所以AD⊥平面CDE. 故该批样品质量指数的平均值为5. 故分布列为 X0123P27512135512225512125512 ②3个口罩的质量指数均在(0.5,9.5)之内的概率P1=0.99743≈0.9922.故出现该范围外口罩的概率.P2=1-P1=0.0078. 该概率很小,因此一旦发生这种情况,就有理由认为当天生产可能异常,需进一步检查. (文科)(1)由题意,得 ≈1.667, 20.(1)如图7,设P(x0,y0),M(x1,y1),N(-x1-y1),E(x1,0), 图7 由题知 |AB|=2a=4,解得a=2 (2)设AG:y=k(x+2),BH:y=k′(x-2). (4k2+1)x2+16k2x+16k2-4=0, 显然Δ>0. 化简,得4kk′2+12k2k′-k′-3k=0. 即(4kk′-1)(k′+3k)=0. 易知kk′<0.故k′=-3k. (2)f(x)=(x-1)lnx-x+1=(x-1)(lnx-1). 故φ(x)在(0,e)单调递减,在(e,+∞)单调递增. 故φ(x)≥φ(e)=0,即f(x)≥g(x). 同理有x2′≥x2. 由-x1′+1=m,得x1′=1-m. 22.(1)C1直角坐标方程(x-a)2+y2=3. 即x2+y2-2ax+a2-3=0. 由x2+y2=ρ2,x=ρcosθ, 得ρ2-2aρcosθ+a2-3=0. 又因为a>0,故a=2. 故极坐标方程为ρ2-4ρcosθ+1=0. (2)l的极坐标方程θ=x(ρ∈R), 设M(ρ1,α),N(ρ2,α),P(ρ3,α), 则ρ1<ρ2. 则ρ1+ρ2=4cosα,ρ1ρ2=1. 因为|MP|,|OP|,|PN|成等比数列, 即2cos2α=4cos2α-1, 当a=b=c时取等号. (2)由(1)知 当a=b=c取等号.