对一道高考客观压轴题的研究与备考建议
2022-04-26刘海涛
刘海涛
(安徽省芜湖市第一中学 241000)
《中国高考评价体系》指出:“高考要求学生能够触类旁通、融会贯通,既包括同一层面、横向的交互融合,也包括不同层面之间、纵向的融会贯通”.在教学过程中,对于一些典型问题,尤其是高考真题,如果我们能够从不同角度思考,寻求不同的解法,以一题多解的方式寻求知识间的内在联系,构建知识的网络体系,加深对问题的本质认识,定会拓宽解题视野,发散解题思维,提升学习兴趣,提高解题能力.本文是笔者对一道高考真题的研究,现与读者分享交流.
1 真题呈现与分析

A.a 分析该题形式上以对数式和根式为载体,考查比较实数的大小关系,试题结构虽简单、明了,但综合性强、内涵丰富,主要考查对数的运算性质,构造函数比较大小,不等式的性质等知识,体现了逻辑推理、数学运算等数学核心素养,强化了综合运用所学知识分析问题、解决问题的能力. 解析因为1.012=(1+0.01)2>1+2×0.01=1.02,所以a=ln1.012>b,于是排除选项A,D.余下的选项A,C只需比较a,c大小即可. 由(1+x)2-(1+4x)=x(x-2)<0,得 则f′(x)>0,函数f(x)在(0,1)上单调递增. 有a-c=f(0.01)>f(0)=0. 即a>c.故选B. 则f′(x)>g′(x)>0,函数f(x)和g(x)在(0,1)上都单调递增,但函数f(x)的增长快于函数g(x),于是a=f(0.01)>g(0.01)=c,故选B. 评注根据a,c的数式特征,构造两个函数f(x)和g(x),注意到f(0)=g(0)=0后,根据函数的增长率大小来比较大小,方法巧妙新颖,过程简洁,给人耳目一新的感觉.实际上,可以再根据b的数式特征构造函数h(x)=ln(1+2x),比较三个函数的增长率便可直接得出答案,如图1,为三个函数在区间(0,1)上的图象. 图1 思路3由于a,c分别为对数式与根式,不易直接比较大小,不难思考利用中间量比较大小. 显然f′(x)>0,函数f(x)在(1,+∞)上单调递增,所以f(1.01)>f(1)=0. 即a>c.故选B. 显然f′(x)>0,函数f(x)在(0,+∞)上单调递增,所以f(0.01)>f(0)=0. 即2ln1.01>0.02-0.0001.即a>c.故选B. 评注该法借助泰勒展开式对a,c进行估值,通过估值比较大小.作为选择压轴题,该题具有高等数学知识背景,若我们适当了解一些泰勒展开式的有关知识,则可“高观点”地分析问题、解决该题,使得解答过程简洁明了. 通过上述解答,我们不难发现该题蕴含了如下不等式: (1)伯努利不等式:(1+x)α≥1+αx(x>-1,α>1,当x=0时等号成立). 我们在比较a,b大小时,实际是比较1.012与1.02的大小,事实上(1+0.01)2>1+2×0.01,即1.012>1.02. 在日常的解题教学中,我们不能仅止步于问题的解决,而应该教会学生从不同的角度去分析问题,寻求不同的解法,通过一题多解发现知识间的内在联系,体会知识间的转化与化归,构建知识间的网络体系.本题中,我们从五个角度思考问题,给出5种比较实数a,c大小关系的方法,其中方法1从函数单调性的角度比较大小;方法2从函数增长率的角度比较大小;方法3和方法4利用中间量比较大小,分别介绍了两种寻找中间量的不同方法;方法5基于高等数学泰勒展开式的“高观点”,利用近似值比较大小.得到以上不同解法,思维方式的不同带来解答形式的不同,给考生极大的思考与解答空间,在运算量和解答时间上出现差别,区分出不同层次的考生,具有很好的信度与区分度. 《普通高中数学课程标准(2017年版)》指出:在数学高考命题中,考查内容应围绕数学内容主线,聚焦学生对重要数学概念、性质、方法的理解和应用,强调基础性;注重数学本质和通性通法.在高考备考教学中,教师应加强基础知识、基本技能和基本数学思想方法的训练.我们寻求一题多解,但不能满足于一题多解,对于一些常考题型,甚至于必考题型,教师要指导学生总结该类问题的通解通法,形成解题模型.近些年,高考卷中对指、对、幂函数值大小比较的考查,重要集中在指对互化,三类函数的运算性质、图象、单调性、不等式的相关性质等知识,难度有加大趋势,基本集中在选择题后三题中.因此,重视指、对、幂函数的图象与性质的掌握,作差、商比较大小,函数单调性法、图象法、中间量法等方法的训练,只有扎实掌握了这些通性通法,在高考中才能“以不变应万变”. 高考试题凝聚着命题人的心血与智慧,是命题者反复考量与打磨才成型的,对教师的教学具有导向性与启示性.对高考题进行深入研究,挖掘命题背景,也是教师日常教研的一项基本任务,反映了教师本身的业务素养与能力.笔者通过对问题的解法进行探究,挖掘出试题蕴含的不等式背景,若日常的备考中,教师能指导学有余力的学生适当掌握一些常见的不等式模型,甚至适度了解一些高等数学的知识,这样在遇到一些以特殊模型或高等数学知识为背景命制的考题时,学生才能快速看清问题的本质,找准解题的方法,顺利完成考试.2 解法探究








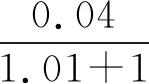






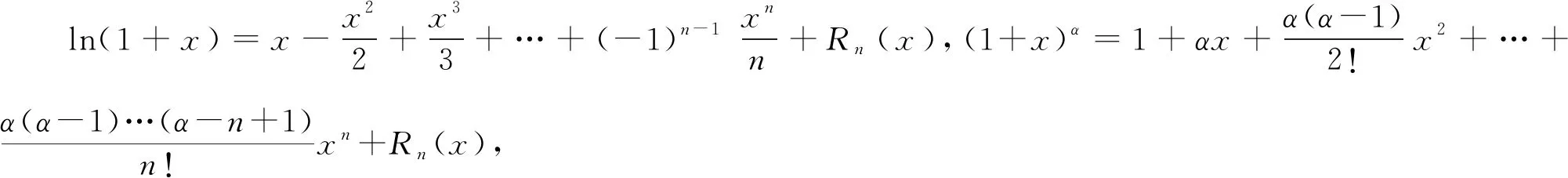
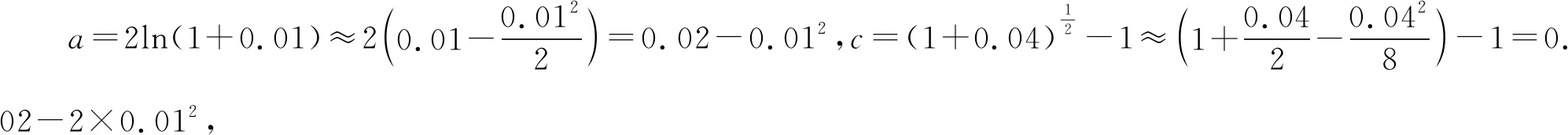
3 试题蕴含的背景不等式





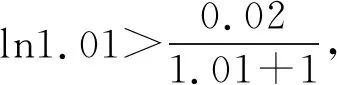

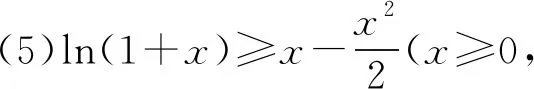

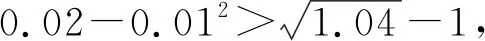
4 高考备考建议
4.1 多角度思考问题,寻求一题多解
4.2 注重通性通法,以不变应万变
4.3 探寻问题蕴含背景,看透问题本质
