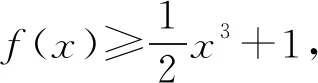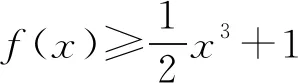借助构造法 解答高考数学题

杨蓓蓓 王 佳

(安徽省阜阳市红旗中学 236000)

近年来高考数学习题对构造法的考查较为频繁.很多学生不注重构造法的应用，导致在解题中走了不少弯路，因此，教学中为使学生认识到构造法在解题中的重要性，掌握运用构造法解题的相关技巧与细节，有必要为学生讲解构造法在高考数学解题中的应用.

1 构造法解不等式习题

不等式是高中数学的重要知识点，相关习题的解题思路灵活多变.教学中为避免学生思维定势，掉进命题人设置的陷阱之中，既要注重与学生一起总结不等式习题解答思路，又要示范构造法的应用，使学生体会构造法在解题中的便利，更好地把握相关习题特点，逐渐提升其运用构造法解题的意识.

例1(2020年全国Ⅱ卷第12题)若2x-2y<3-x-3-y，则( ).

A.ln(y-x+1)>0 B.ln(y-x+1)<0

C.ln|x-y|>0 D.ln|x-y|<0

该题目给出的已知条件较为简单，但却考查了指数函数、对数函数、函数单调性、构造法等知识点，是一道不错的好题.

解析因为2x-2y<3-x-3-y，

所以2x-3-x<2y-3-y.

令f(t)=2t-3-t，因为2t为增函数，-3-t为增函数，所以f(t)为增函数.

又因为f(x)=2x-3-x

所以x

即y-x>0，y-x+1>1.

由对数函数性质可知，ln(y-x+1)>0.

而y和x的大小未知，因此无法判断|x-y|，|x-y|和1的大小关系.故选A.

2 构造法解方程习题

方程与函数有着密切的联系，在解答方程类的问题时常常将其转化为函数问题.但高考中的部分习题综合性较强，不容易直接观察出相关参数之间的内在关系，因此，解题中应具备灵活的思维，积极联系所学基础知识，通过观察方程特点构造出相关函数，运用函数性质加以巧妙突破.

例2(2020年全国Ⅰ卷)若2a+log2a=4b+2log4b，则( ).

A.a>2bB.a<2bC.a>b2D.a

该题目属于函数与方程综合题目，具有一定难度.解答该题需要具有灵活思维，能够从给出的已知条件中找到突破口.观察给出的等式形式可知需要运用构造法进行解答.

解析令f(x)=2x+log2x，因为2x，log2x均为单调递增函数，所以f(x)为增函数.

观察给出的四个选项，可令

F(x)=f(a)-f(2b)=2a+log2a-22b-log22b，

又因为4b=22b，2log4b=log2b，

2a+log2a=4b+2log4b，

所以2a+log2a=22b+log2b.

所以F(x)=22b+log2b-22b-log22b

=log2b-log22b

所以a<2b，故选B.

3 构造法解数列习题

数列相关知识较为抽象，是高中数学的难点知识.相关习题在高考中常作为压轴题，考查学生对数列知识的理解深度以及灵活运用程度.教学中为提高学生解答不同数列习题的能力，应优选高考中代表性较强的题目，做好构造法的应用讲解，使学生更好地把握数列知识本质，掌握构造法解答数列习题的思路，在解题中能够融会贯通、举一反三.

例3(2019年全国Ⅱ卷)已知数列{an}满足a1=1，b1=0，4an+1=3an-bn+4，4bn+1=3bn-an-4.

(1)证明：{an+bn}是等比数列，{an-bn}是等差数列；

(2)求{an}和{bn}的通项公式；

解答该题目可从要求解的问题入手进行分析，从中可以看到需要运用构造法进行解答.

解析(1)因为4an+1=3an-bn+4，

①

4bn+1=3bn-an-4，

②

①+②整理，得

4(an+1+bn+1)=2(an+bn).

又因为a1+b1=1，

③

①-②整理,得

4(an+1-bn+1)=4(an-bn)+8.

所以(an+1-bn+1)-(an-bn)=2.

又因为a1-b1=1，

所以{an-bn}是以1为首项，以2为公差的等差数列.

即an+bn=1+(n-1)×2=2n-1.

④

(2)③+④,③-④整理,得

4 构造法解导数习题

构造法在解答高中数学导数习题中有着广泛的应用.教学中为提高学生运用构造法解答导数学习的能力，一方面，为学生总结导数习题中常用的构造思路，并在课堂上通过设计问题与学生互动，使其更好地把握构造法应用的相关细节.另一方面，与学生一起分析相关的高考习题，使其明确高考导数习题的考查知识点、考查方向，使其深刻体会构造法在解题中的具体应用，以后遇到相关习题，能够迅速、正确地构造出相关函数，实现顺利解题.

例4(2020年全国Ⅰ卷)已知函数f(x)=ex+ax2-x.

(1)当a=1时，讨论f(x)的单调性；

该题目中的第(1)问考查学生灵活运用导数研究函数单调性问题，第(2)问考查学生运用构造法求函数最值问题.

解析(1)因为f(x)=ex+x2-x，则

f′(x)=ex+2x-1.

则f″(x)=ex+2>0.

所以f′(x)在R上单调递增.

又因为f′(x)=0时，x=0，

则当x<0时，f′(x)<0；

当x>0时，f′(x)>0.

即f(x)的递减区间为(-∞，0)，递增区间为(0，+∞).

(2)当x=0时，f(x)=1≥1成立，此时a∈R；

问题转化为求h(x)的最大值，则

则g′(x)=ex-x-1，g″(x)=ex-1>0，表明g′(x)单调递增.

又因为g′(0)=ex-x-1=0，

所以当x>0时，g′(x)>0，

因为g(x)min=g(0)=0，

所以当x>0时，g(x)>0.

当00；

当x>2时，h′(x)<0，则

构造法对学生的各项能力要求较高，既要能够牢固掌握、深入把握所学知识本质，又要掌握不同题型的构造技巧，因此，教学中不仅要为学生讲解构造法相关理论，传授相关的构造技巧，又要做好构造法在解题中的应用讲解，鼓励其做好听课的总结，及时弥补学习中的不足.