虚拟CPU负载预测算法性能评估*
2022-04-26万成威
万成威,王 霞,王 猛
(北京航天飞行控制中心,北京 100094)
0 引 言
虚拟化云计算平台可实现不同云租户相对独立地共享底层基础资源,在有效满足多样化应用需求的同时,实现了底层服务器的CPU、内存、硬盘等资源的高效利用、灵活分配以及统一管理[1-2]。因此,虚拟化云平台已日渐成为各类业务系统运行的基础支撑环境[3]。为实现物理资源被多个虚拟机调用,无论软件模拟虚拟化,还是硬件辅助虚拟化,均需虚拟机监控器的参与,实现物理设备与上层多个虚拟机之间的抽象与适配。虚拟机操作系统管理和访问的系统资源,如虚拟CPU、虚拟内存、虚拟IO等,只有在虚拟CPU被调度至物理CPU时,虚拟机操作系统中的各个进程才可以运行[4]。因此,虚拟CPU调度算法直接影响着虚拟机的性能。虚拟CPU调度包含虚拟机之间的CPU调度和虚拟机内部CPU调度。这些虚拟CPU调度算法中,准确的CPU资源预测是保证算法有效性的重要前提。从系统层面看,云服务器提供商需尽可能根据虚拟机承载的业务需求动态分配或迁移虚拟机,以避免分配过多的资源形成浪费,或者因分配资源不足而影响业务运行[5-8];从虚拟机操作系统本身看,大量的虚拟机同时运行着计算密集型业务和IO密集型业务,两类业务的资源分配策略直接影响着虚拟机操作系统的综合服务性能[4,9]。因此,准确的资源需求预测是保证云平台资源调度算法有效性的重要前提,其中CPU资源预测是云平台各类资源中的核心指标。已有研究表明,在大时间尺度上,大型分布式系统中的CPU负载具有明显的自相关性、周期性等[9],故通过长期的云平台负载数据积累,使用各种数据挖掘算法,可以准确地预测云平台CPU资源的变化特性,对云平台资源的整体规划有着重要意义。然而,在小时间尺度上,各服务器或虚拟机的负载变化仍具有较强的随机性,这也为云平台虚拟机实时迁移或虚拟CPU资源实时分配带来了挑战。尤其在虚拟机操作系统环境下,可用CPU资源相对有限,且操作系统CPU调度具有很强的实时性,这就要求CPU预测及调度算法尽可能简单,且占用较小的计算、存储等资源。
考虑到虚拟机操作系统应用场景多样性所引入的随机性,本文以适用虚拟机操作系统环境的CPU预测方法为研究对象,详细评估了各种虚拟CPU资源预测算法的准确性以及算法性能随各关键参数的变化情况,为虚拟机操作系统的CPU资源调度策略设计与实现提供了研究基础。
1 CPU负载预测算法性能评估
大型云平台可以部署专用的云平台管理系统,采用负载的CPU负载预测算法,并根据定义的效益最大化原则,调整云平台资源的分配策略[10]。然而,对虚拟机操作系统而言,CPU负载预测算法需尽可能简单、高效,占用尽可能少的计算、存储等资源,不会引入较大的性能损耗和预测时延,便于实现CPU资源的快速、准确调整。本文选取了五种常见的时间序列预测算法,以CPU负载数据为研究对象,详细比较其在CPU负载预测方面的应用性能。
1.1 CPU负载数据
本文采用CloudSim[11]平台中resource/workload/20110420目录下的CPU负载数据作为研究对象,该CPU负载为PlanetLab平台上虚拟机真实的CPU负载测试数据集,可作为不同研究场景下的基准测试数据集。该目录下共包含1 054个CPU负载样本序列。本文采取无监督机器学习算法支持向量机(Support Vector Machine,SVM)将上述样本分为三类(高CPU负载序列78个,低CPU负载序列639个,混合型负载序列337个),以考察不同时间序列预测算法性能与不同CPU负载类型之间的关系。
1.2 时间序列预测算法
本文主要研究适用于虚拟机操作系统CPU调度的负载预测算法,算法需计算量小、占用存储空间小。为此,本文主要考察简单时间序列预测算法的性能,包括移动平均法[12]、加权平均法[13]、一次指数平滑法[14]、二次指数平滑法[14]、差分指数平滑法[15]等。
令各CPU负载样本为时间序列X1,X2,…,XT,对于下列各算法进行时间序列预测。
(1)平均移动法
给定移动项数N,时间序列预测值为
(1)
(2)加权平均移动法
给定移动项数N及权重系数w1,w2,…,wN,时间序列预测值为
(2)
w1+w2+…+wN=1。
(3)
(3)一次指数平滑法
给定加权系数α(0<α<1),时间序列预测值
(4)
(4)二次指数平滑法
针对一次指数平滑法的预测结果进一步指数平滑,得到的结果作为时间序列预测值,具体如下:
(5)
(6)
(7)
(8)
(9)
(5)差分指数平滑法
对一阶差分值进行指数平滑,将得到的结果作为时间序列预测值,具体如下:
ΔXt=Xt-Xt-1,
(10)
(11)
(12)
为准确评估上述各算法的预测性能,定义预测标准误差如下:
(13)
标准误差值越小,算法预测性能越优。
1.3 虚拟CPU负载预测算法性能评估
将上述各时间序列预测算法应用于1.1节所述各CPU负载序列,完成CPU负载预测性能评估。因CPU负载变化复杂,具有较大的随机性,且不同时间序列预测算法的参数差异,均会导致标准误差的计算结果发生变化,为此,定义各时间序列预测误差均值如下:
(14)
式中:Si为相同参数设置时N个不同CPU时间序列的预测标准误差。
不同算法条件下,三类CPU负载序列预测性能结果如图1所示。

(a)平均移动法
由图1可见,三类CPU负载序列的平均误差具有明显的差异,随CPU负载升高而依次增大。受CPU负载的随机性变化影响,在高CPU负载条件下,各算法预测的绝对误差也相对较大,从而产生更大的平均预测误差。
平均移动法、加权平均移动法等主要受移动项数影响,本文分别考察了两者平均预测误差随移动项数的变化情况,分别如图1(a)、(b)、(c)所示,其中加权平均移动法还受权重系数影响,一般而言,距当前时刻越近,与当前CPU负载的相关性越强,应赋予更高的权重。为简化处理,本文分别采用指数递减和线性递减方式确定权重系数。指数递减方式下,当前时刻前的N个时刻,负载权重依次为2N-1/(2N-1),2N-2/(2N-1),…,1/(2N-1);线性递减方式下,当前时刻前的N个时刻,负载权重依次为[1+2(N-1)]/N2,[1+2(N-2)]/N2,…,1。可以看到,随移动项数逐渐增大,平均移动算法和加权平均移动算法的平均预测误差均显著下降;随后,除低CPU负载序列外,其他序列的预测性能均存在不同程度的性能下降。另外,对于加权平均移动法而言,权重系数线性递减方式整体性能明显优于指数递减方式,仅在移动项数小于4时指数递减方式性能更优,但在移动项数为12时上述各种CPU负载类型及权重模式下,平均预测误差均可到达最小值。
一次指数平滑法、二次指数平滑法、差分指数平滑法等预测性能主要受加权系数α及预测序列初值影响。本文采用实际CPU负载作为各指数平滑法的预测序列初值,在此条件下详细考察其平均预测误差随加权系数的变化关系,如图1(d)、(e)、(f)所示。一次指数平滑法中,三类CPU负载序列的平均预测误差均随加权系数先递减,在加权系数为0.1时,平均预测误差达到最小,随后平均预测误差逐渐升高,甚至高于前期误差高值;而二次指数平滑法和差分指数平滑法中,三类CPU负载的平均预测误差均随加权系数增加而逐渐增大,且增大的速率明显大于一次指数平滑法。这是因为二次指数平滑法和差分指数平滑法主要为适应线性时间序列而进行了修正处理,但实际CPU负载序列仍具有较大的随机动态变化,从而产生较大的预测误差。
综上各CPU负载预测算法性能评估结果可以看到,平均移动法、线性递减加权平均移动法、一次指数平滑法具有较好的CPU负载预测性能。为此,本文进一步采用最优的参数设置,详细比较了这三种算法的预测误差,结果如图2所示。
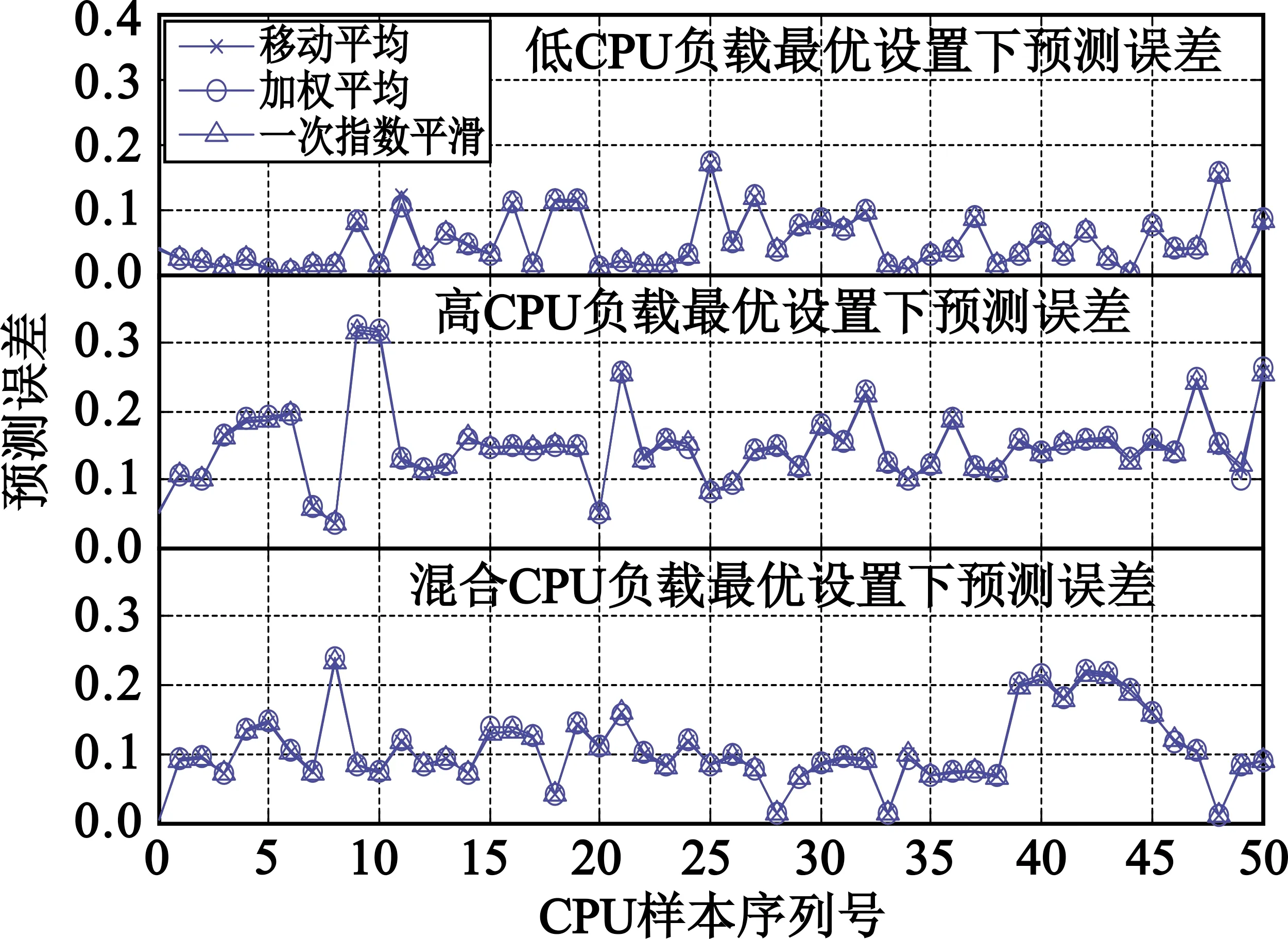
图2 最优设置下的预测误差
可以看到,最优参数设置条件下,三类算法的预测误差基本相同,整体上,一次指数平滑算法性能最优,平均移动法次之,加权平均移动法误差最大。平均移动法是一种特殊的加权平均移动法,相当于所有权重系数完全相同,形成了类似最佳接收机的效果,但仍存在某些特殊情况,如图2低CPU负载中的第11个序列(见图3)、高CPU负载中的第49个序列(见图4)。图3中整个序列中基本保持低负载,仅存在几个连续的高CPU样本;图4中高CPU负载序列垂直变化为低CPU负载序列。在上述情况下,加权平均移动法性能反而最优,而平均移动法、一次指数平滑法等由于滞后作用影响,并不能较好地适应这种迅速变化,导致预测性能较差。

图3 低CPU负载序列样本

图4 高CPU负载序列样本
1.4 一次指数平滑法的改进
一次指数平滑法计算简单,需要存储的状态参数及历史负载信息较少,且预测效果好,被广泛应用于时间序列预测领域。实际上,一次指数平滑法是对全部历史信息的加权平均,加权系数分别为α、α(1-α)、α(1-α)2……为适应CPU负载快速变化的情况,本文基于反馈控制思想对一次指数平滑法进行了改进,即当t时刻的CPU负载预测值与实际值Xt之间的差值满足
(15)
时对一次平滑法参数进行调整。考虑正常业务运行时,均会引起CPU负载升高,而一次指数平滑法得到的预测序列为CPU负载的加权平均,故当CPU负载预测值与实际值满足上述条件时,进一步降低加权系数α,以避免预测序列剧烈波动,且与实际负载序列滞后,形成更大的预测误差。本文进行上述改进后,采用三类CPU负载序列进行了验证,结果如图5所示。可以看到,在CPU负载预测值与实际值p大于0.5时,调整权重系数α至0.05,可明显降低CPU负载、混合CPU负载的预测误差,而且改进后的一次指数平滑法的预测误差随权重系数增加上升得更为缓慢。
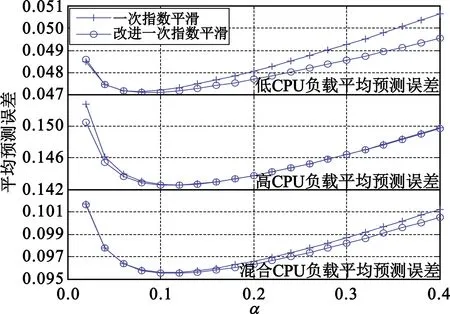
图5 改进的一次指数平滑法效果
2 结束语
准确的虚拟机操作系统CPU负载预测是实现虚拟化平台资源高效利用的基础。虚拟机操作系统环境下,可用的计算资源、存储空间等较为有限,CPU负载预测算法应尽可能简单、高效。本文基于实际的CPU负载数据,以常用的时间序列分析方法作为研究对象,详细评估了各方法在虚拟CPU负载预测领域的应用性能,结果表明,平均移动法、线性递减加权平均移动法、一次指数平滑法计算方法简单,所用存储空间极小,且具有较好的CPU负载预测性能。在此基础上,结合反馈控制思想,对一次指数平滑法进行了改进,进一步提高了其CPU负载预测性能。
后续工作主要包含以下两个方面:一是针对改进的一次指数平滑法,进一步详细评估不同条件下参数p对算法性能的影响;二是将上述方法在各虚拟化平台中实现,并在实际过程中检验其应用性能。
